Redpoll's 60
Home / 3Dプログラミング入門 / 第1章 $§$1-5
第1章 2D空間の基礎
| $§$1-1 点とベクトル | $§$1-6 回転行列 |
| $§$1-2 ベクトルによる平行移動 | $§$1-7 スケール行列 |
| $§$1-3 単位ベクトル | $§$1-8 変換行列の積 |
| $§$1-4 行列の基礎 | $§$1-9 フレームとフレームレート |
| $§$1-5 平行移動行列 | $§$1-10 オブジェクトの基本的な運動 (往復運動と回転) |
$§$1-5 平行移動行列
1-2節、1-3節において、2D空間におけるベクトルを用いた平行移動を扱った。そこではある点の移動後の位置を、ベクトル同士の加算によって求めたのであった。本節では2D空間上の点の平行移動を、その点を表す位置ベクトルと平行移動を表す行列との積によって行う。
2D空間上の点は2次元ベクトル(2Dベクトル)として表すことが可能であり、1-2節、1-3節におけるベクトルを用いた平行移動でも使われていたベクトルは2次元ベクトルであった。しかし、平行移動を行列で行う場合は2D空間上の点を、2次元ベクトルではなく次元を1次元拡張した3次元ベクトル(3Dベクトル)を用いて表す。また、その際に使う平行移動を表す行列も3次元ベクトルの次元数に合わせて$3\times3$行列を使用する。具体的には以下のように記述する。
2D空間上の点$(x, y)$\begin{pmatrix}x \\y \\ 1\end{pmatrix}2D空間上で$(a, b)$だけ平行移動させる平行移動行列(Translation Matrix)\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}2D空間上の点$(x, y)$を$(a, b)$だけ平行移動させる計算
行列による平行移動とベクトル同士の加算による平行移動は、算出される値の次元は3次元と2次元という違いはあるが本質的には同じであることが分かる(3次元ベクトルの方の$z$値を無視すれば同じ結果である)。
行列による平行移動の計算で使用された3次元化されたベクトルを同次座標(homogeneous coordinates)という。そこでは2D空間上の点$(x, y)$は2次元ベクトルではなく1次元拡張された3次元ベクトル$(x, y, 1)$として同次座標で表され、その際に使われた行列は同次座標に合わせて$2\times2$行列から$3\times3$行列へと1つ次元が拡張されたのであった。
コンピューターグラフィックスでベクトルや行列の計算が行われる際、ほとんどのケースにおいてこの同次座標が用いられる。具体的には、
2D空間では$(x, y)$を3次元ベクトル$(x, y, 1)$で表し、行列は$2\times2$ではなく$3\times3$行列を用いる。
3D空間では$(x, y, z)$を4次元ベクトル$(x, y, z, 1)$で表し、行列は$3\times3$ではなく$4\times4$行列を用いる。
同次座標に拡張する場合は、必ず1を追加する (3次元ベクトルに拡張する場合は$z$座標に、4次元ベクトルに拡張する場合は$w$座標に1を追加する)。
計算例として点$P = (-4, 1)$を、$x$方向に$6$、$y$方向に$1$、すなわち$(6, 1)$だけ平行移動させる例を以下に示す($P$の移動後の位置は$P = (2, 2)$である)。
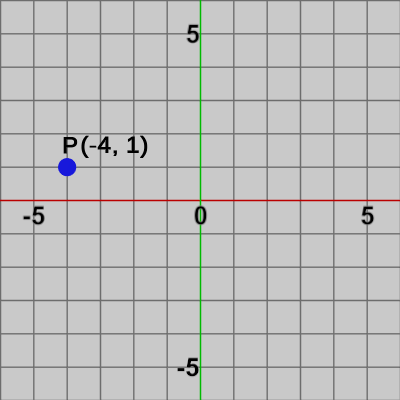
図1 点P=(-4, 1) 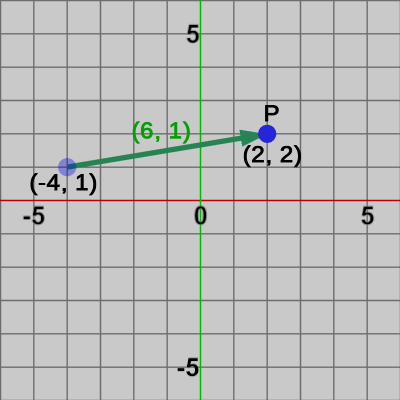
図2 点Pを(6, 1)だけ平行移動させる(P=(2, 2)に移動する)
また、1-1節でも述べたが、この講義で使用する図においては、黒色の数値は点(位置)を表し、緑色の数値はベクトルを表している。例えば、図2においては $(-4, 1)$、$(2, 2)$ は点$P$の移動前、移動後の位置を表し、$(6, 1)$ は点$P$の移動量を表すベクトルである。
最後に算出された行列は確かに$(a_1+a_2, b_1+b_2)$だけ平行移動させる行列になっている。
なお、変換行列(平行移動、回転、スケールなどの変換を表す行列)の積によってオブジェクトを動かす場合、実行される変換の順序は行列の積と同様に右から左へ進む。上の例では、まず$(a_1, b_1)$の平行移動、次に$(a_2, b_2)$の平行移動の順である。
ここでは平行移動行列の積を例にとって示したが、変換行列には次のような重要な性質がある。すなわち、変換行列の積は複数の変換を1つの行列にまとめたものになっているという性質である。
(計算例)
(1) $(-3, -4)$だけ平行移動させる行列と、$(2, 6)$だけ平行移動させる行列の積。
第1の平行移動を表す行列を$T_1$、第2の平行移動を表す行列を$T_2$とし、それらの積を$M_1$とする。
$M_1$は、まず $(-3, -4)$ の平行移動、次に $(2, 6)$ の平行移動を実行する行列である ($M_1$は結果的には$(-1, 2)$の平行移動を表す行列であるが、変換行列の積は複数の変換を1つの行列にまとめたものであるという性質をしばらくは強調する)。
(2) $(3, 0)$だけ平行移動させる行列と、$(-5, 4)$だけ平行移動させる行列、$(-2, -2)$だけ平行移動させる行列の積。
第1の平行移動を表す行列を$T_1$、第2の平行移動を表す行列を$T_2$、第3の平行移動を表す行列を$T_3$とし、それらの積を$M_2$とする。
$M_2$は、まず $(3, 0)$ の平行移動、次に $(-5, 4)$ の平行移動、さらに $(-2, -2)$ の平行移動を実行する行列である (結果的には$(-4, 2)$の平行移動を表す行列である)。
(1)、(2)の平行移動行列を初期位置が $(2, 1)$ の点に実行した結果を図3, 図4に示す。
下図においては、平行移動を表す緑色のベクトルの1つ1つが$T_1$, $T_2$, $T_3$を表し、それら全てを結合したものが$M_1$、$M_2$を表している。
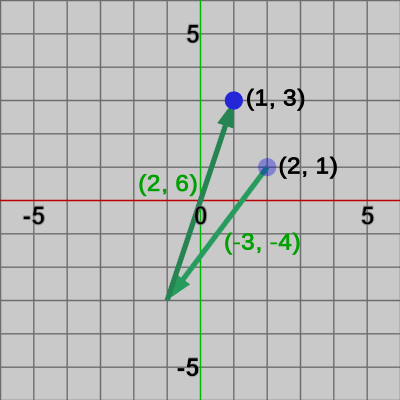
図3 (1)の平行移動 点は(1, 3)に移動する 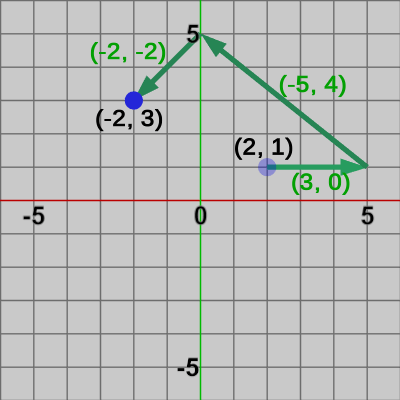
図4 (2)の平行移動 点は(-2, 3)に移動する
それぞれの移動後の位置を計算すると、
本節ではカスタムライブラリーから以下の構造体、及び メソッドを使用する。
また、第1章、第2章のプログラムで使われるオブジェクトはカスタムライブラリーのTHObject2Dクラスのインスタンスであり、オブジェクトに対して変換行列を実行するには、THObject2Dクラスの以下のメソッドを使用する。
例えば、$(10, 20)$の平行移動を行う行列を取得し、オブジェクトに その平行移動行列を実行するためには、プログラムに以下のように記述する。
では、オブジェクトに変換行列を実行する具体的な例を1つ見てみよう。
今まで2D空間の点は全て円形状で表されていた。ここでは図5に示される四角形のオブジェクトSquareが2D空間の点を表すものとする。このオブジェクトに上記のメソッドを使って平行移動行列をセットし、オブジェクトに平行移動を実行してみよう。
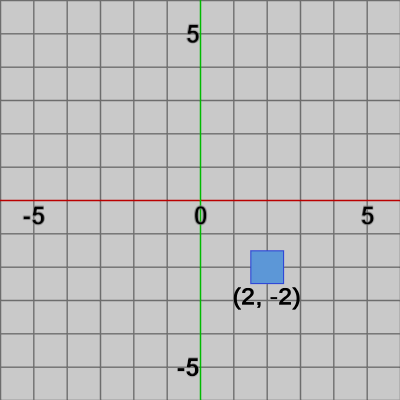
図5 Square 初期位置(2, -2) 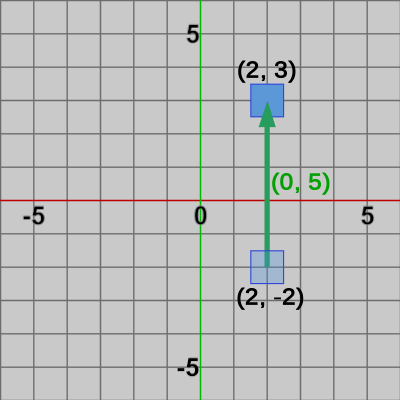
図6 Squareに(0, 5)の平行移動を実行 ( (2, 3)に移動する)
Squareが何の変換も受けていない初期の状態での位置は $(2, -2)$である(図5)。
この状態のSquareに対し、y軸方向に$5$の平行移動、すなわち $(0, 5)$の平行移動を実行する。
この平行移動を表す行列を$T$とすれば、Squareの初期位置は $(-2, 2)$であるから、移動後の位置は次のように計算される。\[T\begin{pmatrix}2 \\-2 \\ 1\end{pmatrix}=\begin{pmatrix}1 &0 &0 \\0 &1 &5 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\-2 \\ 1\end{pmatrix}=\begin{pmatrix}2 \\3 \\ 1\end{pmatrix}\]この平行移動を実行するプログラムを以下に示す。
このプログラムを実行すると、図6に示されるように Squareはy軸方向に$5$だけ平行移動し、結果的に $(2, 3)$へ移ることになる。
では最後に、本節で述べた内容に関するプログラムを作成する。
(1) まず $(-3, -4)$の平行移動、次に $(2, 6)$の平行移動を実行。
(2) まず $(3, 0)$の平行移動、次に $(-5, 4)$の平行移動、最後に $(-2, -2)$の平行移動を実行。
これらの平行移動はいずれも、初期位置を $(2, 1)$として実行するものとする。
[Code1] (実行結果 図7)
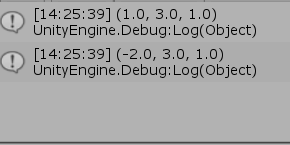
図7 Code1 実行結果 1行目の (2, 1, 1) は、平行移動行列との積を可能にするために、平行移動の開始位置 (2, 1)を同次座標で表したものである。
図7に表示されている結果は同次座標であるが、それらは上での計算結果と一致している。
6行目、14行目は行列の積の記述であるが、何度か述べたように行列の積は右から左へ進む(詳しくは 列優先行列の場合 ; 3-8節参照)。したがって、実行される変換の順序も右から左の順で実行される。例えば、6行目の積は T1による平行移動、T2による平行移動の順で変換が行われることを意味する。具体的には、まず $(-3, -4)$の平行移動、次に $(2, 6)$の平行移動という順で実行されるが、M1の内容は、この2つの平行移動をまとめた $(-1, 2)$の平行移動というものになる。
7行目、15行目は Vector3インスタンスと THMatrix3x3インスタンスとの積であるが、ベクトルと行列の積をこのように直接的に記述することが可能である。この積の結果は、Vector3インスタンスとして返される。
なお、1-4節でも見たように、$3\times3$行列と3次元ベクトルとの積は3次元ベクトルである。そして、そこで見たように行列とベクトルの積の場合は、行列を積の左側、ベクトルを積の右側に記述する。例えば、上のプログラムの7行目では、THMatrix3x3型の M1が積の左側、Vector3型の Pが積の右側に記述されている。
図5に示されるように、Squareの初期位置は $(2, -2)$であるが、ここでは、初期値から まず$(-6, 3)$だけ平行移動させ、次に$(4, 4)$だけ平行移動させる。
第1の平行移動行列を$T_1$、第2の平行移動行列を$T_2$とすると、\[T_1 =\begin{pmatrix}1 &0 &-6 \\0 &1 &3 \\ 0 &0 &1\end{pmatrix}\qquad T_2 =\begin{pmatrix}1 &0 &4 \\0 &1 &4 \\ 0 &0 &1\end{pmatrix}\]である。
この2つの平行移動を合成する。それは上記の計算例で見たように、2つの平行移動行列を実行順に掛ければよい (積を$M$とする)。
すなわち、Squareに2つの平行移動行列を実行すると、最終的には始めの位置から $(-2, 7)$ だけ平行移動することになる。したがって、Squareの最終的な位置は次のように求められる (以下の $\boldsymbol{\mathsf{p}}$ は Squareの初期位置 $(2, -2)$ を表す同次座標化したベクトルである。$M\boldsymbol{\mathsf{p}}$は、行列$M$とベクトル$\boldsymbol{\mathsf{p}}$の積を意味する)。
では以上の処理をプログラムに記述しよう。
[Code2] (実行結果 図9)
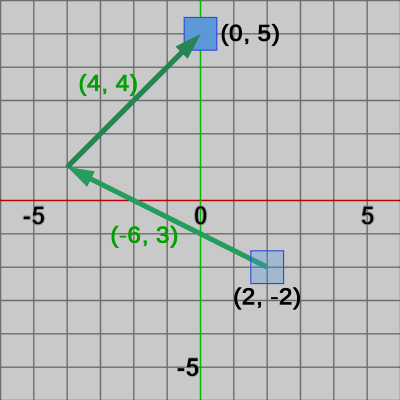
図8 Squareに実行される2つの平行移動を可視化した図 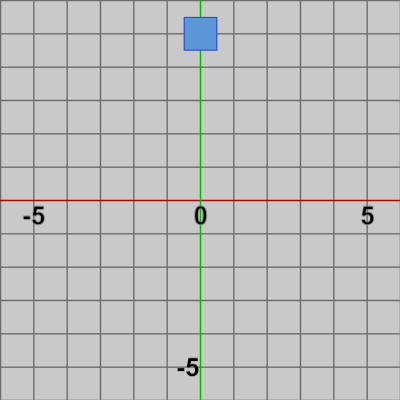
図9 Code2 実行結果
プログラムで使われている変数は上記の文章中のものと同じであるから特に解説は必要ないであろう。図8は、Squareに実行される2つの平行移動行列$T_1$、$T_2$を可視化したものである。まず $(-6, 3)$の平行移動($T_1$)、次に $(4, 4)$の平行移動($T_2$) の順で行われる様子を示している。プログラムの実行結果は図9である。
3つの平行移動は次の順序で実行する。
最初に $(1,\ 5)$ の平行移動、次に $(-4,\ 1)$ の平行移動、最後に $(-1, -5)$ の平行移動の順で実行する。
第1の平行移動行列を $T_1$、第2の平行移動行列を $T_2$、第3の平行移動行列を $T_3$ とすれば、
となるが、これは $T_1$、$T_2$、$T_3$の順序で平行移動を行うと最終的には、$(-4,\ 1)$だけの平行移動が実行されることを意味している。
したがって、Squareの初期位置 $(2, -2)$ の同次座標を表すベクトルを$\boldsymbol{\mathsf{p}}$とすれば、今回の3つの平行移動を実行した後の$\boldsymbol{\mathsf{p}}$の位置は以下のように計算される。
実際のプログラムは次のとおり。
[Code3] (実行結果 図11)
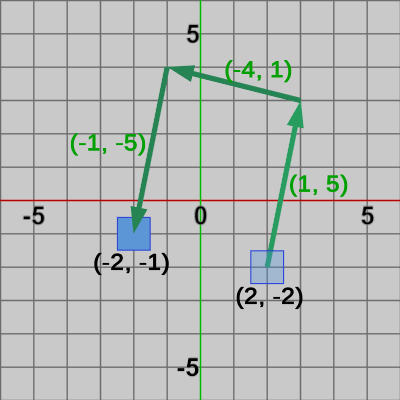
図10 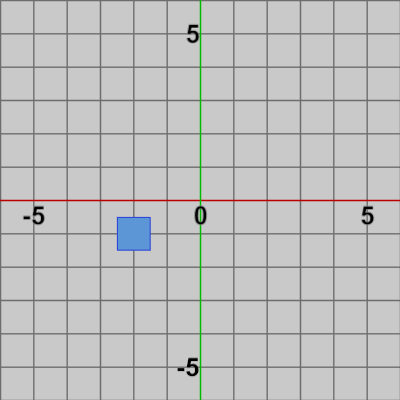
図11 Code3 実行結果
図10は、Squareに実行される2つの平行移動行列$T_1$、$T_2$、$T_3$を可視化したものである。まず $(1, 5)$の平行移動($T_1$)、次に $(-4, 1)$の平行移動($T_2$)、最後に $(-1, -5)$の平行移動($T_3$)の順で行われる様子を示している。プログラムの実行結果は図11である。
先ほども少し触れたが、第5章まではオブジェクトの運動は基本的に行列を通して実行する。Unityの標準機能による記述は第6章のQuaternionのあたりから始めることになる。
行列はベクトルと並んでコンピューターグラフィックスにおける最も重要な概念の1つである。オブジェクトに対してさまざまな変換を行うプログラムを作成する際にも、行列を用いる方が直観的であるし、なぜ現在オブジェクトがそういった状態になっているのか、あるいはオブジェクトをそういった状態にするためにはどのような変換を実行すればよいのか、なども行列を利用する方がわかりやすいのである。特に第4章、第5章において解説されるいくつかの重要な事実を理解するためには、行列の基本的な部分を把握しておくことが必要になるのである。
A) 点の平行移動
まず始めに、一つ重要な変更をしておく必要がある。2D空間上の点は2次元ベクトル(2Dベクトル)として表すことが可能であり、1-2節、1-3節におけるベクトルを用いた平行移動でも使われていたベクトルは2次元ベクトルであった。しかし、平行移動を行列で行う場合は2D空間上の点を、2次元ベクトルではなく次元を1次元拡張した3次元ベクトル(3Dベクトル)を用いて表す。また、その際に使う平行移動を表す行列も3次元ベクトルの次元数に合わせて$3\times3$行列を使用する。具体的には以下のように記述する。
2D空間上の点$(x, y)$\begin{pmatrix}x \\y \\ 1\end{pmatrix}2D空間上で$(a, b)$だけ平行移動させる平行移動行列(Translation Matrix)\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}2D空間上の点$(x, y)$を$(a, b)$だけ平行移動させる計算
\begin{align*}\begin{pmatrix}1 &0 &a \\0 &1 &b \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}x \\y \\ 1\end{pmatrix}=\begin{pmatrix}1\cdot x + 0\cdot y + a\cdot 1 \\0\cdot x + 1\cdot y + b\cdot 1 \\ 0\cdot x + 0\cdot y + 1\cdot 1\end{pmatrix}=\begin{pmatrix}x + a \\y + b \\ 1\end{pmatrix}\end{align*}
同じことをベクトル同士の加算によって行った場合\begin{align*}\begin{pmatrix}x \\y \end{pmatrix}+\begin{pmatrix}a \\b \end{pmatrix}=\begin{pmatrix}x + a \\y + b\end{pmatrix}\end{align*}行列による平行移動とベクトル同士の加算による平行移動は、算出される値の次元は3次元と2次元という違いはあるが本質的には同じであることが分かる(3次元ベクトルの方の$z$値を無視すれば同じ結果である)。
行列による平行移動の計算で使用された3次元化されたベクトルを同次座標(homogeneous coordinates)という。そこでは2D空間上の点$(x, y)$は2次元ベクトルではなく1次元拡張された3次元ベクトル$(x, y, 1)$として同次座標で表され、その際に使われた行列は同次座標に合わせて$2\times2$行列から$3\times3$行列へと1つ次元が拡張されたのであった。
コンピューターグラフィックスでベクトルや行列の計算が行われる際、ほとんどのケースにおいてこの同次座標が用いられる。具体的には、
2D空間では$(x, y)$を3次元ベクトル$(x, y, 1)$で表し、行列は$2\times2$ではなく$3\times3$行列を用いる。
3D空間では$(x, y, z)$を4次元ベクトル$(x, y, z, 1)$で表し、行列は$3\times3$ではなく$4\times4$行列を用いる。
同次座標に拡張する場合は、必ず1を追加する (3次元ベクトルに拡張する場合は$z$座標に、4次元ベクトルに拡張する場合は$w$座標に1を追加する)。
計算例として点$P = (-4, 1)$を、$x$方向に$6$、$y$方向に$1$、すなわち$(6, 1)$だけ平行移動させる例を以下に示す($P$の移動後の位置は$P = (2, 2)$である)。


\begin{align*}\begin{pmatrix}1 &0 &6 \\0 &1 &1 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}-4 \\1 \\ 1\end{pmatrix}=\begin{pmatrix}1\cdot(-4) + 0\cdot1 + 6\cdot 1 \\0\cdot(-4) + 1\cdot1 + 1\cdot 1 \\ 0\cdot(-4) + 0 + 1\cdot 1\end{pmatrix}=\begin{pmatrix}-4 + 6 \\1 + 1 \\ 1\end{pmatrix}=\begin{pmatrix}2 \\2 \\ 1\end{pmatrix}\end{align*}
算出される値は同次座標の$(2, 2, 1)$であるが、$z$値を無視すれば確かに計算結果は移動後の位置になっていることが分かる。また、1-1節でも述べたが、この講義で使用する図においては、黒色の数値は点(位置)を表し、緑色の数値はベクトルを表している。例えば、図2においては $(-4, 1)$、$(2, 2)$ は点$P$の移動前、移動後の位置を表し、$(6, 1)$ は点$P$の移動量を表すベクトルである。
B) 平行移動行列の積
複数の平行移動の合成は、それらの平行移動を表す行列の積によって表される。例えば、2つの平行移動の合成は それらの平行移動を表す2つの平行移動行列の積によって表される。具体的には、$(a_1, b_1)$だけ平行移動させる行列と、$(a_2, b_2)$だけ平行移動させる行列の積は $(a_1+a_2, b_1+b_2)$だけ平行移動させる行列になる。以下にそれを示そう。\begin{align*}\begin{pmatrix}1 &0 &a_2 \\0 &1 &b_2 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &a_1 \\0 &1 &b_1 \\ 0 &0 &1\end{pmatrix}&=\begin{pmatrix}1\cdot 1 + 0\cdot 0 + a_2\cdot 0 &1\cdot 0 + 0\cdot 1 + a_2\cdot 0 &1\cdot a_1 + 0\cdot b_1 + a_2\cdot 1\\0\cdot 1 + 1\cdot 0 + b_2\cdot 0 &0\cdot 0 + 1\cdot 1 + b_2\cdot 0 &0\cdot a_1 + 1\cdot b_1 + b_2\cdot 1\\0\cdot 1 + 0\cdot 0 + 1\cdot 0 &0\cdot 0 + 0\cdot 1 + 1\cdot 0 &0\cdot a_1 + 0\cdot b_1 + 1\cdot 1\end{pmatrix}\\&=\begin{pmatrix}1+0+0 &0+0+0 &a_1+0+a_2 \\0+0+0 &0+1+0 &0+b_1+b_2 \\ 0+0+0 &0+0+0 &0+0+1\end{pmatrix}\\&=\begin{pmatrix}1 &0 &a_1+a_2 \\0 &1 &b_1+b_2 \\ 0 &0 &1\end{pmatrix}\end{align*}
最後に算出された行列は確かに$(a_1+a_2, b_1+b_2)$だけ平行移動させる行列になっている。
なお、変換行列(平行移動、回転、スケールなどの変換を表す行列)の積によってオブジェクトを動かす場合、実行される変換の順序は行列の積と同様に右から左へ進む。上の例では、まず$(a_1, b_1)$の平行移動、次に$(a_2, b_2)$の平行移動の順である。
ここでは平行移動行列の積を例にとって示したが、変換行列には次のような重要な性質がある。すなわち、変換行列の積は複数の変換を1つの行列にまとめたものになっているという性質である。
(計算例)
(1) $(-3, -4)$だけ平行移動させる行列と、$(2, 6)$だけ平行移動させる行列の積。
第1の平行移動を表す行列を$T_1$、第2の平行移動を表す行列を$T_2$とし、それらの積を$M_1$とする。
\[T_2T_1 = \begin{pmatrix}1 &0 &2 \\0 &1 &6 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &-3 \\0 &1 &-4 \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-3+2 \\0 &1 &-4+6 \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-1 \\0 &1 &2 \\ 0 &0 &1\end{pmatrix}= M_1\]
$M_1$は、まず $(-3, -4)$ の平行移動、次に $(2, 6)$ の平行移動を実行する行列である ($M_1$は結果的には$(-1, 2)$の平行移動を表す行列であるが、変換行列の積は複数の変換を1つの行列にまとめたものであるという性質をしばらくは強調する)。
(2) $(3, 0)$だけ平行移動させる行列と、$(-5, 4)$だけ平行移動させる行列、$(-2, -2)$だけ平行移動させる行列の積。
第1の平行移動を表す行列を$T_1$、第2の平行移動を表す行列を$T_2$、第3の平行移動を表す行列を$T_3$とし、それらの積を$M_2$とする。
\[T_3T_2T_1 = \begin{pmatrix}1 &0 &-2 \\0 &1 &-2 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &-5 \\0 &1 & 4 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 & 3 \\0 &1 & 0 \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &3+(-5)+(-2) \\0 &1 &0+4+(-2) \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-4 \\0 &1 &2 \\ 0 &0 &1\end{pmatrix}= M_2\]
$M_2$は、まず $(3, 0)$ の平行移動、次に $(-5, 4)$ の平行移動、さらに $(-2, -2)$ の平行移動を実行する行列である (結果的には$(-4, 2)$の平行移動を表す行列である)。
(1)、(2)の平行移動行列を初期位置が $(2, 1)$ の点に実行した結果を図3, 図4に示す。
下図においては、平行移動を表す緑色のベクトルの1つ1つが$T_1$, $T_2$, $T_3$を表し、それら全てを結合したものが$M_1$、$M_2$を表している。


それぞれの移動後の位置を計算すると、
\begin{align*}\begin{pmatrix}1 &0 &-1 \\0 &1 &2 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\1 \\1\end{pmatrix}&=\begin{pmatrix}2+(-1)\\1+2\\ 1\end{pmatrix}=\begin{pmatrix}1\\3\\1\end{pmatrix}\\\\\begin{pmatrix}1 &0 &-4 \\0 &1 &2 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\1 \\1\end{pmatrix}&=\begin{pmatrix}2+(-4)\\1+2\\ 1\end{pmatrix}=\begin{pmatrix}-2\\3\\1\end{pmatrix}\end{align*}
となる(移動後の位置は$z$値を取り除いた$(1, 3)$、$(-2, 3)$である)。C) オブジェクトに平行移動行列を実行する
UnityのC#スクリプトの標準機能を用いてオブジェクトを動かす場合は、Transformクラスを経由する。しかし、前節でも少し触れたがTransformクラスには行列を扱うメソッドがないため、行列を使ってオブジェクトを動かす場合には、講義用に用意したカスタムライブラリーの機能を使う必要がある。本節ではカスタムライブラリーから以下の構造体、及び メソッドを使用する。
THMatrix3x3
: $3\times3$行列用の構造体。TH2DMath.GetTranslation3x3(float x, float y)
: 2D空間において $(x, y)$の平行移動を実行する平行移動行列を取得するための TH2DMathクラスの staticメソッドで、戻り値は THMatrix3x3型のインスタンス (TH2DMathクラスはカスタムライブラリのユーティリティクラス) 。また、第1章、第2章のプログラムで使われるオブジェクトはカスタムライブラリーのTHObject2Dクラスのインスタンスであり、オブジェクトに対して変換行列を実行するには、THObject2Dクラスの以下のメソッドを使用する。
SetMatrix(THMatrix3x3 m)
: 2D空間のオブジェクトに対して、引数で指定された変換行列を実行する。例えば、$(10, 20)$の平行移動を行う行列を取得し、オブジェクトに その平行移動行列を実行するためには、プログラムに以下のように記述する。
THMatrix3x3 T = TH2DMath.GetTranslation3x3(10, 20); Obj.SetMatrix(T);
では、オブジェクトに変換行列を実行する具体的な例を1つ見てみよう。
今まで2D空間の点は全て円形状で表されていた。ここでは図5に示される四角形のオブジェクトSquareが2D空間の点を表すものとする。このオブジェクトに上記のメソッドを使って平行移動行列をセットし、オブジェクトに平行移動を実行してみよう。


Squareが何の変換も受けていない初期の状態での位置は $(2, -2)$である(図5)。
この状態のSquareに対し、y軸方向に$5$の平行移動、すなわち $(0, 5)$の平行移動を実行する。
この平行移動を表す行列を$T$とすれば、Squareの初期位置は $(-2, 2)$であるから、移動後の位置は次のように計算される。\[T\begin{pmatrix}2 \\-2 \\ 1\end{pmatrix}=\begin{pmatrix}1 &0 &0 \\0 &1 &5 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\-2 \\ 1\end{pmatrix}=\begin{pmatrix}2 \\3 \\ 1\end{pmatrix}\]この平行移動を実行するプログラムを以下に示す。
THMatrix3x3 T = TH2DMath.GetTranslation3x3(0, 5); Square.SetMatrix(T);
このプログラムを実行すると、図6に示されるように Squareはy軸方向に$5$だけ平行移動し、結果的に $(2, 3)$へ移ることになる。
では最後に、本節で述べた内容に関するプログラムを作成する。
# Code1
本節の中程で見た 計算例 をここではプログラムで実装する。(1) まず $(-3, -4)$の平行移動、次に $(2, 6)$の平行移動を実行。
(2) まず $(3, 0)$の平行移動、次に $(-5, 4)$の平行移動、最後に $(-2, -2)$の平行移動を実行。
これらの平行移動はいずれも、初期位置を $(2, 1)$として実行するものとする。
[Code1] (実行結果 図7)
Vector3 P = new Vector3(2, 1, 1); // (2, 1) の同次座標 // (1) THMatrix3x3 T1 = TH2DMath.GetTranslation3x3(-3, -4); THMatrix3x3 T2 = TH2DMath.GetTranslation3x3(2, 6); THMatrix3x3 M1 = T2 * T1; Vector3 P1 = M1 * P; Debug.Log(P1); // (2) T1 = TH2DMath.GetTranslation3x3(3, 0); T2 = TH2DMath.GetTranslation3x3(-5, 4); THMatrix3x3 T3 = TH2DMath.GetTranslation3x3(-2, -2); THMatrix3x3 M2 = T3 * T2 * T1; Vector3 P2 = M2 * P; Debug.Log(P2);

図7に表示されている結果は同次座標であるが、それらは上での計算結果と一致している。
6行目、14行目は行列の積の記述であるが、何度か述べたように行列の積は右から左へ進む(詳しくは 列優先行列の場合 ; 3-8節参照)。したがって、実行される変換の順序も右から左の順で実行される。例えば、6行目の積は T1による平行移動、T2による平行移動の順で変換が行われることを意味する。具体的には、まず $(-3, -4)$の平行移動、次に $(2, 6)$の平行移動という順で実行されるが、M1の内容は、この2つの平行移動をまとめた $(-1, 2)$の平行移動というものになる。
7行目、15行目は Vector3インスタンスと THMatrix3x3インスタンスとの積であるが、ベクトルと行列の積をこのように直接的に記述することが可能である。この積の結果は、Vector3インスタンスとして返される。
なお、1-4節でも見たように、$3\times3$行列と3次元ベクトルとの積は3次元ベクトルである。そして、そこで見たように行列とベクトルの積の場合は、行列を積の左側、ベクトルを積の右側に記述する。例えば、上のプログラムの7行目では、THMatrix3x3型の M1が積の左側、Vector3型の Pが積の右側に記述されている。
# Code2
次に、上で使用したオブジェクトSquare(図5)に対して平行移動を実行するプログラムを作成する。図5に示されるように、Squareの初期位置は $(2, -2)$であるが、ここでは、初期値から まず$(-6, 3)$だけ平行移動させ、次に$(4, 4)$だけ平行移動させる。
第1の平行移動行列を$T_1$、第2の平行移動行列を$T_2$とすると、\[T_1 =\begin{pmatrix}1 &0 &-6 \\0 &1 &3 \\ 0 &0 &1\end{pmatrix}\qquad T_2 =\begin{pmatrix}1 &0 &4 \\0 &1 &4 \\ 0 &0 &1\end{pmatrix}\]である。
この2つの平行移動を合成する。それは上記の計算例で見たように、2つの平行移動行列を実行順に掛ければよい (積を$M$とする)。
\begin{align*}T_2T_1 =\begin{pmatrix}1 &0 &4 \\0 &1 &4 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &-6 \\0 &1 &3 \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-6+4 \\0 &1 &3+4 \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-2 \\0 &1 &7 \\ 0 &0 &1\end{pmatrix}=M\end{align*}
$M$は、まず $(-6, 3)$ 平行移動させ、次に $(4, 4)$ 平行移動させる行列である (結果的には $(-2, 7)$ の平行移動を表す行列である)。すなわち、Squareに2つの平行移動行列を実行すると、最終的には始めの位置から $(-2, 7)$ だけ平行移動することになる。したがって、Squareの最終的な位置は次のように求められる (以下の $\boldsymbol{\mathsf{p}}$ は Squareの初期位置 $(2, -2)$ を表す同次座標化したベクトルである。$M\boldsymbol{\mathsf{p}}$は、行列$M$とベクトル$\boldsymbol{\mathsf{p}}$の積を意味する)。
\begin{align*}(T_2T_1)\boldsymbol{\mathsf{p}} = M\boldsymbol{\mathsf{p}} =\begin{pmatrix}1 &0 &-2 \\0 &1 &7 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\-2\\1\end{pmatrix}=\begin{pmatrix}2 + (-2) \\-2 + 7\\1\end{pmatrix}=\begin{pmatrix}0 \\5 \\1\end{pmatrix}\end{align*}
では以上の処理をプログラムに記述しよう。
[Code2] (実行結果 図9)
THMatrix3x3 T1 = TH2DMath.GetTranslation3x3(-6, 3); THMatrix3x3 T2 = TH2DMath.GetTranslation3x3(4, 4); THMatrix3x3 M = T2 * T1; Square.SetMatrix(M);


プログラムで使われている変数は上記の文章中のものと同じであるから特に解説は必要ないであろう。図8は、Squareに実行される2つの平行移動行列$T_1$、$T_2$を可視化したものである。まず $(-6, 3)$の平行移動($T_1$)、次に $(4, 4)$の平行移動($T_2$) の順で行われる様子を示している。プログラムの実行結果は図9である。
# Code3
続いて、Square(図5)に対して平行移動を実行するが、ここでは3つの平行移動を合成したものを Squareに実行する。しかし、内容としては Code2と同じである。3つの平行移動は次の順序で実行する。
最初に $(1,\ 5)$ の平行移動、次に $(-4,\ 1)$ の平行移動、最後に $(-1, -5)$ の平行移動の順で実行する。
第1の平行移動行列を $T_1$、第2の平行移動行列を $T_2$、第3の平行移動行列を $T_3$ とすれば、
\[T_1 =\begin{pmatrix}1 &0 &1 \\0 &1 &5 \\ 0 &0 &1\end{pmatrix}\qquad T_2 =\begin{pmatrix}1 &0 &-4 \\0 &1 &1 \\ 0 &0 &1\end{pmatrix}\qquad T_3 =\begin{pmatrix}1 &0 &-1 \\0 &1 &-5 \\ 0 &0 &1\end{pmatrix}\]
である。さらに、この3つの平行移動行列 $T_1$、$T_2$、$T_3$ の積$M = T_3T_2T_1$ を求めると、\begin{align*}T_3T_2T_1 &=\begin{pmatrix}1 &0 &-1 \\0 &1 &-5 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &-4 \\0 &1 &1 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}1 &0 &1 \\0 &1 &5 \\ 0 &0 &1\end{pmatrix}\\\\&=\begin{pmatrix}1 &0 &1+(-4)+(-1) \\0 &1 &5+1+(-5) \\ 0 &0 &1\end{pmatrix}=\begin{pmatrix}1 &0 &-4 \\0 &1 &1 \\ 0 &0 &1\end{pmatrix}=M\end{align*}
となるが、これは $T_1$、$T_2$、$T_3$の順序で平行移動を行うと最終的には、$(-4,\ 1)$だけの平行移動が実行されることを意味している。
したがって、Squareの初期位置 $(2, -2)$ の同次座標を表すベクトルを$\boldsymbol{\mathsf{p}}$とすれば、今回の3つの平行移動を実行した後の$\boldsymbol{\mathsf{p}}$の位置は以下のように計算される。
\begin{align*}(T_3T_2T_1)\boldsymbol{\mathsf{p}} = M\boldsymbol{\mathsf{p}} =\begin{pmatrix}1 &0 &-4 \\0 &1 &1 \\ 0 &0 &1\end{pmatrix}\begin{pmatrix}2 \\-2\\1\end{pmatrix}=\begin{pmatrix}2 + (-4) \\-2 + 1\\1\end{pmatrix}=\begin{pmatrix}-2 \\-1 \\1\end{pmatrix}\end{align*}
実際のプログラムは次のとおり。
[Code3] (実行結果 図11)
THMatrix3x3 T1 = TH2DMath.GetTranslation3x3(1, 5); THMatrix3x3 T2 = TH2DMath.GetTranslation3x3(-4, 1); THMatrix3x3 T3 = TH2DMath.GetTranslation3x3(-1, -5); THMatrix3x3 M = T3 * T2 * T1; Square.SetMatrix(M);


図10は、Squareに実行される2つの平行移動行列$T_1$、$T_2$、$T_3$を可視化したものである。まず $(1, 5)$の平行移動($T_1$)、次に $(-4, 1)$の平行移動($T_2$)、最後に $(-1, -5)$の平行移動($T_3$)の順で行われる様子を示している。プログラムの実行結果は図11である。
先ほども少し触れたが、第5章まではオブジェクトの運動は基本的に行列を通して実行する。Unityの標準機能による記述は第6章のQuaternionのあたりから始めることになる。
行列はベクトルと並んでコンピューターグラフィックスにおける最も重要な概念の1つである。オブジェクトに対してさまざまな変換を行うプログラムを作成する際にも、行列を用いる方が直観的であるし、なぜ現在オブジェクトがそういった状態になっているのか、あるいはオブジェクトをそういった状態にするためにはどのような変換を実行すればよいのか、なども行列を利用する方がわかりやすいのである。特に第4章、第5章において解説されるいくつかの重要な事実を理解するためには、行列の基本的な部分を把握しておくことが必要になるのである。
© 2020-2025 Redpoll's 60 (All rights reserved)