Redpoll's 60
Home / 3Dプログラミング入門 / 第14章 $§$14-3
第14章 数学的事柄についての補足
| $§$14-1 外積の導出 | $§$14-8 球面線形補間の実装 |
| $§$14-2 TRS分解における回転行列 | $§$14-9 ベクトルを一致させる回転 |
| $§$14-3 三角形の重心座標 (barycentric coordinates) | $§$14-10 Quaternion、回転行列、オイラー角の相互変換 |
| $§$14-4 Möller-Trumbore algorithm (レイ vs 三角形) | $§$14-11 二線分間の最短距離 |
| $§$14-5 法線ベクトルの変換 | $§$14-12 「直方体 vs 直方体」における分離軸 |
| $§$14-6 Quaternion 基礎 | $§$14-13 2D空間における特異値分解 |
| $§$14-7 Quaternionによる回転の表現 |
$§$14-3 三角形の重心座標 (barycentric coordinates)
3次元空間内の同一平面上に4点 $A$、$B$、$C$、$P$ があるとする。$P$ が3つの実数 $s$、$t$、$u$ を用いて以下の式で表されるとき\[ P = \frac{sA + tB + uC}{s+t+u} \tag{$B_1$} \]$(s,t,u)$ を $P$ の重心座標 (barycentric coordinates)という。
この式の右辺の分母を払って $(s + t + u)P = sA + tB + uC$ とし、左辺を右辺に移すと、\[s(A - P) + t(B - P) + u(C - P) = \boldsymbol{0}\]すなわち、\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \tag{$B_2$} \]の形になるが、この式は単に最初の式を書き換えただけであり、やはり $(s,\ t,\ u)$ が $P$ の重心座標であることを表す式である。
定義からわかるように重心座標は一意的には決まらない。例えば3つの数 $d$、$e$、$f$ の比が $s:t:u$ であるならば $(d, e, f)$ も $(2d,\ 2e,\ 2f)$ も $P$ の重心座標である。ただし本節では簡単のため $(s, t, u)$ が重心座標であるとき各成分を'正規化'された値、具体的には $\underline{s + t + u = 1}$ であるとする。
$\triangle{ABC}$ に関して点 $P$ を重心座標で表す場合、$P$ が $\triangle{ABC}$ の内側であっても外側であっても重心座標は定義されるが、本節においては点 $P$ が $\triangle{ABC}$ に含まれる場合(内部あるいは周上にある場合)のみを対象とする。後に示すが、この場合には $P$ の重心座標の各成分はいずれも $0$ 以上の値であり($s, t, u \geq 0$)、$\triangle{ABC}$ の面積を $s+t+u$ と同じく $1$ とすれば重心座標 $(s, t, u)$ は $\triangle{PBC}$、$\triangle{PCA}$、$\triangle{PAB}$ の面積に等しくなるのである。
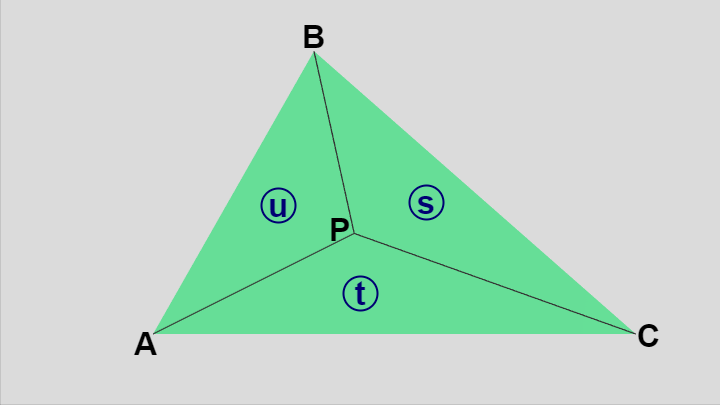
図1 点 $P$ の重心座標 $(s,t,u)$ ($\triangle{ABC}$ の面積及び $s+t+u$ の値が同じであれば $s$、$t$、$u$ は $\triangle{PBC}$、$\triangle{PCA}$、$\triangle{PAB}$ の面積に等しい)
点 $P$ が冒頭の式 $(B_1)$ あるいは $(B_2)$ の形で表されるとき、$(s,\ t,\ u)$ を「$\triangle{ABC}$ に関する点 $P$ の重心座標」と呼ぶことにすれば、$(s,\ t,\ u)$ が $\triangle{ABC}$ に関する点 $P$ の重心座標であり、さらに $s, t, u \geq 0$ であることは次の式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]として表すことができる。
先程「$(s,\ t,\ u)$ が重心座標ならば $s+t+u = 1$ とする」と定めたが、(1) が成り立つとき $(s,\ t,\ u)$ は重心座標であるから、(1) が成り立つならば $\underline{s+t+u = 1}$ であることには注意しよう。
(重心座標は必ずしも三角形のみに定義されるものではなく、より一般の形で定義される。また本節では重心座標の各成分が $0$ 以上になる場合しか扱わないが、一般の状況においては重心座標の各成分はプラスにもマイナスにもなり得る。なお解説中の三角形についてはその各頂点が時計周り(clockwise-order)であることが前提である)
まず三角形の重心座標に関する基本的な命題を証明する。
(証明) まず点 $P$ が $\triangle{ABC}$ に含まれ、3つの三角形の面積比が $|\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u$ であるとすれば、$0$ でない適当な実数 $k$ によってその3つの三角形の面積を $ks$、$kt$、$ku$ と置くことができる。$s$、$t$、$u$ はこの時点ではプラスかマイナスかはわかっていないが、面積比が $s:t:u$ であることからいずれも符号は同じであることに注意しよう ($s, t, u \geq 0$ あるいは $s, t, u < 0$)。
上図1から $2ks = |\overrightarrow{PC}\times \overrightarrow{PB}|$、$2kt = |\overrightarrow{PA}\times \overrightarrow{PC}|$、$2ku = |\overrightarrow{PB}\times \overrightarrow{PA}|$ である (XY平面上に置かれているから、この3つの外積はいずれも z軸プラス方向を向く)。
ここで $\overrightarrow{PA} = (a_x,\ a_y)$、$\overrightarrow{PB} = (b_x,\ b_y)$、$\overrightarrow{PC} = (c_x,\ c_y)$ と置き、以下の式を計算すると
であるから、$s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0}$、すなわち冒頭の $(B_2)$ が成り立つ。$(B_2)$ が成り立つならば $s$、$t$、$u$ は重心座標であり、したがって上の取り決めにより $s+t+u = 1$ である。$s$、$t$、$u$ はいずれもプラスであるか、マイナスであるかのどちらかであったが、$s+t+u=1$ によりいずれもプラスであることがわかる。以上から (1) が成り立つことが示された。
逆に (1) が成り立つとする。
$\overrightarrow{PA} = \overrightarrow{PC} + \overrightarrow{CA}$、$\overrightarrow{PB} = \overrightarrow{PC} + \overrightarrow{CB}$ であるから (1) より、\begin{align*}&s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} \\\\=\ &s(\overrightarrow{PC} + \overrightarrow{CA}) + t(\overrightarrow{PC} + \overrightarrow{CB}) + u\overrightarrow{PC} \\\\=\ &s\overrightarrow{CA} + t\overrightarrow{CB} + (s+t+u)\overrightarrow{PC} \\\\=\ &s\overrightarrow{CA} + t\overrightarrow{CB} + \overrightarrow{PC} = \boldsymbol{0}\end{align*}すなわち、\[s\overrightarrow{CA} + t\overrightarrow{CB} = \overrightarrow{CP}\]である。
この時点では点 $P$ が $\triangle{ABC}$ に含まれているかは不明であるが、以下その点について調べよう。$\triangle{ABC}$ を下図2のように定める。
ここで、$\overrightarrow{CP}\times \overrightarrow{CA}$、$\overrightarrow{CB}\times \overrightarrow{CP}$ を計算すると\begin{align*}\overrightarrow{CP}\times \overrightarrow{CA} = (s\overrightarrow{CA} + t\overrightarrow{CB}) \times \overrightarrow{CA} = t(\overrightarrow{CB} \times \overrightarrow{CA}) \\\\\overrightarrow{CB}\times \overrightarrow{CP} = \overrightarrow{CB} \times (s\overrightarrow{CA} + t\overrightarrow{CB})= s(\overrightarrow{CB} \times \overrightarrow{CA}) \\\\\end{align*}であるが、$s, t \geq 0$ であるから、これは2つの外積 $\overrightarrow{CP}\times \overrightarrow{CA}$、$\overrightarrow{CB}\times \overrightarrow{CP}$ が $\overrightarrow{CB} \times \overrightarrow{CA}$ と同じ方向を向いていることを意味している ($\triangle{ABC}$ がXY平面上にある場合には上記の外積はいずれも z軸プラス方向)。具体的には点 $P$ が辺 $BC$ を含む直線と辺 $CA$ を含む直線に囲まれた領域の中にあるということである (図3の青い領域 ; $\triangle{ABC}$ もこの領域に含まれる)。
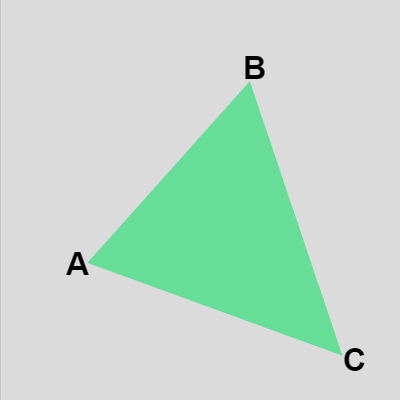
図2 $\triangle{ABC}$ 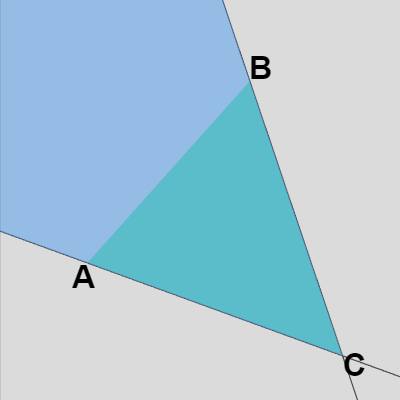
図3 青い領域 (辺 $BC$ を含む直線と辺 $CA$ を含む直線に囲まれた領域で $\triangle{ABC}$ もこの領域に含まれる)
残っている問題は点 $P$ が青い領域において、$\triangle{ABC}$ を基準として辺 $AB$ の内側にあるか外側にあるかということである。
そのために上の2つの外積を面積で表すと、\begin{align*}&|\overrightarrow{CP}\times \overrightarrow{CA}| = 2|\triangle{PCA}| = t|\overrightarrow{CB} \times \overrightarrow{CA}| = 2t|\triangle{ABC}| \\\\&|\overrightarrow{CB}\times \overrightarrow{CP}| = 2|\triangle{PBC}| = s|\overrightarrow{CB} \times \overrightarrow{CA}| = 2s|\triangle{ABC}| \end{align*}であるから、$|\triangle{PCA}| = t|\triangle{ABC}|$、$|\triangle{PBC}| = s|\triangle{ABC}|$ である。
したがって、($s+t+u = 1$ であることに注意すれば)\[|\triangle{PCA}| + |\triangle{PBC}| = (s+t)|\triangle{ABC}| \leq |\triangle{ABC}| \]であるが、これは青い領域において点 $P$ が辺 $AB$ の内側、すなわち $\triangle{ABC}$ に含まれることを意味する ($P$ が辺 $AB$ の外側にある場合には $\triangle{PCA}$ と $\triangle{PBC}$ の面積の和は明らかに $\triangle{ABC}$ の面積よりも大くなる)。
もちろんこの場合には $\triangle{PAB}$ も $\triangle{ABC}$ の内側にあるから、$\triangle{PAB}$ の面積は\begin{align*}|\triangle{PAB}| &= |\triangle{ABC}| - (|\triangle{PCA}| + |\triangle{PBC}|) \\\\&= |\triangle{ABC}| - (s+t)|\triangle{ABC}| = u|\triangle{ABC}|\end{align*}であることがわかる。
以上より (1) が成り立つとき点 $P$ は $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]である。 (証明終)
上の命題は4点がXY平面上にあることが前提であったが、実際には3次元空間内の任意の平面に拡張することができる。つまり4点 $A$、$B$、$C$、$P$ が3次元空間内の同一平面上にあるならば上記の命題を拡張した次の命題が成り立つ。
(この証明は上記証明の前半部分について補足するだけでよい。なぜなら後半は3次元空間の任意の平面の場合でも上記と同じ内容になるためである)
(上記証明の補足) 4点 $A'$、$B'$、$C'$、$P'$ を3次元空間内の同一平面上の点とし、$P'$ が $\triangle{A'B'C'}$ に含まれ、さらに\[ |\triangle{P'B'C'}| : |\triangle{P'C'A'}| : |\triangle{P'A'B'}| = s : t : u \]であるとする (ここでも簡単のため $s$、$t$、$u$ をその3つの三角形の面積とする)。
$A'$、$B'$、$C'$、$P'$ が置かれている平面をXY平面に重ねる変換を、この4つの点に実行したときの変換後の位置を $A$、$B$、$C$、$P$ で表す。この変換の逆変換を表す行列を $M$ とすれば、$A' = MA$、$B' = MB$、$C' = MC$、$P' = MP$ である (このとき明らかに $M$ は回転行列と平行移動行列の積として表される。したがって行列式は $1$ ($det M = 1$) である)。
$\overrightarrow{PA} = P - A = \boldsymbol{a}$、$\overrightarrow{P'A'} = P' - A' = \boldsymbol{a}'$ とすれば $\boldsymbol{a}' = M\boldsymbol{a}$ である。同様に $\overrightarrow{PB} = \boldsymbol{b}$、$\overrightarrow{PC} = \boldsymbol{c}$、$\overrightarrow{P'B'} = \boldsymbol{b}'$、$\overrightarrow{P'C'} = \boldsymbol{c}'$ とすれば $\boldsymbol{b}' = M\boldsymbol{b}$、$\boldsymbol{c}' = M\boldsymbol{c}$ である。また、z軸プラス方向を表す単位ベクトルを $\boldsymbol{z}$ で表し、$\boldsymbol{z}' = M\boldsymbol{z}$ とする。
(注意 : $M$ は回転と平行移動のみによって構成されるので、$\triangle{A'B'C'}$ における $P'$ の相対的な位置と $\triangle{ABC}$ における $P$ の相対的な位置は同じである。言い換えれば $P'$ が $\triangle{A'B'C'}$ に含まれていれば $P$ も $\triangle{ABC}$ に含まれており、$\triangle{P'B'C'}$、$\triangle{P'C'A'}$、$\triangle{P'A'B'}$ の面積が $s$、$t$、$u$ であれば、$\triangle{PBC}$、$\triangle{PCA}$、$\triangle{PAB}$ の面積も $s$、$t$、$u$ である)
$A$、$B$、$C$、$P$ はXY平面上の点であるから最初の命題によって (1) が成り立つ。
また $A$、$B$、$C$、$P$ はXY平面上において図1に示される関係にあるので $\overrightarrow{PC}\times \overrightarrow{PB}$、$\overrightarrow{PA}\times \overrightarrow{PC}$、$\overrightarrow{PB}\times \overrightarrow{PA}$ の方向を表す単位ベクトルはいずれも $\boldsymbol{z}$ であることに注意すれば、$2s = |\overrightarrow{PC}\times \overrightarrow{PB}|$ は $\boldsymbol{z}\cdot (\boldsymbol{c}\times \boldsymbol{b}) = det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})$ と表される ($\boldsymbol{i}$、$\boldsymbol{j}$、$\boldsymbol{k}$ を1列目、2列目、3列目に持つ $3\times 3$ 行列を $(\boldsymbol{i},\ \boldsymbol{j},\ \boldsymbol{k})$ の形で表す)。同様に $2t = |\overrightarrow{PA}\times \overrightarrow{PC}|$、$2u = |\overrightarrow{PB}\times \overrightarrow{PA}|$ はそれぞれ $det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})$、$det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})$ である。
この表し方によって (1) は以下のように書き換えられる。
\[\frac{1}{2}\left\{ det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})\boldsymbol{a} + det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})\boldsymbol{b} + det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})\boldsymbol{c} \right\} = \boldsymbol{0} \]ここで調べたいのは3次元空間内の同一平面上にある4点 $A'$、$B'$、$C'$、$P'$ に関して、以下の式が成り立つかどうかである ($s, t, u \geq 0$ であることはすでにわかっている)。
\[s\overrightarrow{P'A'} + t\overrightarrow{P'B'} + u\overrightarrow{P'C'} = \boldsymbol{0} \tag{1a} \]すぐ上で述べたことを用いればこの式は次のように書き換えられる。
この書き換えた式を使って (1a) が成り立つことを示そう。
なお、この重心座標に関する命題は別の形で書き換えられるが、最後にその点について述べておこう。
本節では重心座標 $(s,\ t,\ u)$ に関して $s+t+u = 1$ を前提としていたが、式 (1) にあらためてこの制限を明記したものを式 (2) とする。すなわち
式 (2) が成り立つとき、$t, u \geq 0$、$t+u \leq 1$ は明らかである。さらに (2) を\[s(A - P) + t(B - P) + u(C - P) = \boldsymbol{0} \]の形で表せば、
先程の命題を (3) を用いて表すと次のように言い換えられる (これは高校数学ではベクトルの終点の存在範囲と呼ばれる)。
この式の右辺の分母を払って $(s + t + u)P = sA + tB + uC$ とし、左辺を右辺に移すと、\[s(A - P) + t(B - P) + u(C - P) = \boldsymbol{0}\]すなわち、\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \tag{$B_2$} \]の形になるが、この式は単に最初の式を書き換えただけであり、やはり $(s,\ t,\ u)$ が $P$ の重心座標であることを表す式である。
定義からわかるように重心座標は一意的には決まらない。例えば3つの数 $d$、$e$、$f$ の比が $s:t:u$ であるならば $(d, e, f)$ も $(2d,\ 2e,\ 2f)$ も $P$ の重心座標である。ただし本節では簡単のため $(s, t, u)$ が重心座標であるとき各成分を'正規化'された値、具体的には $\underline{s + t + u = 1}$ であるとする。
$\triangle{ABC}$ に関して点 $P$ を重心座標で表す場合、$P$ が $\triangle{ABC}$ の内側であっても外側であっても重心座標は定義されるが、本節においては点 $P$ が $\triangle{ABC}$ に含まれる場合(内部あるいは周上にある場合)のみを対象とする。後に示すが、この場合には $P$ の重心座標の各成分はいずれも $0$ 以上の値であり($s, t, u \geq 0$)、$\triangle{ABC}$ の面積を $s+t+u$ と同じく $1$ とすれば重心座標 $(s, t, u)$ は $\triangle{PBC}$、$\triangle{PCA}$、$\triangle{PAB}$ の面積に等しくなるのである。

点 $P$ が冒頭の式 $(B_1)$ あるいは $(B_2)$ の形で表されるとき、$(s,\ t,\ u)$ を「$\triangle{ABC}$ に関する点 $P$ の重心座標」と呼ぶことにすれば、$(s,\ t,\ u)$ が $\triangle{ABC}$ に関する点 $P$ の重心座標であり、さらに $s, t, u \geq 0$ であることは次の式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]として表すことができる。
先程「$(s,\ t,\ u)$ が重心座標ならば $s+t+u = 1$ とする」と定めたが、(1) が成り立つとき $(s,\ t,\ u)$ は重心座標であるから、(1) が成り立つならば $\underline{s+t+u = 1}$ であることには注意しよう。
(重心座標は必ずしも三角形のみに定義されるものではなく、より一般の形で定義される。また本節では重心座標の各成分が $0$ 以上になる場合しか扱わないが、一般の状況においては重心座標の各成分はプラスにもマイナスにもなり得る。なお解説中の三角形についてはその各頂点が時計周り(clockwise-order)であることが前提である)
まず三角形の重心座標に関する基本的な命題を証明する。
4点 $A$、$B$、$C$、$P$ をXY平面上の点とする。
点 $P$ が $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]であるためには、以下の関係式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]が成り立つことが必要十分である。
点 $P$ が $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]であるためには、以下の関係式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]が成り立つことが必要十分である。
(証明) まず点 $P$ が $\triangle{ABC}$ に含まれ、3つの三角形の面積比が $|\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u$ であるとすれば、$0$ でない適当な実数 $k$ によってその3つの三角形の面積を $ks$、$kt$、$ku$ と置くことができる。$s$、$t$、$u$ はこの時点ではプラスかマイナスかはわかっていないが、面積比が $s:t:u$ であることからいずれも符号は同じであることに注意しよう ($s, t, u \geq 0$ あるいは $s, t, u < 0$)。
上図1から $2ks = |\overrightarrow{PC}\times \overrightarrow{PB}|$、$2kt = |\overrightarrow{PA}\times \overrightarrow{PC}|$、$2ku = |\overrightarrow{PB}\times \overrightarrow{PA}|$ である (XY平面上に置かれているから、この3つの外積はいずれも z軸プラス方向を向く)。
ここで $\overrightarrow{PA} = (a_x,\ a_y)$、$\overrightarrow{PB} = (b_x,\ b_y)$、$\overrightarrow{PC} = (c_x,\ c_y)$ と置き、以下の式を計算すると
\begin{align*}&2ks\overrightarrow{PA} + 2kt\overrightarrow{PB} + 2ku\overrightarrow{PC} \,= \,2k(s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC}) \\\\=\ &|\overrightarrow{PC}\times \overrightarrow{PB}|\,\overrightarrow{PA} + |\overrightarrow{PA}\times \overrightarrow{PC}|\,\overrightarrow{PB} + |\overrightarrow{PB}\times \overrightarrow{PA}|\,\overrightarrow{PC} \\\\=\ &(c_xb_y - c_yb_x)(a_x,\ a_y) + (a_xc_y - a_yc_x)(b_x,\ b_y) + (b_xa_y - b_ya_x)(c_x,\ c_y) \\\\=\ &(a_xb_yc_x - a_xb_xc_y,\ a_yb_yc_x - a_yb_xc_y) + (a_xb_xc_y - a_yb_xc_x,\ a_xb_yc_y - a_yb_yc_x) + (a_yb_xc_x - a_xb_yc_x,\ a_yb_xc_y - a_xb_yc_y) \\\\=\ &(0,\ 0) = \boldsymbol{0}\end{align*}
であるから、$s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0}$、すなわち冒頭の $(B_2)$ が成り立つ。$(B_2)$ が成り立つならば $s$、$t$、$u$ は重心座標であり、したがって上の取り決めにより $s+t+u = 1$ である。$s$、$t$、$u$ はいずれもプラスであるか、マイナスであるかのどちらかであったが、$s+t+u=1$ によりいずれもプラスであることがわかる。以上から (1) が成り立つことが示された。
逆に (1) が成り立つとする。
$\overrightarrow{PA} = \overrightarrow{PC} + \overrightarrow{CA}$、$\overrightarrow{PB} = \overrightarrow{PC} + \overrightarrow{CB}$ であるから (1) より、\begin{align*}&s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} \\\\=\ &s(\overrightarrow{PC} + \overrightarrow{CA}) + t(\overrightarrow{PC} + \overrightarrow{CB}) + u\overrightarrow{PC} \\\\=\ &s\overrightarrow{CA} + t\overrightarrow{CB} + (s+t+u)\overrightarrow{PC} \\\\=\ &s\overrightarrow{CA} + t\overrightarrow{CB} + \overrightarrow{PC} = \boldsymbol{0}\end{align*}すなわち、\[s\overrightarrow{CA} + t\overrightarrow{CB} = \overrightarrow{CP}\]である。
この時点では点 $P$ が $\triangle{ABC}$ に含まれているかは不明であるが、以下その点について調べよう。$\triangle{ABC}$ を下図2のように定める。
ここで、$\overrightarrow{CP}\times \overrightarrow{CA}$、$\overrightarrow{CB}\times \overrightarrow{CP}$ を計算すると\begin{align*}\overrightarrow{CP}\times \overrightarrow{CA} = (s\overrightarrow{CA} + t\overrightarrow{CB}) \times \overrightarrow{CA} = t(\overrightarrow{CB} \times \overrightarrow{CA}) \\\\\overrightarrow{CB}\times \overrightarrow{CP} = \overrightarrow{CB} \times (s\overrightarrow{CA} + t\overrightarrow{CB})= s(\overrightarrow{CB} \times \overrightarrow{CA}) \\\\\end{align*}であるが、$s, t \geq 0$ であるから、これは2つの外積 $\overrightarrow{CP}\times \overrightarrow{CA}$、$\overrightarrow{CB}\times \overrightarrow{CP}$ が $\overrightarrow{CB} \times \overrightarrow{CA}$ と同じ方向を向いていることを意味している ($\triangle{ABC}$ がXY平面上にある場合には上記の外積はいずれも z軸プラス方向)。具体的には点 $P$ が辺 $BC$ を含む直線と辺 $CA$ を含む直線に囲まれた領域の中にあるということである (図3の青い領域 ; $\triangle{ABC}$ もこの領域に含まれる)。


残っている問題は点 $P$ が青い領域において、$\triangle{ABC}$ を基準として辺 $AB$ の内側にあるか外側にあるかということである。
そのために上の2つの外積を面積で表すと、\begin{align*}&|\overrightarrow{CP}\times \overrightarrow{CA}| = 2|\triangle{PCA}| = t|\overrightarrow{CB} \times \overrightarrow{CA}| = 2t|\triangle{ABC}| \\\\&|\overrightarrow{CB}\times \overrightarrow{CP}| = 2|\triangle{PBC}| = s|\overrightarrow{CB} \times \overrightarrow{CA}| = 2s|\triangle{ABC}| \end{align*}であるから、$|\triangle{PCA}| = t|\triangle{ABC}|$、$|\triangle{PBC}| = s|\triangle{ABC}|$ である。
したがって、($s+t+u = 1$ であることに注意すれば)\[|\triangle{PCA}| + |\triangle{PBC}| = (s+t)|\triangle{ABC}| \leq |\triangle{ABC}| \]であるが、これは青い領域において点 $P$ が辺 $AB$ の内側、すなわち $\triangle{ABC}$ に含まれることを意味する ($P$ が辺 $AB$ の外側にある場合には $\triangle{PCA}$ と $\triangle{PBC}$ の面積の和は明らかに $\triangle{ABC}$ の面積よりも大くなる)。
もちろんこの場合には $\triangle{PAB}$ も $\triangle{ABC}$ の内側にあるから、$\triangle{PAB}$ の面積は\begin{align*}|\triangle{PAB}| &= |\triangle{ABC}| - (|\triangle{PCA}| + |\triangle{PBC}|) \\\\&= |\triangle{ABC}| - (s+t)|\triangle{ABC}| = u|\triangle{ABC}|\end{align*}であることがわかる。
以上より (1) が成り立つとき点 $P$ は $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]である。 (証明終)
上の命題は4点がXY平面上にあることが前提であったが、実際には3次元空間内の任意の平面に拡張することができる。つまり4点 $A$、$B$、$C$、$P$ が3次元空間内の同一平面上にあるならば上記の命題を拡張した次の命題が成り立つ。
4点 $A$、$B$、$C$、$P$ を3次元空間内の同一平面上の点とする。
点 $P$ が $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]であるためには、以下の関係式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]が成り立つことが必要十分である。
点 $P$ が $\triangle{ABC}$ に含まれ、さらに\[ |\triangle{PBC}| : |\triangle{PCA}| : |\triangle{PAB}| = s : t : u \]であるためには、以下の関係式\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0) \tag{1}\]が成り立つことが必要十分である。
(この証明は上記証明の前半部分について補足するだけでよい。なぜなら後半は3次元空間の任意の平面の場合でも上記と同じ内容になるためである)
(上記証明の補足) 4点 $A'$、$B'$、$C'$、$P'$ を3次元空間内の同一平面上の点とし、$P'$ が $\triangle{A'B'C'}$ に含まれ、さらに\[ |\triangle{P'B'C'}| : |\triangle{P'C'A'}| : |\triangle{P'A'B'}| = s : t : u \]であるとする (ここでも簡単のため $s$、$t$、$u$ をその3つの三角形の面積とする)。
$A'$、$B'$、$C'$、$P'$ が置かれている平面をXY平面に重ねる変換を、この4つの点に実行したときの変換後の位置を $A$、$B$、$C$、$P$ で表す。この変換の逆変換を表す行列を $M$ とすれば、$A' = MA$、$B' = MB$、$C' = MC$、$P' = MP$ である (このとき明らかに $M$ は回転行列と平行移動行列の積として表される。したがって行列式は $1$ ($det M = 1$) である)。
$\overrightarrow{PA} = P - A = \boldsymbol{a}$、$\overrightarrow{P'A'} = P' - A' = \boldsymbol{a}'$ とすれば $\boldsymbol{a}' = M\boldsymbol{a}$ である。同様に $\overrightarrow{PB} = \boldsymbol{b}$、$\overrightarrow{PC} = \boldsymbol{c}$、$\overrightarrow{P'B'} = \boldsymbol{b}'$、$\overrightarrow{P'C'} = \boldsymbol{c}'$ とすれば $\boldsymbol{b}' = M\boldsymbol{b}$、$\boldsymbol{c}' = M\boldsymbol{c}$ である。また、z軸プラス方向を表す単位ベクトルを $\boldsymbol{z}$ で表し、$\boldsymbol{z}' = M\boldsymbol{z}$ とする。
(注意 : $M$ は回転と平行移動のみによって構成されるので、$\triangle{A'B'C'}$ における $P'$ の相対的な位置と $\triangle{ABC}$ における $P$ の相対的な位置は同じである。言い換えれば $P'$ が $\triangle{A'B'C'}$ に含まれていれば $P$ も $\triangle{ABC}$ に含まれており、$\triangle{P'B'C'}$、$\triangle{P'C'A'}$、$\triangle{P'A'B'}$ の面積が $s$、$t$、$u$ であれば、$\triangle{PBC}$、$\triangle{PCA}$、$\triangle{PAB}$ の面積も $s$、$t$、$u$ である)
$A$、$B$、$C$、$P$ はXY平面上の点であるから最初の命題によって (1) が成り立つ。
また $A$、$B$、$C$、$P$ はXY平面上において図1に示される関係にあるので $\overrightarrow{PC}\times \overrightarrow{PB}$、$\overrightarrow{PA}\times \overrightarrow{PC}$、$\overrightarrow{PB}\times \overrightarrow{PA}$ の方向を表す単位ベクトルはいずれも $\boldsymbol{z}$ であることに注意すれば、$2s = |\overrightarrow{PC}\times \overrightarrow{PB}|$ は $\boldsymbol{z}\cdot (\boldsymbol{c}\times \boldsymbol{b}) = det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})$ と表される ($\boldsymbol{i}$、$\boldsymbol{j}$、$\boldsymbol{k}$ を1列目、2列目、3列目に持つ $3\times 3$ 行列を $(\boldsymbol{i},\ \boldsymbol{j},\ \boldsymbol{k})$ の形で表す)。同様に $2t = |\overrightarrow{PA}\times \overrightarrow{PC}|$、$2u = |\overrightarrow{PB}\times \overrightarrow{PA}|$ はそれぞれ $det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})$、$det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})$ である。
この表し方によって (1) は以下のように書き換えられる。
\[\frac{1}{2}\left\{ det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})\boldsymbol{a} + det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})\boldsymbol{b} + det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})\boldsymbol{c} \right\} = \boldsymbol{0} \]ここで調べたいのは3次元空間内の同一平面上にある4点 $A'$、$B'$、$C'$、$P'$ に関して、以下の式が成り立つかどうかである ($s, t, u \geq 0$ であることはすでにわかっている)。
\[s\overrightarrow{P'A'} + t\overrightarrow{P'B'} + u\overrightarrow{P'C'} = \boldsymbol{0} \tag{1a} \]すぐ上で述べたことを用いればこの式は次のように書き換えられる。
\begin{align*}&|\triangle{P'B'C'}|\,\overrightarrow{P'A'} + |\triangle{P'C'A'}|\,\overrightarrow{P'B'} + |\triangle{P'A'B'}|\,\overrightarrow{P'C'} \\\\=\ &\frac{1}{2}\left( |\overrightarrow{P'C'}\times \overrightarrow{P'B'}|\,\overrightarrow{P'A'} + |\overrightarrow{P'A'}\times \overrightarrow{P'C'}|\,\overrightarrow{P'B'} + |\overrightarrow{P'B'}\times \overrightarrow{P'A'}|\,\overrightarrow{P'C'} \right) \\\\=\ &\frac{1}{2}\left\{ det(\boldsymbol{c}',\ \boldsymbol{b}',\ \boldsymbol{z}')\boldsymbol{a}' + det(\boldsymbol{a}',\ \boldsymbol{c}',\ \boldsymbol{z}')\boldsymbol{b}' + det(\boldsymbol{b}',\ \boldsymbol{a}',\ \boldsymbol{z}')\boldsymbol{c}' \right\} \\\\=\ &\boldsymbol{0} \end{align*}
この書き換えた式を使って (1a) が成り立つことを示そう。
\begin{align*}&det(\boldsymbol{c}',\ \boldsymbol{b}',\ \boldsymbol{z}')\boldsymbol{a}' + det(\boldsymbol{a}',\ \boldsymbol{c}',\ \boldsymbol{z}')\boldsymbol{b}' + det(\boldsymbol{b}',\ \boldsymbol{a}',\ \boldsymbol{z}')\boldsymbol{c}' \\\\=\ &det\{M(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})\}M\boldsymbol{a} + det\{M(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})\}M\boldsymbol{b} + det\{M(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})\}M\boldsymbol{c} \\\\=\ &detM\,det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})M\boldsymbol{a} + detM\,det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})M\boldsymbol{b} + detM\,det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})M\boldsymbol{c} \\\\=\ &M\{det(\boldsymbol{c},\ \boldsymbol{b},\ \boldsymbol{z})\boldsymbol{a} + det(\boldsymbol{a},\ \boldsymbol{c},\ \boldsymbol{z})\boldsymbol{b} + det(\boldsymbol{b},\ \boldsymbol{a},\ \boldsymbol{z})\boldsymbol{c}\} \\\\=\ &M\boldsymbol{0}\ =\ \boldsymbol{0}\end{align*}
以上から3次元空間の任意の平面に拡張できることがわかる。なお、この重心座標に関する命題は別の形で書き換えられるが、最後にその点について述べておこう。
本節では重心座標 $(s,\ t,\ u)$ に関して $s+t+u = 1$ を前提としていたが、式 (1) にあらためてこの制限を明記したものを式 (2) とする。すなわち
\[s\overrightarrow{PA} + t\overrightarrow{PB} + u\overrightarrow{PC} = \boldsymbol{0} \qquad (s, t, u \geq 0\ \ ,\ \ s+t+u=1) \tag{2}\]
である。式 (2) が成り立つとき、$t, u \geq 0$、$t+u \leq 1$ は明らかである。さらに (2) を\[s(A - P) + t(B - P) + u(C - P) = \boldsymbol{0} \]の形で表せば、
\[s(P - A) = \{1 - (t + u)\}(P - A) = t(B - P) + u(C - P)\]
であるから、これを次のように変形する。\begin{align*}P - A &= (t + u)(P - A) + t(B - P) + u(C - P) \\\\&= t(B - P + P - A) + u(C - P + P - A) \\\\&= t(B - A) + u(C - A)\end{align*}すなわち、(2) が成り立つならば\[\overrightarrow{AP} = t\overrightarrow{AB} + u\overrightarrow{AC} \qquad (\,t, u \geq 0\ \ ,\ \ t+u \leq 1) \qquad \tag{3} \]
が成り立つ。逆に (3) が成り立つならば、$s = 1 - (t+u)$ と置いて、今述べたことを逆にたどっていけば (2) が成り立つことが示されるから結局、(2) と (3) は同値な表現であることがわかる。先程の命題を (3) を用いて表すと次のように言い換えられる (これは高校数学ではベクトルの終点の存在範囲と呼ばれる)。
3次元空間内の同一平面上にある4点 $A$、$B$、$C$、$P$ に関して、点 $P$ が $\triangle{ABC}$ に含まれるためには\[\overrightarrow{AP} = t\overrightarrow{AB} + u\overrightarrow{AC} \qquad (\,t, u \geq 0\ \ ,\ \ t+u \leq 1)\]であることが必要十分である。
14-4 >>
Möller-Trumbore algorithm (レイ vs 三角形)
Möller-Trumbore algorithm (レイ vs 三角形)
© 2020-2025 Redpoll's 60 (All rights reserved)