Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-9
第4章 3D空間におけるオブジェクトの運動
$§$4-9 ローカル座標系とワールド座標系 2
前節の続きである。
本節においても、以下の2つのオブジェクトを使用して階層構造と各階層における座標系について見ていく。
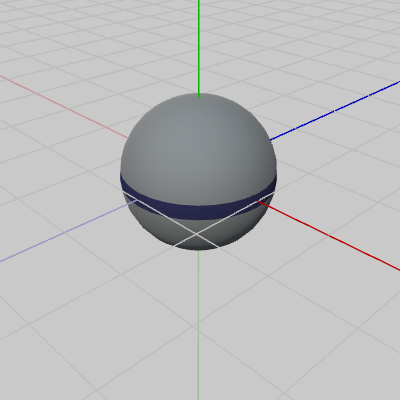
図1 Sphere 初期状態 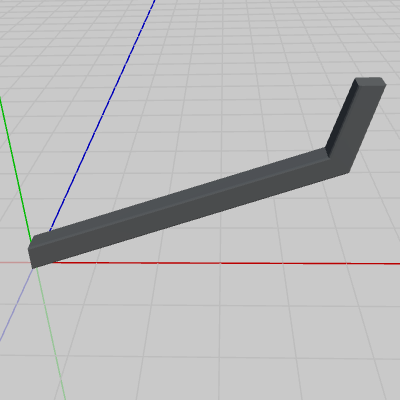
図2 Arm 初期状態
[Code1] (実行結果 図1、図2、図3)
図3は、プログラムの実行結果をワールド座標系から見たときの様子である。図3における数値はすべてワールド座標系での値であり、W(##, ##, ##) はワールド座標系の座標値を表している。Armは、$(3, 0, -3)$だけ平行移動したため、原点にあったArmの支点は、ワールド座標系において $(3, 0, -3)$ に移動しており、Armにアタッチされている Sphereの中心は $(8, 4, -3)$ に移動している。Arm座標系も同じだけの平行移動を行っているが、平行移動をしただけなのでA-x軸、A-z軸はワールド座標系のx軸、z軸と平行である。
図4は、プログラムの実行結果を Arm座標系から見たときの様子である。図4における数値はすべてArm座標系での値であり、A(##, ##, ##) は Arm座標系の座標値を表している。Arm座標系では、Armの支点は原点にあり、Armは初期状態と同じ状態である。前節でも述べたが、オブジェクトに変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトの状態(位置、向き、大きさ)は変化しないのである。
Sphereの中心は Arm座標系では $(5, 4, 0)$ にある。つまり、Armを動かした場合でも、Armにアタッチされている Sphereは Arm座標系においては、アタッチされた場所から動いていないことがわかる。
前節でも述べたように、オブジェクトが運動する際は、そのオブジェクトのローカル座標系も一体となって運動する。ここでは、Armを平行移動させているが、Arm座標系も それと同じだけの移動をするので、Arm座標系内の2つのオブジェクトは、Arm座標系の中では何も変化がないのである。
図5は、プログラムの実行結果を Sphere座標系から見たときの様子である。やはり、Sphereも自身のローカル座標系の中では初期状態から変化がない。今回の Armの移動では、子オブジェクトである Sphereも Armと一体化して移動するが、その際に、Sphereのローカル座標系もまた、Sphereと一体となって移動するためである。
どのようなときでもオブジェクトのローカル座標系は、オブジェクトと一体となって運動するのである。
ワールド座標系内の軸mの周りに Armを回転させることは、手順的には図7に示されるように Armをワールド座標系のy軸周りに回転させてから、$(3, 0, -3)$ だけ平行移動させるという順序になるが、その一連の運動の過程においても、ローカル座標系はオブジェクトと一体となって運動する (図7においても Arm座標系は Armと一体となって運動している)。

図6 軸m ( (3, 0, -3)を通り、y軸に平行 ; Armは(3, 0, -3)移動しただけで、軸m周りの回転を行っていない状態) 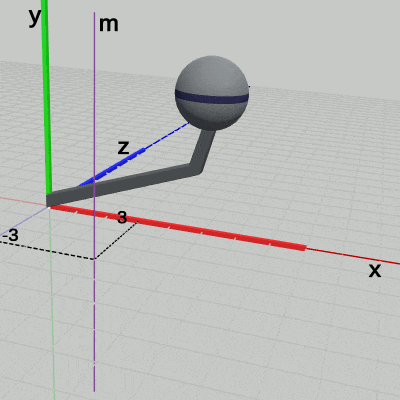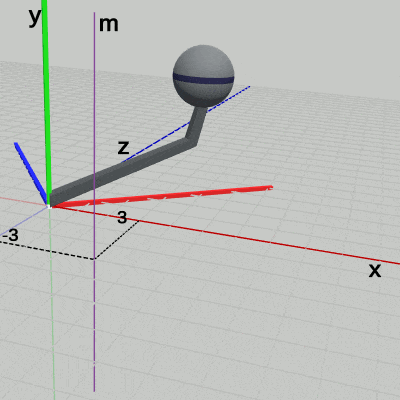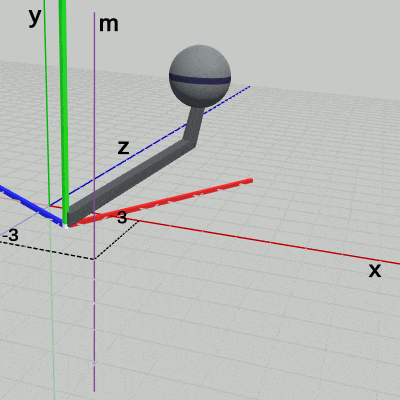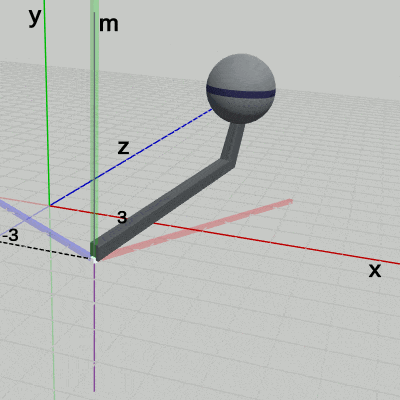
図7 Armをy軸周りに-60°回転させ、(3, 0, -3)だけ平行移動させる (結果的には軸mの周りに-60°回転した状態になる)
[Code2] (実行結果 図8、図9、図10)
(以下の実行結果では、軸mが Arm座標系の y軸と重なっていることに注意)
図8は、プログラムの実行結果をワールド座標系から見たときの様子である (図8における数値は、すべてワールド座標系での値である)。Armの支点が $(3, 0, -3)$ にあるのは前回のプログラムと同じであるが、今回は その支点の周りに Armを $-60$°回転させているため Arm座標系のA-x軸、A-z軸がワールド座標系のx軸、z軸と平行ではない、また、Armの先端にある Sphereの(中心の)座標も変化している。今回の変換による、Sphereの中心の座標は次のように求められる。
この変換は まずワールド座標系のy軸周りに Armを回転させてから、$(3, 0, -3)$ だけ平行移動するという手順である(図7参照)。Armが原点に置かれているときの、Sphereの中心の座標は $(5, 4, 0)$ であるから、その座標を $-60$°回転させて $(3, 0, -3)$ だけ平行移動させると (以下の式中の一番左の行列が平行移動行列であり、その隣の行列が $-60$°の回転行列である)、
図9、図10は、Arm座標系、Sphere座標系からプログラムの実行結果を見たときの様子である。それぞれの座標系における、オブジェクトの位置は今までのものと変わりはない。
[Code3] (実行結果 図11、図12、図13)
図11、図12、図13は、プログラムの実行結果をそれぞれ、ワールド座標系、Arm座標系、Sphere座標系から見たときの様子である。図11、図12と前回の実行結果である図8、図9とを見比べれば、明らかに Sphereが拡大されているのがわかるであろう。特に、Arm座標系での表示を見比べた場合、図9における Sphereの半径は $1$であるが、図12においては Sphereが $2$倍拡大されているため半径は $2$になっている。
図13の Sphere座標系から見たときの Sphereは、今までのものと特に変わりはない。オブジェクトは、自身のローカル座標系の中では位置、向き、大きさなどの状態は変化しない ということがここでも示されている。
前節でも述べたが、オブジェクトの運動は、そのオブジェクトの親座標系の中で定義することが基本である。今回のプログラムを例にとって、そのことについて説明しよう。
今回の Sphereに定義された変換は、Armの先端で$2$倍拡大するというものであった。プログラムでは Code3の1行目から3行目の部分で、実行手順は、まず原点において$2$拡大(sclSphere)、そして Armの先端(Arm座標系の $(5, 4, 0)$ )にアタッチ(traSphere)という順序である。この変換は結果的には、$(5, 4, 0)$だけ平行移動した地点において$2$倍拡大した状態になる。
そして肝心なことは、Sphereに定義された これらの変換は、Sphereの親座標系である Arm座標系の中で実行されるということである。図12に示されているように、Sphereは、Arm座標系の中で $2$倍に拡大し、Arm座標系の中で $(5, 4, 0)$に移動するのである。実際、他の座標系で見た場合、たとえば図11のワールド座標系では Sphereは$2$倍に拡大されてはいるが Sphereの(中心の)位置は $(5.5, 4.0, 1.33)$ であり、図13の Sphere座標系では Sphereの位置は原点から動いていない、さらに Sphere座標系における Sphereの半径の大きさ $1$のままである。つまり、ワールド座標系や Sphere座標系からでは Sphereに対して定義された「$(5, 4, 0)$だけ平行移動した地点において$2$倍拡大」という変換は見えないのである。
Armの場合も同様である。Armに定義された変換は、$(3, 0, -3)$ だけ移動し、その場所において Armの支点を通る軸mの周りに $-60$°回転するというものであった。プログラムでは Code3の5行目から7行目の部分で、実行手順は、まず原点においてy軸周りに $-60$°の回転(rotArm)、そして $(3, 0, -3)$ の平行移動(traArm)という順序である。Armは親オブジェクトを持たないので、前節で述べたように親座標系はワールド座標系になる。したがって、この2つの変換はワールド座標系の中で実行されることになる。
実際、図11では Armの支点が $(3, 0, -3)$ に移動しており、さらにその支点の周りに Armは $-60$°回転している(図を見ただけでは回転角度までは分からないが)。これらの変換は、Armの親座標系であるワールド座標系の中で起こっていることなのである。
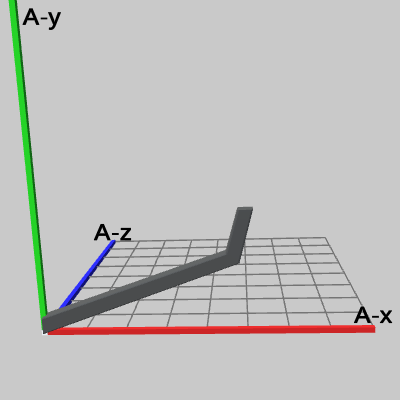
図14 例えば、図12は同じプログラムの実行結果を Arm座標系から見たときのものだが、この図から Armと Arm座標系以外を取り除いて表示したものが図14である。この図からわかるように、Arm座標系の中での Armは、平行移動も回転も行われていない初期状態のままである。本節冒頭の図2は、Armの初期状態を表示したものであるが、図14では同じものをやや離れた位置から見ているに過ぎない。
何度か述べているように、オブジェクトにどのような変換を実行しても、オブジェクトは、自身のローカル座標系の中では位置、向き、大きさなどの状態は変化しない、言い換えれば、自身のローカル座標系の中では初期状態から変わらないのである。
ここで1つ問題。
Sphereが $2$倍に拡大したので、それに伴って Sphere座標系も $2$倍に拡大した。これを明らかにしたものが、以下の図である。
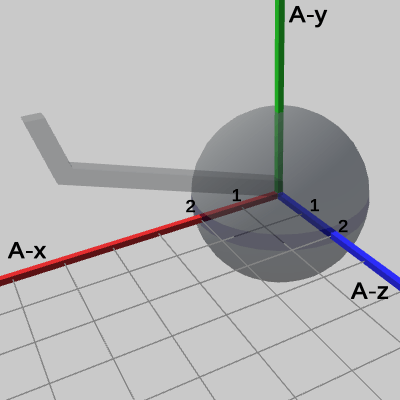
図15 2倍に拡大されたSphereを Arm座標系から見たときの様子 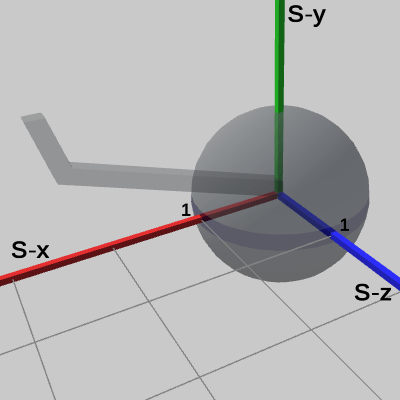
図16 2倍に拡大されたSphereを Sphere座標系から見たときの様子
この図は前節でも使用したものだが、図15は、$2$倍拡大されたSphereを Armの先端から Armの支点に移動させて、Arm座標系のみを表示したときの様子で、図16は、図15の状態から Arm座標系を非表示にし、Sphere座標系のみを表示したときの様子である。図からわかるように、Sphere座標系が $2$倍拡大したことにより、グリッドの1マス1マスの大きさが、Arm座標系のものよりも $2$倍拡大されている。
一方、Armに対しては スケールを実行していないので Armは拡大も、縮小もしていない。したがって、Arm座標系も同様に拡大、縮小は行われていない。それは、Arm座標系と その親座標系であるワールド座標系のサイズが同じであることを意味する。「サイズが同じ」とは、ここでは座標系のグリッドの1マス1マスの大きさが同じであるという意味である。実際、本節の図4を見れば、Arm座標系のグリッドが、ワールド座標系のグリッドの一部とぴたりと重なっていることがわかるであろう。
Arm座標系とワールド座標系のサイズが同じであるため、Code3実行後では、ワールド座標系においても Sphereの半径は $2$である。
ここで、Armに対して Sphereと同じように $2$倍の拡大を実行したとしよう。具体的には、Code3では7行目が以下のように記述されているが、
それを、次のように変更するのである。
上のコードに追加されている sclArm とは、2倍に拡大するスケール行列を表している。
では、もしCode3を このように変更したとき、Arm座標系における Sphereの半径、ワールド座標系における Sphereの半径は、それぞれいくつになるであろうか。
(次の事柄を考えれば、容易に答えは出る。Armを $2$倍に拡大すると、Arm座標系も $2$倍に拡大する。さらに、Armにアタッチされている Sphereも $2$倍に拡大する。)
すなわち、Armを $(3,0,−3)$だけ移動させた状態で、Armの支点を通り、ワールド座標系のy軸に平行な軸(図6の軸m)の周りに Armを回転させる。そのとき、回転する Armの先端では、Sphereが拡大縮小をしている(倍率は $1$倍から $2$倍)。
[Code4] (実行結果 図17、図18、図19)
前節のCode3と同様に、1行目の i_shmSphereは 2行目の単振動の計算で用いられる角度で、このプログラムでは毎フレーム $1$°ずつ増加する。また、この計算によって scaleは $1$から $2$の間を往復する。7行目の i_degArmは、Armの回転角度で、毎フレーム $1$°ずつ減少する。したがって、Armはワールド座標系において毎フレーム、反時計回りに $1$°ずつ回転する (これは 図17のように、Armを見下ろす位置で見た場合である。もし Armを見上げる位置で、つまり Armの下側から見た場合は Armの回転は時計回りである)。
図17は、プログラムの実行結果をワールド座標系から見たときの様子である。Armは、$(3, 0, -3)$だけ平行移動し、その場所において、Armの支点周りに回転をしている。この $(3, 0, -3)$の平行移動と、支点周りの回転は、プログラムにおける7行目から10行目に記述されており、この2つの変換が Armに対して定義されている変換である。そして、これらの定義された変換は、Armの親座標系であるワールド座標系の中で実行されるのである。$(3, 0, -3)$だけ移動するのも、移動した場所において、支点周りに回転するのもワールド座標系の中で起こっていることである。言い換えれば、Armに対して定義されたこれらの変換の内容は、ワールド座標系の中で見えるのである。たとえば、図18の Arm座標系の中での Armは平行移動も回転もしていない。つまり、Arm座標系から見た場合は Armにどのような変換が定義されているかは見えないのである。
図18は、プログラムの実行結果を Arm座標系から見たときの様子である。周囲の風景が動いているが、Arm座標系における Armには何の変化も見られない (初期状態から変化しない ;「周囲の風景が動いている」という表現は、あまり適切ではない。実際には、図17に示されるように、Armの回転に伴って Arm座標系も回転している。その回転している Arm座標系にカメラを固定しているので、周囲の風景、つまりワールド座標系が動いているように見えるのである)。
Sphereは Arm座標系におけるアタッチポジションである $(5, 4, 0)$で、$1$倍から$2$倍の拡大縮小を繰り返している。この $(5, 4, 0)$の平行移動と、$1$倍から $2$倍の間の拡大縮小は、プログラムにおける1行目から5行目に記述されており、この2つの変換が Sphereに対して定義されている変換である。そして、これらの変換は、Sphereの親座標系である Arm座標系の中で実行されるのである。$(5, 4, 0)$だけ移動するのも、移動した場所において $1$倍から $2$倍の拡大縮小をするのも、Arm座標系の中で起こっている変換なのである。たとえば、図17に示されるように、ワールド座標系の中では、Sphereは、$(3, 4, -3)$を中心とする半径 $5$の円周上を拡大縮小しながら公転している。また、図19に示されるように、Sphere座標系の中では、Sphereは、常に中心が原点にある半径$1$の球(初期状態)のままである。つまり、ワールド座標系や Sphere座標系からでは、「$(5, 4, 0)$だけ移動して、その場所において$1$倍から $2$倍の拡大縮小をする」という変換は見えないのである。
図19は、プログラムの実行結果を Sphere座標系から見たときの様子である。Sphereは拡大縮小しているが、Sphere座標系も同じだけの拡大縮小をしているので、Sphere座標系の中では、Sphereの半径は常に $1$である。また、その位置は Sphere座標系の原点から動かない。つまり、Sphere座標系における Sphereは初期状態のままである。
本節においても、以下の2つのオブジェクトを使用して階層構造と各階層における座標系について見ていく。


# Code1
前節においては、Armは初期状態から動かさなかったが、最初のプログラムでは、Sphereを Armにアタッチした状態で、Armを $(3, 0, -3)$ だけ平行移動させる (プログラム自体は前節のCode1と一箇所を除いて同じである。前節では5行目の localArmに identity行列をセットしたが、ここでは $(3, 0, -3)$ だけ移動させる平行移動行列をセットしている)。[Code1] (実行結果 図1、図2、図3)
// c_attachPos_Sphere : (5, 4, 0) Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); Matrix4x4 localSphere = traSphere; Matrix4x4 localArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 worldSphere = localArm * localSphere; Matrix4x4 worldArm = localArm; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm);
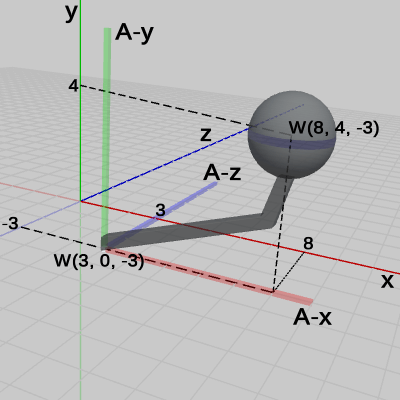 図3 Code1 実行結果 (ワールド座標系から見たときの様子)
図3 Code1 実行結果 (ワールド座標系から見たときの様子) 図4 Code1 実行結果 (Arm座標系から見たときの様子)
図4 Code1 実行結果 (Arm座標系から見たときの様子)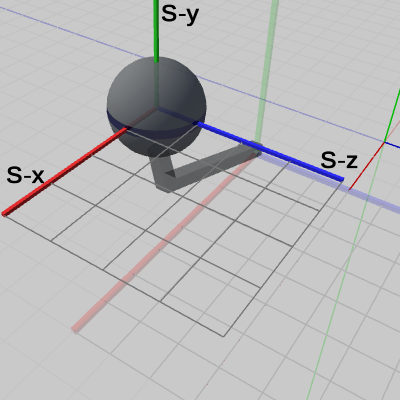 図5 Code1 実行結果 (Sphere座標系から見たときの様子)
図5 Code1 実行結果 (Sphere座標系から見たときの様子)
図3は、プログラムの実行結果をワールド座標系から見たときの様子である。図3における数値はすべてワールド座標系での値であり、W(##, ##, ##) はワールド座標系の座標値を表している。Armは、$(3, 0, -3)$だけ平行移動したため、原点にあったArmの支点は、ワールド座標系において $(3, 0, -3)$ に移動しており、Armにアタッチされている Sphereの中心は $(8, 4, -3)$ に移動している。Arm座標系も同じだけの平行移動を行っているが、平行移動をしただけなのでA-x軸、A-z軸はワールド座標系のx軸、z軸と平行である。
図4は、プログラムの実行結果を Arm座標系から見たときの様子である。図4における数値はすべてArm座標系での値であり、A(##, ##, ##) は Arm座標系の座標値を表している。Arm座標系では、Armの支点は原点にあり、Armは初期状態と同じ状態である。前節でも述べたが、オブジェクトに変換を実行しても、そのオブジェクトのローカル座標系の中では、オブジェクトの状態(位置、向き、大きさ)は変化しないのである。
Sphereの中心は Arm座標系では $(5, 4, 0)$ にある。つまり、Armを動かした場合でも、Armにアタッチされている Sphereは Arm座標系においては、アタッチされた場所から動いていないことがわかる。
前節でも述べたように、オブジェクトが運動する際は、そのオブジェクトのローカル座標系も一体となって運動する。ここでは、Armを平行移動させているが、Arm座標系も それと同じだけの移動をするので、Arm座標系内の2つのオブジェクトは、Arm座標系の中では何も変化がないのである。
図5は、プログラムの実行結果を Sphere座標系から見たときの様子である。やはり、Sphereも自身のローカル座標系の中では初期状態から変化がない。今回の Armの移動では、子オブジェクトである Sphereも Armと一体化して移動するが、その際に、Sphereのローカル座標系もまた、Sphereと一体となって移動するためである。
どのようなときでもオブジェクトのローカル座標系は、オブジェクトと一体となって運動するのである。
# Code2
次に、Armを $(3, 0, -3)$だけ移動させた位置において、図6に示される軸mの周りに Armを$-60$°回転させた状態にする (軸mは$(3, 0, -3)$を通りワールド座標系のy軸に平行な軸)。ワールド座標系内の軸mの周りに Armを回転させることは、手順的には図7に示されるように Armをワールド座標系のy軸周りに回転させてから、$(3, 0, -3)$ だけ平行移動させるという順序になるが、その一連の運動の過程においても、ローカル座標系はオブジェクトと一体となって運動する (図7においても Arm座標系は Armと一体となって運動している)。


[Code2] (実行結果 図8、図9、図10)
// c_attachPos_Sphere : (5, 4, 0) Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); Matrix4x4 localSphere = traSphere; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(-60, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 localArm = traArm * rotArm; Matrix4x4 worldSphere = localArm * localSphere; Matrix4x4 worldArm = localArm; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm);
(以下の実行結果では、軸mが Arm座標系の y軸と重なっていることに注意)
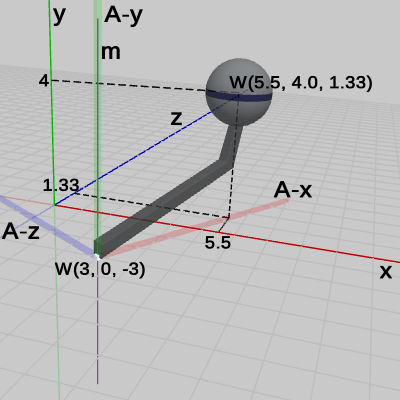 図8 Code2 実行結果 (ワールド座標系から見たときの様子)
図8 Code2 実行結果 (ワールド座標系から見たときの様子) 図9 Code2 実行結果 (Arm座標系から見たときの様子)
図9 Code2 実行結果 (Arm座標系から見たときの様子)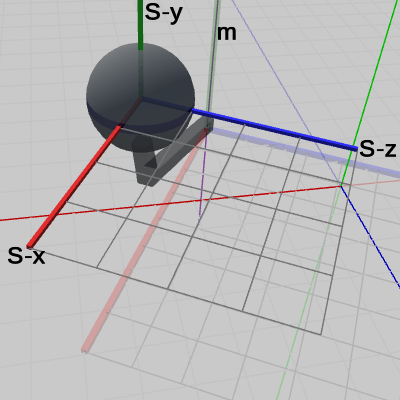 図10 Code2 実行結果 (Sphere座標系から見たときの様子)
図10 Code2 実行結果 (Sphere座標系から見たときの様子)
図8は、プログラムの実行結果をワールド座標系から見たときの様子である (図8における数値は、すべてワールド座標系での値である)。Armの支点が $(3, 0, -3)$ にあるのは前回のプログラムと同じであるが、今回は その支点の周りに Armを $-60$°回転させているため Arm座標系のA-x軸、A-z軸がワールド座標系のx軸、z軸と平行ではない、また、Armの先端にある Sphereの(中心の)座標も変化している。今回の変換による、Sphereの中心の座標は次のように求められる。
この変換は まずワールド座標系のy軸周りに Armを回転させてから、$(3, 0, -3)$ だけ平行移動するという手順である(図7参照)。Armが原点に置かれているときの、Sphereの中心の座標は $(5, 4, 0)$ であるから、その座標を $-60$°回転させて $(3, 0, -3)$ だけ平行移動させると (以下の式中の一番左の行列が平行移動行列であり、その隣の行列が $-60$°の回転行列である)、
\[\begin{pmatrix}1 &0 &0 &3 \\0 &1 &0 &0 \\ 0 &0 &1 &-3 \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}0.50 &0.00 &-0.866 &0.00 \\ 0.00 &1.00 &0.00 &0.00 \\ 0.866 &0.00 &0.50 &0.00 \\ 0.00 &0.00 &0.00 &1.00\end{pmatrix}\begin{pmatrix}5 \\4 \\0 \\1\end{pmatrix}=\begin{pmatrix}5.5 \\4.0 \\1.33 \\1\end{pmatrix}\]
となるが、この値が今回の変換後の Sphereの中心の座標である。図9、図10は、Arm座標系、Sphere座標系からプログラムの実行結果を見たときの様子である。それぞれの座標系における、オブジェクトの位置は今までのものと変わりはない。
# Code3
次に、Code2の状態から Arm先端の Sphereを2倍拡大する。[Code3] (実行結果 図11、図12、図13)
Matrix4x4 sclSphere = TH3DMath.GetScale4x4(2.0f); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); // c_attachPos_Sphere : (5, 4, 0) Matrix4x4 localSphere = traSphere * sclSphere; Matrix4x4 rotArm = TH3DMath.GetRotation4x4(-60, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 localArm = traArm * rotArm; Matrix4x4 worldSphere = localArm * localSphere; Matrix4x4 worldArm = localArm; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm);
 図11 Code3 実行結果 (ワールド座標系から見たときの様子)
図11 Code3 実行結果 (ワールド座標系から見たときの様子)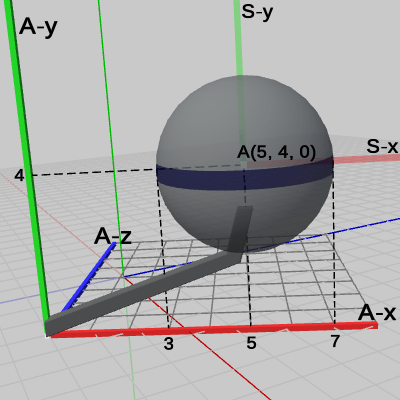 図12 Code3 実行結果 (Arm座標系から見たときの様子)
図12 Code3 実行結果 (Arm座標系から見たときの様子)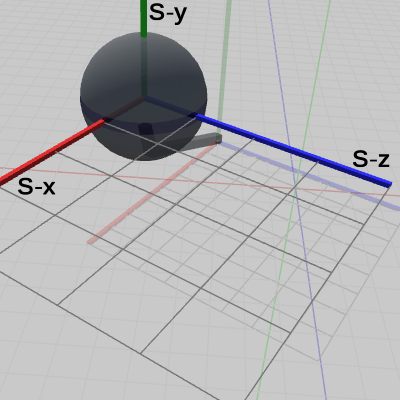 図13 Code3 実行結果 (Sphere座標系から見たときの様子)
図13 Code3 実行結果 (Sphere座標系から見たときの様子)
図11、図12、図13は、プログラムの実行結果をそれぞれ、ワールド座標系、Arm座標系、Sphere座標系から見たときの様子である。図11、図12と前回の実行結果である図8、図9とを見比べれば、明らかに Sphereが拡大されているのがわかるであろう。特に、Arm座標系での表示を見比べた場合、図9における Sphereの半径は $1$であるが、図12においては Sphereが $2$倍拡大されているため半径は $2$になっている。
図13の Sphere座標系から見たときの Sphereは、今までのものと特に変わりはない。オブジェクトは、自身のローカル座標系の中では位置、向き、大きさなどの状態は変化しない ということがここでも示されている。
前節でも述べたが、オブジェクトの運動は、そのオブジェクトの親座標系の中で定義することが基本である。今回のプログラムを例にとって、そのことについて説明しよう。
今回の Sphereに定義された変換は、Armの先端で$2$倍拡大するというものであった。プログラムでは Code3の1行目から3行目の部分で、実行手順は、まず原点において$2$拡大(sclSphere)、そして Armの先端(Arm座標系の $(5, 4, 0)$ )にアタッチ(traSphere)という順序である。この変換は結果的には、$(5, 4, 0)$だけ平行移動した地点において$2$倍拡大した状態になる。
そして肝心なことは、Sphereに定義された これらの変換は、Sphereの親座標系である Arm座標系の中で実行されるということである。図12に示されているように、Sphereは、Arm座標系の中で $2$倍に拡大し、Arm座標系の中で $(5, 4, 0)$に移動するのである。実際、他の座標系で見た場合、たとえば図11のワールド座標系では Sphereは$2$倍に拡大されてはいるが Sphereの(中心の)位置は $(5.5, 4.0, 1.33)$ であり、図13の Sphere座標系では Sphereの位置は原点から動いていない、さらに Sphere座標系における Sphereの半径の大きさ $1$のままである。つまり、ワールド座標系や Sphere座標系からでは Sphereに対して定義された「$(5, 4, 0)$だけ平行移動した地点において$2$倍拡大」という変換は見えないのである。
Armの場合も同様である。Armに定義された変換は、$(3, 0, -3)$ だけ移動し、その場所において Armの支点を通る軸mの周りに $-60$°回転するというものであった。プログラムでは Code3の5行目から7行目の部分で、実行手順は、まず原点においてy軸周りに $-60$°の回転(rotArm)、そして $(3, 0, -3)$ の平行移動(traArm)という順序である。Armは親オブジェクトを持たないので、前節で述べたように親座標系はワールド座標系になる。したがって、この2つの変換はワールド座標系の中で実行されることになる。
実際、図11では Armの支点が $(3, 0, -3)$ に移動しており、さらにその支点の周りに Armは $-60$°回転している(図を見ただけでは回転角度までは分からないが)。これらの変換は、Armの親座標系であるワールド座標系の中で起こっていることなのである。

何度か述べているように、オブジェクトにどのような変換を実行しても、オブジェクトは、自身のローカル座標系の中では位置、向き、大きさなどの状態は変化しない、言い換えれば、自身のローカル座標系の中では初期状態から変わらないのである。
ここで1つ問題。
Sphereが $2$倍に拡大したので、それに伴って Sphere座標系も $2$倍に拡大した。これを明らかにしたものが、以下の図である。


この図は前節でも使用したものだが、図15は、$2$倍拡大されたSphereを Armの先端から Armの支点に移動させて、Arm座標系のみを表示したときの様子で、図16は、図15の状態から Arm座標系を非表示にし、Sphere座標系のみを表示したときの様子である。図からわかるように、Sphere座標系が $2$倍拡大したことにより、グリッドの1マス1マスの大きさが、Arm座標系のものよりも $2$倍拡大されている。
一方、Armに対しては スケールを実行していないので Armは拡大も、縮小もしていない。したがって、Arm座標系も同様に拡大、縮小は行われていない。それは、Arm座標系と その親座標系であるワールド座標系のサイズが同じであることを意味する。「サイズが同じ」とは、ここでは座標系のグリッドの1マス1マスの大きさが同じであるという意味である。実際、本節の図4を見れば、Arm座標系のグリッドが、ワールド座標系のグリッドの一部とぴたりと重なっていることがわかるであろう。
Arm座標系とワールド座標系のサイズが同じであるため、Code3実行後では、ワールド座標系においても Sphereの半径は $2$である。
ここで、Armに対して Sphereと同じように $2$倍の拡大を実行したとしよう。具体的には、Code3では7行目が以下のように記述されているが、
Matrix4x4 localArm = traArm * rotArm;
Matrix4x4 sclArm = TH3DMath.GetScale4x4(2.0f); Matrix4x4 localArm = traArm * rotArm * sclArm;
では、もしCode3を このように変更したとき、Arm座標系における Sphereの半径、ワールド座標系における Sphereの半径は、それぞれいくつになるであろうか。
(次の事柄を考えれば、容易に答えは出る。Armを $2$倍に拡大すると、Arm座標系も $2$倍に拡大する。さらに、Armにアタッチされている Sphereも $2$倍に拡大する。)
# Code4
それでは、今までの運動を統合したプログラムを作成する。すなわち、Armを $(3,0,−3)$だけ移動させた状態で、Armの支点を通り、ワールド座標系のy軸に平行な軸(図6の軸m)の周りに Armを回転させる。そのとき、回転する Armの先端では、Sphereが拡大縮小をしている(倍率は $1$倍から $2$倍)。
[Code4] (実行結果 図17、図18、図19)
i_shmSphere += 1.0f; // 単振動計算で使われる角度 float scale = 0.5f * Mathf.Sin(i_shmSphere * Mathf.Deg2Rad) + 1.5f; // 1 -- 2 Matrix4x4 sclSphere = TH3DMath.GetScale4x4(scale); Matrix4x4 traSphere = TH3DMath.GetTranslation4x4(c_attachPos_Sphere); Matrix4x4 localSphere = traSphere * sclSphere; i_degArm -= 1.0f; // Armの回転角度 Matrix4x4 rotArm = TH3DMath.GetRotation4x4(i_degArm, Vector3.up); Matrix4x4 traArm = TH3DMath.GetTranslation4x4(3, 0, -3); Matrix4x4 localArm = traArm * rotArm; Matrix4x4 worldSphere = localArm * localSphere; Matrix4x4 worldArm = localArm; Sphere.SetMatrix(worldSphere); Arm.SetMatrix(worldArm);
前節のCode3と同様に、1行目の i_shmSphereは 2行目の単振動の計算で用いられる角度で、このプログラムでは毎フレーム $1$°ずつ増加する。また、この計算によって scaleは $1$から $2$の間を往復する。7行目の i_degArmは、Armの回転角度で、毎フレーム $1$°ずつ減少する。したがって、Armはワールド座標系において毎フレーム、反時計回りに $1$°ずつ回転する (これは 図17のように、Armを見下ろす位置で見た場合である。もし Armを見上げる位置で、つまり Armの下側から見た場合は Armの回転は時計回りである)。
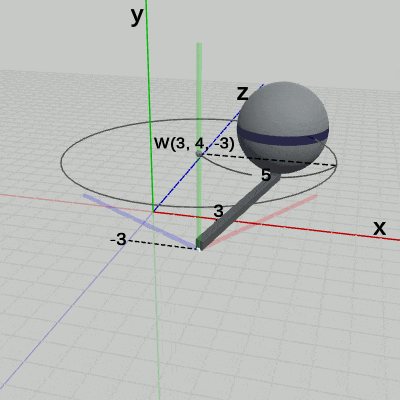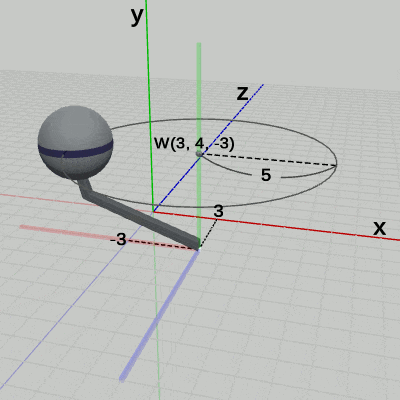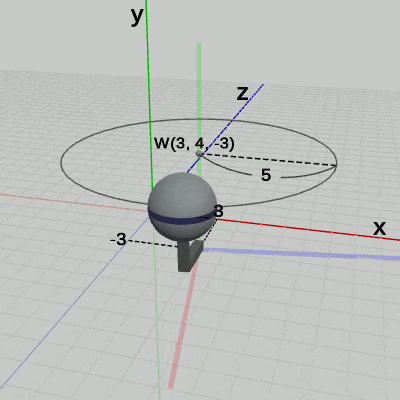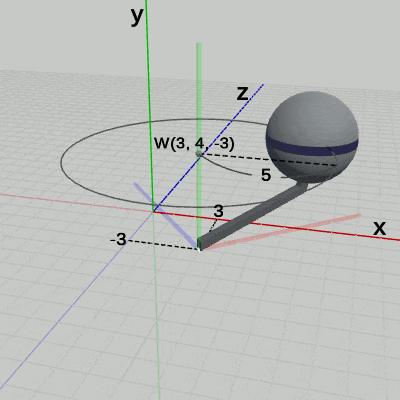 図17 Code4 実行結果 (ワールド座標系から見たときの様子)
図17 Code4 実行結果 (ワールド座標系から見たときの様子)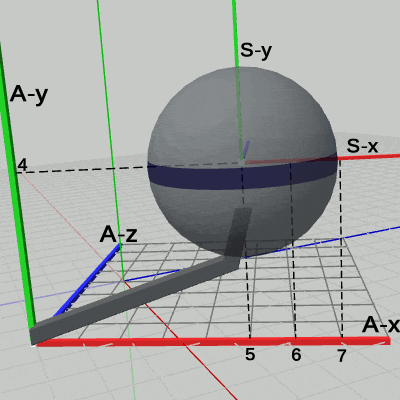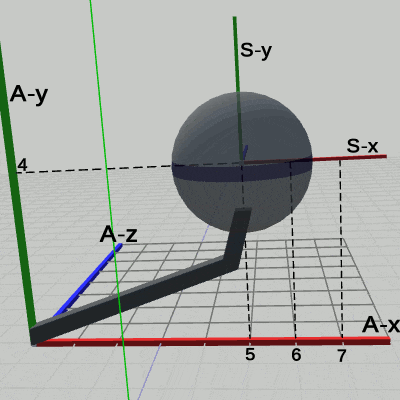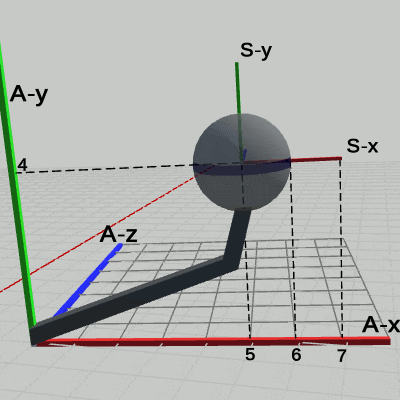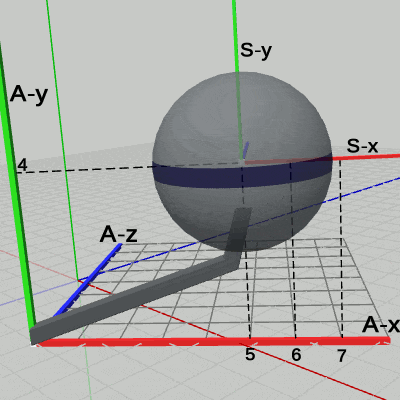 図18 Code4 実行結果 (Arm座標系から見たときの様子)
図18 Code4 実行結果 (Arm座標系から見たときの様子)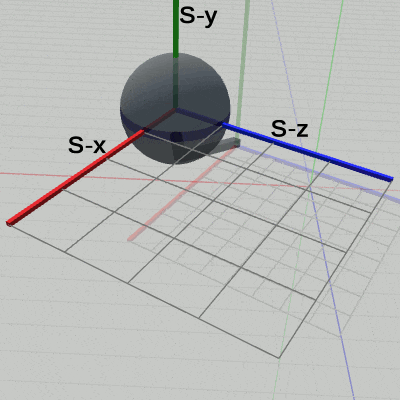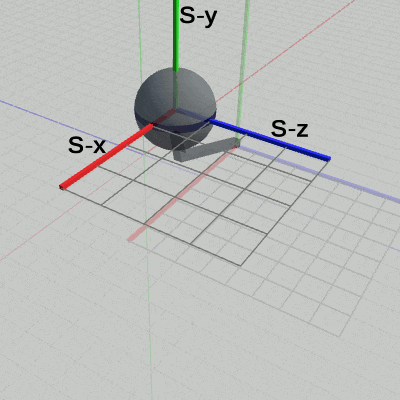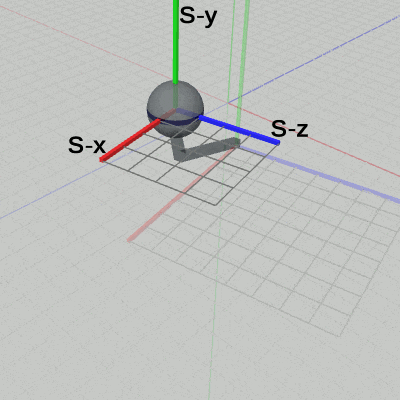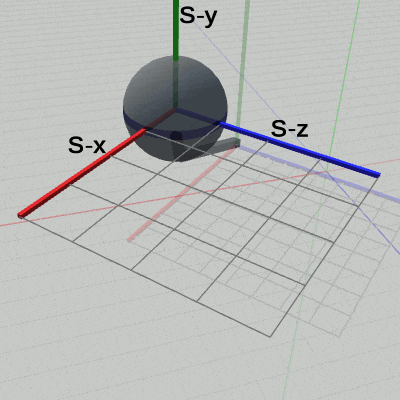 図19 Code4 実行結果 (Shpere座標系から見たときの様子)
図19 Code4 実行結果 (Shpere座標系から見たときの様子)
図17は、プログラムの実行結果をワールド座標系から見たときの様子である。Armは、$(3, 0, -3)$だけ平行移動し、その場所において、Armの支点周りに回転をしている。この $(3, 0, -3)$の平行移動と、支点周りの回転は、プログラムにおける7行目から10行目に記述されており、この2つの変換が Armに対して定義されている変換である。そして、これらの定義された変換は、Armの親座標系であるワールド座標系の中で実行されるのである。$(3, 0, -3)$だけ移動するのも、移動した場所において、支点周りに回転するのもワールド座標系の中で起こっていることである。言い換えれば、Armに対して定義されたこれらの変換の内容は、ワールド座標系の中で見えるのである。たとえば、図18の Arm座標系の中での Armは平行移動も回転もしていない。つまり、Arm座標系から見た場合は Armにどのような変換が定義されているかは見えないのである。
図18は、プログラムの実行結果を Arm座標系から見たときの様子である。周囲の風景が動いているが、Arm座標系における Armには何の変化も見られない (初期状態から変化しない ;「周囲の風景が動いている」という表現は、あまり適切ではない。実際には、図17に示されるように、Armの回転に伴って Arm座標系も回転している。その回転している Arm座標系にカメラを固定しているので、周囲の風景、つまりワールド座標系が動いているように見えるのである)。
Sphereは Arm座標系におけるアタッチポジションである $(5, 4, 0)$で、$1$倍から$2$倍の拡大縮小を繰り返している。この $(5, 4, 0)$の平行移動と、$1$倍から $2$倍の間の拡大縮小は、プログラムにおける1行目から5行目に記述されており、この2つの変換が Sphereに対して定義されている変換である。そして、これらの変換は、Sphereの親座標系である Arm座標系の中で実行されるのである。$(5, 4, 0)$だけ移動するのも、移動した場所において $1$倍から $2$倍の拡大縮小をするのも、Arm座標系の中で起こっている変換なのである。たとえば、図17に示されるように、ワールド座標系の中では、Sphereは、$(3, 4, -3)$を中心とする半径 $5$の円周上を拡大縮小しながら公転している。また、図19に示されるように、Sphere座標系の中では、Sphereは、常に中心が原点にある半径$1$の球(初期状態)のままである。つまり、ワールド座標系や Sphere座標系からでは、「$(5, 4, 0)$だけ移動して、その場所において$1$倍から $2$倍の拡大縮小をする」という変換は見えないのである。
図19は、プログラムの実行結果を Sphere座標系から見たときの様子である。Sphereは拡大縮小しているが、Sphere座標系も同じだけの拡大縮小をしているので、Sphere座標系の中では、Sphereの半径は常に $1$である。また、その位置は Sphere座標系の原点から動かない。つまり、Sphere座標系における Sphereは初期状態のままである。
© 2020-2025 Redpoll's 60 (All rights reserved)