Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-23
第4章 3D空間におけるオブジェクトの運動
$§$4-23 衝突判定 2
前節に引き続き以下の制約の下における3Dオブジェクト同士の衝突判定について見ていく。
前節では主にCannonから発射されたShellとオブジェクトとの衝突を扱ったが、本節では下図1のオブジェクトTankをXZ平面上で動かして、Tankと他のオブジェクトとの衝突を見ていく。
Tankの形状は直方体であり高さは $1.8$ で、上面及び底面は1辺の長さが $1$ の正方形であり、この正方形がTankの衝突モデルである。
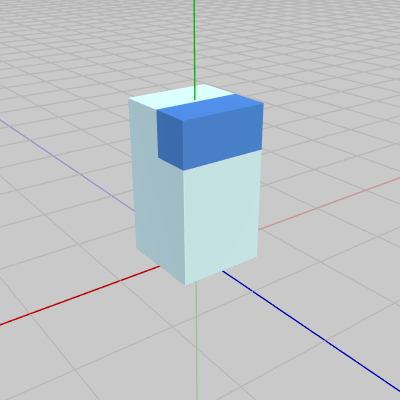
図1 Tank 初期状態 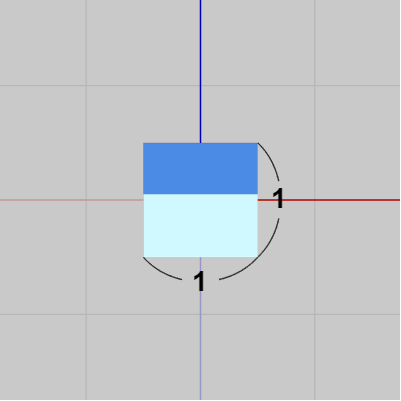
図2 Tankを真上から見ると1辺の長さが 1 の正方形
また前節と同様に本節で使用するオブジェクトもすべてカスタムライブラリーの THAlphaObject3D クラスのオブジェクトであり、このクラスには衝突判定のためのプロパティが用意されている。
例えば Tankの場合、各プロパティは次のように設定されている。
type は衝突モデルを表し、円盤か長方形のいずれかを指定する。width、height は衝突モデルが長方形である場合、その長方形のローカル座標系 x軸方向の長さ、z軸方向の長さである。
initRectVerts も衝突モデルが長方形である場合のみに使われ、これはオブジェクトの初期状態における長方形の各頂点座標のことであり、Tankの場合であれば図3の $P_0$~$P_3$ の座標がセットされている。initRectVerts は衝突判定をする際にその時点での衝突モデルの各頂点を計算するために使われるが、この点については後述する。

図3 Tank底面の各頂点 P0~P3 
図4 球の中心が高さ 0~1.8 の間にあれば衝突モデル同士が衝突する
また Tankは直方体であるのでXZ平面に平行な断面はすべて1辺が $1$ の正方形、すなわち Tankの衝突モデルと同じである。したがって、Tankの高さは $1.8$ であるから相手オブジェクトの衝突モデルの高さが $0$~$1.8$ の間にあれば、今回の方法で衝突判定を行うことが可能になる。例えば図4の球の場合はその中心の高さが $0$~$1.8$ の間にあればどこでも構わない。
本節ではプログラム実行中 次のキー操作によってTankを動かすが、その内容はメソッド UserMotion() として以下のように記述されている。
S : 前へ進む (Shiftと同時押しの場合は後ろへ進む)
H : Tankを反時計周り(左回り)に回転
L : Tankを時計周り(右周り)に回転
[UserMotion()]
最初のifブロックはリバウンド(跳ね返り処理)に関する部分であるが、この処理については後述する。
i_degTank (18、21行目)はTankの方向を変える際に用いる回転角度である (float型インスタンス変数)。H キーを押し続けるとTankは反時計周り(左回り)に回転し、L キーを押し続けるとTankは時計周り(右回り)に回転する。
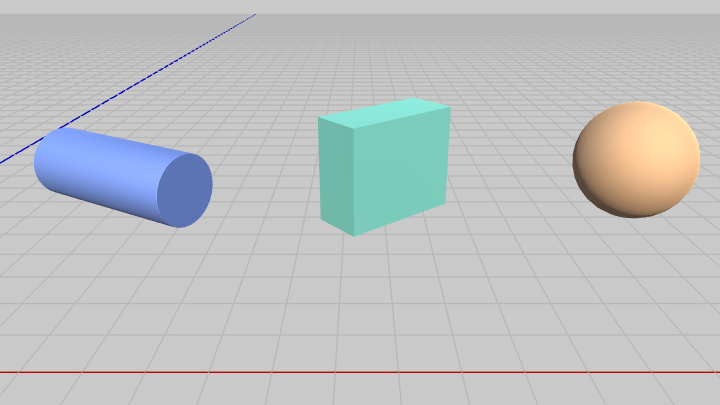
図6 Cylinder、Box、Sphere
各オブジェクトの衝突モデルを以下に示す。
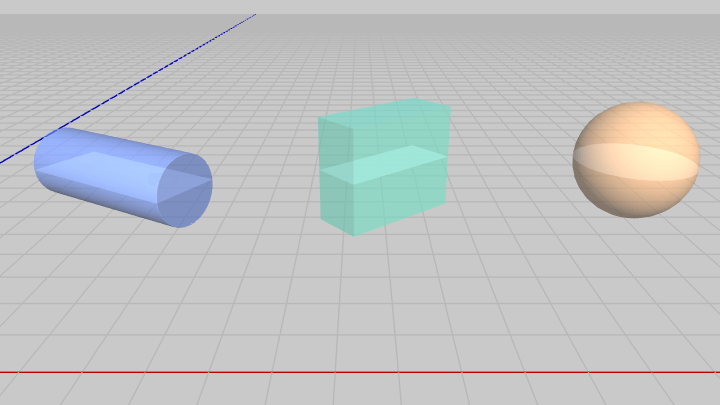
図7 各オブジェクトの衝突モデル
プログラムは次のとおり。
[Code1] (実行結果 図10)
初期化ブロックでは前節と同様に衝突対象のすべてのオブジェクトをインスタンス変数 i_targetObjects (THAlphaObject3D[]型)にセットしている。
13行目以降が衝突判定の部分であるが、その内容はTankが i_targetObjects にセットされたオブジェクトのいずれかと衝突しているかを調べるだけである。Tankの衝突モデルは長方形であるため相手オブジェクトとの衝突判定は「長方形 vs 円盤」あるいは「長方形 vs 長方形」のいずれかであり、前者であれば16行目、後者であれば23行目のifブロックに入る。
「長方形 vs 長方形」の衝突判定メソッド CollisionTest_Rect_Rect(..) (25行目)は名前は違っているがその内容は 2-21節の CollisionTest_OBB_OBB(..) と同じである。引数にはその時点における2つのオブジェクトの衝突モデルの頂点配列をセットするが、これはプログラムにあるように obj.rectVertsXZ とすればよい。
rectVertsXZ は THAlphaObject3D クラスのプロパティあり、その時点における長方形衝突モデルの頂点配列を取得するためのものである。例えば 今回のCylinderの場合であれば初期状態では下図8に示されるように横に寝かせた状態になっており2つの底面の中心を z軸が貫いている。衝突モデルは1辺の長さが $1$ の正方形であるがこれは円柱を2等分する断面であり、初期状態ではちょうどXZ平面に置かれている。
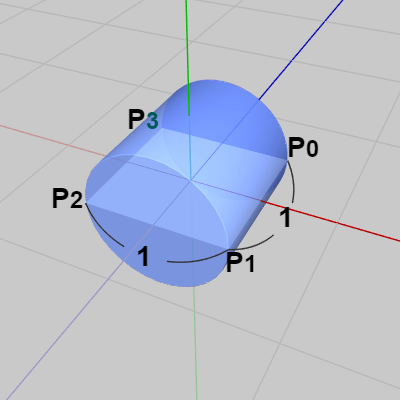
図8 Cylinder 初期状態 
図9 Cylinderに適当な変換を実行した状態
プログラム実行中のある時点においてCylinderが図9の状態になっていたとすると、このときのCylinderの rectVertsXZ は次のように計算される (最後のローカル変数 vertsXZ が rectVertsXZ の内容である)。
3~6行目の initRectVerts[0]~initRectVerts[3] はCylinderの初期状態における衝突モデルの頂点配列であり、具体的には上図8の $P_0$~$P_3$ のことである。同じく3~6行目の v[0]~v[3] は上図9におけるCylinderの衝突モデルの各頂点 $P_0$~$P_3$ のことである。衝突モデルとして長方形を使う場合には初期状態における頂点配置は、図8に示されるように $P_0$~$P_3$ を時計周りに配置する必要がある。
また 前節で述べたように衝突モデルの衝突判定はXZ平面上で行うことを前提としているが、実際にはXZ平面上ではなく衝突判定の計算はXY平面上で行われる。実際の rectVertsXZ の内容は上記のローカル変数 vertsXZ と同じものである (11行目)。

図10 Code1 実行結果 Tankといずれかのオブジェクトが衝突している場合には28行目のifブロックに入り、ローカル変数 collObj に衝突相手のオブジェクトをセットする。35行目の Collision(..) はこのローカル変数を引数に取るメソッドであるが、このメソッドは衝突が発生している際にTankと衝突相手のオブジェクトを赤く表示するための補助メソッドであり、引数の collObj がnullでない場合に両者が赤く表示される。
今回のプログラムではこのCoinを5枚適当な間隔で配置して衝突判定を行う。
プログラムは以下のとおり。
[Code2] (実行結果 図)
プログラム中では Coin は要素数 $5$ の配列であり、初期化ブロックにおいてそのまま i_targetObjects にセットされる。
このプログラムは13行目の UserMotion() 以降はCode1と同じであり、その内容もTankとCoinが衝突した場合にはTankの色を変え、衝突相手のCoinを消すだけである。
Coinと衝突するたびにCoinは消えていくが、R キーを押せば5枚のCoinはすべて元の位置に戻る。
衝突対象のオブジェクトの衝突モデルは円盤か長方形のいずれかであり、Tankは上から見た場合には正方形であるから実際には「正方形 vs 円盤」「正方形 vs 長方形」の2種類の場合だけを扱えばよい。
(1) 円盤の場合
円盤の場合は簡単である。
円盤の中心を $C$、正方形の中心を $S$ とするとき、衝突時のリバウンド方向は $C$ から $S$ の方向とする。
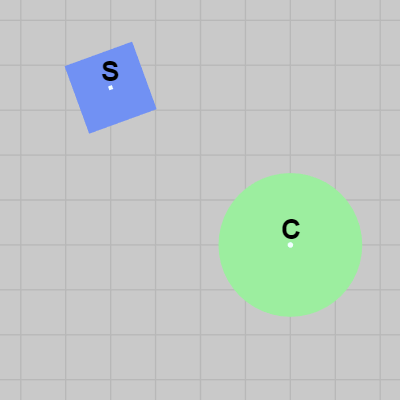
図14 正方形と円盤 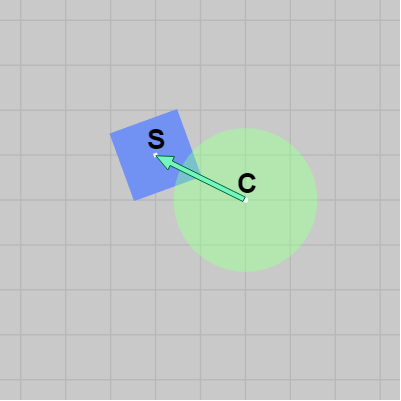
図15 衝突時のリバウンド方向は C から S の方向
(2) 長方形の場合
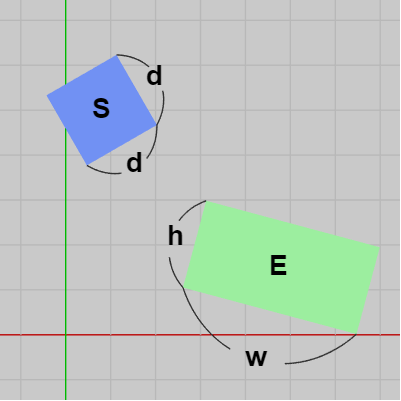
図16 正方形と長方形 (XY平面に置かれている) 以下においても正方形の中心を $S$ とし、正方形の1辺の長さを $d$ とする。また 長方形の中心を $E$、各辺の長さを $w$、$h$ とし(図16)、ここでは正方形及び長方形はXY平面に置かれているものとする。
下図17は長方形及びそのローカル座標系を表示したものであり、$\boldsymbol{lx}$、$\boldsymbol{ly}$ はローカル座標系の x軸、y軸を表すが、この図においては $\boldsymbol{lx}$、$\boldsymbol{ly}$ はXY平面上の x軸、y軸と重なっている (長方形の中心 $E$ は原点に位置している)。
図中には正方形も置かれているが、正方形の左下隅と長方形の右上隅の頂点が一致するように置かれている。正方形の各辺は長方形のローカル座標系の各軸に平行であり、正方形の中心 $S$ の位置は $(w/2 + d/2,\ h/2 + d/2)$ である。このとき 長方形のローカル座標系 x軸と線分 $ES$ のなす角を $A$ とする。
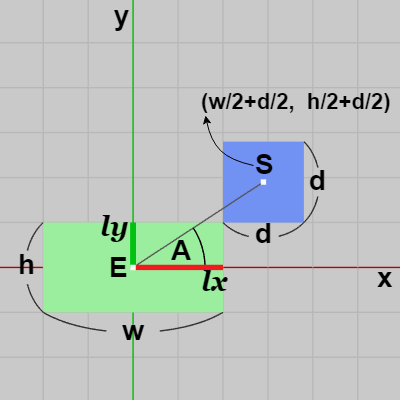
図17 第1象限でのなす角 A 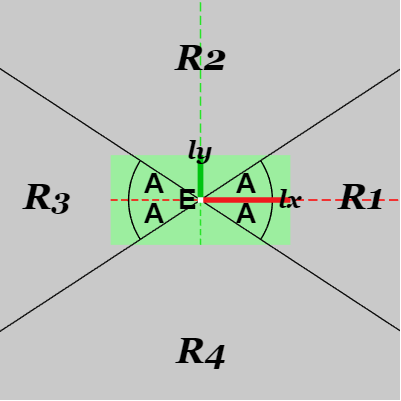
図18 長方形の周りは E を中心として4つの領域 R1~R4 に分割される
図17のなす角 $A$ はXY平面上の第1象限において定めたものであるが、第2~4象限においても同様の手続きによってなす角 $A$ を定めると図18に示されるように長方形の周りは4つの領域 $R1$~$R4$ に分割される。
正方形を長方形の周囲で適当に動かすとき、長方形と衝突した際の線分 $ES$ と長方形のローカル座標系 x軸のなす角を $B$ とする (下図19)。
このとき、正方形の中心 $S$ が上図18の4つの領域 $R1$~$R4$ のどの領域にあるかについては、以下の対応関係がある (以下では $E$ から $S$ の方向を表す単位ベクトルを $\boldsymbol{u}$ としている)。
(1) $-A \leq B \leq A $ であれば(正方形の中心) $S$ は $R1$ にある。
(2) $180-A\ \leq\ B\ \leq\ 180+A $ であれば $S$ は $R3$ にある。
(3) 上記のいずれでもないとき、$\boldsymbol{u}$ と $\boldsymbol{ly}$ の内積が $0$ 以上であれば $S$ は $R2$ にある ($A < B < 180-A $)。
(4) 上記のいずれでもないときは $S$ は $R4$ にある ($180+A < B < 360-A $)。
$\boldsymbol{u}\cdot\boldsymbol{lx} = \cos{B}$ であるから、上記の (1)、(2) は次のように書き換えられる。
(1) $\cos{A} \leq \cos{B} \leq 1$ であれば $S$ は $R1$ にある。
(2) $-1 \leq \cos{B} \leq -\cos{A}$ であれば $S$ は $R3$ にある。
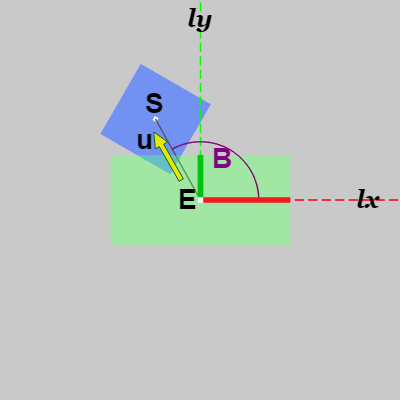
図19 角度 B はローカル座標系 x軸と線分ESのなす角 (u はEからSの方向を表す単位ベクトル) 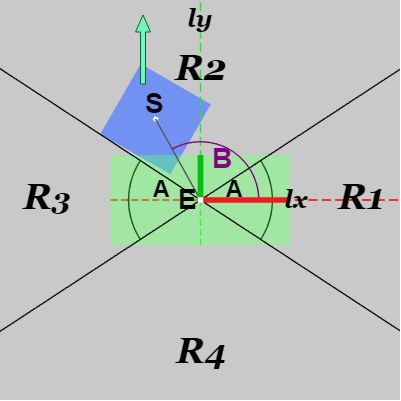
図20 この場合は S は領域R2にあるので ly 方向にリバウンド
以上をもとにして正方形と長方形が衝突した際のリバウンド方向を次のように定める。
(1) 衝突した際に、正方形の中心 $S$ が $R1$ にあれば、正方形のリバウンド方向を $\boldsymbol{lx}$ とする。
(2) $S$ が $R3$ にあれば、リバウンド方向を $-\boldsymbol{lx}$ とする。
(3) $S$ が $R2$ にあれば、リバウンド方向を $\boldsymbol{ly}$ とする。
(4) $S$ が $R4$ にあれば、リバウンド方向を $-\boldsymbol{ly}$ とする。
例えば上図の衝突例では図20に示されるように $S$ は領域 $R2$ にあるので、正方形のリバウンド方向は $\boldsymbol{ly}$ になる。
では今述べてきたことを実際のプログラムに実装しよう。
次のプログラムは正方形と長方形が衝突した際に上記のリバウンドが行われるようにしたものである。正方形及び長方形はXY平面上に置かれており(図21、図22)、プログラム中ではそれぞれ Square、Rect として使われている。
また Square(正方形)及びRect(長方形)は以下のキー操作によって動かすものとする。
S : Squareを青いマークのある方向に進ませる (Shiftと同時押しの場合は逆方向に進む)。
H : Squareを反時計周り(左回り)に回転。
L : Squareを時計周り(右周り)に回転。
R : Rectを反時計周りに回転 (Shiftと同時押しの場合は時計周りに回転)。
プログラムを以下に示す。
[Code3] (実行結果 図23)
初期化ブロックでは上の解説中で使われた $\cos{A}$ を算出している。このプログラムにおける長方形は $w=4$、$h=1.6$ で、正方形の1辺の長さは $1$ なので、上図17のように正方形を置いたときの正方形の中心 $S$ の位置は $(2+0.5,\ 0.8+0.5)$ となる。$E$ から $S$ の方向への単位ベクトルを $\boldsymbol{u}$ とし、長方形のローカル座標系の x軸を $\boldsymbol{lx}$ とすれば、$\boldsymbol{u}\cdot\boldsymbol{lx}=\cos{A}$ であるが、簡単のためここでは長方形のローカル座標系 x軸がXY平面の x軸に等しいと考えれば、$\boldsymbol{lx} = (1, 0)$ となるからこの内積は\[ \boldsymbol{u}\cdot\boldsymbol{lx} = \boldsymbol{u}\cdot (1, 0) = u_x = \cos{A}\]である (4行目)。
11行目の RectMotion() は長方形を回転させるためのものであり、ここでは R キーを押すことで長方形を回転させることができる。31~51行目は上記のプログラムにおける UserMotion() と内容は同じであり、ここでは H、L、S キーによって正方形を動かすための処理が記述されている。
54行目以降が衝突判定の部分である。54~56行目はSquareとRectが衝突しているかを調べるものであり、これは長方形同士の衝突判定メソッド CollisionTest_Rect_Rect(..) を使えばよい。GetVerts(..) は引数に指定されたオブジェクトのその時点での頂点配列を返す補助的なメソッドである。Squareであれば正方形であるから、その時点での正方形の各頂点座標が配列として返される。
衝突している場合には58行目のifブロックに入り、ここで正方形のリバウンド方向を算出する。その内容は上記の解説を実装しただけであり、使われている変数も上の解説のものと同じである。E は長方形の中心、lx、ly は長方形のローカル座標系の x軸、y軸を表す単位ベクトル、S は正方形の中心、u は E から S の方向を表す単位ベクトルである。
リバウンド方向はインスタンス変数 i_reboundDirection にセットされる。リバウンド方向に関して上図18で用いた4つの領域 $R1$~$R4$ で言い表せば、70行目のifブロックは正方形の中心 $S$ が $R1$ にある場合であり、74行目のelse ifブロックは $S$ が $R3$ にある場合、80行目、84行目の各ブロックは $S$ が $R2$、$R4$ にある場合である。
60行目の i_reboundCount はリバウンド処理を何フレーム行うかを表すint型インスタンス変数である。ここでは $4$ となっているが、これは正方形が長方形に衝突してから4フレームの間は i_reboundDirection の方向に正方形を移動させるということを意味している。
リバウンド処理は16行目のifブロックにおいて行われる。
ここでの処理は正方形を4フレームの間 i_reboundDirection の方向に $0.03$ ずつ移動させるだけである (正方形の向きは変化しない)。なお このifブロックの最後に return 文があるためリバウンド処理の間は正方形に対するキー操作は行えない。
今回のプログラムはXY平面上に置かれたオブジェクトの衝突判定であり、リバウンド方向の計算もXY平面上であることを前提としていた。しかし 4-24節までの衝突判定は今まで見てきたようにXZ平面上での衝突判定を前提としている。したがって 上記のリバウンド方向の計算を独立したメソッドとして、次のようにXZ平面上のものに書き改める。
[CalcReboundDirection(..)]
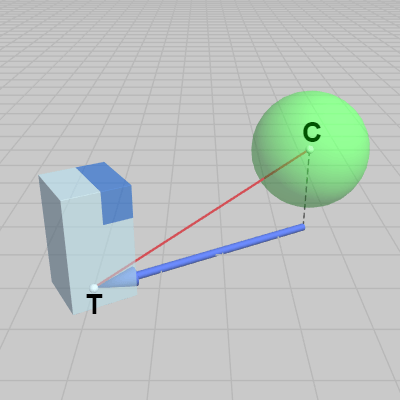
図24 相手オブジェクトからTankへの方向を表す青いベクトル (このベクトルはXZ平面に平行) このメソッドはTankの現在の位置と衝突相手のオブジェクトを引数に取る。メソッド冒頭において相手オブジェクトの位置からTankの位置までの方向をまず計算するが、ここで必要なのは真上から見下ろした場合における相手オブジェクトからTankへの方向であり、その方向はXZ平面に平行なベクトルでなければならない。
Tankの位置(posTank)や相手オブジェクトの位置(posTrg)はオブジェクト原点(ローカル座標系の原点)のことであるが、その高さは同じとは限らないので、相手オブジェクトの位置からTankの位置を結ぶベクトル vtr の高さ方向の成分を $0$ にして vtr がXZ平面に平行になるようにし、6行目でその単位ベクトル u を計算している。
8行目以降は上で見てきたものと同じである。ただし 今回はXZ平面上での計算であるため長方形のローカル座標系 x軸と z軸が使わている (プログラム中ではそれぞれ lx、lz)。
また プログラム中では THAlphaObject3D クラスの cosA というプロパティが使われているが、これは上の解説における $\cos{A}$ のことであり、このプロパティには事前に適切な値がセットされている。
プログラムを以下に示す。
[Code4]
Code1との違いは衝突した際に入る27行目のifブロックの内容が変わっている点である。reboundCount、reboundSpeed、reboundDirection はリバウンド処理のためのプロパティであり、リバウンド処理が行われるフレーム数、リバウンド時の毎フレーム の移動量、リバウンド方向を表す。ここではリバウンド処理は1フレームのみであり、そのフレームでは $0.08$ だけ移動するように設定している。
リバウンド方向は上で解説したメソッド CalcReboundDirection(..) によって計算する (33行目)。
Tankを動かすために毎フレーム UserMotion() (8行目)を実行するが、このメソッドの冒頭には次のようにリバウンド処理のためのifブロックが用意されている。
[UserMotion()]
リバウンド処理の内容は reboundCount が $0$ になるまでTankを reboundDirection の方向に毎フレーム reboundSpeed ずつ移動させるだけである。なお、このifブロックの最後には return 文があるため、リバウンド中はTankを動かすことはできない。
例えば下図に示される立体的な文字オブジェクトであっても真上から見下ろした場合に長方形であれば、今までと同じ方法で衝突判定を行うことができる。

図25 文字オブジェクト 
図26 左図のオブジェクトを真上から見下ろしたとき
今回はXZ平面上に並んだ複数の文字オブジェクト(図27)との衝突判定を行う。これらの文字はいずれも真上から見ると長方形であり、したがって衝突モデルはすべて長方形である。

図27 
図28 Code5 実行結果
プログラムを以下に示す。
[Code5] (実行結果 図28)
使用するオブジェクトが異なるだけでこのプログラムはCode4と同じである (今回はオブジェクトを動かさないので10行目の ObjectMotion() はコメントアウトしている)。初期化ブロックにおける Letter は5つの文字がセットされた配列である。
実行結果(図28)を見ると3Dオブジェクト同士の衝突判定が行われているように見えるが、実際には長方形と長方形の衝突判定である。
ここでは簡単な例でそれを示そう。以下のオブジェクト Chaser は今回使用するオブジェクトである。このオブジェクトは複数の部品で構成されているが全体の形状は球体であり、したがってその衝突モデルは円盤である。
このオブジェクトはプログラム実行中 常にTankに向かって突進して来る。そしてその突進はTankに衝突するまで続く。Chaserのスピードは最初は遅いが時間経過とともに次第にスピードアップするので、Tankも衝突されないようにするためにはより速く移動する必要がある。そのため、今回はTankのキー操作に加速が追加されている。
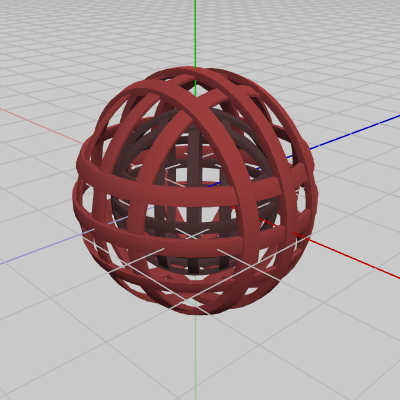
図29 Chaser 初期状態 (全体としては球体であるため衝突モデルは円盤) 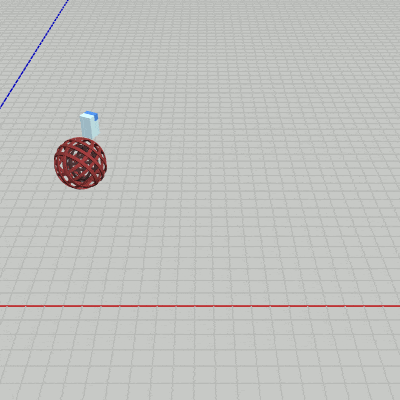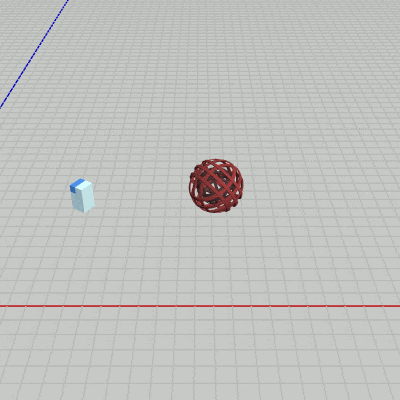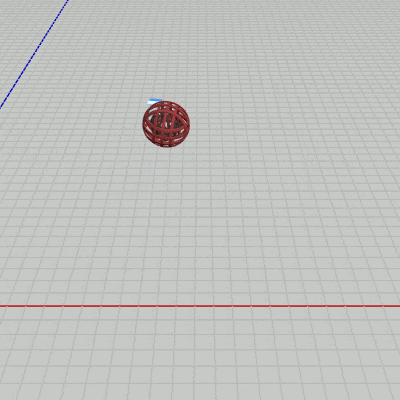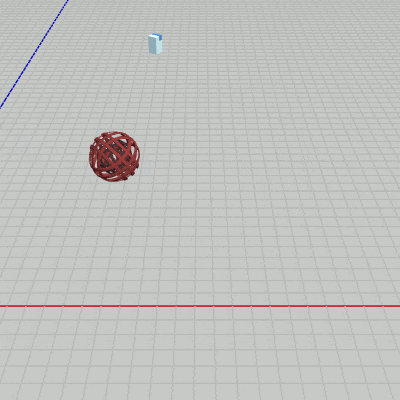
図30 Code6 実行結果
今回のキー操作は以下のとおり。
S : 前へ進む (Shiftと同時押しの場合は後ろへ進む)
H : Tankを反時計周りに回転
L : Tankを時計周りに回転
A : 前進するスピードを加速 (Shiftと同時押しの場合は減速)
V : Chaserが映るようにカメラを移動
プログラムは以下のとおり。
[Code6] (実行結果 図30)
プログラム自体はCode4やCode5と同じである。ただし衝突時に入る27行目のifブロックにおいて reboundCount、reboundSpeed の値が決まった値ではなく、相手オブジェクト Chaser のスピードに応じて変化するようなっており、Chaserのスピードが速ければ速いほど衝突時のTankに対する衝撃は大きくなる (29行目の GetChaserSpeed() はその時点におけるChaserの1フレームあたりの移動量を返すメソッド)。主な違いはこの点だけである。
Chaserのスピードがあまり速くない状態で衝突するとTankのリバウンド量もわずかであるが、Chaserのスピードが速い場合における衝突ではその衝突によってTankはかなり飛ばされることになる (衝突後は両者のスピードは最初の値に戻る)。
36行目の Hit(..) は引数にセットされたオブジェクトの色を変えるための補助メソッドであり、ここではTankとChaserが衝突した際にTankの色を一時的に赤くするために使われている。
なお今回のプログラムではカメラは常にTankを追跡する形で移動するが、その移動によってChaserが画面の外側に来てしまうことが起こる。そのような状況において V キーを押すとTankとChaserの両方が映るような位置にカメラが自動的に移動する (画面中央にTankとChaserが来るようにカメラが移動する)。
ここでは衝突相手のオブジェクトに対してリバウンド関連のデータを適当に設定して、オブジェクトを押しながら移動するといった処理を実装する。
図31は今回使用するオブジェクト Cube である。Cubeは立方体であり、初期状態においてはその中心が原点に置かれている。
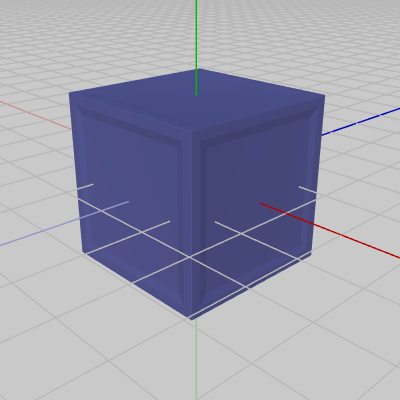
図31 Cube 初期状態 
図32 Code7 実行結果
プログラムは以下のとおり。
[Code7] (実行結果 図32)
基本的にはCode4~Code6と同じである。異なる点は衝突が発生した際にはリバウンド設定をTankに対してではなく、相手オブジェクトに対して行っていることである。具体的には37~41行目において、TankとCubeが衝突した場合には次のフレームにおいてCubeが $0.03$ だけリバウンドすることが設定されている。リバウンド方向はTankのリバウンド方向の逆方向がセットされる (41行目 ; CalcReboundDirection(..) にマイナスが付いているのはTankのリバウンド方向の逆方向にするためである)。
43~45行目は衝突時にTankの位置をわずかにずらすための調整的な処理である (ここでは進行方向とは逆の方向に $0.055$ だけ移動させる)。Tankにはリバウンド設定をしないので、今回は衝突後のTankはリバウンドをすることはない。この43~45行目の位置調整のみである。
10行目のifブロックはCubeのリバウンド処理であるが、その内容は UserMotion() におけるTankのリバウンド処理と同じである。
衝突時におけるこのようなリバウンド設定によって、実行結果(図32)に見られるようにTankがCubeを押しながら移動するようになる。
最後に、本節後半のプログラムにおいて使われた衝突判定処理を以下のように CollisionTest_ObjectPhase(..) というメソッドとして独立させる。
[CollisionTest_ObjectPhase(..)]
メソッド内の処理は本節のプログラム(特にCode4以降)で毎回使われていたものであり、特に新しい処理はない (メソッドの引数 target_arrahy はTankの衝突対象となるオブジェクトの配列)。
(1) オブジェクトが移動する際には水平方向(x軸、z軸方向)のみの移動とし、高さ方向(y軸方向)の移動は行わない。
(2) オブジェクトを配置する際には、オブジェクトの衝突モデルがXZ平面に平行になるように、さらに水平方向の移動によってオブジェクトの衝突モデル同士が必ず衝突するようにオブジェクトを配置する。
(2) オブジェクトを配置する際には、オブジェクトの衝突モデルがXZ平面に平行になるように、さらに水平方向の移動によってオブジェクトの衝突モデル同士が必ず衝突するようにオブジェクトを配置する。
前節では主にCannonから発射されたShellとオブジェクトとの衝突を扱ったが、本節では下図1のオブジェクトTankをXZ平面上で動かして、Tankと他のオブジェクトとの衝突を見ていく。
Tankの形状は直方体であり高さは $1.8$ で、上面及び底面は1辺の長さが $1$ の正方形であり、この正方形がTankの衝突モデルである。


また前節と同様に本節で使用するオブジェクトもすべてカスタムライブラリーの THAlphaObject3D クラスのオブジェクトであり、このクラスには衝突判定のためのプロパティが用意されている。
例えば Tankの場合、各プロパティは次のように設定されている。
Tank.type = c_RECT;
Tank.width = 1.0f;
Tank.height = 1.0f;
Tank.initRectVerts = new Vector3[]
{
new Vector3( 0.5f, 0.0f, 0.5f),
new Vector3( 0.5f, 0.0f, -0.5f),
new Vector3(-0.5f, 0.0f, -0.5f),
new Vector3(-0.5f, 0.0f, 0.5f)
};
type は衝突モデルを表し、円盤か長方形のいずれかを指定する。width、height は衝突モデルが長方形である場合、その長方形のローカル座標系 x軸方向の長さ、z軸方向の長さである。
initRectVerts も衝突モデルが長方形である場合のみに使われ、これはオブジェクトの初期状態における長方形の各頂点座標のことであり、Tankの場合であれば図3の $P_0$~$P_3$ の座標がセットされている。initRectVerts は衝突判定をする際にその時点での衝突モデルの各頂点を計算するために使われるが、この点については後述する。


また Tankは直方体であるのでXZ平面に平行な断面はすべて1辺が $1$ の正方形、すなわち Tankの衝突モデルと同じである。したがって、Tankの高さは $1.8$ であるから相手オブジェクトの衝突モデルの高さが $0$~$1.8$ の間にあれば、今回の方法で衝突判定を行うことが可能になる。例えば図4の球の場合はその中心の高さが $0$~$1.8$ の間にあればどこでも構わない。
本節ではプログラム実行中 次のキー操作によってTankを動かすが、その内容はメソッド UserMotion() として以下のように記述されている。
S : 前へ進む (Shiftと同時押しの場合は後ろへ進む)
H : Tankを反時計周り(左回り)に回転
L : Tankを時計周り(右周り)に回転
[UserMotion()]
if (Tank.reboundCount > 0)
{
Vector3 wp = Tank.GetWorldPosition() + Tank.reboundSpeed * Tank.reboundDirection;
Tank.SetWorldPosition(wp);
Tank.reboundCount--;
return;
}
bool MOVE = false;
if (Input.GetKey(KeyCode.S))
{
MOVE = true;
}
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
i_degTank += Input.GetKey(KeyCode.H) ? -3f : 3f;
}
Matrix4x4 R = TH3DMath.GetRotation4x4(i_degTank, Vector3.up);
Vector3 forwardDir = R * Vector3.forward;
float mv = MOVE ? 0.08f : 0.0f;
mv = THUtil.IsShiftDown() ? -mv : mv;
Vector3 pos = Tank.GetWorldPosition() + mv * forwardDir;
Matrix4x4 T = TH3DMath.GetTranslation4x4(pos);
Matrix4x4 M = T * R;
Tank.SetMatrix(M);
最初のifブロックはリバウンド(跳ね返り処理)に関する部分であるが、この処理については後述する。
i_degTank (18、21行目)はTankの方向を変える際に用いる回転角度である (float型インスタンス変数)。H キーを押し続けるとTankは反時計周り(左回り)に回転し、L キーを押し続けるとTankは時計周り(右回り)に回転する。
# Code1
まずは前節でも用いた以下の3つのオブジェクト Cylinder、Box、Sphere との衝突判定を行う。
各オブジェクトの衝突モデルを以下に示す。

プログラムは次のとおり。
[Code1] (実行結果 図10)
if (!i_INITIALIZED)
{
i_targetObjects = new THAlphaObject3D[] { Cylinder, Box, Sphere };
i_INITIALIZED = true;
}
UserMotion();
ObjectMotion();
THAlphaObject3D collObj = null;
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
collObj = target;
break;
}
}
Collision(collObj);
初期化ブロックでは前節と同様に衝突対象のすべてのオブジェクトをインスタンス変数 i_targetObjects (THAlphaObject3D[]型)にセットしている。
13行目以降が衝突判定の部分であるが、その内容はTankが i_targetObjects にセットされたオブジェクトのいずれかと衝突しているかを調べるだけである。Tankの衝突モデルは長方形であるため相手オブジェクトとの衝突判定は「長方形 vs 円盤」あるいは「長方形 vs 長方形」のいずれかであり、前者であれば16行目、後者であれば23行目のifブロックに入る。
「長方形 vs 長方形」の衝突判定メソッド CollisionTest_Rect_Rect(..) (25行目)は名前は違っているがその内容は 2-21節の CollisionTest_OBB_OBB(..) と同じである。引数にはその時点における2つのオブジェクトの衝突モデルの頂点配列をセットするが、これはプログラムにあるように obj.rectVertsXZ とすればよい。
rectVertsXZ は THAlphaObject3D クラスのプロパティあり、その時点における長方形衝突モデルの頂点配列を取得するためのものである。例えば 今回のCylinderの場合であれば初期状態では下図8に示されるように横に寝かせた状態になっており2つの底面の中心を z軸が貫いている。衝突モデルは1辺の長さが $1$ の正方形であるがこれは円柱を2等分する断面であり、初期状態ではちょうどXZ平面に置かれている。


プログラム実行中のある時点においてCylinderが図9の状態になっていたとすると、このときのCylinderの rectVertsXZ は次のように計算される (最後のローカル変数 vertsXZ が rectVertsXZ の内容である)。
Matrix4x4 M = Cylinder.GetMatrix();
v[0] = M * TH3DMath.ToVector4(Cylinder.initRectVerts[0]);
v[1] = M * TH3DMath.ToVector4(Cylinder.initRectVerts[1]);
v[2] = M * TH3DMath.ToVector4(Cylinder.initRectVerts[2]);
v[3] = M * TH3DMath.ToVector4(Cylinder.initRectVerts[3]);
Vector2[] vertsXZ = new Vector2[4];
for (int i = 0; i < 4; i++)
{
vertsXZ[i] = new Vector2(v[i].x, v[i].z);
}
3~6行目の initRectVerts[0]~initRectVerts[3] はCylinderの初期状態における衝突モデルの頂点配列であり、具体的には上図8の $P_0$~$P_3$ のことである。同じく3~6行目の v[0]~v[3] は上図9におけるCylinderの衝突モデルの各頂点 $P_0$~$P_3$ のことである。衝突モデルとして長方形を使う場合には初期状態における頂点配置は、図8に示されるように $P_0$~$P_3$ を時計周りに配置する必要がある。
また 前節で述べたように衝突モデルの衝突判定はXZ平面上で行うことを前提としているが、実際にはXZ平面上ではなく衝突判定の計算はXY平面上で行われる。実際の rectVertsXZ の内容は上記のローカル変数 vertsXZ と同じものである (11行目)。

# Code2
続いては下図11のオブジェクト Coin を対象として衝突判定を行う。Coinは初期状態では先程のCylinderと同じく円柱を横に寝かせた形状であり、2つの底面の中心を z軸が貫いている。図12はCoinの衝突モデルの長方形であるが、この長方形はCoinを2等分する断面である。-
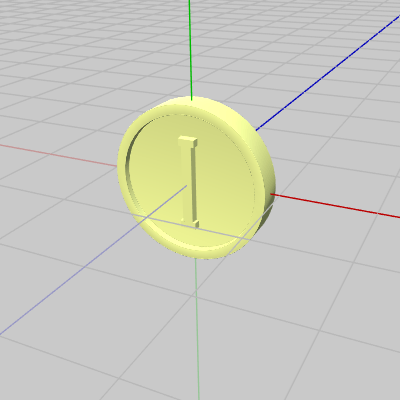 図11 Coin 初期状態
図11 Coin 初期状態 -
 図12 衝突モデルは長方形
図12 衝突モデルは長方形 -
 図13 Code2 実行結果
図13 Code2 実行結果
今回のプログラムではこのCoinを5枚適当な間隔で配置して衝突判定を行う。
プログラムは以下のとおり。
[Code2] (実行結果 図)
if (!i_INITIALIZED)
{
i_targetObjects = Coin; // Coin[0]--Coin[4]
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.R))
{
ResetCoins();
}
UserMotion();
ObjectMotion();
THAlphaObject3D collObj = null;
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
collObj = target;
break;
}
}
Collision(collObj);
プログラム中では Coin は要素数 $5$ の配列であり、初期化ブロックにおいてそのまま i_targetObjects にセットされる。
このプログラムは13行目の UserMotion() 以降はCode1と同じであり、その内容もTankとCoinが衝突した場合にはTankの色を変え、衝突相手のCoinを消すだけである。
Coinと衝突するたびにCoinは消えていくが、R キーを押せば5枚のCoinはすべて元の位置に戻る。
# Code3
ここではTankがオブジェクトに衝突した際のリバウンド処理(跳ね返り処理)について考える (具体的にここで考えるのはリバウンド方向である)。衝突対象のオブジェクトの衝突モデルは円盤か長方形のいずれかであり、Tankは上から見た場合には正方形であるから実際には「正方形 vs 円盤」「正方形 vs 長方形」の2種類の場合だけを扱えばよい。
(1) 円盤の場合
円盤の場合は簡単である。
円盤の中心を $C$、正方形の中心を $S$ とするとき、衝突時のリバウンド方向は $C$ から $S$ の方向とする。


(2) 長方形の場合

下図17は長方形及びそのローカル座標系を表示したものであり、$\boldsymbol{lx}$、$\boldsymbol{ly}$ はローカル座標系の x軸、y軸を表すが、この図においては $\boldsymbol{lx}$、$\boldsymbol{ly}$ はXY平面上の x軸、y軸と重なっている (長方形の中心 $E$ は原点に位置している)。
図中には正方形も置かれているが、正方形の左下隅と長方形の右上隅の頂点が一致するように置かれている。正方形の各辺は長方形のローカル座標系の各軸に平行であり、正方形の中心 $S$ の位置は $(w/2 + d/2,\ h/2 + d/2)$ である。このとき 長方形のローカル座標系 x軸と線分 $ES$ のなす角を $A$ とする。


図17のなす角 $A$ はXY平面上の第1象限において定めたものであるが、第2~4象限においても同様の手続きによってなす角 $A$ を定めると図18に示されるように長方形の周りは4つの領域 $R1$~$R4$ に分割される。
正方形を長方形の周囲で適当に動かすとき、長方形と衝突した際の線分 $ES$ と長方形のローカル座標系 x軸のなす角を $B$ とする (下図19)。
このとき、正方形の中心 $S$ が上図18の4つの領域 $R1$~$R4$ のどの領域にあるかについては、以下の対応関係がある (以下では $E$ から $S$ の方向を表す単位ベクトルを $\boldsymbol{u}$ としている)。
(1) $-A \leq B \leq A $ であれば(正方形の中心) $S$ は $R1$ にある。
(2) $180-A\ \leq\ B\ \leq\ 180+A $ であれば $S$ は $R3$ にある。
(3) 上記のいずれでもないとき、$\boldsymbol{u}$ と $\boldsymbol{ly}$ の内積が $0$ 以上であれば $S$ は $R2$ にある ($A < B < 180-A $)。
(4) 上記のいずれでもないときは $S$ は $R4$ にある ($180+A < B < 360-A $)。
$\boldsymbol{u}\cdot\boldsymbol{lx} = \cos{B}$ であるから、上記の (1)、(2) は次のように書き換えられる。
(1) $\cos{A} \leq \cos{B} \leq 1$ であれば $S$ は $R1$ にある。
(2) $-1 \leq \cos{B} \leq -\cos{A}$ であれば $S$ は $R3$ にある。


以上をもとにして正方形と長方形が衝突した際のリバウンド方向を次のように定める。
(1) 衝突した際に、正方形の中心 $S$ が $R1$ にあれば、正方形のリバウンド方向を $\boldsymbol{lx}$ とする。
(2) $S$ が $R3$ にあれば、リバウンド方向を $-\boldsymbol{lx}$ とする。
(3) $S$ が $R2$ にあれば、リバウンド方向を $\boldsymbol{ly}$ とする。
(4) $S$ が $R4$ にあれば、リバウンド方向を $-\boldsymbol{ly}$ とする。
例えば上図の衝突例では図20に示されるように $S$ は領域 $R2$ にあるので、正方形のリバウンド方向は $\boldsymbol{ly}$ になる。
では今述べてきたことを実際のプログラムに実装しよう。
次のプログラムは正方形と長方形が衝突した際に上記のリバウンドが行われるようにしたものである。正方形及び長方形はXY平面上に置かれており(図21、図22)、プログラム中ではそれぞれ Square、Rect として使われている。
-
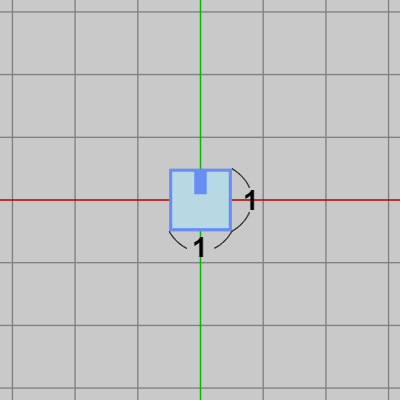 図21 Square 初期状態 (1 x 1 の正方形)
図21 Square 初期状態 (1 x 1 の正方形) -
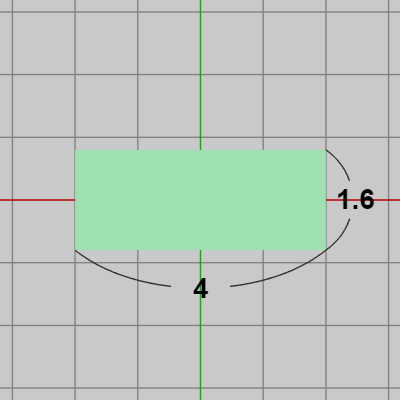 図22 Rect 初期状態 (4 x 1.6 の長方形)
図22 Rect 初期状態 (4 x 1.6 の長方形) -
 図23 Code3 実行結果
図23 Code3 実行結果
また Square(正方形)及びRect(長方形)は以下のキー操作によって動かすものとする。
S : Squareを青いマークのある方向に進ませる (Shiftと同時押しの場合は逆方向に進む)。
H : Squareを反時計周り(左回り)に回転。
L : Squareを時計周り(右周り)に回転。
R : Rectを反時計周りに回転 (Shiftと同時押しの場合は時計周りに回転)。
プログラムを以下に示す。
[Code3] (実行結果 図23)
if (!i_INITIALIZED)
{
Vector2 u = new Vector2(2.0f + 0.5f, 0.8f + 0.5f).normalized;
i_cosA = u.x;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.R))
{
RectMotion();
}
THMatrix3x3 M, T, R;
if (i_reboundCount > 0)
{
Vector2 wp = Square.GetPosition();
wp += 0.03f * i_reboundDirection;
R = TH2DMath.GetRotation3x3(i_degSquare);
T = TH2DMath.GetTranslation3x3(wp);
M = T * R;
Square.SetMatrix(M);
i_reboundCount--;
return;
}
bool MOVE = false;
if (Input.GetKey(KeyCode.S))
{
MOVE = true;
}
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.L))
{
i_degSquare += Input.GetKey(KeyCode.L) ? -2.5f : 2.5f;
}
R = TH2DMath.GetRotation3x3(i_degSquare);
Vector2 forwardDir = R * Vector2.up;
float mv = MOVE ? 0.05f : 0.0f;
mv = THUtil.IsShiftDown() ? -mv : mv;
Vector2 S = Square.GetPosition() + mv * forwardDir;
T = TH2DMath.GetTranslation3x3(S);
M = T * R;
Square.SetMatrix(M);
Vector2[] vertsA = GetVerts(Square);
Vector2[] vertsB = GetVerts(Rect);
bool bColl = CollisionTest_Rect_Rect(vertsA, vertsB);
if (bColl)
{
i_reboundCount = 4;
THMatrix3x3 mtx = Rect.GetMatrix();
Vector2 E = Rect.GetPosition();
Vector2 lx = mtx.GetColumn(0).normalized;
Vector2 ly = mtx.GetColumn(1).normalized;
Vector2 u = (S - E).normalized;
float cosB = Vector2.Dot(u, lx);
if (i_cosA <= cosB && cosB <= 1.0f)
{
i_reboundDirection = lx;
}
else if (-1.0f <= cosB && cosB <= -i_cosA)
{
i_reboundDirection = -lx;
}
else
{
if (Vector3.Dot(u, ly) >= 0.0f)
{
i_reboundDirection = ly;
}
else
{
i_reboundDirection = -ly;
}
}
}
初期化ブロックでは上の解説中で使われた $\cos{A}$ を算出している。このプログラムにおける長方形は $w=4$、$h=1.6$ で、正方形の1辺の長さは $1$ なので、上図17のように正方形を置いたときの正方形の中心 $S$ の位置は $(2+0.5,\ 0.8+0.5)$ となる。$E$ から $S$ の方向への単位ベクトルを $\boldsymbol{u}$ とし、長方形のローカル座標系の x軸を $\boldsymbol{lx}$ とすれば、$\boldsymbol{u}\cdot\boldsymbol{lx}=\cos{A}$ であるが、簡単のためここでは長方形のローカル座標系 x軸がXY平面の x軸に等しいと考えれば、$\boldsymbol{lx} = (1, 0)$ となるからこの内積は\[ \boldsymbol{u}\cdot\boldsymbol{lx} = \boldsymbol{u}\cdot (1, 0) = u_x = \cos{A}\]である (4行目)。
11行目の RectMotion() は長方形を回転させるためのものであり、ここでは R キーを押すことで長方形を回転させることができる。31~51行目は上記のプログラムにおける UserMotion() と内容は同じであり、ここでは H、L、S キーによって正方形を動かすための処理が記述されている。
54行目以降が衝突判定の部分である。54~56行目はSquareとRectが衝突しているかを調べるものであり、これは長方形同士の衝突判定メソッド CollisionTest_Rect_Rect(..) を使えばよい。GetVerts(..) は引数に指定されたオブジェクトのその時点での頂点配列を返す補助的なメソッドである。Squareであれば正方形であるから、その時点での正方形の各頂点座標が配列として返される。
衝突している場合には58行目のifブロックに入り、ここで正方形のリバウンド方向を算出する。その内容は上記の解説を実装しただけであり、使われている変数も上の解説のものと同じである。E は長方形の中心、lx、ly は長方形のローカル座標系の x軸、y軸を表す単位ベクトル、S は正方形の中心、u は E から S の方向を表す単位ベクトルである。
リバウンド方向はインスタンス変数 i_reboundDirection にセットされる。リバウンド方向に関して上図18で用いた4つの領域 $R1$~$R4$ で言い表せば、70行目のifブロックは正方形の中心 $S$ が $R1$ にある場合であり、74行目のelse ifブロックは $S$ が $R3$ にある場合、80行目、84行目の各ブロックは $S$ が $R2$、$R4$ にある場合である。
60行目の i_reboundCount はリバウンド処理を何フレーム行うかを表すint型インスタンス変数である。ここでは $4$ となっているが、これは正方形が長方形に衝突してから4フレームの間は i_reboundDirection の方向に正方形を移動させるということを意味している。
リバウンド処理は16行目のifブロックにおいて行われる。
ここでの処理は正方形を4フレームの間 i_reboundDirection の方向に $0.03$ ずつ移動させるだけである (正方形の向きは変化しない)。なお このifブロックの最後に return 文があるためリバウンド処理の間は正方形に対するキー操作は行えない。
今回のプログラムはXY平面上に置かれたオブジェクトの衝突判定であり、リバウンド方向の計算もXY平面上であることを前提としていた。しかし 4-24節までの衝突判定は今まで見てきたようにXZ平面上での衝突判定を前提としている。したがって 上記のリバウンド方向の計算を独立したメソッドとして、次のようにXZ平面上のものに書き改める。
[CalcReboundDirection(..)]
Vector3 CalcReboundDirection(Vector3 posTank, THAlphaObject3D target)
{
Vector3 posTrg = target.GetWorldPosition();
Vector3 vtr = posTank - posTrg;
vtr.y = 0.0f;
Vector3 u = vtr.normalized;
if (target.type == c_DISK)
{
return u;
}
else // c_RECT
{
Matrix4x4 M = target.GetMatrix();
Vector3 lx = M.GetColumn(0).normalized;
Vector3 lz = M.GetColumn(2).normalized;
float cosB = Vector3.Dot(u, lx);
if (target.cosA <= cosB && cosB <= 1.0f)
{
return lx;
}
else if (-1.0f <= cosB && cosB <= -target.cosA)
{
return -lx;
}
if (Vector3.Dot(u, lz) > 0.0f)
{
return lz;
}
return -lz;
}
}

Tankの位置(posTank)や相手オブジェクトの位置(posTrg)はオブジェクト原点(ローカル座標系の原点)のことであるが、その高さは同じとは限らないので、相手オブジェクトの位置からTankの位置を結ぶベクトル vtr の高さ方向の成分を $0$ にして vtr がXZ平面に平行になるようにし、6行目でその単位ベクトル u を計算している。
8行目以降は上で見てきたものと同じである。ただし 今回はXZ平面上での計算であるため長方形のローカル座標系 x軸と z軸が使わている (プログラム中ではそれぞれ lx、lz)。
また プログラム中では THAlphaObject3D クラスの cosA というプロパティが使われているが、これは上の解説における $\cos{A}$ のことであり、このプロパティには事前に適切な値がセットされている。
# Code4
Code1では3つのオブジェクト Cylinder、Box、Sphere との衝突判定を行ったが、そこではTankとオブジェクトの間で衝突が発生しても両者の色を変えるだけであった。今回は衝突した際の処理を上記のリバウンド処理に変更し、Tankとオブジェクトが衝突しても'めり込み'や'すり抜け'が起こらないようにしてみよう。プログラムを以下に示す。
[Code4]
if (!i_INITIALIZED)
{
i_targetObjects = new THSigmaObject3D[] { Cylinder, Box, Sphere };
i_INITIALIZED = true;
}
UserMotion();
ObjectMotion();
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
Tank.reboundCount = 1;
Tank.reboundSpeed = 0.08f;
Vector3 wp = Tank.GetWorldPosition();
Tank.reboundDirection = CalcReboundDirection(wp, target);
break;
}
}
Code1との違いは衝突した際に入る27行目のifブロックの内容が変わっている点である。reboundCount、reboundSpeed、reboundDirection はリバウンド処理のためのプロパティであり、リバウンド処理が行われるフレーム数、リバウンド時の毎フレーム の移動量、リバウンド方向を表す。ここではリバウンド処理は1フレームのみであり、そのフレームでは $0.08$ だけ移動するように設定している。
リバウンド方向は上で解説したメソッド CalcReboundDirection(..) によって計算する (33行目)。
Tankを動かすために毎フレーム UserMotion() (8行目)を実行するが、このメソッドの冒頭には次のようにリバウンド処理のためのifブロックが用意されている。
[UserMotion()]
void UserMotion()
{
if (Tank.reboundCount > 0)
{
Vector3 wp = Tank.GetWorldPosition() + Tank.reboundSpeed * Tank.reboundDirection;
Tank.SetWorldPosition(wp);
Tank.reboundCount--;
return;
}
...
...
}
リバウンド処理の内容は reboundCount が $0$ になるまでTankを reboundDirection の方向に毎フレーム reboundSpeed ずつ移動させるだけである。なお、このifブロックの最後には return 文があるため、リバウンド中はTankを動かすことはできない。
# Code5
今回行っている衝突判定は3Dオブジェクトの衝突モデルを利用して実際には衝突判定を平面上で行うものである。したがって、オブジェクトの衝突モデルが長方形や円盤であれば(すなわち 真上から見下ろした場合に長方形や円盤であれば)、その形状が単純なものでなくても今回の方法で衝突判定ができる。例えば下図に示される立体的な文字オブジェクトであっても真上から見下ろした場合に長方形であれば、今までと同じ方法で衝突判定を行うことができる。


今回はXZ平面上に並んだ複数の文字オブジェクト(図27)との衝突判定を行う。これらの文字はいずれも真上から見ると長方形であり、したがって衝突モデルはすべて長方形である。


プログラムを以下に示す。
[Code5] (実行結果 図28)
if (!i_INITIALIZED)
{
i_targetObjects = Letter; // Letter[0]--Letter[4]
i_INITIALIZED = true;
}
UserMotion();
// ObjectMotion();
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
Tank.reboundCount = 1;
Tank.reboundSpeed = 0.08f;
Vector3 wp = Tank.GetWorldPosition();
Tank.reboundDirection = CalcReboundDirection(wp, target);
break;
}
}
使用するオブジェクトが異なるだけでこのプログラムはCode4と同じである (今回はオブジェクトを動かさないので10行目の ObjectMotion() はコメントアウトしている)。初期化ブロックにおける Letter は5つの文字がセットされた配列である。
実行結果(図28)を見ると3Dオブジェクト同士の衝突判定が行われているように見えるが、実際には長方形と長方形の衝突判定である。
# Code6
リバウンド処理が行われるフレーム数を表すプロパティ reboundCount、及びリバウンド時における毎フレームの移動量を表すプロパティ reboundSpeed を調整することによって、衝突時の衝撃を表現することができる。ここでは簡単な例でそれを示そう。以下のオブジェクト Chaser は今回使用するオブジェクトである。このオブジェクトは複数の部品で構成されているが全体の形状は球体であり、したがってその衝突モデルは円盤である。
このオブジェクトはプログラム実行中 常にTankに向かって突進して来る。そしてその突進はTankに衝突するまで続く。Chaserのスピードは最初は遅いが時間経過とともに次第にスピードアップするので、Tankも衝突されないようにするためにはより速く移動する必要がある。そのため、今回はTankのキー操作に加速が追加されている。


今回のキー操作は以下のとおり。
S : 前へ進む (Shiftと同時押しの場合は後ろへ進む)
H : Tankを反時計周りに回転
L : Tankを時計周りに回転
A : 前進するスピードを加速 (Shiftと同時押しの場合は減速)
V : Chaserが映るようにカメラを移動
プログラムは以下のとおり。
[Code6] (実行結果 図30)
if (!i_INITIALIZED)
{
i_targetObjects = new THAlphaObject3D[] { Chaser };
i_INITIALIZED = true;
}
UserMotion();
ObjectMotion();
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
float speed = GetChaserSpeed();
Tank.reboundCount = (speed < 0.14f) ? 12 : (int)(speed * 125);
Tank.reboundSpeed = (speed < 0.14f) ? 0.084f : speed * 3.5f;
Vector3 wp = Tank.GetWorldPosition();
Tank.reboundDirection = CalcReboundDirection(wp, target);
Hit(Tank);
break;
}
}
プログラム自体はCode4やCode5と同じである。ただし衝突時に入る27行目のifブロックにおいて reboundCount、reboundSpeed の値が決まった値ではなく、相手オブジェクト Chaser のスピードに応じて変化するようなっており、Chaserのスピードが速ければ速いほど衝突時のTankに対する衝撃は大きくなる (29行目の GetChaserSpeed() はその時点におけるChaserの1フレームあたりの移動量を返すメソッド)。主な違いはこの点だけである。
Chaserのスピードがあまり速くない状態で衝突するとTankのリバウンド量もわずかであるが、Chaserのスピードが速い場合における衝突ではその衝突によってTankはかなり飛ばされることになる (衝突後は両者のスピードは最初の値に戻る)。
36行目の Hit(..) は引数にセットされたオブジェクトの色を変えるための補助メソッドであり、ここではTankとChaserが衝突した際にTankの色を一時的に赤くするために使われている。
なお今回のプログラムではカメラは常にTankを追跡する形で移動するが、その移動によってChaserが画面の外側に来てしまうことが起こる。そのような状況において V キーを押すとTankとChaserの両方が映るような位置にカメラが自動的に移動する (画面中央にTankとChaserが来るようにカメラが移動する)。
# Code7
今までのプログラムでは衝突時のリバウンドはTankのみに生じるものであり、相手側のオブジェクトはその衝突によって位置が変化することはなかった。ここでは衝突相手のオブジェクトに対してリバウンド関連のデータを適当に設定して、オブジェクトを押しながら移動するといった処理を実装する。
図31は今回使用するオブジェクト Cube である。Cubeは立方体であり、初期状態においてはその中心が原点に置かれている。


プログラムは以下のとおり。
[Code7] (実行結果 図32)
if (!i_INITIALIZED)
{
i_targetObjects = new THAlphaObject3D[] { Cube };
i_INITIALIZED = true;
}
UserMotion();
if (Cube.reboundCount > 0)
{
Vector3 posCube = Cube.GetWorldPosition() + Cube.reboundSpeed * Cube.reboundDirection;
Cube.SetWorldPosition(posCube);
Cube.reboundCount--;
}
foreach (var target in i_targetObjects)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
target.reboundCount = 1;
target.reboundSpeed = 0.03f;
Vector3 posTank = Tank.GetWorldPosition();
target.reboundDirection = -CalcReboundDirection(posTank, target);
Vector3 forwardDir = Tank.GetMatrix().GetColumn(2);
posTank -= 0.055f * forwardDir;
Tank.SetWorldPosition(posTank);
break;
}
}
基本的にはCode4~Code6と同じである。異なる点は衝突が発生した際にはリバウンド設定をTankに対してではなく、相手オブジェクトに対して行っていることである。具体的には37~41行目において、TankとCubeが衝突した場合には次のフレームにおいてCubeが $0.03$ だけリバウンドすることが設定されている。リバウンド方向はTankのリバウンド方向の逆方向がセットされる (41行目 ; CalcReboundDirection(..) にマイナスが付いているのはTankのリバウンド方向の逆方向にするためである)。
43~45行目は衝突時にTankの位置をわずかにずらすための調整的な処理である (ここでは進行方向とは逆の方向に $0.055$ だけ移動させる)。Tankにはリバウンド設定をしないので、今回は衝突後のTankはリバウンドをすることはない。この43~45行目の位置調整のみである。
10行目のifブロックはCubeのリバウンド処理であるが、その内容は UserMotion() におけるTankのリバウンド処理と同じである。
衝突時におけるこのようなリバウンド設定によって、実行結果(図32)に見られるようにTankがCubeを押しながら移動するようになる。
最後に、本節後半のプログラムにおいて使われた衝突判定処理を以下のように CollisionTest_ObjectPhase(..) というメソッドとして独立させる。
[CollisionTest_ObjectPhase(..)]
void CollisionTest_ObjectPhase(THAlphaObject3D[] target_arrahy)
{
foreach(var target in target_arrahy)
{
bool bColl = false;
if (target.type == c_DISK)
{
Vector2 lx = Tank.localAxisXZ[0];
Vector2 lz = Tank.localAxisXZ[1];
bColl = CollisionTest_Disk_Rect(target.positionXZ, target.radius,
Tank.positionXZ, Tank.width, Tank.height, lx, lz);
}
else if (target.type == c_RECT)
{
bColl = CollisionTest_Rect_Rect(Tank.rectVertsXZ, target.rectVertsXZ);
}
if (bColl)
{
Tank.reboundCount = 8;
Tank.reboundSpeed = 0.25f;
Vector3 posTank = Tank.GetWorldPosition();
Tank.reboundDirection = CalcReboundDirection(posTank, target);
Hit(Tank);
break;
}
}
}
メソッド内の処理は本節のプログラム(特にCode4以降)で毎回使われていたものであり、特に新しい処理はない (メソッドの引数 target_arrahy はTankの衝突対象となるオブジェクトの配列)。
© 2020-2025 Redpoll's 60 (All rights reserved)