Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-7
第4章 3D空間におけるオブジェクトの運動
$§$4-7 変換行列の計算
今までのプログラムでは、複数のオブジェクトを一体化させる処理はどのプログラムにおいても次のような形で記述されていた。
以前にも述べたがこの一体化運動の計算は実際には明らかに無駄な計算が含まれている。例えば1~3行目は以下のようにする方が効率的である。
一体化運動の行列計算は確かにこの部分に関しては簡単に効率化ができるが、より根本的に一体化運動の計算を効率化するためにはさらにいくつかの準備が必要になるため、その解説については第5章でまとめて行う。
一方で単一のオブジェクトに実行する変換行列の計算は、一部の例外を除き今までのプログラムでは以下のように行われていた。
つまりスケール、回転、平行移動の順になるように3つの変換行列の積を計算していたわけである。
しかし最終的にオブジェクトに対して実行する5行目の変換行列 $M$ は、実際のプログラムにおいて行列の積として求める必要はない。$M$ はスケール行列 $S$、回転行列 $R$、平行移動行列 $T$ をこの順番で掛けたものである。4-5節で述べたように $T$、$R$、$S$ を
この計算結果からわかるように、$M$ の1列目は $R$ の1列目に $s_x$ を掛けたもの、$M$ の2列目は $R$ の2列目に $s_y$ を掛けたもの、$M$ の3列目は $R$ の3列目に $s_z$ を掛けたものであり、$M$ の4列目は $T$ の4列目と同じである。
したがって単一のオブジェクトの場合、その変換行列は $M = TRS$ のように3つの行列の積を計算するのではなく、回転行列 $R$ をもとにして次のように直接'作る'ことができるのである。もちろん3つの行列の積を計算するよりは明らかに効率的である (以下の r[i, j] は解説中の $r_{ij}$ と同じである)。
では単一のオブジェクトの行列計算に使われるスケール成分 $(s_x, s_y, s_z)$、回転成分 $(r_{00}, r_{10}, r_{20})$、$(r_{01}, r_{11}, r_{21})$、$(r_{02}, r_{12}, r_{22})$、平行移動成分 $(t_x, t_y, t_z)$ を個別に変化させるとオブジェクトはどのように変化するのであろうか。
以下簡単な例を通して実際に見ていこう。
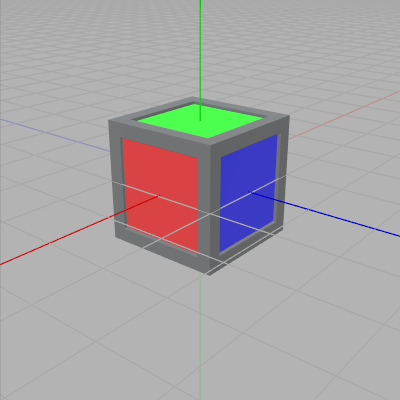
図1 Cube 初期状態 
図2 適当な変換を実行したとき
図1はオブジェクト Cube の初期状態である。Cubeは初期状態では立方体であり、その中心が原点に置かれている。図2はCubeに対し適当なスケール、回転、平行移動をこの順で行ったときのものであるが、このときのスケール成分を $(s_x, s_y, s_z)$、平行移動成分 $(t_x, t_y, t_z)$ で表し、Cubeに実行されている回転行列を小文字の $\large\boldsymbol{\mathsf{r}}$ で表す。
便宜上、プログラムにおける変換行列の計算には CalcMatrix(..) という以下のメソッドを使用する (上のコードをメソッド化したものである)。
まず図2の状態から平行移動成分 $(t_x, t_y, t_z)$ だけを変化させる場合である (X、Y、Z の各キーを押すことで $t_x$、$t_y$、$t_z$ が個別に変化する)。
下図に示されるように $t_x$ を変化させるとCubeのオブジェクト原点が、オブジェクト原点を通る x軸に平行な直線上を移動することになる。$t_y$ を変化させるとオブジェクト原点を通る y軸に平行な直線上を移動することになる。
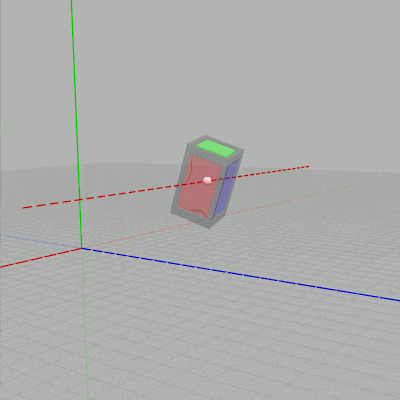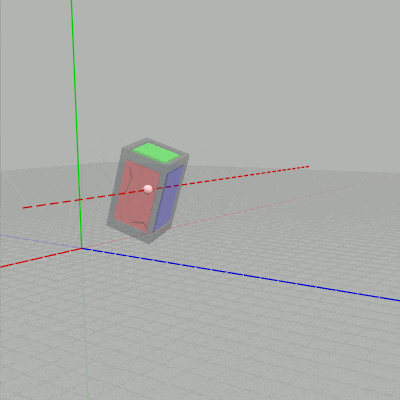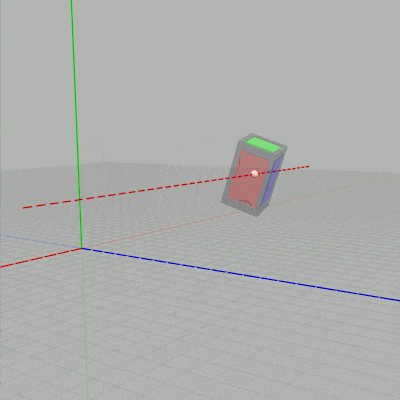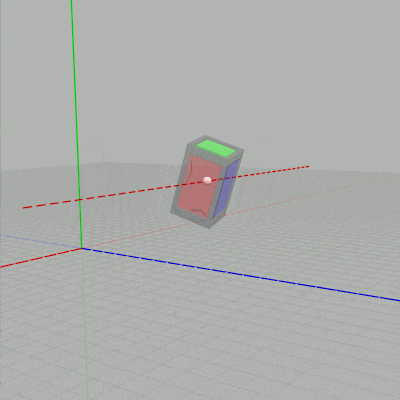
図3 $t_x$ を変化させる場合 (赤い点線は x軸に平行) 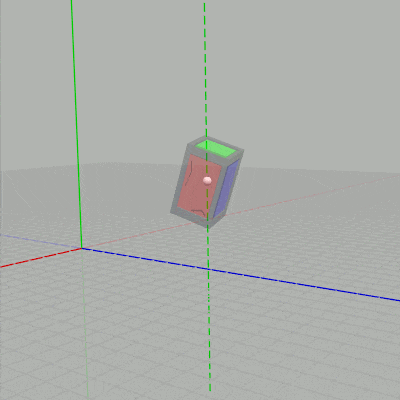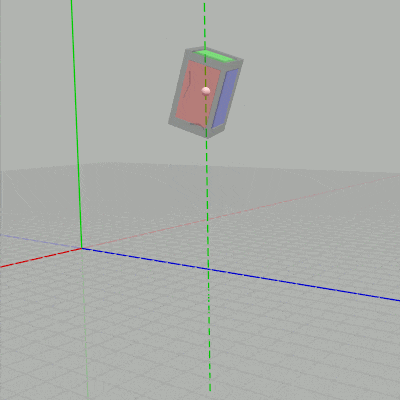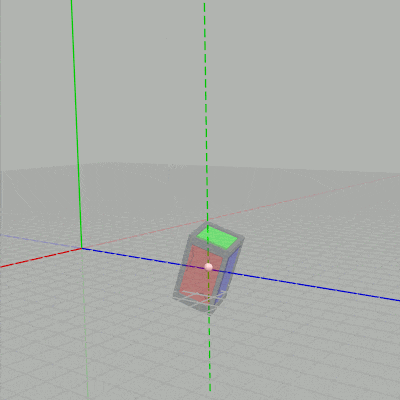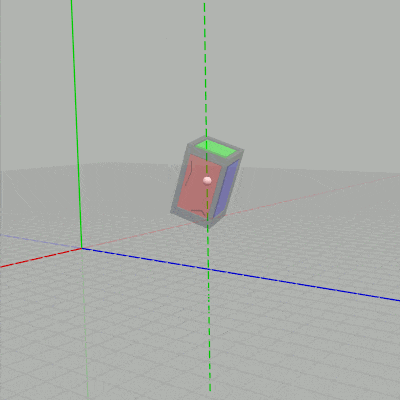
図4 $t_y$ を変化させる場合 (緑の点線は y軸に平行)
続いては図2の状態からスケール成分 $(s_x, s_y, s_z)$ だけを変化させる場合である (X、Y、Z の各キーを押すことで $s_x$、$s_y$、$s_z$ が個別に変化する)。
$s_y$ だけを変化させると下左図に示されるように、Cubeがローカル座標系の y軸に沿って拡大縮小する (ローカル座標系については次節で解説する)。$s_z$ だけを変化させると下右図に示されるように、Cubeがローカル座標系の z軸に沿って拡大縮小する。
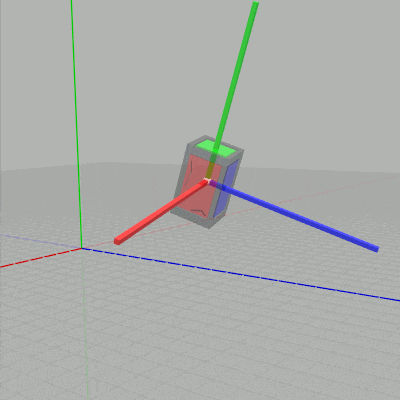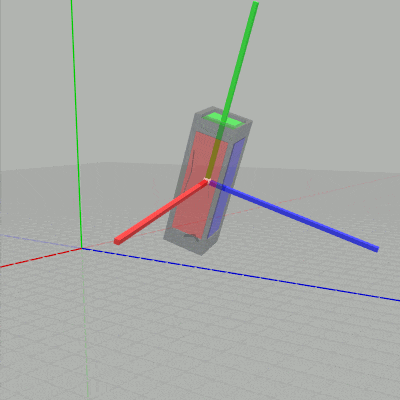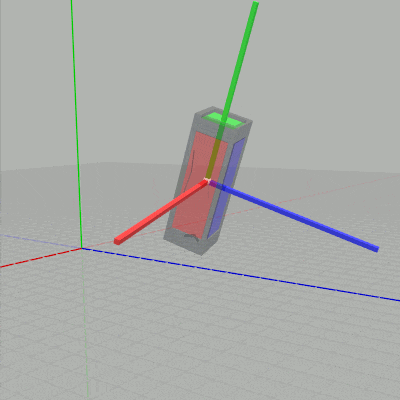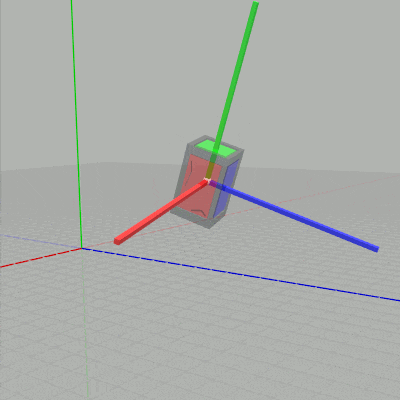
図5 $s_y$ を変化させる場合 (ローカル座標系の y軸に沿って拡大縮小) 
図6 $s_z$ を変化させる場合 (ローカル座標系の z軸に沿って拡大縮小)
続いては図2の状態のCubeに対し x軸周り、y軸周り、z軸周りの回転行列を個別に実行する。下のコードにおいて r は現在の回転状態を表す回転行列であり、Rx、Ry、Rz は x軸、y軸、z軸周りの回転を表す回転行列である (回転角度は $\pm 10^\circ$ )。
X キーが押されると図2の状態から下左図の赤い点線を回転軸として、$10^\circ$ あるいは $-10^\circ$ ずつ回転する (赤い点線はオブジェクト原点を通る x軸に平行な直線)。Y キーが押されると図2の状態から下右図の緑の点線を回転軸として、$10^\circ$ あるいは $-10^\circ$ ずつ回転する (緑の点線はオブジェクト原点を通る y軸に平行な直線)。
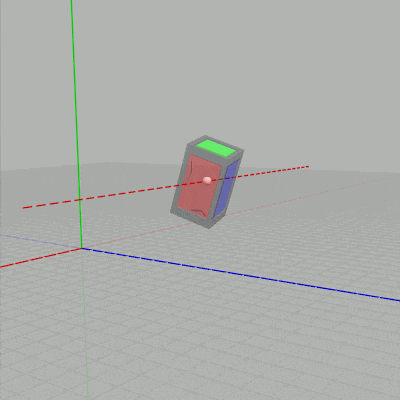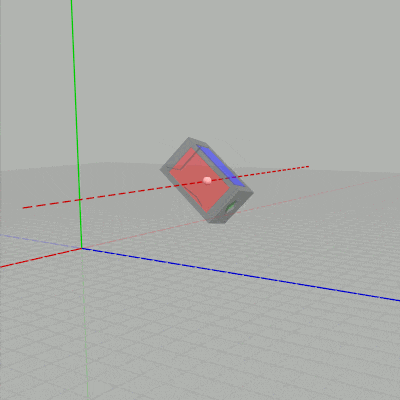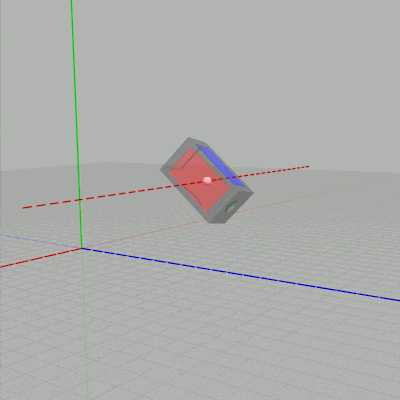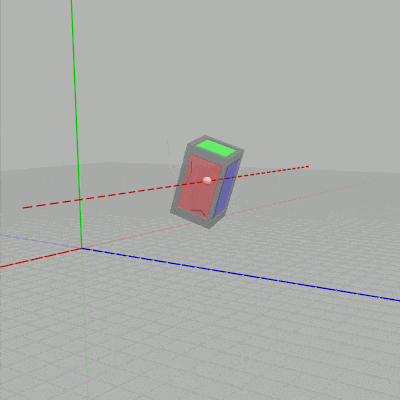
図7 赤い点線は x軸に平行 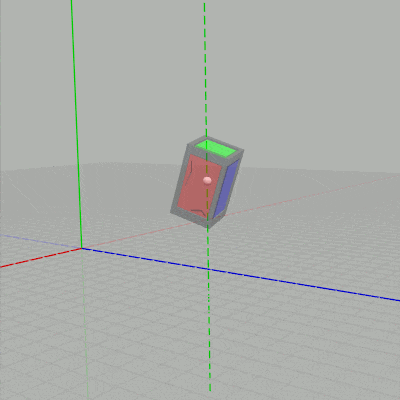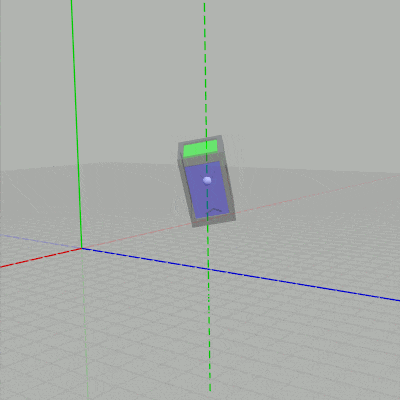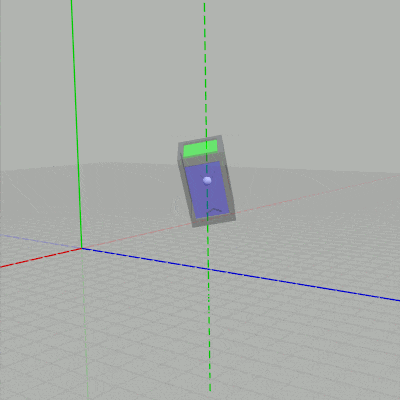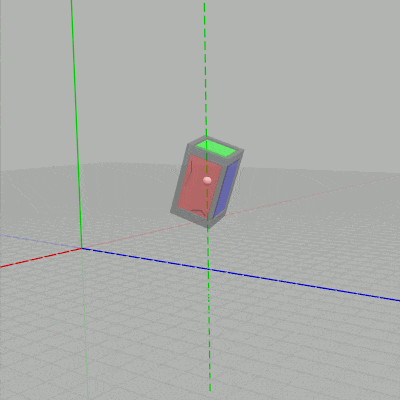
図8 緑の点線は y軸に平行
つまり変換行列の回転成分に対し x軸周り、y軸周り、z軸周りの回転行列を掛けるとオブジェクトは、自身のオブジェクト原点を通り x軸、y軸、z軸に平行な軸の周りに回転するのである。
列優先の場合には新しい行列を左に掛けていくので、現在の状態からさらに回転させるために上のコードでは回転行列 Rx、Ry、Rz を左に掛けたわけである。もしこれらの回転行列を左ではなく右に掛けると、すなわち上記コードの6~8行目を次のように変更すると下図に示されるようにオブジェクトのローカル座標系の軸周りの回転になる (ローカル座標系の軸周りの回転については6-3節で解説する)。
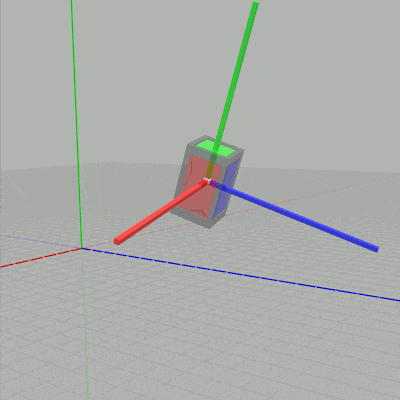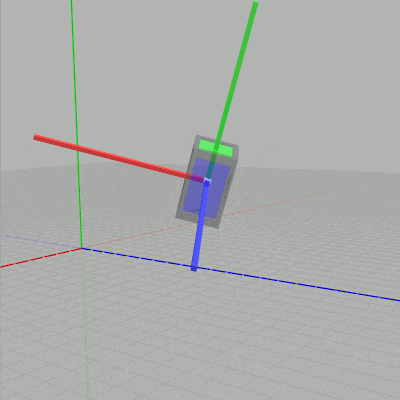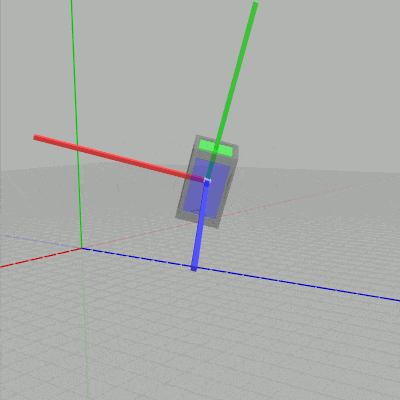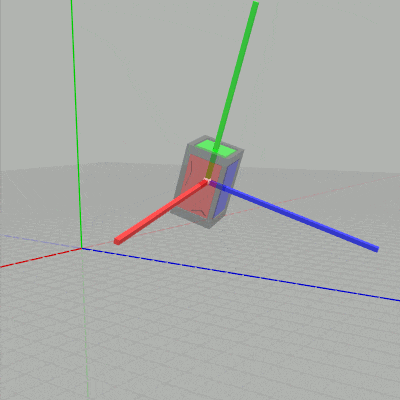
図9 ローカル座標系の y軸周りの回転 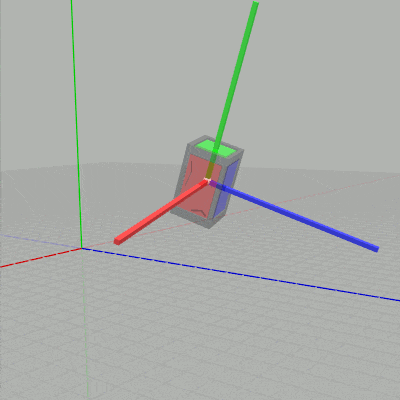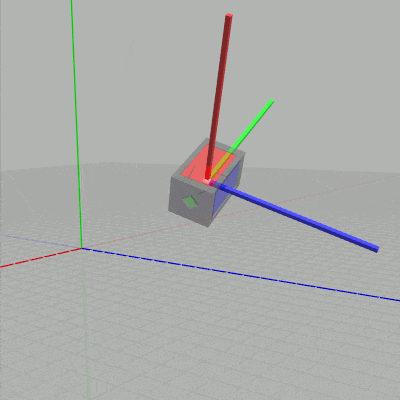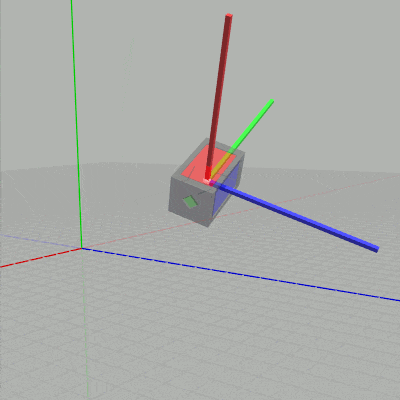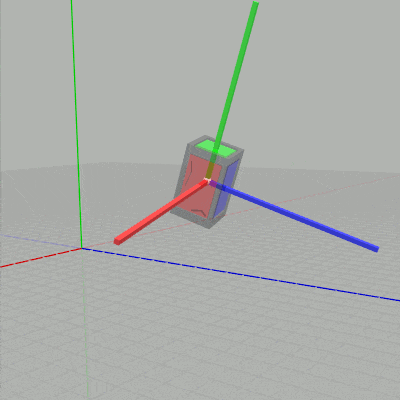
図10 ローカル座標系の z軸周りの回転
最後に本節で述べた内容に関してのプログラムを作成する。
しかし、コンピューターグラフィックスで使われる変換行列についてはその面倒な計算を回避できることが多い。なぜならコンピューターグラフィックスで使われる変換行列はスケール行列、回転行列、平行移動行列だけで構成されることが多く、そのような場合には4-5節で述べたTRS分解が可能となるためである (ただしスケールに関してはそこで述べた制限に従っている必要がある)。
以下、$4\times4$ 行列 $M$ をTRS分解可能な変換行列であるとする。
このとき、$M$ は適当な平行移動行列 $T$、回転行列 $R$、スケール行列 $S$ によって\[ M = TRS \]のように分解することができる。
$M$ の逆行列 $M^{-1}$ は\[ M^{-1} = (TRS)^{-1} = S^{-1}R^{-1}T^{-1} \]であるから、$M^{-1}$ を求めるには3つの逆行列 $S^{-1}$、$R^{-1}$、$T^{-1}$ の積を計算すればよい。
しかし $S^{-1}$、$T^{-1}$ はスケール行列、平行移動行列であるから\[S^{-1} = \begin{pmatrix}{s_x}' &0 &0 &0 \\0 &{s_y}' &0 &0 \\ 0 &0 &{s_z}' &0 \\0 &0 &0 &1\end{pmatrix} \qquad T^{-1} = \begin{pmatrix}1 &0 &0 &{t_x}' \\0 &1 &0 &{t_y}' \\ 0 &0 &1 &{t_z}' \\0 &0 &0 &1\end{pmatrix} \]の形で表されるが、この場合のスケール成分 $({s_x}',\ {s_y}',\ {s_z}')$、平行移動成分 $({t_x}',\ {t_y}',\ {t_z}')$ を求めることは難しくはない。また、回転行列 $R$ の逆行列 $R^{-1}$ は3-11節で述べたように $R$ の転置行列 $R^{T}$ に等しい ($R^{-1} = R^{T}$ ; 回転行列が同次座標に対応する $4\times4$ 行列の形でもこれは成り立つ)。
したがって、$M^{-1}$ を求める際にはプログラム中で3つの逆行列 $S^{-1}$、$R^{-1}$、$T^{-1}$ の積を計算するよりも、スケール成分 $({s_x}',\ {s_y}',\ {s_z}')$、平行移動成分 $({t_x}',\ {t_y}',\ {t_z}')$ をまず求め、$R^{-1}$ をもとにして直接 $M^{-1}$ を作る方が効率的である。
以上をふまえて変換行列 $M$ の逆行列を求めるプログラムを作成するが、これは読者用の課題である。
今回のプログラムでは S キーが押される度に3行目において M に適当な $4\times4$ 行列がセットされるが、この行列はTRS分解可能な変換行列である。ここでの課題はこの M の逆行列を求めることである。ただし逆行列を求める際にはプログラム中で行列の積を使わずに求めるものとする。
[Code1] (実行結果 図11)
図11 Code1 実行結果 5行目の Inv は逆行列をセットするための変数である。7行目の Check(..) は Inv にセットされた逆行列が正しいかどうかを調べるための補助的なメソッドであり、具体的には Inv の各列と M.inverse の各列が完全に一致しているかどうかを比較するものである (inverse はUnityにあらかじめ用意されている逆行列を表すプロパティ)。
2つの行列の各列が完全に一致していれば、このメソッドはコンソールに
「c1 : 0.0 , c2 : 0.0, c3 : 0.0 , c4 : 0.0」
の形の出力をする (右図)。これは2つの行列の各列の差(各列の差の大きさ)がすべて $0$ であることを意味している (2つの行列の各列を $\boldsymbol{c_i}$、$\boldsymbol{d_i}$ とするとき($1\leq i \leq 4)$、すべての列で $|\boldsymbol{c_i} - \boldsymbol{d_i}| = 0$)。
最初の段階では identity がセットされているので、各列の差はいずれも $0$ にはならない。
なお Matrix4x4 をコンストラクタ経由で作成するには、以下のように第1引数~第4引数に行列の1列目~4列目をセットすればよい。
(解答例については Sec407_Ans.txt 参照。ファイルはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)
Matrix4x4 worldObj3 = localObj1 * localObj2 * localObj3; Matrix4x4 worldObj2 = localObj1 * localObj2; Matrix4x4 worldObj1 = localObj1; Obj3.SetMatrix(worldObj3); Obj2.SetMatrix(worldObj2); Obj1.SetMatrix(worldObj1);
Matrix4x4 worldObj1 = localObj1; Matrix4x4 worldObj2 = worldObj1 * localObj2; Matrix4x4 worldObj3 = worldObj2 * localObj3;
一方で単一のオブジェクトに実行する変換行列の計算は、一部の例外を除き今までのプログラムでは以下のように行われていた。
Matrix4x4 S = GetScale4x4(sx, sy, sz); Matrix4x4 R = GetRotation4x4(degree, axis); Matrix4x4 T = GetTranslation4x4(tx, ty, tz); Matrix4x4 M = T * R * S; Obj.SetMatrix(M);
しかし最終的にオブジェクトに対して実行する5行目の変換行列 $M$ は、実際のプログラムにおいて行列の積として求める必要はない。$M$ はスケール行列 $S$、回転行列 $R$、平行移動行列 $T$ をこの順番で掛けたものである。4-5節で述べたように $T$、$R$、$S$ を
\[T = \begin{pmatrix}1 &0 &0 &t_x \\0 &1 &0 &t_y \\ 0 &0 &1 &t_z \\0 &0 &0 &1\end{pmatrix} \qquad R = \begin{pmatrix}r_{00} &r_{01} &r_{02} &0 \\r_{10} &r_{11} &r_{12} &0 \\r_{20} &r_{21} &r_{22} &0 \\0 &0 &0 &1 \end{pmatrix} \qquad S = \begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\ 0 &0 &s_z &0 \\0 &0 &0 &1\end{pmatrix}\]
とするとき、$M = TRS$ を計算すると\begin{align*}M = TRS &= \begin{pmatrix}1 &0 &0 &t_x \\0 &1 &0 &t_y \\ 0 &0 &1 &t_z \\0 &0 &0 &1\end{pmatrix}\begin{pmatrix}r_{00} &r_{01} &r_{02} &0 \\r_{10} &r_{11} &r_{12} &0 \\r_{20} &r_{21} &r_{22} &0 \\0 &0 &0 &1 \end{pmatrix} \begin{pmatrix}s_x &0 &0 &0 \\0 &s_y &0 &0 \\ 0 &0 &s_z &0 \\0 &0 &0 &1\end{pmatrix} \\\\&=\begin{pmatrix}s_x r_{00} &s_y r_{01} &s_z r_{02} &t_x \\s_x r_{10} &s_y r_{11} &s_z r_{12} &t_y \\s_x r_{20} &s_y r_{21} &s_z r_{22} &t_z \\0 &0 &0 &1 \end{pmatrix} \\\\\end{align*}
となる。この計算結果からわかるように、$M$ の1列目は $R$ の1列目に $s_x$ を掛けたもの、$M$ の2列目は $R$ の2列目に $s_y$ を掛けたもの、$M$ の3列目は $R$ の3列目に $s_z$ を掛けたものであり、$M$ の4列目は $T$ の4列目と同じである。
したがって単一のオブジェクトの場合、その変換行列は $M = TRS$ のように3つの行列の積を計算するのではなく、回転行列 $R$ をもとにして次のように直接'作る'ことができるのである。もちろん3つの行列の積を計算するよりは明らかに効率的である (以下の r[i, j] は解説中の $r_{ij}$ と同じである)。
Matrix4x4 r = GetRotation4x4(degree, Vector3.forward); Vector4 c1 = new Vector4(sx * r[0, 0], sx * r[1, 0], sx * r[2, 0], 0.0f); // 1列目 Vector4 c2 = new Vector4(sy * r[0, 1], sy * r[1, 1], sy * r[2, 1], 0.0f); // 2列目 Vector4 c3 = new Vector4(sz * r[0, 2], sz * r[1, 2], sz * r[2, 2], 0.0f); // 3列目 Vector4 c4 = new Vector4(tx, ty, tz, 1.0f); // 4列目 Matrix4x4 M = new Matrix4x4(c1, c2, c3, c4); Obj.SetMatrix(M);
では単一のオブジェクトの行列計算に使われるスケール成分 $(s_x, s_y, s_z)$、回転成分 $(r_{00}, r_{10}, r_{20})$、$(r_{01}, r_{11}, r_{21})$、$(r_{02}, r_{12}, r_{22})$、平行移動成分 $(t_x, t_y, t_z)$ を個別に変化させるとオブジェクトはどのように変化するのであろうか。
以下簡単な例を通して実際に見ていこう。


図1はオブジェクト Cube の初期状態である。Cubeは初期状態では立方体であり、その中心が原点に置かれている。図2はCubeに対し適当なスケール、回転、平行移動をこの順で行ったときのものであるが、このときのスケール成分を $(s_x, s_y, s_z)$、平行移動成分 $(t_x, t_y, t_z)$ で表し、Cubeに実行されている回転行列を小文字の $\large\boldsymbol{\mathsf{r}}$ で表す。
便宜上、プログラムにおける変換行列の計算には CalcMatrix(..) という以下のメソッドを使用する (上のコードをメソッド化したものである)。
Matrix4x4 CalcMatrix(Vector3 s, Matrix4x4 r, Vector3 t)
{
Vector4 c1 = new Vector4(s.x * r[0, 0], s.x * r[1, 0], s.x * r[2, 0], 0.0f);
Vector4 c2 = new Vector4(s.y * r[0, 1], s.y * r[1, 1], s.y * r[2, 1], 0.0f);
Vector4 c3 = new Vector4(s.z * r[0, 2], s.z * r[1, 2], s.z * r[2, 2], 0.0f);
Vector4 c4 = new Vector4(t.x, t.y, t.z, 1.0f);
return new Matrix4x4(c1, c2, c3, c4);
}
まず図2の状態から平行移動成分 $(t_x, t_y, t_z)$ だけを変化させる場合である (X、Y、Z の各キーを押すことで $t_x$、$t_y$、$t_z$ が個別に変化する)。
float mv = THUtil.IsShiftDown() ? -1 : 1;
if (Input.GetKeyDown(KeyCode.X)) { t.x += mv; }
else if (Input.GetKeyDown(KeyCode.Y)) { t.y += mv; }
else if (Input.GetKeyDown(KeyCode.Z)) { t.z += mv; }
else { return; }
Matrix4x4 M = CalcMatrix(s, r, t);
Cube.SetMatrix(M);
下図に示されるように $t_x$ を変化させるとCubeのオブジェクト原点が、オブジェクト原点を通る x軸に平行な直線上を移動することになる。$t_y$ を変化させるとオブジェクト原点を通る y軸に平行な直線上を移動することになる。


続いては図2の状態からスケール成分 $(s_x, s_y, s_z)$ だけを変化させる場合である (X、Y、Z の各キーを押すことで $s_x$、$s_y$、$s_z$ が個別に変化する)。
float ad = THUtil.IsShiftDown() ? -0.2f : 0.2f;
if (Input.GetKeyDown(KeyCode.X)) { s.x += ad; }
else if (Input.GetKeyDown(KeyCode.Y)) { s.y += ad; }
else if (Input.GetKeyDown(KeyCode.Z)) { s.z += ad; }
else { return; }
Matrix4x4 M = CalcMatrix(s, r, t);
Cube.SetMatrix(M);
$s_y$ だけを変化させると下左図に示されるように、Cubeがローカル座標系の y軸に沿って拡大縮小する (ローカル座標系については次節で解説する)。$s_z$ だけを変化させると下右図に示されるように、Cubeがローカル座標系の z軸に沿って拡大縮小する。


続いては図2の状態のCubeに対し x軸周り、y軸周り、z軸周りの回転行列を個別に実行する。下のコードにおいて r は現在の回転状態を表す回転行列であり、Rx、Ry、Rz は x軸、y軸、z軸周りの回転を表す回転行列である (回転角度は $\pm 10^\circ$ )。
float deg = THUtil.IsShiftDown() ? -10 : 10;
Matrix4x4 Rx = TH3DMath.GetRotation4x4(deg, Vector3.right);
Matrix4x4 Ry = TH3DMath.GetRotation4x4(deg, Vector3.up);
Matrix4x4 Rz = TH3DMath.GetRotation4x4(deg, Vector3.forward);
if (Input.GetKeyDown(KeyCode.X)) { r = Rx * r; }
else if (Input.GetKeyDown(KeyCode.Y)) { r = Ry * r; }
else if (Input.GetKeyDown(KeyCode.Z)) { r = Rz * r; }
else { return; }
Matrix4x4 M = CalcMatrix(s, r, t);
Cube.SetMatrix(M);
X キーが押されると図2の状態から下左図の赤い点線を回転軸として、$10^\circ$ あるいは $-10^\circ$ ずつ回転する (赤い点線はオブジェクト原点を通る x軸に平行な直線)。Y キーが押されると図2の状態から下右図の緑の点線を回転軸として、$10^\circ$ あるいは $-10^\circ$ ずつ回転する (緑の点線はオブジェクト原点を通る y軸に平行な直線)。


つまり変換行列の回転成分に対し x軸周り、y軸周り、z軸周りの回転行列を掛けるとオブジェクトは、自身のオブジェクト原点を通り x軸、y軸、z軸に平行な軸の周りに回転するのである。
列優先の場合には新しい行列を左に掛けていくので、現在の状態からさらに回転させるために上のコードでは回転行列 Rx、Ry、Rz を左に掛けたわけである。もしこれらの回転行列を左ではなく右に掛けると、すなわち上記コードの6~8行目を次のように変更すると
if (Input.GetKeyDown(KeyCode.X)) { r = r * Rx; }
else if (Input.GetKeyDown(KeyCode.Y)) { r = r * Ry; }
else if (Input.GetKeyDown(KeyCode.Z)) { r = r * Rz; }


最後に本節で述べた内容に関してのプログラムを作成する。
# Code1
行列計算においては逆行列を必要とする場合がしばしば生じるが、残念ながら逆行列はそれを求める際の計算量が多く、特に $4\times4$ 行列などはまともにやるとその計算量が非常に高くつく。しかし、コンピューターグラフィックスで使われる変換行列についてはその面倒な計算を回避できることが多い。なぜならコンピューターグラフィックスで使われる変換行列はスケール行列、回転行列、平行移動行列だけで構成されることが多く、そのような場合には4-5節で述べたTRS分解が可能となるためである (ただしスケールに関してはそこで述べた制限に従っている必要がある)。
以下、$4\times4$ 行列 $M$ をTRS分解可能な変換行列であるとする。
このとき、$M$ は適当な平行移動行列 $T$、回転行列 $R$、スケール行列 $S$ によって\[ M = TRS \]のように分解することができる。
$M$ の逆行列 $M^{-1}$ は\[ M^{-1} = (TRS)^{-1} = S^{-1}R^{-1}T^{-1} \]であるから、$M^{-1}$ を求めるには3つの逆行列 $S^{-1}$、$R^{-1}$、$T^{-1}$ の積を計算すればよい。
しかし $S^{-1}$、$T^{-1}$ はスケール行列、平行移動行列であるから\[S^{-1} = \begin{pmatrix}{s_x}' &0 &0 &0 \\0 &{s_y}' &0 &0 \\ 0 &0 &{s_z}' &0 \\0 &0 &0 &1\end{pmatrix} \qquad T^{-1} = \begin{pmatrix}1 &0 &0 &{t_x}' \\0 &1 &0 &{t_y}' \\ 0 &0 &1 &{t_z}' \\0 &0 &0 &1\end{pmatrix} \]の形で表されるが、この場合のスケール成分 $({s_x}',\ {s_y}',\ {s_z}')$、平行移動成分 $({t_x}',\ {t_y}',\ {t_z}')$ を求めることは難しくはない。また、回転行列 $R$ の逆行列 $R^{-1}$ は3-11節で述べたように $R$ の転置行列 $R^{T}$ に等しい ($R^{-1} = R^{T}$ ; 回転行列が同次座標に対応する $4\times4$ 行列の形でもこれは成り立つ)。
したがって、$M^{-1}$ を求める際にはプログラム中で3つの逆行列 $S^{-1}$、$R^{-1}$、$T^{-1}$ の積を計算するよりも、スケール成分 $({s_x}',\ {s_y}',\ {s_z}')$、平行移動成分 $({t_x}',\ {t_y}',\ {t_z}')$ をまず求め、$R^{-1}$ をもとにして直接 $M^{-1}$ を作る方が効率的である。
以上をふまえて変換行列 $M$ の逆行列を求めるプログラムを作成するが、これは読者用の課題である。
今回のプログラムでは S キーが押される度に3行目において M に適当な $4\times4$ 行列がセットされるが、この行列はTRS分解可能な変換行列である。ここでの課題はこの M の逆行列を求めることである。ただし逆行列を求める際にはプログラム中で行列の積を使わずに求めるものとする。
[Code1] (実行結果 図11)
if (Input.GetKeyDown(KeyCode.S))
{
Matrix4x4 M = GetTRSMatrix();
Matrix4x4 Inv = Matrix4x4.identity;
Check(Inv, M.inverse);
}

2つの行列の各列が完全に一致していれば、このメソッドはコンソールに
「c1 : 0.0 , c2 : 0.0, c3 : 0.0 , c4 : 0.0」
の形の出力をする (右図)。これは2つの行列の各列の差(各列の差の大きさ)がすべて $0$ であることを意味している (2つの行列の各列を $\boldsymbol{c_i}$、$\boldsymbol{d_i}$ とするとき($1\leq i \leq 4)$、すべての列で $|\boldsymbol{c_i} - \boldsymbol{d_i}| = 0$)。
最初の段階では identity がセットされているので、各列の差はいずれも $0$ にはならない。
なお Matrix4x4 をコンストラクタ経由で作成するには、以下のように第1引数~第4引数に行列の1列目~4列目をセットすればよい。
// c1, c2, c3, c4 は行列の1列目から4列目 (Vector4型) Matrix4x4 Inv = new Matrix4x4(c1, c2, c3, c4);
(解答例については Sec407_Ans.txt 参照。ファイルはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)
© 2020-2025 Redpoll's 60 (All rights reserved)