Redpoll's 60
Home / 3Dプログラミング入門 / 第4章 $§$4-13
第4章 3D空間におけるオブジェクトの運動
$§$4-13 ローカル座標とワールド座標の相互変換
前節では親子関係にあるオブジェクトの各階層において、オブジェクト上のある位置を計算すること、すなわち オブジェクトのローカル座標を指定の座標系での値に変換することについて見てきた。それは1階層上の座標系であったり2階層上での座標系、あるいはワールド座標系であったが、その内容は座標変換の算出過程なども順を追って解説するなど、いささか教科書的なものであった。
しかし 実際のプログラム実行中における座標変換とは、ローカル座標をワールド座標に変換する、あるいはその逆にワールド座標をローカル座標に変換するといったケースがほとんどである。本節ではそういった実用的なケースについていくつかの例を通して見ていく。
図2はGreenに対して適当な変換を実行したときのものである。

図1 Green 初期状態 (青い頂点が V1、赤い頂点が V2) 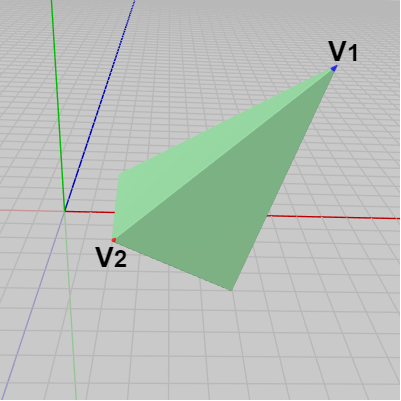
図2 Greenに対して適当な変換を実行
次のプログラムは変換後のGreenの青い頂点 $V_1$、赤い頂点 $V_2$ の座標を計算し、この2つの頂点に図3に示される小さな球を配置するものである (青い球を青い頂点へ、赤い球を赤い頂点へ置く。2つの球は初期状態でその中心が原点に置かれている)。
図3 BallB 初期状態 (青い球と赤い球があり2つの球は同じ大きさ) 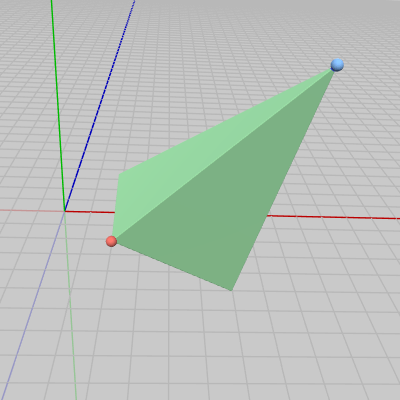
図4 Code1 実行結果
[Code1] (実行結果 図4)
8行目まではGreenに対する変換の実行であり、この変換によってGreenは図2の状態になる。
Greenに実行される行列は M であるが、Greenは親子関係のない単独のオブジェクトであるのでこの M はGreenのワールド行列である。
変換後のGreenの2つの頂点 $V_1$、$V_2$ の(ワールド)座標を求めるには、Greenに実行されているワールド行列と初期状態における $V_1$、$V_2$ の同次座標との積を計算すればよい。
プログラム10~11行目がその計算である。c_initV1、c_initV2 は初期状態における $V_1$、$V_2$ の座標を表すVector3型定数であり、V1、V2 は変換後の $V_1$、$V_2$ の座標である (ToVector4(..) は3次元ベクトルを $(x, y, z, 1)$ の形の同次座標にするカスタムライブラリーのメソッド)。
12~13行目の BallB、BallR は上記の小さな青い球、赤い球を表すオブジェクトである。この2つの球を V1、V2 に移動させると実行結果(図4)に示されるように変換後のGreenの2つの頂点に置かれることになる。
なお 12~13行目の SetWorldPosition(Vector3 v) はオブジェクトを引数で指定された分だけ平行移動させるカスタムライブラリーのメソッドであり、次の記述と同等である。
図中の $V_0$~$V_7$ はBoxの各頂点を表している。初期状態においてBoxの各辺は x軸、y軸、z軸に平行なので、例えば頂点 $V_0$ の座標は $(0.5,\ 0.5, -0.5)$ であり、頂点 $V_5$ の座標は $(0.5, -0.5,\ 0.5)$ である。
図6はBoxに対して適当な回転及びスケールが行われている様子である。
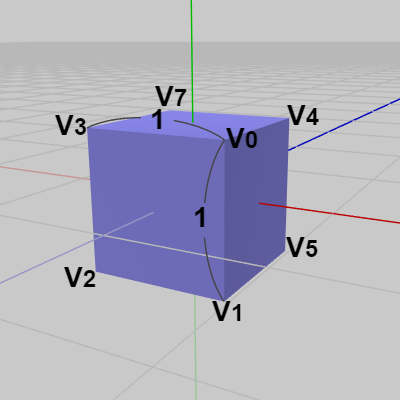
図5 Box 初期状態 
図6 Boxの運動
今回のプログラムでは上図に示される運動を行っているBoxの各頂点に、図7の小さな白い球が常に置かれるようにする (この白い球は8個あり、初期状態ではその中心が原点に置かれている)。
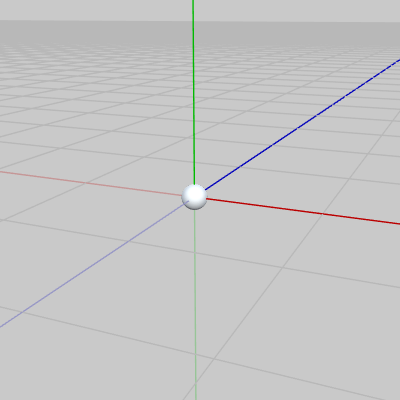
図7 MiniBall 初期状態 
図8 Code2 実行結果
プログラムは以下のとおり。
[Code2] (実行結果 図8)
1行目の BoxMotion() はBoxを上図に示されるような運動を行わせるためのもので、毎フレーム 指定の位置における回転及びスケールがBoxに対して実行される。3行目の M はその時点で実行されているBoxの変換行列、すなわち その時点におけるBoxのワールド行列である。
プログラム中の MiniBall は上図6の小さい白い球を表すオブジェクトであり、要素数 8 の配列である。7行目はその時点におけるBoxの各頂点座標の計算であり、ここで使われている c_initBoxVerts は初期状態のBoxの各頂点 $V_0$~$V_7$ の座標である (上図5における $V_0$~$V_7$ の座標)。
計算内容はCode1と同様であり、現時点におけるBoxのワールド行列と初期状態における各頂点の同次座標との積を計算し、現時点での各頂点のワールド座標を求めるというものである。実行結果(図8)に示されるように、毎フレーム 変化するBoxの各頂点に白い球が常に置かれることになる。
図9はオブジェクト Base の初期状態であり、初期状態ではBaseの底面の中心は原点に置かれている。図10はオブジェクト Beam の初期状態である。Beamは細長い直方体であり、初期状態においてはその底面の中心が原点に置かれている。図11は先程使われた四角錐型のオブジェクト Green の初期状態である。ここでもGreenの青い頂点を $V_1$、赤い頂点を $V_2$ とする。
図12は各オブジェクトの階層構造であるが、Baseが一番上の親オブジェクト、Greenが一番下の子オブジェクトである。
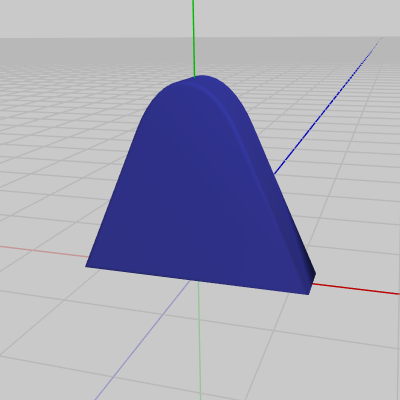
図9 Base 初期状態 
図10 Beam 初期状態

図11 Green 初期状態 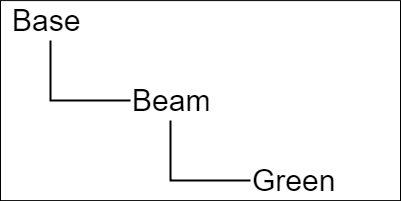
図12 オブジェクトの階層構造
今 この3つのオブジェクトが下図13に示されるような運動を行っているとする (Baseは指定の位置において適当な回転が行われた状態で静止しており、BeamはBaseの上で一定の範囲を往復回転している。また GreenはそのBeamの上面の一方の端で拡大縮小を繰り返している)。

図13 3つのオブジェクトの一体化した運動 
図14 Code3 実行結果
今回は上記のように一体化した運動を行っているGreenの2つの頂点 $V_1$、$V_2$ に、Code1でも用いた青い球と赤い球が常に置かれるようにする。
プログラムは以下のとおり。
[Code3] (実行結果 図14)
12行目までは3つのオブジェクトの一体化運動に関する記述である。3つのオブジェクトの運動自体は別の箇所に記述されており、毎フレーム CalcLocalMatrices() (1行目)によって各オブジェクトのローカル行列を取得する (返される値は Green、Beam、Base のローカル行列がセットされた配列である)。
14行目以降はCode1と同じ内容である。現時点での $V_1$ と $V_2$ のワールド座標を算出し、青い球を $V_1$ に、赤い球を $V_2$ に移動させる。これを毎フレーム行うことで実行結果(図14)に示されるように2つの球が2つの頂点に常に置かれるようになる。
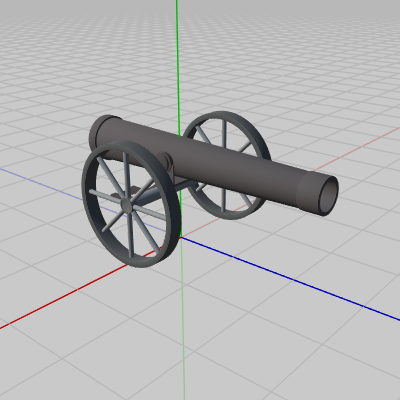
図15 Cannon 初期状態 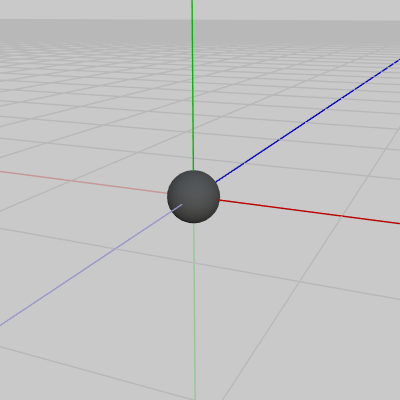
図16 Shell 初期状態
Cannonは初期状態において z軸プラス方向を向いている。下図17における点 $S$ はCannonの初期状態におけるShellの発射開始位置であり、$\boldsymbol{\mathsf{v}}$ は発射方向を表す単位ベクトルである (初期状態においては発射方向 $\boldsymbol{\mathsf{v}}$ は z軸プラス方向)。

図17 初期状態における発射開始位置 S と発射方向 v 
図18 Cannonに適当な変換を行った状態
図18はCannonに適当な変換(平行移動 + 回転)を行ったときのものであるが、このときの Shell発射開始位置、及び発射方向は次のように求められる。
Code1~Code3ではGreenやBoxに適当な変換を行い、GreenやBoxの変換後の頂点座標を計算したがここでも考え方は同じである。Cannonの変換後における発射開始位置は、変換後のCannonのワールド行列と初期状態における発射開始位置 $S$ の同次座標との積を計算すればよい。
具体的には以下のように記述される。
mtx はCannonのワールド行列、c_initShootPosition は初期状態における発射開始位置 $S$ のことであり、shootPos が変換後の発射開始位置である。
前節の終わりで述べたように、オブジェクトに対して何らかの変換が行われ、その変換後のオブジェクトの向き(ワールド座標系における向き)を計算するには、その時点でのオブジェクトのワールド行列と初期状態におけるオブジェクトの向きを表すベクトルとの積を計算すればよい。ただし その際にはベクトルを($w = 1$ ではなく) $w = 0$ で同次座標化する必要がある。
今回の例では図18の状態におけるShellの発射方向の計算であるが、この場合には図18の時点でのCannonのワールド行列と初期状態における発射方向 $\boldsymbol{\mathsf{v}}$ との積を計算する。そしてその計算の際には $\boldsymbol{\mathsf{v}}$ を $w=0$ で同次座標化したものを使う。
具体的には以下のとおり。
2行目の c_initShootDirection は初期状態における発射方向 $\boldsymbol{\mathsf{v}}$ を表すVector3型の定数であり、図17に示されるようにその値は z軸プラス方向 $(0, 0, 1)$ である。v4 は $\boldsymbol{\mathsf{v}}$ を $w=0$ で同次座標化した4次元ベクトルである (UnityではVector4にVector3を代入すると自動的に w座標が $0$ になる)。3行目の shootDir が変換後のCannonの発射方向である。
なお 上の記述は次のように簡略化できる。
2行目の mtx * c_initShootPosition は Matrix4x4 と Vector3 の積の計算である。数学的には $4\times4$行列と3次元ベクトルの積は定義されないが、Unityではこの場合 Vector3 が自動的に Vector4 に変換されて計算される。そしてその際 Vector4 の w座標に $0$ がセットされるのである。
なお本節で使用するShellはカスタムライブラリーの THShell3D 型のインスタンスであるが、THShell3D クラスにはShellの動作に関連するいくつかのプロパティが用意されている。

図19 Code4 実行結果
次のプログラムは上図18の状態のCannonからShellを発射するものである (Aキーを押すことでShellが発射される)。
[Code4] (実行結果 図19)
1行目のifブロックには A キーが押されるたびに入るが、ここではShellの発射開始位置、及び発射方向を計算し、Shellを開始位置に移動させることまでが行われる。3~5行目は上で述べたShellの発射開始位置、及び発射方向の計算である。
7~8行目はShellのプロパティ direction、speed へのセットである。これらのプロパティの値はShellの運動中に変化することはない。
16行目以降はShellを指定の方向に毎フレーム 指定の距離だけ移動させる処理である。具体的には毎フレーム Shellの現在地(Shell.position)から Shell.direction の方向に Shell.speed だけ進んで行く。
16~18行目は毎フレーム 実行されるので A キーが押されない限り常にShellは指定の方向に進み続ける (A キーが押されるとShellは再び発射開始位置からのスタートになる)。
球体と違って、このShellには向きがありShellを発射する際にはその発射方向に向いている必要がある。初期状態ではその向きは z軸プラス方向であるので図21に示されるように、Shellの向きを変えずに初期状態のCannonの発射開始位置 $S$ まで移動させると、そのまま発射できる状態になる (この場合にはShellの向きと発射方向 $\boldsymbol{\mathsf{v}}$ が一致している)。
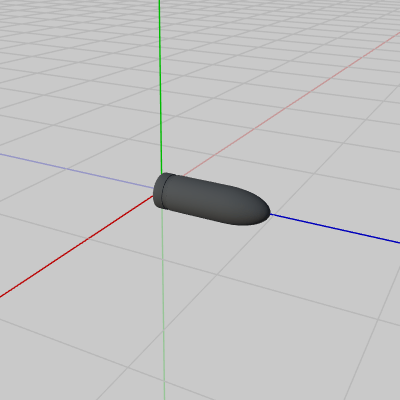
図20 Shell 初期状態 
図21 初期状態の向きはCannonと同じく +z
しかし、Cannonに何らかの回転が行われている場合には事情は異なる。
例えば下図22はCannonに対して適当な変換を行い、Shellの向きを変えずに発射開始位置に移動させたものである。図に示されるように本来はShellは発射方向である $\boldsymbol{\mathsf{v}}$ を向いていなければいけないが、向きを変えていないため z軸プラス方向を向いたままになっている。
そしてこのまま発射すると(Code4をそのまま使うと)、図23のような結果、すなわち Shellが初期状態の向きと同じ z軸プラス方向を向いた状態で進んで行くことになる。
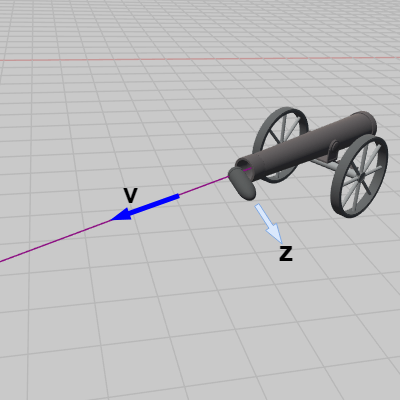
図22 本来は発射方向 v の方向を向いていなければいけないが、初期状態の方向 z軸プラス方向を向いている 
図23 z軸プラス方向を向いたまま進んで行く
Shellの発射方向とはCannonの向いている方向のことである。ある時点でCannonが $\boldsymbol{\mathsf{v_1}}$ の方向を向いていれば、発射方向も $\boldsymbol{\mathsf{v_1}}$ であり、Shellを発射する際にはShellも $\boldsymbol{\mathsf{v_1}}$ に向ける必要がある (図24)。同様に、Cannonが $\boldsymbol{\mathsf{v_2}}$ の方向を向いていれば、発射方向も $\boldsymbol{\mathsf{v_2}}$ であり、Shell発射の際にはShellも $\boldsymbol{\mathsf{v_2}}$ に向ける必要がある (図25)。

図24 
図25
Cannonに対してある回転 $R$ を行ったときにCannonの向きが $\boldsymbol{\mathsf{v}}$ になったとする。このとき発射方向は $\boldsymbol{\mathsf{v}}$ であるからShellを発射する際にはShellも $\boldsymbol{\mathsf{v}}$ の方向に向ける必要がある。問題はどのようにしてShellを $\boldsymbol{\mathsf{v}}$ の方向に向けるかということであるが、これは簡単に解決する。
Cannonは初期状態で z軸プラス方向を向いているので、Cannonに回転 $R$ を行ったときにCannonが $\boldsymbol{\mathsf{v}}$ を向いたということは、z軸プラス方向に回転 $R$ を実行すると $\boldsymbol{\mathsf{v}}$ の方向を向くことを意味する。ShellもCannonと同じく初期状態では z軸プラス方向を向いているので、Shellに対して回転 $R$ を行えばShellの向きは $\boldsymbol{\mathsf{v}}$ の方向に向けられるわけである。
つまり、ある時点においてShellの向きをCannonの向きと同じにするためには、そのときCannonに実行されている回転をShellに対しても実行すればよいのである。
次のプログラムはキー操作によってCannonの向きを変え、図20のShellをCannonから発射するものである。
キー操作は以下のとおり。
H、J、K、L : Cannonの向きを変える。
A : Shellの発射。
[Code5] (実行結果 図26)
1行目のifブロックはキー操作によってCannonの向きを変える処理である。
A キーが押されるたびに7行目のifブロックに入る。このifブロックではShellを発射開始位置に移動させるが、今回は移動させるだけでなく向きを発射方向に向けた状態にしている。具体的には16行目以降の部分である。
ローカル変数 mtx はその時点においてCannonに実行されている変換行列(ワールド行列)であり、Cannonには回転と平行移動しか行っていないので mtx は回転行列と平行移動行列の積である。
4-6節で述べたように変換行列の1~3列目はスケール成分と回転成分を表し、4列目は平行移動成分を表している。そして今回はCannonにはスケールを行っていないのでCannonに実行されている変換行列 mtx の1~3列目は回転成分のみであり、Cannonに実行されている回転だけを取り出すには mtx の4列目を $(0, 0, 0, 1)$ にすればよい (変換行列の第4列目が $(0, 0, 0, 1)$ であることは何も平行移動を行っていないことを意味する)。
16行目の SetColumn(..) は mtx の4列目を $(0, 0, 0, 1)$ にするための処理であり、これによって mtx はCannonに実行された回転を表す回転行列になる。17行目ではこの回転行列をShellのプロパティ rotMatrix にセットしている。Shellを発射する際にはまずCannonと同じ方向に向けてから発射開始位置に移動させるが、Cannonと同じ方向に向けるためにはこの rotMatrix を使えばよい。つまり、まず始めに rotMatrix によってCannonと同じ方向に向け、その次に発射開始位置に移動させれば今回の目的が達せられる (20行目)。

図26 Code5 実行結果 25行目以降は発射後のShellの移動処理であるが、Shellは移動中に向きを変えることはないのでその向きは発射時点と同じである。したがって毎フレーム rotMatrix によってShellを発射時点と同じ向きに向けてから、新しい位置に移動させている。
(上で使われた SetColumn(..) は指定の列の内容を書き換えるためのメソッドであり、最初の引数には列番号を指定するがその値は $0$ 始めである。つまり第1列目であれば引数には $0$ を、第4列目であれば $3$ をセットする必要がある。)
その例としてCannonと下図27のBatteryが親子関係を構成している場合で見ていこう。Batteryが親オブジェクトであり、Cannonが子オブジェクトである。図28はCannonをアタッチポジションに移動させたときのものであり、このときBatteryは初期状態のままである。
次のプログラムはBatteryにアタッチされているCannonからShellを発射するものである。
[Code6] (実行結果 図29)
このプログラムでは H あるいは L キーによってBatteryを回転させるが、i_degBattery はBatteryの回転角度を表すインスタンス変数である。10~20行目が一体化運動の記述であり、Batteryは指定の位置で回転を行い、Cannonはアタッチポジションまでの移動を行うだけである。
23行目以降はShell発射に関する処理であるが、この部分はCode5の7行目以降と同じである。
Cannonが親子階層に含まれていても、ワールド座標系におけるShellの発射開始位置や発射方向を求めるのであれば、それらはCannonのワールド行列から算出される。この点はCannonが単独のオブジェクトの場合のCode4やCode5と同じである。
今までのプログラムはすべてローカル座標をワールド座標に変換するものであった。以下の2つの課題はいずれもその逆であり、ワールド座標からローカル座標への変換である。
例えばレイとオブジェクトの衝突判定を行う場合などでは、レイの始点及びその進行方向をオブジェクトのローカル座標系の値に変換することが多い。オブジェクトが非常に多くの三角形の集合として構成されているような場合、毎フレーム1つ1つの三角形の各頂点のワールド座標を計算することは現実的ではない。これは2-15節でも同様のことを述べたが、そういった場合にはオブジェクトを構成するすべての三角形のワールド座標を求めるのではなく、レイの始点とその進行方向をオブジェクトのローカル座標系で測った値に変換して、オブジェクトのローカル座標系で衝突判定を行う方がはるかに効率的なのである (各三角形の頂点座標はメッシュの座標(初期状態の頂点座標)を使えばよい)。
下図はレイと直方体の衝突判定を行っているときの様子である。図中の $R_0$ はレイの始点、$\boldsymbol{\mathsf{v}}$ はレイの進行方向を表す単位ベクトルである。
直方体オブジェクト Box は初期状態において各辺が x軸、y軸、z軸に平行であり、その中心が原点に置かれている。
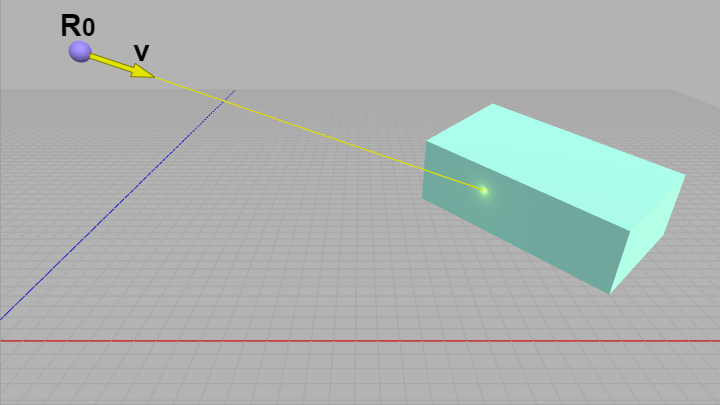
図30 レイ vs 直方体
ここで $R_0$ 及び $\boldsymbol{\mathsf{v}}$ をBoxのローカル座標系で測った値に変換することを考えよう。以下 Box座標系の x軸、y軸、z軸を $\boldsymbol{lx}$、$\boldsymbol{ly}$、$\boldsymbol{lz}$ とする (下図31)。
レイの始点 $R_0$ であれば、Box座標系の原点と $R_0$ を結ぶベクトルを $\boldsymbol{\mathsf{w}}$ とし、ワールド座標系で測った $\boldsymbol{\mathsf{w}}$ の値を $\boldsymbol{\mathsf{w}} = (a, b, c)$ とする。このとき $\boldsymbol{\mathsf{w}}$ の終点が $\boldsymbol{lx}$ 軸方向、$\boldsymbol{ly}$ 軸方向、$\boldsymbol{lz}$ 軸方向にどれだけ離れているかを求めその各値を $a'$、$b'$、$c'$ とすれば、$(a',\ b',\ c')$ が $R_0$ のBox座標系における座標となるのであった (考え方は3-4節の ijk座標系の議論と同じである)。
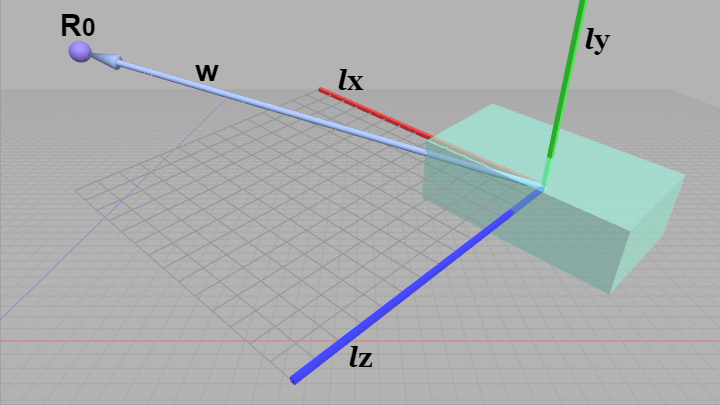
図31 $\boldsymbol{\mathsf{w}}$ はBox座標系の原点と $R_0$ を結ぶベクトル
進行方向を $\boldsymbol{\mathsf{v}}$ についても同様である。$\boldsymbol{\mathsf{v}} = (s, t, u)$ とするとき ($s$、$t$、$u$ はワールド座標系で測った値)、$\boldsymbol{\mathsf{v}}$ の始点をBox座標系の原点に移動させても $\boldsymbol{\mathsf{v}}$ の各成分は $(s, t, u)$ のまま変わらない。したがって先程の $\boldsymbol{\mathsf{w}}$ と同様に、(原点を始点とする)単位ベクトル $\boldsymbol{\mathsf{v}}$ の終点が $\boldsymbol{lx}$ 軸方向、$\boldsymbol{ly}$ 軸方向、$\boldsymbol{lz}$ 軸方向にどれだけ離れているかを求めれば、それが $\boldsymbol{\mathsf{v}}$ のBox座標系における進行方向である。
プログラムには以下の2つの定数が用意されている。
この2つの定数 R0、v はいずれもワールド座標である。
プログラムは最初の段階では以下の処理が記述されている。
[Code7] (実行結果 図32)
Boxには毎フレーム回転のみが実行されるので、プログラム実行中はBoxは同じ位置でただ回転のみを行う。1行目では毎フレーム Boxに実行されているワールド行列を取得しているが、Boxにはスケールは実行されていないのでこのワールド行列の1列目~3列目の大きさはいずれも $1$ である。
3行目、5行目の loc_R0、loc_v は、$R_0$、$\boldsymbol{\mathsf{v}}$ のBox座標系における値をセットするための変数であるが、最初の段階では適当な値がセットされている。Boxのワールド行列 M と2つの定数 R0、v をもとにして、この loc_R0、loc_v に適切な値をセットすることがここでの課題である (8行目以降の処理については変更する必要はない)。
なおこの課題においてワールド座標 R0、v をBoxのローカル座標 loc_R0、loc_v に変換する際には、Boxのワールド行列の逆行列を使ってはいけないものとする。
下図の左側の十字はレイの始点 $R_0$ の位置を示し、図中の小さな赤い球はレイの進行方向を示している (レイは $R_0$ から赤い球に向かって進んでいく)。
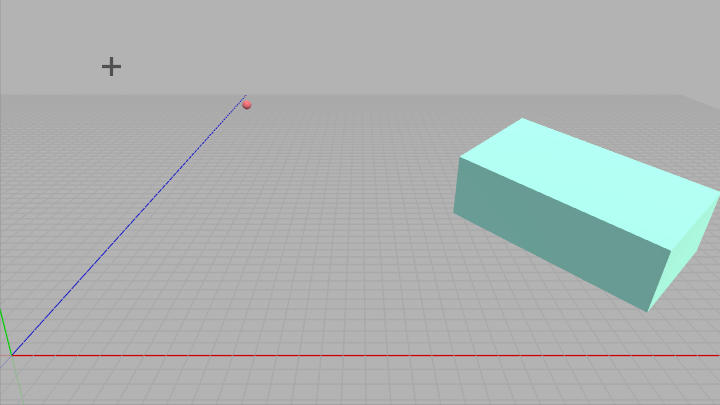
図32 左側の十字はレイの始点 $R_0$ の位置を示す。レイは $R_0$ から図中の赤い小球に向かって進んでいく。
loc_R0、loc_v へ適切な値がセットされれば、下図に示されるように十字の位置には青い球が置かれ、そこから赤い小球に向けて黄色い直線(レイ)が引かれる (実行中はレイの開始位置も進行方向も変化しない)。
しかし loc_R0、loc_v への変換が適切でなかった場合には、青い球や黄色い直線は異なる位置に表示されることになるので注意。
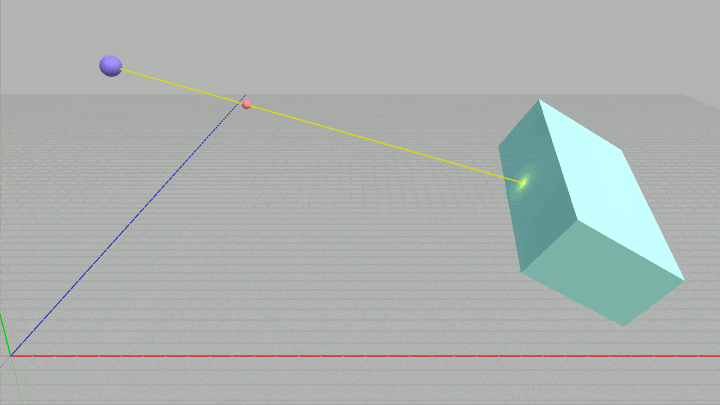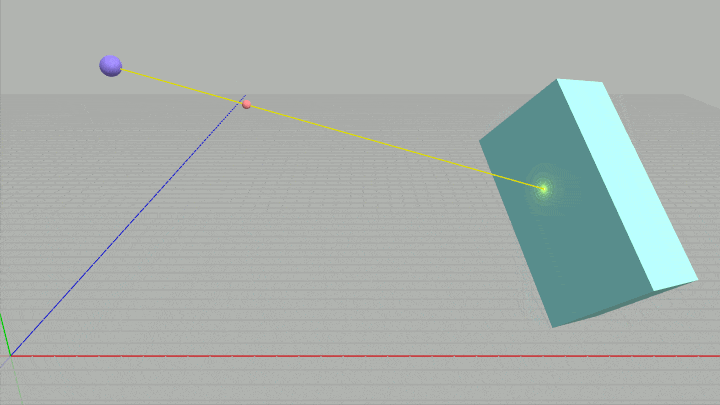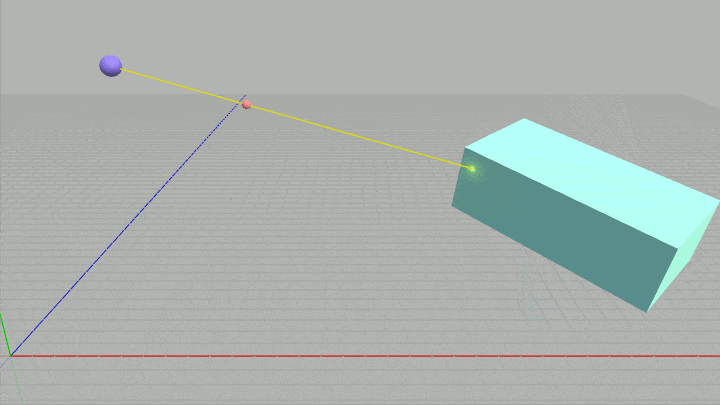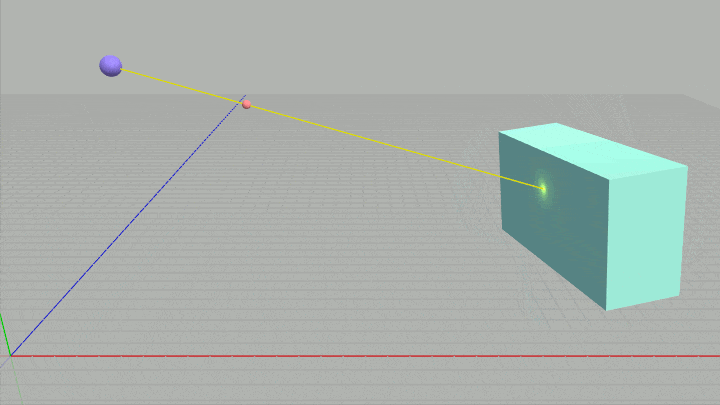
図33 Code7 実行結果
下図は今回使用する正12面体オブジェクト Blue である。今回のプログラムではBlueは同じ位置において繰り返しスケールと回転をし続ける (図35)。
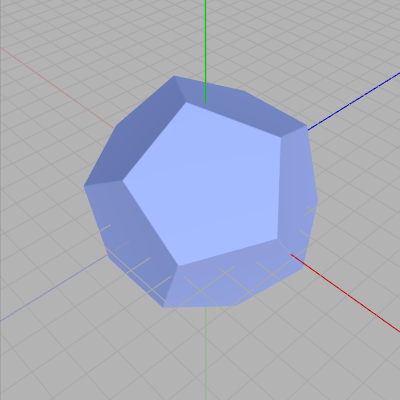
図34 Blue 初期状態 
図35 スケールと回転を繰り返す
ここでの課題もレイの始点 $R_0$ と進行方向 $\boldsymbol{\mathsf{v}}$ をBlueのローカル座標系で測った値に変換することである。そして今回はローカル座標への変換を行う際に、Blueのワールド行列の逆行列を使って変換を行うものとする。
上のプログラムでは逆行列を使わないという制限があったが、ここではその逆でありワールド座標からローカル座標への変換は、Blueに実行されているワールド行列の逆行列を使って変換を行うということである。
プログラムには先程と同じくレイの始点を表す R0、進行方向を表す v の2つのVector3型定数が用意されている (いずれもワールド座標)。
プログラムは最初の段階では以下の処理が記述されている。
[Code8] (実行結果 図36)
1行目の M がBlueに実行されているワールド行列、2行目の Inv がその逆行列である。このプログラムにおいてもワールド座標 R0、v をBlue座標系のローカル座標に変換し、それぞれ loc_R0、loc_v にセットすればよい (9行目以降の処理は変更する必要はない)。
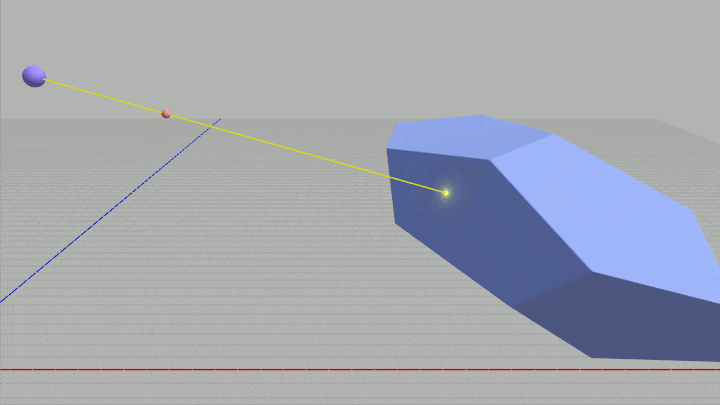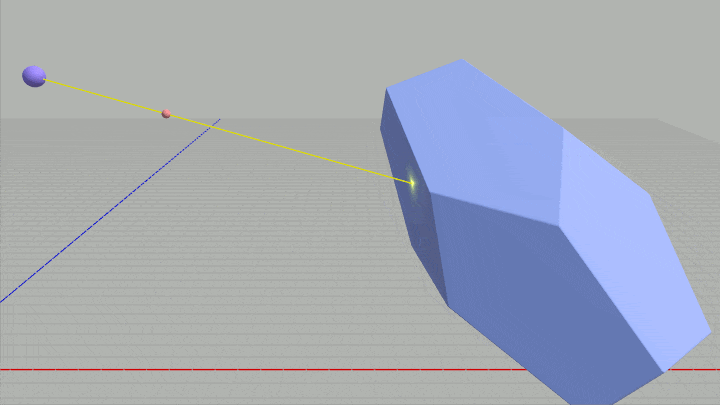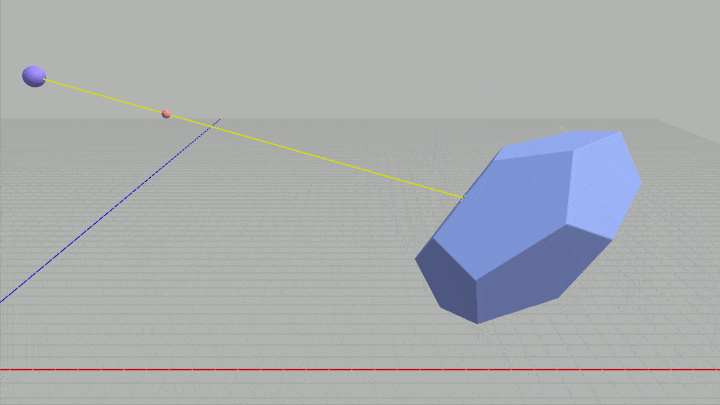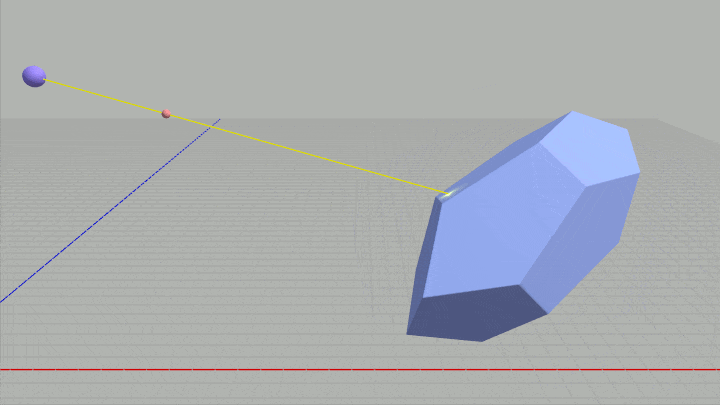
図36 Code8 実行結果
(解答例のプログラムは Sec413_Ans.txt を参照 ; Sec413_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
しかし 実際のプログラム実行中における座標変換とは、ローカル座標をワールド座標に変換する、あるいはその逆にワールド座標をローカル座標に変換するといったケースがほとんどである。本節ではそういった実用的なケースについていくつかの例を通して見ていく。
# Code1
図1はオブジェクト Green の初期状態である。Greenは四角錐であり、初期状態においてはその底面の中心が原点に位置している。初期状態におけるGreenの青い頂点を $V_1$、赤い頂点を $V_2$ とする。図2はGreenに対して適当な変換を実行したときのものである。


次のプログラムは変換後のGreenの青い頂点 $V_1$、赤い頂点 $V_2$ の座標を計算し、この2つの頂点に図3に示される小さな球を配置するものである (青い球を青い頂点へ、赤い球を赤い頂点へ置く。2つの球は初期状態でその中心が原点に置かれている)。


[Code1] (実行結果 図4)
if (!i_INITIALIZED)
{
Matrix4x4 T = TH3DMath.GetTranslation4x4(4, 5, -10);
Matrix4x4 R = TH3DMath.GetEulerRotation4x4(30, 80, -20);
Matrix4x4 S = TH3DMath.GetScale4x4(1.0f, 2.2f, 1.5f);
Matrix4x4 M = T * R * S;
Green.SetMatrix(M);
Vector3 V1 = M * TH3DMath.ToVector4(c_initV1);
Vector3 V2 = M * TH3DMath.ToVector4(c_initV2);
BallB.SetWorldPosition(V1);
BallR.SetWorldPosition(V2);
i_INITIALIZED = true;
}
8行目まではGreenに対する変換の実行であり、この変換によってGreenは図2の状態になる。
Greenに実行される行列は M であるが、Greenは親子関係のない単独のオブジェクトであるのでこの M はGreenのワールド行列である。
変換後のGreenの2つの頂点 $V_1$、$V_2$ の(ワールド)座標を求めるには、Greenに実行されているワールド行列と初期状態における $V_1$、$V_2$ の同次座標との積を計算すればよい。
プログラム10~11行目がその計算である。c_initV1、c_initV2 は初期状態における $V_1$、$V_2$ の座標を表すVector3型定数であり、V1、V2 は変換後の $V_1$、$V_2$ の座標である (ToVector4(..) は3次元ベクトルを $(x, y, z, 1)$ の形の同次座標にするカスタムライブラリーのメソッド)。
12~13行目の BallB、BallR は上記の小さな青い球、赤い球を表すオブジェクトである。この2つの球を V1、V2 に移動させると実行結果(図4)に示されるように変換後のGreenの2つの頂点に置かれることになる。
なお 12~13行目の SetWorldPosition(Vector3 v) はオブジェクトを引数で指定された分だけ平行移動させるカスタムライブラリーのメソッドであり、次の記述と同等である。
Matrix4x4 T1 = TH3DMath.GetTranslation4x4(V1); Matrix4x4 T2 = TH3DMath.GetTranslation4x4(V2); BallB.SetMatrix(T1); BallB.SetMatrix(T2);
# Code2
図5はオブジェクト Box の初期状態である。Boxは初期状態では1辺の長さが $1$ の立方体で、その中心が原点に置かれている。図中の $V_0$~$V_7$ はBoxの各頂点を表している。初期状態においてBoxの各辺は x軸、y軸、z軸に平行なので、例えば頂点 $V_0$ の座標は $(0.5,\ 0.5, -0.5)$ であり、頂点 $V_5$ の座標は $(0.5, -0.5,\ 0.5)$ である。
図6はBoxに対して適当な回転及びスケールが行われている様子である。


今回のプログラムでは上図に示される運動を行っているBoxの各頂点に、図7の小さな白い球が常に置かれるようにする (この白い球は8個あり、初期状態ではその中心が原点に置かれている)。


プログラムは以下のとおり。
[Code2] (実行結果 図8)
BoxMotion();
Matrix4x4 M = Box.GetMatrix();
for (int i = 0; i < MiniBall.Length; i++)
{
Vector3 pos = M * TH3DMath.ToVector4(c_initBoxVerts[i]);
MiniBall[i].SetWorldPosition(pos);
}
1行目の BoxMotion() はBoxを上図に示されるような運動を行わせるためのもので、毎フレーム 指定の位置における回転及びスケールがBoxに対して実行される。3行目の M はその時点で実行されているBoxの変換行列、すなわち その時点におけるBoxのワールド行列である。
プログラム中の MiniBall は上図6の小さい白い球を表すオブジェクトであり、要素数 8 の配列である。7行目はその時点におけるBoxの各頂点座標の計算であり、ここで使われている c_initBoxVerts は初期状態のBoxの各頂点 $V_0$~$V_7$ の座標である (上図5における $V_0$~$V_7$ の座標)。
計算内容はCode1と同様であり、現時点におけるBoxのワールド行列と初期状態における各頂点の同次座標との積を計算し、現時点での各頂点のワールド座標を求めるというものである。実行結果(図8)に示されるように、毎フレーム 変化するBoxの各頂点に白い球が常に置かれることになる。
# Code3
続いては親子関係を構成するオブジェクトの場合であり、ここでは以下の3つのオブジェクトが一体化して運動を行っている。図9はオブジェクト Base の初期状態であり、初期状態ではBaseの底面の中心は原点に置かれている。図10はオブジェクト Beam の初期状態である。Beamは細長い直方体であり、初期状態においてはその底面の中心が原点に置かれている。図11は先程使われた四角錐型のオブジェクト Green の初期状態である。ここでもGreenの青い頂点を $V_1$、赤い頂点を $V_2$ とする。
図12は各オブジェクトの階層構造であるが、Baseが一番上の親オブジェクト、Greenが一番下の子オブジェクトである。




今 この3つのオブジェクトが下図13に示されるような運動を行っているとする (Baseは指定の位置において適当な回転が行われた状態で静止しており、BeamはBaseの上で一定の範囲を往復回転している。また GreenはそのBeamの上面の一方の端で拡大縮小を繰り返している)。


今回は上記のように一体化した運動を行っているGreenの2つの頂点 $V_1$、$V_2$ に、Code1でも用いた青い球と赤い球が常に置かれるようにする。
プログラムは以下のとおり。
[Code3] (実行結果 図14)
Matrix4x4[] mtrcs = CalcLocalMatrices(); Matrix4x4 localGreen = mtrcs[0]; Matrix4x4 localBeam = mtrcs[1]; Matrix4x4 localBase = mtrcs[2]; Matrix4x4 worldGreen = localBase * localBeam * localGreen; Matrix4x4 worldBeam = localBase * localBeam; Matrix4x4 worldBase = localBase; Green.SetMatrix(worldGreen); Beam.SetMatrix(worldBeam); Base.SetMatrix(worldBase); Vector3 V1 = worldGreen * TH3DMath.ToVector4(c_initV1); Vector3 V2 = worldGreen * TH3DMath.ToVector4(c_initV2); BallB.SetWorldPosition(V1); BallR.SetWorldPosition(V2);
12行目までは3つのオブジェクトの一体化運動に関する記述である。3つのオブジェクトの運動自体は別の箇所に記述されており、毎フレーム CalcLocalMatrices() (1行目)によって各オブジェクトのローカル行列を取得する (返される値は Green、Beam、Base のローカル行列がセットされた配列である)。
14行目以降はCode1と同じ内容である。現時点での $V_1$ と $V_2$ のワールド座標を算出し、青い球を $V_1$ に、赤い球を $V_2$ に移動させる。これを毎フレーム行うことで実行結果(図14)に示されるように2つの球が2つの頂点に常に置かれるようになる。
# Code4
今回のプログラムでは図15のオブジェクト Cannon から指定の方向に弾を発射することについて考える。図16はCannonから発射される弾を表すオブジェクト Shell である。今回使われるShellは球体であり、初期状態においてはその中心が原点に置かれている。

Cannonは初期状態において z軸プラス方向を向いている。下図17における点 $S$ はCannonの初期状態におけるShellの発射開始位置であり、$\boldsymbol{\mathsf{v}}$ は発射方向を表す単位ベクトルである (初期状態においては発射方向 $\boldsymbol{\mathsf{v}}$ は z軸プラス方向)。


図18はCannonに適当な変換(平行移動 + 回転)を行ったときのものであるが、このときの Shell発射開始位置、及び発射方向は次のように求められる。
Code1~Code3ではGreenやBoxに適当な変換を行い、GreenやBoxの変換後の頂点座標を計算したがここでも考え方は同じである。Cannonの変換後における発射開始位置は、変換後のCannonのワールド行列と初期状態における発射開始位置 $S$ の同次座標との積を計算すればよい。
具体的には以下のように記述される。
Matrix4x4 mtx = Cannon.GetMatrix(); Vector3 shootPos = mtx * TH3DMath.ToVector4(c_initShootPosition);
mtx はCannonのワールド行列、c_initShootPosition は初期状態における発射開始位置 $S$ のことであり、shootPos が変換後の発射開始位置である。
前節の終わりで述べたように、オブジェクトに対して何らかの変換が行われ、その変換後のオブジェクトの向き(ワールド座標系における向き)を計算するには、その時点でのオブジェクトのワールド行列と初期状態におけるオブジェクトの向きを表すベクトルとの積を計算すればよい。ただし その際にはベクトルを($w = 1$ ではなく) $w = 0$ で同次座標化する必要がある。
今回の例では図18の状態におけるShellの発射方向の計算であるが、この場合には図18の時点でのCannonのワールド行列と初期状態における発射方向 $\boldsymbol{\mathsf{v}}$ との積を計算する。そしてその計算の際には $\boldsymbol{\mathsf{v}}$ を $w=0$ で同次座標化したものを使う。
具体的には以下のとおり。
Matrix4x4 mtx = Cannon.GetMatrix(); Vector4 v4 = c_initShootDirection; // w=0 Vector3 shootDir = mtx * v4;
2行目の c_initShootDirection は初期状態における発射方向 $\boldsymbol{\mathsf{v}}$ を表すVector3型の定数であり、図17に示されるようにその値は z軸プラス方向 $(0, 0, 1)$ である。v4 は $\boldsymbol{\mathsf{v}}$ を $w=0$ で同次座標化した4次元ベクトルである (UnityではVector4にVector3を代入すると自動的に w座標が $0$ になる)。3行目の shootDir が変換後のCannonの発射方向である。
なお 上の記述は次のように簡略化できる。
Matrix4x4 mtx = Cannon.GetMatrix(); Vector3 shootDir = mtx * c_initShootDirection;
2行目の mtx * c_initShootPosition は Matrix4x4 と Vector3 の積の計算である。数学的には $4\times4$行列と3次元ベクトルの積は定義されないが、Unityではこの場合 Vector3 が自動的に Vector4 に変換されて計算される。そしてその際 Vector4 の w座標に $0$ がセットされるのである。
なお本節で使用するShellはカスタムライブラリーの THShell3D 型のインスタンスであるが、THShell3D クラスにはShellの動作に関連するいくつかのプロパティが用意されている。

position
: 現在のShellのワールド座標(正確にはワールド座標系においてどれだけ平行移動が行われたか)を表すVector3型プロパティ。direction
: Shellの発射方向を表すVector3型のプロパティ (この方向にShellは飛んでいくので進行方向でもある)。speed
: Shellが1フレームあたりに進む距離 (float型)。rotMatrix
: Shellの回転状態を保持するための行列 (Matrix4x4型)。次のプログラムは上図18の状態のCannonからShellを発射するものである (Aキーを押すことでShellが発射される)。
[Code4] (実行結果 図19)
if (Input.GetKeyDown(KeyCode.A))
{
Matrix4x4 mtx = Cannon.GetMatrix();
Vector3 shootPos = mtx * TH3DMath.ToVector4(c_initShootPosition);
Vector3 shootDir = mtx * c_initShootDirection;
Shell.direction = shootDir;
Shell.speed = 0.062f;
Matrix4x4 T = TH3DMath.GetTranslation4x4(shootPos);
Shell.SetMatrix(T);
return;
}
Vector3 pos = Shell.position + Shell.speed * Shell.direction;
Matrix4x4 M = TH3DMath.GetTranslation4x4(pos);
Shell.SetMatrix(M);
1行目のifブロックには A キーが押されるたびに入るが、ここではShellの発射開始位置、及び発射方向を計算し、Shellを開始位置に移動させることまでが行われる。3~5行目は上で述べたShellの発射開始位置、及び発射方向の計算である。
7~8行目はShellのプロパティ direction、speed へのセットである。これらのプロパティの値はShellの運動中に変化することはない。
16行目以降はShellを指定の方向に毎フレーム 指定の距離だけ移動させる処理である。具体的には毎フレーム Shellの現在地(Shell.position)から Shell.direction の方向に Shell.speed だけ進んで行く。
16~18行目は毎フレーム 実行されるので A キーが押されない限り常にShellは指定の方向に進み続ける (A キーが押されるとShellは再び発射開始位置からのスタートになる)。
# Code5
Code4で使われていたShellは球体であったが、今回のプログラムでは下図20に示される細長いShellを使用する。球体と違って、このShellには向きがありShellを発射する際にはその発射方向に向いている必要がある。初期状態ではその向きは z軸プラス方向であるので図21に示されるように、Shellの向きを変えずに初期状態のCannonの発射開始位置 $S$ まで移動させると、そのまま発射できる状態になる (この場合にはShellの向きと発射方向 $\boldsymbol{\mathsf{v}}$ が一致している)。


しかし、Cannonに何らかの回転が行われている場合には事情は異なる。
例えば下図22はCannonに対して適当な変換を行い、Shellの向きを変えずに発射開始位置に移動させたものである。図に示されるように本来はShellは発射方向である $\boldsymbol{\mathsf{v}}$ を向いていなければいけないが、向きを変えていないため z軸プラス方向を向いたままになっている。
そしてこのまま発射すると(Code4をそのまま使うと)、図23のような結果、すなわち Shellが初期状態の向きと同じ z軸プラス方向を向いた状態で進んで行くことになる。


Shellの発射方向とはCannonの向いている方向のことである。ある時点でCannonが $\boldsymbol{\mathsf{v_1}}$ の方向を向いていれば、発射方向も $\boldsymbol{\mathsf{v_1}}$ であり、Shellを発射する際にはShellも $\boldsymbol{\mathsf{v_1}}$ に向ける必要がある (図24)。同様に、Cannonが $\boldsymbol{\mathsf{v_2}}$ の方向を向いていれば、発射方向も $\boldsymbol{\mathsf{v_2}}$ であり、Shell発射の際にはShellも $\boldsymbol{\mathsf{v_2}}$ に向ける必要がある (図25)。


Cannonに対してある回転 $R$ を行ったときにCannonの向きが $\boldsymbol{\mathsf{v}}$ になったとする。このとき発射方向は $\boldsymbol{\mathsf{v}}$ であるからShellを発射する際にはShellも $\boldsymbol{\mathsf{v}}$ の方向に向ける必要がある。問題はどのようにしてShellを $\boldsymbol{\mathsf{v}}$ の方向に向けるかということであるが、これは簡単に解決する。
Cannonは初期状態で z軸プラス方向を向いているので、Cannonに回転 $R$ を行ったときにCannonが $\boldsymbol{\mathsf{v}}$ を向いたということは、z軸プラス方向に回転 $R$ を実行すると $\boldsymbol{\mathsf{v}}$ の方向を向くことを意味する。ShellもCannonと同じく初期状態では z軸プラス方向を向いているので、Shellに対して回転 $R$ を行えばShellの向きは $\boldsymbol{\mathsf{v}}$ の方向に向けられるわけである。
つまり、ある時点においてShellの向きをCannonの向きと同じにするためには、そのときCannonに実行されている回転をShellに対しても実行すればよいのである。
次のプログラムはキー操作によってCannonの向きを変え、図20のShellをCannonから発射するものである。
キー操作は以下のとおり。
H、J、K、L : Cannonの向きを変える。
A : Shellの発射。
[Code5] (実行結果 図26)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L) )
{
ChangeCannonDirection();
}
if (Input.GetKeyDown(KeyCode.A))
{
Matrix4x4 mtx = Cannon.GetMatrix();
Vector3 shootPos = mtx * TH3DMath.ToVector4(c_initShootPosition);
Vector3 shootDir = mtx * c_initShootDirection;
Shell.direction = shootDir;
Shell.speed = 0.094f;
mtx.SetColumn(3, new Vector4(0, 0, 0, 1));
Shell.rotMatrix = mtx;
Matrix4x4 T = TH3DMath.GetTranslation4x4(shootPos);
Shell.SetMatrix(T * Shell.rotMatrix);
return;
}
Vector3 pos = Shell.position + Shell.speed * Shell.direction;
Matrix4x4 M = TH3DMath.GetTranslation4x4(pos) * Shell.rotMatrix;
Shell.SetMatrix(M);
1行目のifブロックはキー操作によってCannonの向きを変える処理である。
A キーが押されるたびに7行目のifブロックに入る。このifブロックではShellを発射開始位置に移動させるが、今回は移動させるだけでなく向きを発射方向に向けた状態にしている。具体的には16行目以降の部分である。
ローカル変数 mtx はその時点においてCannonに実行されている変換行列(ワールド行列)であり、Cannonには回転と平行移動しか行っていないので mtx は回転行列と平行移動行列の積である。
4-6節で述べたように変換行列の1~3列目はスケール成分と回転成分を表し、4列目は平行移動成分を表している。そして今回はCannonにはスケールを行っていないのでCannonに実行されている変換行列 mtx の1~3列目は回転成分のみであり、Cannonに実行されている回転だけを取り出すには mtx の4列目を $(0, 0, 0, 1)$ にすればよい (変換行列の第4列目が $(0, 0, 0, 1)$ であることは何も平行移動を行っていないことを意味する)。
16行目の SetColumn(..) は mtx の4列目を $(0, 0, 0, 1)$ にするための処理であり、これによって mtx はCannonに実行された回転を表す回転行列になる。17行目ではこの回転行列をShellのプロパティ rotMatrix にセットしている。Shellを発射する際にはまずCannonと同じ方向に向けてから発射開始位置に移動させるが、Cannonと同じ方向に向けるためにはこの rotMatrix を使えばよい。つまり、まず始めに rotMatrix によってCannonと同じ方向に向け、その次に発射開始位置に移動させれば今回の目的が達せられる (20行目)。

(上で使われた SetColumn(..) は指定の列の内容を書き換えるためのメソッドであり、最初の引数には列番号を指定するがその値は $0$ 始めである。つまり第1列目であれば引数には $0$ を、第4列目であれば $3$ をセットする必要がある。)
# Code6
Code4、Code5ではCannonは単独のオブジェクトとして使われていたが、Cannonが他のオブジェクトと親子関係にある場合でもShellの発射開始位置や発射方向の求め方は同じである。その例としてCannonと下図27のBatteryが親子関係を構成している場合で見ていこう。Batteryが親オブジェクトであり、Cannonが子オブジェクトである。図28はCannonをアタッチポジションに移動させたときのものであり、このときBatteryは初期状態のままである。
-
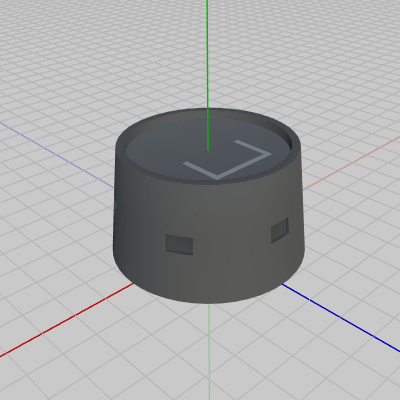 図27 Battery 初期状態
図27 Battery 初期状態 -
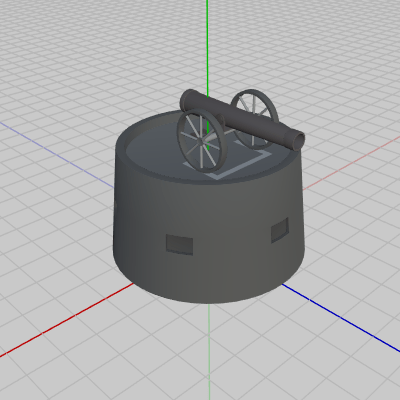 図28
図28 -
 図29 Code6 実行結果
図29 Code6 実行結果
次のプログラムはBatteryにアタッチされているCannonからShellを発射するものである。
[Code6] (実行結果 図29)
if (Input.GetKey(KeyCode.H))
{
i_degBattery -= 0.5f;
}
else if (Input.GetKey(KeyCode.L))
{
i_degBattery += 0.5f;
}
Matrix4x4 traBattery = TH3DMath.GetTranslation4x4(-8, 0, -22);
Matrix4x4 rotBattery = TH3DMath.GetRotation4x4(i_degBattery, Vector3.up);
Matrix4x4 localBattery = traBattery * rotBattery;
Matrix4x4 localCannon = TH3DMath.GetTranslation4x4(c_attachPos_Cannon);
Matrix4x4 worldCannon = localBattery * localCannon;
Matrix4x4 worldBattery = localBattery;
Cannon.SetMatrix(worldCannon);
Battery.SetMatrix(worldBattery);
if (Input.GetKeyDown(KeyCode.A))
{
Matrix4x4 mtx = Cannon.GetMatrix();
Vector3 shootPos = mtx * TH3DMath.ToVector4(c_initShootPosition);
Vector3 shootDir = mtx * c_initShootDirection;
Shell.direction = shootDir;
Shell.speed = 0.094f;
mtx.SetColumn(3, new Vector4(0, 0, 0, 1));
Shell.rotMatrix = mtx;
Matrix4x4 T = TH3DMath.GetTranslation4x4(shootPos);
Shell.SetMatrix(T * Shell.rotMatrix);
return;
}
Vector3 pos = Shell.position + Shell.speed * Shell.direction;
Matrix4x4 M = TH3DMath.GetTranslation4x4(pos) * Shell.rotMatrix;
Shell.SetMatrix(M);
このプログラムでは H あるいは L キーによってBatteryを回転させるが、i_degBattery はBatteryの回転角度を表すインスタンス変数である。10~20行目が一体化運動の記述であり、Batteryは指定の位置で回転を行い、Cannonはアタッチポジションまでの移動を行うだけである。
23行目以降はShell発射に関する処理であるが、この部分はCode5の7行目以降と同じである。
Cannonが親子階層に含まれていても、ワールド座標系におけるShellの発射開始位置や発射方向を求めるのであれば、それらはCannonのワールド行列から算出される。この点はCannonが単独のオブジェクトの場合のCode4やCode5と同じである。
# Code7
以下の2つのプログラムは読者用の課題である。今までのプログラムはすべてローカル座標をワールド座標に変換するものであった。以下の2つの課題はいずれもその逆であり、ワールド座標からローカル座標への変換である。
例えばレイとオブジェクトの衝突判定を行う場合などでは、レイの始点及びその進行方向をオブジェクトのローカル座標系の値に変換することが多い。オブジェクトが非常に多くの三角形の集合として構成されているような場合、毎フレーム1つ1つの三角形の各頂点のワールド座標を計算することは現実的ではない。これは2-15節でも同様のことを述べたが、そういった場合にはオブジェクトを構成するすべての三角形のワールド座標を求めるのではなく、レイの始点とその進行方向をオブジェクトのローカル座標系で測った値に変換して、オブジェクトのローカル座標系で衝突判定を行う方がはるかに効率的なのである (各三角形の頂点座標はメッシュの座標(初期状態の頂点座標)を使えばよい)。
下図はレイと直方体の衝突判定を行っているときの様子である。図中の $R_0$ はレイの始点、$\boldsymbol{\mathsf{v}}$ はレイの進行方向を表す単位ベクトルである。
直方体オブジェクト Box は初期状態において各辺が x軸、y軸、z軸に平行であり、その中心が原点に置かれている。

ここで $R_0$ 及び $\boldsymbol{\mathsf{v}}$ をBoxのローカル座標系で測った値に変換することを考えよう。以下 Box座標系の x軸、y軸、z軸を $\boldsymbol{lx}$、$\boldsymbol{ly}$、$\boldsymbol{lz}$ とする (下図31)。
レイの始点 $R_0$ であれば、Box座標系の原点と $R_0$ を結ぶベクトルを $\boldsymbol{\mathsf{w}}$ とし、ワールド座標系で測った $\boldsymbol{\mathsf{w}}$ の値を $\boldsymbol{\mathsf{w}} = (a, b, c)$ とする。このとき $\boldsymbol{\mathsf{w}}$ の終点が $\boldsymbol{lx}$ 軸方向、$\boldsymbol{ly}$ 軸方向、$\boldsymbol{lz}$ 軸方向にどれだけ離れているかを求めその各値を $a'$、$b'$、$c'$ とすれば、$(a',\ b',\ c')$ が $R_0$ のBox座標系における座標となるのであった (考え方は3-4節の ijk座標系の議論と同じである)。

進行方向を $\boldsymbol{\mathsf{v}}$ についても同様である。$\boldsymbol{\mathsf{v}} = (s, t, u)$ とするとき ($s$、$t$、$u$ はワールド座標系で測った値)、$\boldsymbol{\mathsf{v}}$ の始点をBox座標系の原点に移動させても $\boldsymbol{\mathsf{v}}$ の各成分は $(s, t, u)$ のまま変わらない。したがって先程の $\boldsymbol{\mathsf{w}}$ と同様に、(原点を始点とする)単位ベクトル $\boldsymbol{\mathsf{v}}$ の終点が $\boldsymbol{lx}$ 軸方向、$\boldsymbol{ly}$ 軸方向、$\boldsymbol{lz}$ 軸方向にどれだけ離れているかを求めれば、それが $\boldsymbol{\mathsf{v}}$ のBox座標系における進行方向である。
プログラムには以下の2つの定数が用意されている。
R0
: レイの始点を表すVector3型定数。v
: レイの進行方向を表すVector3型定数で単位ベクトル。この2つの定数 R0、v はいずれもワールド座標である。
プログラムは最初の段階では以下の処理が記述されている。
[Code7] (実行結果 図32)
Matrix4x4 M = Box.GetMatrix();
Vector3 loc_R0 = Vector3.zero;
Vector3 loc_v = Vector3.forward;
Vector4 rslt = LocalCollisionTest(loc_R0, loc_v);
if (rslt.w >= 0.0f)
{
Hit(rslt);
}
Boxには毎フレーム回転のみが実行されるので、プログラム実行中はBoxは同じ位置でただ回転のみを行う。1行目では毎フレーム Boxに実行されているワールド行列を取得しているが、Boxにはスケールは実行されていないのでこのワールド行列の1列目~3列目の大きさはいずれも $1$ である。
3行目、5行目の loc_R0、loc_v は、$R_0$、$\boldsymbol{\mathsf{v}}$ のBox座標系における値をセットするための変数であるが、最初の段階では適当な値がセットされている。Boxのワールド行列 M と2つの定数 R0、v をもとにして、この loc_R0、loc_v に適切な値をセットすることがここでの課題である (8行目以降の処理については変更する必要はない)。
なおこの課題においてワールド座標 R0、v をBoxのローカル座標 loc_R0、loc_v に変換する際には、Boxのワールド行列の逆行列を使ってはいけないものとする。
下図の左側の十字はレイの始点 $R_0$ の位置を示し、図中の小さな赤い球はレイの進行方向を示している (レイは $R_0$ から赤い球に向かって進んでいく)。

loc_R0、loc_v へ適切な値がセットされれば、下図に示されるように十字の位置には青い球が置かれ、そこから赤い小球に向けて黄色い直線(レイ)が引かれる (実行中はレイの開始位置も進行方向も変化しない)。
しかし loc_R0、loc_v への変換が適切でなかった場合には、青い球や黄色い直線は異なる位置に表示されることになるので注意。

# Code8
引き続きレイとオブジェクトの衝突判定における、ワールド座標からローカル座標への変換を考える。下図は今回使用する正12面体オブジェクト Blue である。今回のプログラムではBlueは同じ位置において繰り返しスケールと回転をし続ける (図35)。


ここでの課題もレイの始点 $R_0$ と進行方向 $\boldsymbol{\mathsf{v}}$ をBlueのローカル座標系で測った値に変換することである。そして今回はローカル座標への変換を行う際に、Blueのワールド行列の逆行列を使って変換を行うものとする。
上のプログラムでは逆行列を使わないという制限があったが、ここではその逆でありワールド座標からローカル座標への変換は、Blueに実行されているワールド行列の逆行列を使って変換を行うということである。
プログラムには先程と同じくレイの始点を表す R0、進行方向を表す v の2つのVector3型定数が用意されている (いずれもワールド座標)。
プログラムは最初の段階では以下の処理が記述されている。
[Code8] (実行結果 図36)
Matrix4x4 M = Blue.GetMatrix();
Matrix4x4 Inv = M.inverse;
Vector3 loc_R0 = Vector3.zero;
Vector3 loc_v = Vector3.forward;
Vector4 rslt = LocalCollisionTest(loc_R0, loc_v);
if (rslt.w >= 0.0f)
{
Hit(rslt);
}
1行目の M がBlueに実行されているワールド行列、2行目の Inv がその逆行列である。このプログラムにおいてもワールド座標 R0、v をBlue座標系のローカル座標に変換し、それぞれ loc_R0、loc_v にセットすればよい (9行目以降の処理は変更する必要はない)。

(解答例のプログラムは Sec413_Ans.txt を参照 ; Sec413_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
© 2020-2025 Redpoll's 60 (All rights reserved)