Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-2
第2章 2D空間におけるオブジェクトの運動
$§$2-2 行列による変換の詳細 1
第1章でも述べたが、この講義の第5章まではオブジェクトの変換については行列を主に使用する。行列によるオブジェクトの変換は、Unityの標準的な変換方法ではない。しかし、行列はコンピューターグラフィックス(特に3DCG)において、ベクトルと並ぶ最も重要な概念であり、コンピューターグラフィックスにおけるオブジェクトの運動は、行列的な思考を基礎にしている。つまり、コンピューターグラフィックスにおいてオブジェクトの運動を考える際には、行列を通して考えるのである。
まずは単一のオブジェクトの場合で見ていくことにしよう。
図1 Point 初期状態 (原点の小さな青い点) 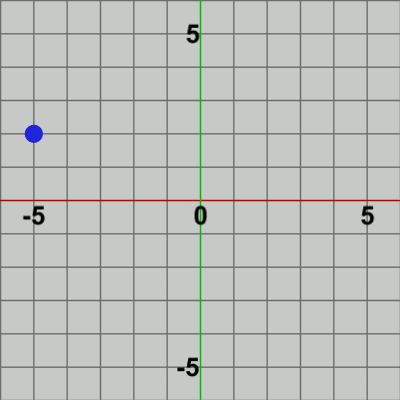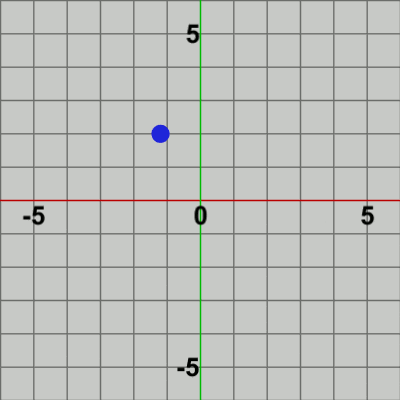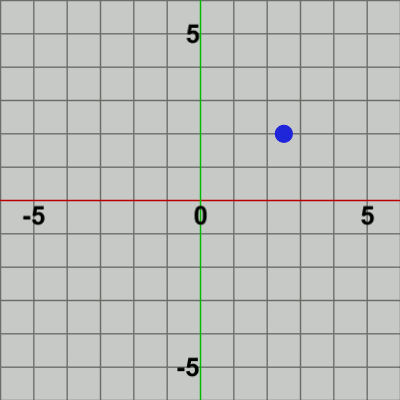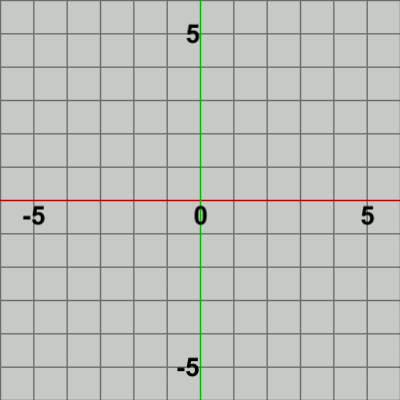
図2 Code1 実行結果
[Code1] (実行結果 図2)
1行目の i_positionは Pointの現在位置を表す Vector2型のインスタンス変数である。i_position の初期値は $(-5.1,\ 2)$ であり、最初のフレームの1行目で i_positionの内容は $(-5, 2)$ となり、2行目で i_positionだけ移動する平行移動行列Tが計算され、3行目で その行列が Pointに対して実行され、Pointが i_positionの位置に移動することになる。i_positionの値は毎フレーム変化するが、以降のフレームにおいてもこの処理が繰り返されるわけである。
1行目で i_positionは そのx成分が毎フレーム $0.1$ずつ加算されるので、Pointは毎フレームx軸方向に $0.1$ずつ進んでいくことになる。具体的には、最初のフレームでの位置は $(-5,\ 2)$、次のフレームでは $(-4.9,\ 2)$、さらに $(-4.8,\ 2)$, $(-4.7,\ 2)$, $(-4.6,\ 2)$ ... と続く。これらの座標は各フレームにおける Pointの移動位置である。
そして、ここで重要なのは、Pointは これらの位置に毎フレーム初期状態の位置から、すなわち Pointの場合は原点から移動するのである。つまり、最初のフレームで Pointは原点から $(-5,\ 2)$に移動し、次のフレームにおいても原点から $(-4.9,\ 2)$に移動し、それ以降も原点からそのフレームでの移動位置へ移動するのである。しかし、図2のアニメーションを見ればわかるように Pointは、$(-5,\ 2)$, $(-4.9,\ 2)$, $(-4.8,\ 2)$ ... と連続的に移動しており、原点から $(-5,\ 2)$、原点から $(-4.9,\ 2)$、原点から $(-4.8,\ 2)$ ... といった原点との往復運動はしていない。
それは、各フレームで描画されるオブジェクトの位置は、SetMatrix(..) を初期状態のオブジェクトに実行した結果の位置になるからである。この例では、毎フレーム Pointに対して3行目の SetMatrix(..) で実行される行列は2行目で計算される平行移動行列 T である。この平行移動行列Tの内容は、最初のフレームでは $(-5,\ 2)$だけの平行移動、次のフレームでは $(-4.9,\ 2)$だけの平行移動、さらにそれ以降においても $(-4.8,\ 2)$だけの平行移動、$(-4.7,\ 2)$だけの平行移動、$(-4.6,\ 2)$だけの平行移動 ... と続いていく。各フレームで描画されるのは、この平行移動行列Tを初期状態の Pointに実行した結果であるので、最初のフレームでは Point が原点から $(-5,\ 2)$だけ移動した位置においてフレーム描画が発生し、次のフレームでは Pointが原点から $(-4.9,\ 2)$だけ移動した位置においてフレーム描画が発生する。それ以降も同様である。
ここで述べたことを図にしたものが以下の図である。
図3 
図4
図3は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。
具体的には、図3のアニメーションにおいて赤いフィルターがかかっている状態は Pointに対して実行される平行移動行列 T を可視化したものである。つまり、赤いフィルターの状態は、平行移動行列Tを Pointに対して実行している過程なのである。そして その後、通常の色に変化するが この瞬間においてフレーム描画が発生するのである。つまり、赤いフィルター状態から通常の色に変化することは、ここでフレーム描画が発生していることを意味している。すなわち、通常色の状態は、平行移動行列Tを Pointに対して実行した結果なのである (上でも述べているように、初期状態のオブジェクトに対して変換行列を実行した結果が、フレームとして描画されるのである)。
図4は、描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである。これらのフレームを連続的に表示すれば図2のアニメーションになるというわけである (具体的には、図4のアニメーションは4FPS、図2のアニメーションは30FPSである)。
(注 : リアルタイムグラフィックスでは、フレーム描画は GPU(Graphics Processing Unit) が担当する処理であるが、フレームに描画される内容は上でも述べたように、オブジェクトに対する変換行列の実行結果のみである。図3における赤いフィルターの状態、つまり 変換行列の実行過程は GPUでのフレーム描画には含まれない。赤いフィルターの状態は、あくまで解説目的に付加されているアニメーションである)
[Code2] (実行結果 図5)
1行目、2行目はCode1と同じである (ここでも i_position の初期値は $(-5.1,\ 2)$ であり、最初のフレームで $(-5, 2)$ になる)。3行目の$3\times3$行列 Upは、y軸方向に $1$だけ移動させる平行移動行列であり、4行目の$3\times3$行列 Downは、y軸方向に $-1$だけ移動させる平行移動行列である (プログラムからわかるように Up、Downは毎フレーム同じ内容である)。
5行目の3つの行列の積は、3つの平行移動の合成を表している。すなわち、まず y軸方向に $1$の移動、次に y軸方向に $-1$の移動、最後に i_positionへの移動 という順序で3つの平行移動が行われる。最初の2つの平行移動は、y軸方向に $1$移動して、$-1$移動するというものなので、Pointの場合、結局は元の位置である原点に戻ることになる。第3の変換は1行目、2行目で算出される平行移動行列 T であるが、この部分はCode1と全く同じなので、毎フレーム算出されるTの内容もCode1と同じものである。
図5 Code2 実行結果 (Code1と同じ結果) したがって、y軸方向に $1$の移動(Up)、次に y軸方向に $-1$の移動(Down)、そして平行移動行列Tによる i_positionへの移動は、結局は毎フレーム、原点から i_positionへの移動の繰り返しであり、つまり これはCode1と同じである (Code2において Pointに実行される変換行列は Up、Down、T の積Mであるが、上の説明から結局 このMの内容はTに等しい)。もちろん、実行結果もCode1と同じである。
プログラムの実行結果である図5を見ればわかるように、各フレームに描画されるオブジェクトの位置は Code1と同様に $(-5,\ 2)$を開始点として、$(-4.9,\ 2)$, $(-4.8,\ 2)$, $(-4.7,\ 2)$ ... と連続的に移動している。
y軸方向に上がって下がるといった運動はプログラム上では存在するが、実際の実行結果には現れていない。それは 上でも述べたように、各フレームで描画されるオブジェクトの位置は、初期状態のオブジェクトに変換行列を実行した結果の位置になるためである。
Pointに対して実行される変換行列は Code1では T、Code2では Mである。Mは、M = T * Down * Up (5行目)と算出されるが、先ほども述べたように、その内容はTと同じものである。各フレームに描画されるオブジェクトの位置は変換行列を実行した結果の位置であるので、その行列の算出過程が異なっていても算出される行列の内容が同じであれば、各フレームに描画されるオブジェクトの位置は同じになるのである。
Code1とCode2では Pointに実行される変換行列の算出過程は異なるが、算出される行列の内容は各フレームで同じであるので、Pointが描画される位置も各フレームで同じであり、実行結果も同じものになるのである。
図6 図6は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。
赤いフィルターがかかっている状態は Pointに対して変換行列Mを実行している過程である。Mは Up、Down、T の積であり、変換もこの順序で行われる。実際に、図6を見れば Pointは原点からy軸方向に$1$移動し、次に y軸方向に$-1$移動(原点に戻る)、最後に原点から i_positionへの移動が行われている。i_positionに移動した時点で、赤いフィルターの状態から通常の色に変化するが、このときにフレームの描画が発生する。つまり、通常色の状態は Pointに対して変換行列Mを実行した結果なのである。
描画されるフレームを連続的に表示すれば図5のアニメーションになる。
繰り返しになるが、初期状態のオブジェクトに対して変換行列を実行した結果がフレームとして描画されるのである (Code1、Code2の場合では「初期状態のオブジェクト」は原点に置かれているPointである)。
使用するプログラムは、1-10節のCode4と同じものであり、図7のオブジェクト Diskに対して回転を実行するだけのプログラムである。
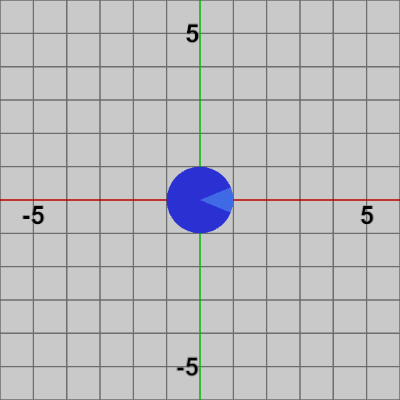
図7 Disk 初期状態 
図8 Code3 実行結果
[Code3] (実行結果 図8)
1行目の i_degree は、Diskの回転角度を表す float型のインスタンス変数である。初期値は $0$なので、最初のフレームで加算代入されて$5$となり、次のフレームにおいて$10$、以降も同様に $15$, $20$, $25$ ... と増加していく。つまり、Diskは最初のフレームにおいて$5$°回転、次のフレームにおいて$10$°回転、さらにその次のフレームにおいて$15$°回転 ... といった処理が毎フレーム行われるわけである (Unityにおいて XY平面における回転は反時計周りが回転のプラス方向である)。
そして、平行移動の場合と同様に、Diskに対して行われるこれらの回転は 毎フレーム初期状態の向きから、すなわち Diskの場合は明るい青色の部分がx軸プラス方向を向いている状態(図7)から行われるのである。具体的には、明るい青色の部分がx軸プラス方向を向いている状態(Diskの初期状態)を回転角度 $0$°とするのである。
つまり、最初のフレームで Diskは初期状態の向きから$5$°回転し、次のフレームで初期状態の向きから$10$°回転、さらにその次のフレームで初期状態の向きから$15$°回転 ... といった具合に毎フレーム i_degree で表される角度の回転が初期状態の向きから行われる。
しかし、実行結果(図8)を見ればわかるように Diskの回転は連続的に行われており、初期状態の向きから$5$°回転、初期状態の向きから$10$°回転、初期状態の向きから$15$°回転 ... といった初期状態の向きと そのフレームでの回転角度との間の往復運動は見られない。
もちろん、これは平行移動の箇所で述べてきた事情と同じことによるものである。平行移動の場合は、各フレームで描画されるオブジェクトの位置は、初期状態のオブジェクトに変換行列を実行した結果の位置であったが、それと同様に回転の場合でも各フレームで描画されるオブジェクトの向きは、初期状態のオブジェクトに変換行列を実行した結果の向きになるのである。

図9 この例では、毎フレーム Diskに対して3行目の SetMatrix(..) で変換行列が実行されるが、その内容は2行目で計算される回転行列 R である。この回転行列Rの内容は、最初のフレームでは$5$°の回転、次のフレームで$10$°の回転、さらにその次のフレームで$15$°の回転 ... と続くが、各フレームで描画されるのは、この回転行列Rを初期状態の Diskに実行した結果であるので、最初のフレームでは Diskが初期状態から$5$°回転した状態においてフレーム描画が発生し、次のフレームでは Diskが初期状態から$10$°回転した状態においてフレーム描画が発生する。それ以降も同様である。
図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。
赤いフィルターがかかっている状態は Diskに対して実行される変換行列Rの実行過程である。図9では Diskは初期状態の向きから角度i_degreeだけ回転が行われ、回転が行われた時点で赤いフィルターの状態から通常の色に変化するが、この瞬間が実行結果の状態であり、この瞬間においてフレーム描画が発生するのである。
描画されたフレームを連続的に表示したものが図8のアニメーションである。
繰り返しになるが、オブジェクトに対して実行される変換行列は、毎フレーム 初期状態のオブジェクトに対して実行されるのである。そして、変換行列を初期状態のオブジェクトに対して実行した結果が、フレームとして描画されるのである。
オブジェクトに対して実行される変換がいくつあっても (変換行列の積がいくつあっても)、フレームとして描画されるのは、それらすべての変換を順番に実行した結果である (すなわち すべての変換行列の積を実行した結果)。
[Code4] (実行結果 図10)
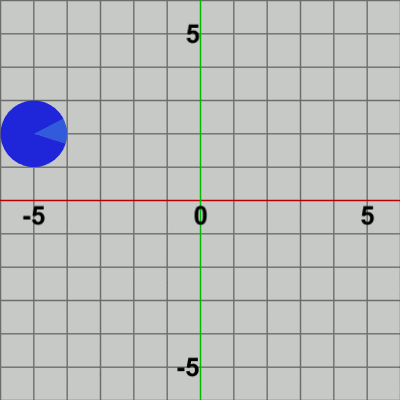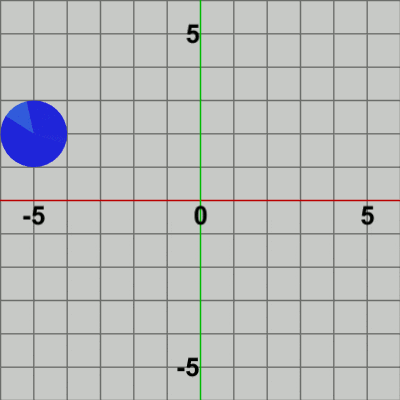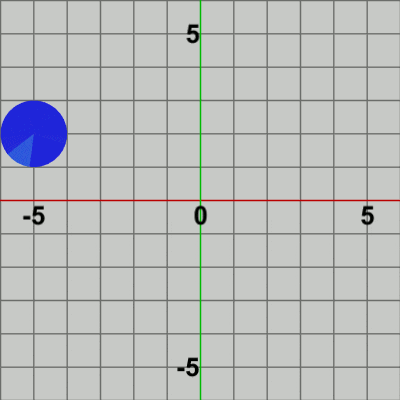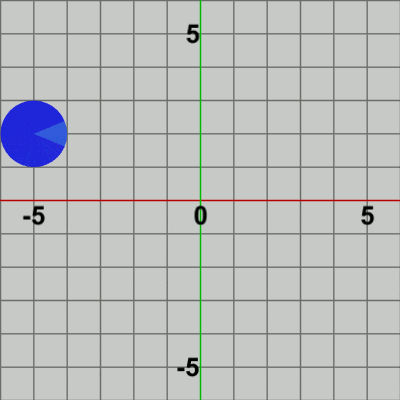
図10 Code4 実行結果 プログラムの1行目、2行目はCode3と同じである。3行目では $(-5, 2)$ だけの平行移動を実行する行列Tを取得している。4行目の行列 M = T * R は、角度i_degreeの回転(R) と $(-5, 2)$だけの平行移動(T) という2つの変換を1つにまとめたものである (変換の順序は回転、平行移動の順である)。5行目でDiskに対して このMを実行するが、このMによって Diskは初期状態から角度i_degreeだけ回転し、回転した状態で次の変換である (-5, 2) だけの平行移動が行われる。この処理が毎フレーム繰り返されることによって、Disk(の中心)が (-5, 2) の位置で回転するようになるのである (図10)。
図11は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。

図11 赤いフィルターがかかっている状態は Diskに対して実行される変換行列Mの実行過程である。最初のフレームでは、初期状態の向きから$5$°回転し、$5$°回転した状態で $(-5, 2)$ だけの平行移動が行われる。この移動が終わった時点で赤いフィルターの状態から通常の色に変化するが、この瞬間にフレーム描画が発生する (通常色の状態は変換行列MをDiskに実行した結果の状態である)。次のフレームでは、初期状態の向きから$10$°回転し、$10$°回転した状態で $(-5, 2)$ だけの平行移動が行われる。ここでも、この移動が終わった時点で通常の色に変化し、フレーム描画が発生する。さらにその次のフレームも同様である。初期状態の向きから$15$°回転し、$15$°回転した状態で $(-5, 2)$ だけの平行移動が行われ、移動が終わった時点で通常の色に変化しフレーム描画が発生する。これ以降も同様の処理が繰り返される。
Diskの回転角度を表す i_degreeは1フレームあたり$5$°ずつ回転するので$360$°回転するまでに72フレーム必要になる。Code4の実行結果である図10(及び Code3の実行結果である図8)のアニメーションは、上述の手順によって描画された72枚のフレームを連続的に表示しているのである (約30FPS)。
しかし、もし平行移動行列Tの内容を毎フレーム変化させ、Diskの移動先が毎フレーム異なる位置になるのであれば、Diskの回転は移動しながらの回転となる。今回作成するのはそういったプログラムである。
[Code5] (実行結果 図12)
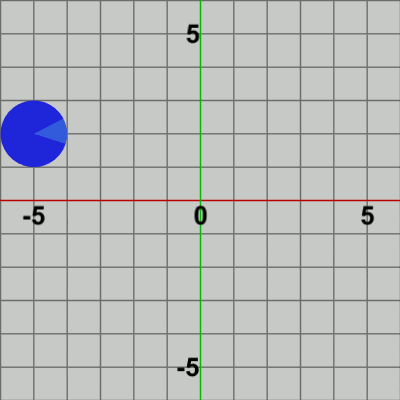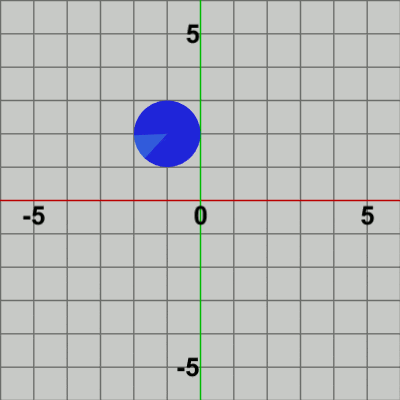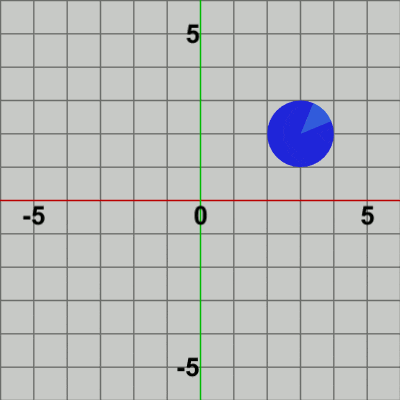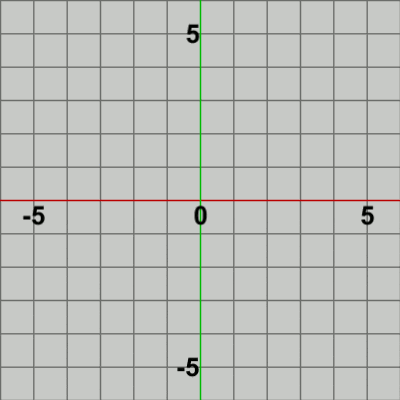
図12 Code5 実行結果 1行目、2行目はCode3と同じであり、3行目、4行目はCode1と同じである。このプログラムはCode4における平行移動行列Tの内容が毎フレーム変化するようにしただけのものである。
i_degreeは1行目で毎フレーム$5$ずつ増加する。最初のフレームでは $5$、次のフレームで $10$、それ以降も $15$, $20$, $25$ ... と増加していく。i_positionは、そのx成分が3行目で$0.1$ずつ増加する。i_position自体の値は最初のフレームでは $(-5,\ 2)$、次のフレームで $(-4.9,\ 2)$、それ以降も $(-4.8,\ 2)$, $(-4.7,\ 2)$, $(-4.6,\ 2)$ ... と変化する (これらのことは今までのプログラムでも同様である)。
2行目の回転行列Rや4行目の平行移動行列Tも今までのものと同様に、Rはi_degreeだけ回転させる行列であり、Tはi_positionだけ平行移動させる行列である。そして、それらの積であるMを6行目で初期状態の Diskに対して実行するが、このMの実行によって Diskは、初期状態の向きからi_degreeだけ回転し、回転した状態で(初期状態の位置である)原点からi_positionだけ平行移動する。この処理が毎フレーム繰り返されることになる。Code4と異なり、平行移動行列Tの内容は毎フレーム変化し、Diskの移動先の位置も毎フレーム異なるので実行結果(図12)に見られるように、Diskは移動しながら回転することになるのである。
図13は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。図14は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図12のアニメーションである)。

図13 
図14
上でも述べたように、このプログラムは前回のCode4と比べて変更箇所は1箇所しかない。それは、平行移動の移動先がCode4では毎フレーム同じ位置であったのに対し、今回のプログラムでは毎フレーム異なるという点である。
図13における赤いフィルターがかかっている状態は、例によって Diskに実行される変換行列Mの実行過程である。最初のフレームでは、Diskは初期状態の向きから$5$°回転し、$5$°回転した状態で(初期状態の位置である)原点から $(-5,\ 2)$ だけ移動する。次のフレームでは、初期状態の向きから$10$°回転し、$10$°回転した状態で平行移動が行われるが、このフレームでの移動量は $(-4.9,\ 2)$ である。さらにその次のフレームでは、初期状態の向きから$15$°回転し、$15$°回転した状態で平行移動が行われるが、このフレームでの移動量は $(-4.8,\ 2)$ である。これ以降のフレームでも同様に、回転角度は $20$, $25$, $30$ ... と変化していき、平行移動の移動量は $(-4.7,\ 2)$, $(-4.6,\ 2)$, $(-4.5,\ 2)$ ... と変化していく。これによって、Diskは移動しながら回転をすることになるのである。
図11と図13を比べれば明らかであるが、各フレームにおいてどちらも回転までは同じである。つまり、初期状態の向きから角度i_degreeだけ回転させるところまでは同じであるが、その次の変換である平行移動が図11(Code4)の場合は毎フレーム同じ $(-5,\ 2)$ へ移動するのに対し、図13(Code5)での移動先は毎フレーム変化する i_position への移動となる。この違いが、同じ位置での回転になるか、あるいは 移動しながらの回転になるか ということにつながっていくのである。
本節では、オブジェクトに対して変換行列を実行することについて やや詳しく見てきた。何度も同じような説明をしたために、くどいと思われる部分もあったかもしれないが、変換行列によってオブジェクトを変換することは、コンピューターグラフィックスにおいてオブジェクトを動かす際の最も重要な基礎となる部分であるため、繰り返し強調する形をとった。
本節では2D空間において最も単純な2Dオブジェクトを用いた運動を扱ったが、変換行列によってオブジェクトを運動させる原理は、2D空間であれ3D空間であれ変わることはない。すなわち、ここで解説した事柄は、3D空間において3Dオブジェクトを運動させる場合にも同じように適用することができるのである。
まずは単一のオブジェクトの場合で見ていくことにしよう。
# Code1
第1のプログラムは、図1に示されるオブジェクトPoint(原点の小さな青い点)の平行移動である。Pointは初期状態で原点に位置しており、プログラムを実行すると、$(-5, 2)$を開始位置として、x軸方向に毎フレーム $0.1$ずつ平行移動する。

[Code1] (実行結果 図2)
i_position.x += 0.10f; THMatrix3x3 T = TH2DMath.GetTranslation3x3(i_position); Point.SetMatrix(T);
1行目の i_positionは Pointの現在位置を表す Vector2型のインスタンス変数である。i_position の初期値は $(-5.1,\ 2)$ であり、最初のフレームの1行目で i_positionの内容は $(-5, 2)$ となり、2行目で i_positionだけ移動する平行移動行列Tが計算され、3行目で その行列が Pointに対して実行され、Pointが i_positionの位置に移動することになる。i_positionの値は毎フレーム変化するが、以降のフレームにおいてもこの処理が繰り返されるわけである。
1行目で i_positionは そのx成分が毎フレーム $0.1$ずつ加算されるので、Pointは毎フレームx軸方向に $0.1$ずつ進んでいくことになる。具体的には、最初のフレームでの位置は $(-5,\ 2)$、次のフレームでは $(-4.9,\ 2)$、さらに $(-4.8,\ 2)$, $(-4.7,\ 2)$, $(-4.6,\ 2)$ ... と続く。これらの座標は各フレームにおける Pointの移動位置である。
そして、ここで重要なのは、Pointは これらの位置に毎フレーム初期状態の位置から、すなわち Pointの場合は原点から移動するのである。つまり、最初のフレームで Pointは原点から $(-5,\ 2)$に移動し、次のフレームにおいても原点から $(-4.9,\ 2)$に移動し、それ以降も原点からそのフレームでの移動位置へ移動するのである。しかし、図2のアニメーションを見ればわかるように Pointは、$(-5,\ 2)$, $(-4.9,\ 2)$, $(-4.8,\ 2)$ ... と連続的に移動しており、原点から $(-5,\ 2)$、原点から $(-4.9,\ 2)$、原点から $(-4.8,\ 2)$ ... といった原点との往復運動はしていない。
それは、各フレームで描画されるオブジェクトの位置は、SetMatrix(..) を初期状態のオブジェクトに実行した結果の位置になるからである。この例では、毎フレーム Pointに対して3行目の SetMatrix(..) で実行される行列は2行目で計算される平行移動行列 T である。この平行移動行列Tの内容は、最初のフレームでは $(-5,\ 2)$だけの平行移動、次のフレームでは $(-4.9,\ 2)$だけの平行移動、さらにそれ以降においても $(-4.8,\ 2)$だけの平行移動、$(-4.7,\ 2)$だけの平行移動、$(-4.6,\ 2)$だけの平行移動 ... と続いていく。各フレームで描画されるのは、この平行移動行列Tを初期状態の Pointに実行した結果であるので、最初のフレームでは Point が原点から $(-5,\ 2)$だけ移動した位置においてフレーム描画が発生し、次のフレームでは Pointが原点から $(-4.9,\ 2)$だけ移動した位置においてフレーム描画が発生する。それ以降も同様である。
ここで述べたことを図にしたものが以下の図である。


図3は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。
具体的には、図3のアニメーションにおいて赤いフィルターがかかっている状態は Pointに対して実行される平行移動行列 T を可視化したものである。つまり、赤いフィルターの状態は、平行移動行列Tを Pointに対して実行している過程なのである。そして その後、通常の色に変化するが この瞬間においてフレーム描画が発生するのである。つまり、赤いフィルター状態から通常の色に変化することは、ここでフレーム描画が発生していることを意味している。すなわち、通常色の状態は、平行移動行列Tを Pointに対して実行した結果なのである (上でも述べているように、初期状態のオブジェクトに対して変換行列を実行した結果が、フレームとして描画されるのである)。
図4は、描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである。これらのフレームを連続的に表示すれば図2のアニメーションになるというわけである (具体的には、図4のアニメーションは4FPS、図2のアニメーションは30FPSである)。
(注 : リアルタイムグラフィックスでは、フレーム描画は GPU(Graphics Processing Unit) が担当する処理であるが、フレームに描画される内容は上でも述べたように、オブジェクトに対する変換行列の実行結果のみである。図3における赤いフィルターの状態、つまり 変換行列の実行過程は GPUでのフレーム描画には含まれない。赤いフィルターの状態は、あくまで解説目的に付加されているアニメーションである)
# Code2
上のプログラムに関連して次のプログラムを考える。[Code2] (実行結果 図5)
i_position.x += 0.10f; THMatrix3x3 T = TH2DMath.GetTranslation3x3(i_position); THMatrix3x3 Up = TH2DMath.GetTranslation3x3(0, 1); THMatrix3x3 Down = TH2DMath.GetTranslation3x3(0, -1); THMatrix3x3 M = T * Down * Up; Point.SetMatrix(M);
1行目、2行目はCode1と同じである (ここでも i_position の初期値は $(-5.1,\ 2)$ であり、最初のフレームで $(-5, 2)$ になる)。3行目の$3\times3$行列 Upは、y軸方向に $1$だけ移動させる平行移動行列であり、4行目の$3\times3$行列 Downは、y軸方向に $-1$だけ移動させる平行移動行列である (プログラムからわかるように Up、Downは毎フレーム同じ内容である)。
5行目の3つの行列の積は、3つの平行移動の合成を表している。すなわち、まず y軸方向に $1$の移動、次に y軸方向に $-1$の移動、最後に i_positionへの移動 という順序で3つの平行移動が行われる。最初の2つの平行移動は、y軸方向に $1$移動して、$-1$移動するというものなので、Pointの場合、結局は元の位置である原点に戻ることになる。第3の変換は1行目、2行目で算出される平行移動行列 T であるが、この部分はCode1と全く同じなので、毎フレーム算出されるTの内容もCode1と同じものである。

プログラムの実行結果である図5を見ればわかるように、各フレームに描画されるオブジェクトの位置は Code1と同様に $(-5,\ 2)$を開始点として、$(-4.9,\ 2)$, $(-4.8,\ 2)$, $(-4.7,\ 2)$ ... と連続的に移動している。
y軸方向に上がって下がるといった運動はプログラム上では存在するが、実際の実行結果には現れていない。それは 上でも述べたように、各フレームで描画されるオブジェクトの位置は、初期状態のオブジェクトに変換行列を実行した結果の位置になるためである。
Pointに対して実行される変換行列は Code1では T、Code2では Mである。Mは、M = T * Down * Up (5行目)と算出されるが、先ほども述べたように、その内容はTと同じものである。各フレームに描画されるオブジェクトの位置は変換行列を実行した結果の位置であるので、その行列の算出過程が異なっていても算出される行列の内容が同じであれば、各フレームに描画されるオブジェクトの位置は同じになるのである。
Code1とCode2では Pointに実行される変換行列の算出過程は異なるが、算出される行列の内容は各フレームで同じであるので、Pointが描画される位置も各フレームで同じであり、実行結果も同じものになるのである。

赤いフィルターがかかっている状態は Pointに対して変換行列Mを実行している過程である。Mは Up、Down、T の積であり、変換もこの順序で行われる。実際に、図6を見れば Pointは原点からy軸方向に$1$移動し、次に y軸方向に$-1$移動(原点に戻る)、最後に原点から i_positionへの移動が行われている。i_positionに移動した時点で、赤いフィルターの状態から通常の色に変化するが、このときにフレームの描画が発生する。つまり、通常色の状態は Pointに対して変換行列Mを実行した結果なのである。
描画されるフレームを連続的に表示すれば図5のアニメーションになる。
繰り返しになるが、初期状態のオブジェクトに対して変換行列を実行した結果がフレームとして描画されるのである (Code1、Code2の場合では「初期状態のオブジェクト」は原点に置かれているPointである)。
# Code3
次は、オブジェクトの回転運動である。使用するプログラムは、1-10節のCode4と同じものであり、図7のオブジェクト Diskに対して回転を実行するだけのプログラムである。


[Code3] (実行結果 図8)
i_degree += 5; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degree); Disk.SetMatrix(R);
1行目の i_degree は、Diskの回転角度を表す float型のインスタンス変数である。初期値は $0$なので、最初のフレームで加算代入されて$5$となり、次のフレームにおいて$10$、以降も同様に $15$, $20$, $25$ ... と増加していく。つまり、Diskは最初のフレームにおいて$5$°回転、次のフレームにおいて$10$°回転、さらにその次のフレームにおいて$15$°回転 ... といった処理が毎フレーム行われるわけである (Unityにおいて XY平面における回転は反時計周りが回転のプラス方向である)。
そして、平行移動の場合と同様に、Diskに対して行われるこれらの回転は 毎フレーム初期状態の向きから、すなわち Diskの場合は明るい青色の部分がx軸プラス方向を向いている状態(図7)から行われるのである。具体的には、明るい青色の部分がx軸プラス方向を向いている状態(Diskの初期状態)を回転角度 $0$°とするのである。
つまり、最初のフレームで Diskは初期状態の向きから$5$°回転し、次のフレームで初期状態の向きから$10$°回転、さらにその次のフレームで初期状態の向きから$15$°回転 ... といった具合に毎フレーム i_degree で表される角度の回転が初期状態の向きから行われる。
しかし、実行結果(図8)を見ればわかるように Diskの回転は連続的に行われており、初期状態の向きから$5$°回転、初期状態の向きから$10$°回転、初期状態の向きから$15$°回転 ... といった初期状態の向きと そのフレームでの回転角度との間の往復運動は見られない。
もちろん、これは平行移動の箇所で述べてきた事情と同じことによるものである。平行移動の場合は、各フレームで描画されるオブジェクトの位置は、初期状態のオブジェクトに変換行列を実行した結果の位置であったが、それと同様に回転の場合でも各フレームで描画されるオブジェクトの向きは、初期状態のオブジェクトに変換行列を実行した結果の向きになるのである。

図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。
赤いフィルターがかかっている状態は Diskに対して実行される変換行列Rの実行過程である。図9では Diskは初期状態の向きから角度i_degreeだけ回転が行われ、回転が行われた時点で赤いフィルターの状態から通常の色に変化するが、この瞬間が実行結果の状態であり、この瞬間においてフレーム描画が発生するのである。
描画されたフレームを連続的に表示したものが図8のアニメーションである。
繰り返しになるが、オブジェクトに対して実行される変換行列は、毎フレーム 初期状態のオブジェクトに対して実行されるのである。そして、変換行列を初期状態のオブジェクトに対して実行した結果が、フレームとして描画されるのである。
オブジェクトに対して実行される変換がいくつあっても (変換行列の積がいくつあっても)、フレームとして描画されるのは、それらすべての変換を順番に実行した結果である (すなわち すべての変換行列の積を実行した結果)。
# Code4
Code3では Diskの回転は初期状態の位置である原点において行われていた。ここでは、Diskを原点以外の場所で回転させるプログラムを作成する。[Code4] (実行結果 図10)
i_degree += 5; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degree); THMatrix3x3 T = TH2DMath.GetTranslation3x3(-5, 2); THMatrix3x3 M = T * R; Disk.SetMatrix(M);

図11は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。

Diskの回転角度を表す i_degreeは1フレームあたり$5$°ずつ回転するので$360$°回転するまでに72フレーム必要になる。Code4の実行結果である図10(及び Code3の実行結果である図8)のアニメーションは、上述の手順によって描画された72枚のフレームを連続的に表示しているのである (約30FPS)。
# Code5
Code4においては Diskは常に同じ位置で回転をしていた。Code4で Diskに実行される変換行列Mは、回転行列Rと平行移動行列Tの積であり、DiskにMを実行することは、DiskにRとTをこの順序で実行することを意味する。Code4では、回転角度を表すインスタンス変数i_degreeは毎フレーム$5$ずつ増加するので、回転行列Rの内容も毎フレーム変化するが、平行移動行列Tの内容は毎フレーム $(-5, 2)$だけの移動 であり、これはプログラム実行中ずっと変わらない。そのために、Code4では Diskは毎フレーム原点から $(-5, 2)$ へ移動し、結果として $(-5, 2)$ において回転し続けることになるのである。しかし、もし平行移動行列Tの内容を毎フレーム変化させ、Diskの移動先が毎フレーム異なる位置になるのであれば、Diskの回転は移動しながらの回転となる。今回作成するのはそういったプログラムである。
[Code5] (実行結果 図12)
i_degree += 5; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degree); i_position.x += 0.10f; THMatrix3x3 T = TH2DMath.GetTranslation3x3(i_position); THMatrix3x3 M = T * R; Disk.SetMatrix(M);

i_degreeは1行目で毎フレーム$5$ずつ増加する。最初のフレームでは $5$、次のフレームで $10$、それ以降も $15$, $20$, $25$ ... と増加していく。i_positionは、そのx成分が3行目で$0.1$ずつ増加する。i_position自体の値は最初のフレームでは $(-5,\ 2)$、次のフレームで $(-4.9,\ 2)$、それ以降も $(-4.8,\ 2)$, $(-4.7,\ 2)$, $(-4.6,\ 2)$ ... と変化する (これらのことは今までのプログラムでも同様である)。
2行目の回転行列Rや4行目の平行移動行列Tも今までのものと同様に、Rはi_degreeだけ回転させる行列であり、Tはi_positionだけ平行移動させる行列である。そして、それらの積であるMを6行目で初期状態の Diskに対して実行するが、このMの実行によって Diskは、初期状態の向きからi_degreeだけ回転し、回転した状態で(初期状態の位置である)原点からi_positionだけ平行移動する。この処理が毎フレーム繰り返されることになる。Code4と異なり、平行移動行列Tの内容は毎フレーム変化し、Diskの移動先の位置も毎フレーム異なるので実行結果(図12)に見られるように、Diskは移動しながら回転することになるのである。
図13は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。図14は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図12のアニメーションである)。


上でも述べたように、このプログラムは前回のCode4と比べて変更箇所は1箇所しかない。それは、平行移動の移動先がCode4では毎フレーム同じ位置であったのに対し、今回のプログラムでは毎フレーム異なるという点である。
図13における赤いフィルターがかかっている状態は、例によって Diskに実行される変換行列Mの実行過程である。最初のフレームでは、Diskは初期状態の向きから$5$°回転し、$5$°回転した状態で(初期状態の位置である)原点から $(-5,\ 2)$ だけ移動する。次のフレームでは、初期状態の向きから$10$°回転し、$10$°回転した状態で平行移動が行われるが、このフレームでの移動量は $(-4.9,\ 2)$ である。さらにその次のフレームでは、初期状態の向きから$15$°回転し、$15$°回転した状態で平行移動が行われるが、このフレームでの移動量は $(-4.8,\ 2)$ である。これ以降のフレームでも同様に、回転角度は $20$, $25$, $30$ ... と変化していき、平行移動の移動量は $(-4.7,\ 2)$, $(-4.6,\ 2)$, $(-4.5,\ 2)$ ... と変化していく。これによって、Diskは移動しながら回転をすることになるのである。
図11と図13を比べれば明らかであるが、各フレームにおいてどちらも回転までは同じである。つまり、初期状態の向きから角度i_degreeだけ回転させるところまでは同じであるが、その次の変換である平行移動が図11(Code4)の場合は毎フレーム同じ $(-5,\ 2)$ へ移動するのに対し、図13(Code5)での移動先は毎フレーム変化する i_position への移動となる。この違いが、同じ位置での回転になるか、あるいは 移動しながらの回転になるか ということにつながっていくのである。
本節では、オブジェクトに対して変換行列を実行することについて やや詳しく見てきた。何度も同じような説明をしたために、くどいと思われる部分もあったかもしれないが、変換行列によってオブジェクトを変換することは、コンピューターグラフィックスにおいてオブジェクトを動かす際の最も重要な基礎となる部分であるため、繰り返し強調する形をとった。
本節では2D空間において最も単純な2Dオブジェクトを用いた運動を扱ったが、変換行列によってオブジェクトを運動させる原理は、2D空間であれ3D空間であれ変わることはない。すなわち、ここで解説した事柄は、3D空間において3Dオブジェクトを運動させる場合にも同じように適用することができるのである。
© 2020-2025 Redpoll's 60 (All rights reserved)