Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-28
第2章 2D空間におけるオブジェクトの運動
$§$2-28 その他の重要事項 2 (画面に表示されるXY平面の範囲 ; ミニマップの実装)
本節ではまず実行結果の画面上に表示される2D空間の範囲、すなわち画面上にはXY平面のどこからどこまでが表示されるのかについて、続いて画面上のスクリーン座標とワールド座標の変換(ここでのワールド座標とはXY平面上の座標のことである)、最後に画面上へのミニマップの配置といった順で進められる。
今までに2D空間で扱ってきた内容では前節のカメラ移動を除いて、オブジェクトの移動はXY平面上に限定されており、したがって オブジェクトの移動では x座標、y座標のみが変化した。これは2D空間であるから当然といえば当然であるが、本節においてはオブジェクトの位置を設定するにあたって、z座標を含めて考える。今まではほとんど触れることがなかったが、本節で扱う内容においてはこの z座標の設定が非常に重要な役割を担うのである。
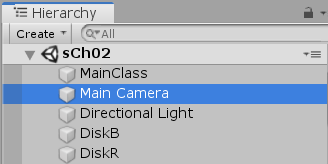
図 Hierarchyにおいて「Main Camera」を選択する しかし始める前にいくつか設定の確認をしておく必要がある。それはカメラの投影モードが「Perspective」になっているか、そしてカメラの Field of View (以下FOVと表記する)の値が「$60^\circ$」に設定されているか、さらに画面のアスペクト比が「$16:9$」であるかの3点である (これらの設定値でない場合には以下の議論において成り立たない部分が出てくるので注意)。
カメラの投影モード及びFOVの確認は、まずHierarchy Viewにおいて「Main Camera」を選択し(右図)、カメラ関連の情報をInspector上に表示する。Inspector内に表示されているいくつかの項目の中に「Projection」及び「Field of View」という項目があるので、それぞれの設定値が「Perspective」及び「$60^\circ$」であることを確認する (図1)。
画面のアスペクト比は「Game タブ」のすぐ下に表示されている数値の比である (図2)。
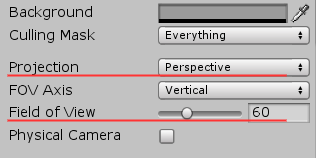
図1 「Projection : Perspective」及び「Field of View : 60°」 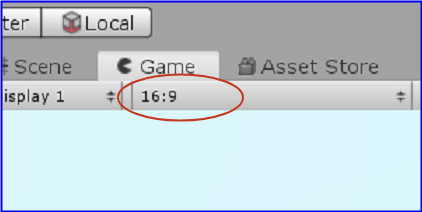
図2 アスペクト比 16:9
(Unityにおいてプロジェクト作成の際に「3D」を選択している場合は、投影モードとFOVはデフォルトで上記の「Perspective」及び「$60^\circ$」に設定されている)
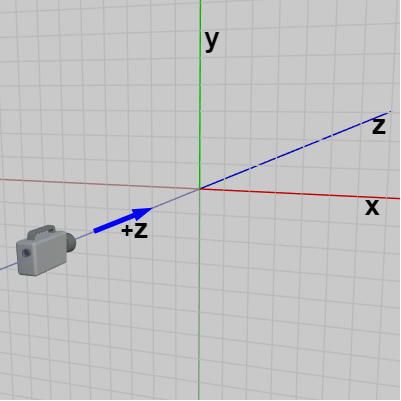
図3 カメラは z軸マイナス側に置かれ、z軸プラス方向を向いている 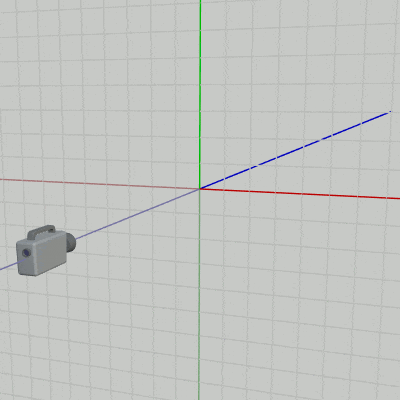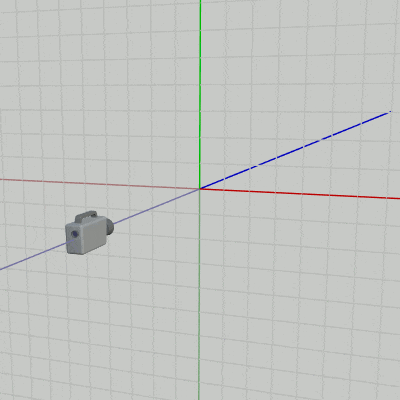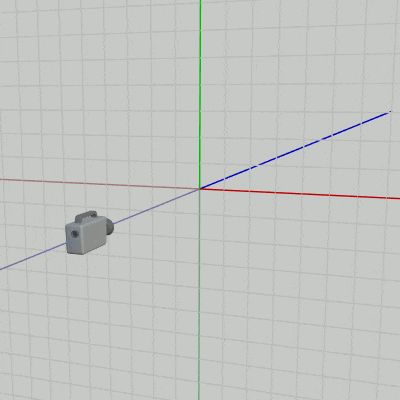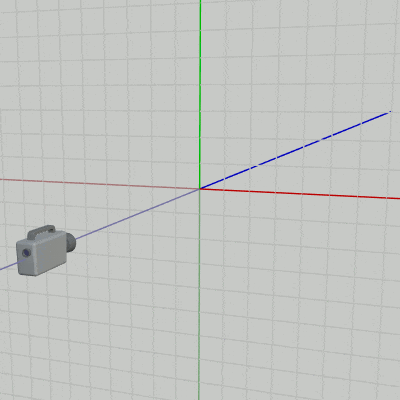
図4 z軸上でカメラを動かしているときの様子
図4ではカメラの位置を z軸上で動かして、XY平面からカメラを近づけたり離したりしているが、このときの実行結果の画面が図5である。図に示されるようにカメラをXY平面に近づけると画面に表示される範囲が狭くなり、XY平面から遠ざけると画面に表示される範囲が広がっていく。
(この例ではカメラの位置は z軸上、つまりその x座標、y座標がともに $0$ であるが、以下の解説においてもしばらくの間はこの設定で進める。すなわちカメラの位置は z軸上にあるものとし、実行結果の画面中心には原点が来る)
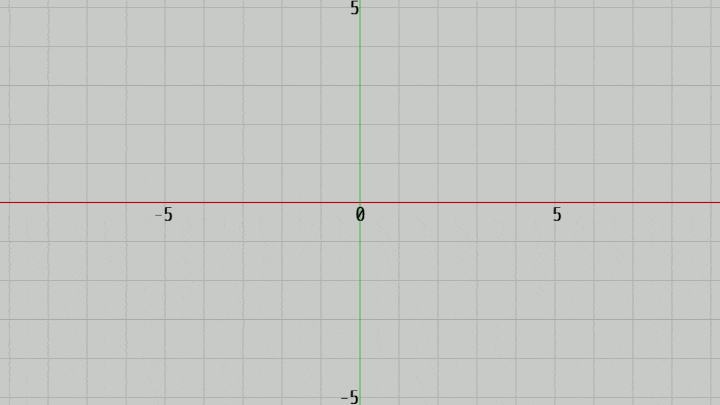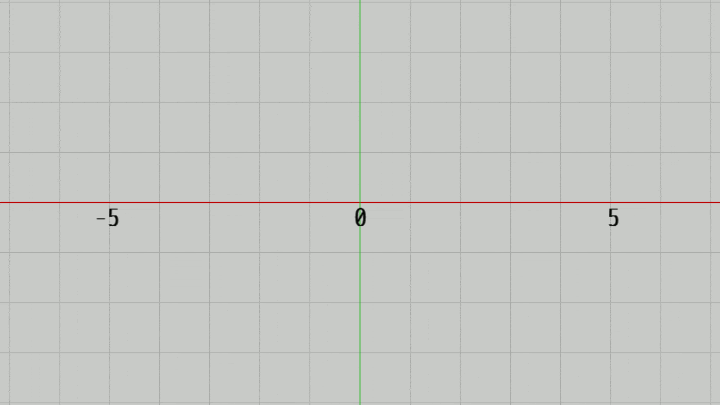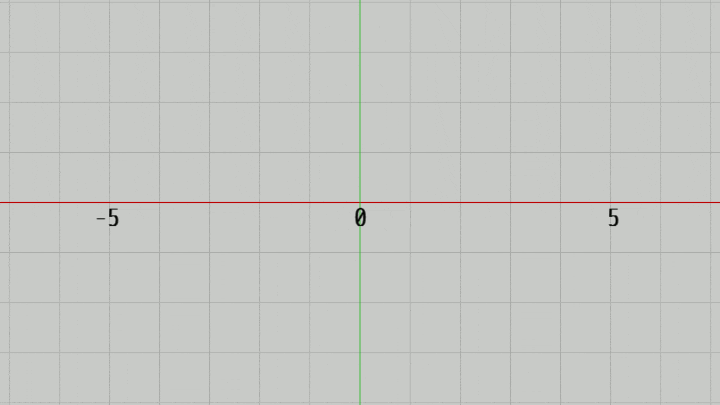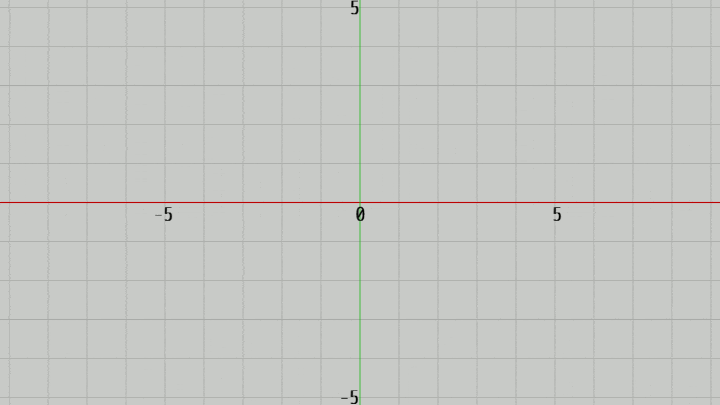
図5 図4のカメラからの撮影結果
このようにカメラの位置と実行結果の画面の表示範囲には密接な関係があるわけである。
もちろん具体的な表示範囲、すなわちカメラはXY平面上のどこからどこまでを撮影範囲とするのかを計算することもできるが、その際に必要となるのが上記のアスペクト比及びFOVである。
アスペクト比 (aspect ratio)とはここでは(実行結果の)画面の縦横比のことであり、具体的には「(画面の)横の長さ : 縦の長さ」のことである。したがって、本節冒頭で指定したアスペクト比 $16 : 9$ とは画面の 横 : 縦 が $16 : 9$ であることを意味する (図6)。
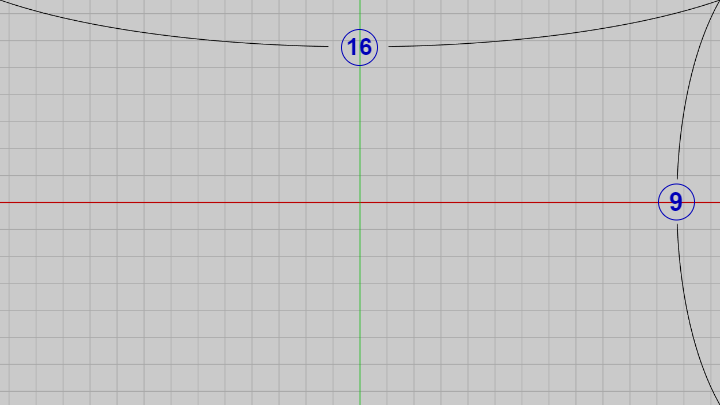
図6 アスペクト比 16 : 9
FOV (画角、Field of View)とはカメラの撮影範囲を角度で表したものである。FOVは角度を水平方向に測るのか、あるいは垂直方向に測るのかで分かれるが、以下では垂直方向のFOV(vertical FOV)の場合で説明する (Unityのデフォルトではvertical FOVであるため、この講義においてもFOVといえばvertical FOVを指すものとする)。
そして本節冒頭にもあるように以下ではFOVを $60^\circ$ として進める。
ここでXY平面上の原点を $O$、カメラの位置を $E$ とする。上の取り決めによってしばらくはカメラの位置は x座標、y座標ともに $0$ であるから、$E$ は z軸上にある。また y軸プラス側に点 $A$ を置き、y軸マイナス側に $|OA| = |OB|$ となるように点 $B$ を置く (図7)。そしてここではこの2点 $A$、$B$ を、画面に表示される y軸上の上端の点、下端の点とする (下図9)
このとき三角形 $EAB$ は二等辺三角形であり、辺 $EO$ はこの二等辺三角形を二等分する ($|OA| = |OB|$ であるため、点 $A$、$B$ の y座標を $A.\!y$、$B.\!y$ とすれば $B.\!y = -A.\!y$ である)。
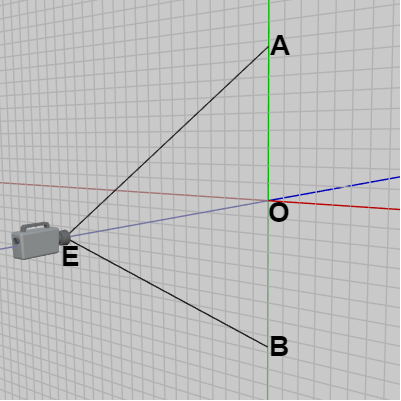
図7 Oは原点、A、B は y軸上の点でその長さは |OA|=|OB| (三角形 EAB は二等辺三角形) 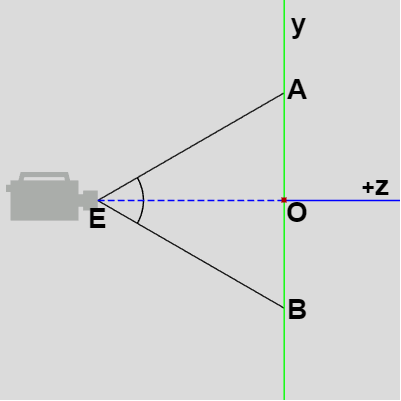
図8 FOVは図中の ∠AEB
図7の状況を真横から見たときのものが図8であるが、このときの $\angle{AEB}$ のことを FOV という (Field of View ; 垂直方向のFOVであるため詳しくは vertical FOV という)。したがって、例えばFOVが $60^\circ$ であるとは上図における $\angle{AEB}$ が $60^\circ$ であることを意味する。
そして上で定めたように、このときの実行結果の画面に表示される y軸の範囲は $B$ から $A$ までであり、$B$ より下、及び $A$ より上は画面には表示されない (図9)。すなわち、FOVとはカメラの撮影範囲(画面に表示される範囲)を表す角度を意味するわけである。
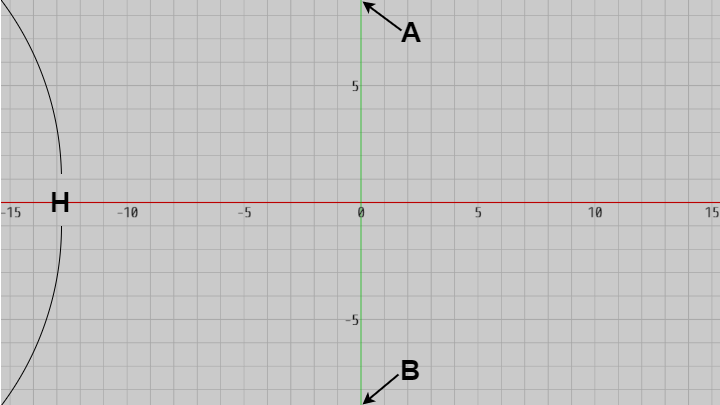
図9 画面上端 A、画面下端 B (画面の縦の長さは H)
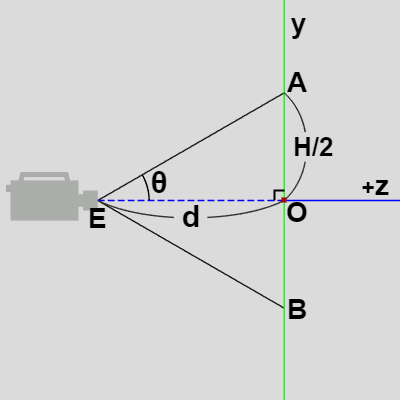
図10 ここで画面の縦方向の長さ(XY平面上で測った長さ)を $H$ とすれば、辺 $OA$ は画面の縦半分の長さであるから、その長さは $|OA| = H/2$ である。
原点 $O$ からカメラの位置 $E$ までの距離を $d$ とし、FOV ($\angle{AEB}$)の半分の角度を $\theta\ (\angle{AEO})$ とする (図10)。右図に示されるように三角形 $AEO$ は直角三角形であるから、\[d\tan{\theta} = H/2\ (=|OA|)\]である。
そして、画面のアスペクト比が $16:9$ であったから、画面の横の長さを $W$ とすれば $W/H = 16/9$ である。したがって、画面の縦の長さ $H$ がわかれば、横の長さ $W$ は\[ W = H \times (16 / 9) \]として求めることができるわけである。
プログラムを以下に示す。
[Code1] (実行結果 図11)
上図10において角度 $\theta$ はFOVの半分であり、XY平面からカメラまでの距離を $d$ とすれば、画面の縦半分の長さ $H/2$ は\[ d\tan{\theta} = H/2\]として求められるのであった。
そしてここでは画面の縦半分の長さが $9$ としてあらかじめ指定されているので、これを $H/2$ として上記の式から距離 $d$ が求められるわけである ( $d = (H/2)/\tan{\theta}$ )。
プログラム6行目の tanT は $\tan{\theta}$ のことであり、FOV * 0.5 は角度 $\theta$ のことである。
XY平面から $d$ だけ離れた位置にカメラを配置すれば、実行結果の画面において縦半分の長さが $9\ (= H/2)$ となり、(アスペクト比が $16 : 9$ であるから)横半分の長さは自動的に $16$ となる (図11)。
図11 Code1 実行結果 (縦半分の長さ 9、横半分の長さ 16)
(注 : 前節でも述べたが、プログラムではカメラを表すインスタンス変数 MainCamera への代入処理を省略している。しかし開始時点においてあらかじめ以下の処理が裏側で行われている。
)
プログラムは先程と同様である。
[Code2] (実行結果 図12)
今回は横半分の長さを $W/2$ とするとき、アスペクト比が $16:9$ であるから縦半分の長さ $H/2$ は\[ (W/2) \div (16/9) = H/2 \]として求められる (プログラム 3~5行目)。縦半分の長さがわかれば、あとはCode1と同様に進めればよい (7行目以降はCode1と同じ)。
なお、アスペクト比を $16:9$ に設定しているからといって実際の画面の横の長さと縦の長さの比が正確に $16:9$ になっているとは限らないことに注意しなければならない ($16:9$ に非常に近い値ではある)。より正確なアスペクト比を求めるには実行画面の横の長さ、縦の長さを表すint型定数 Screen.width、Screen.height (単位はピクセル)を取得して、この2つの長さから計算する必要がある。
例えば上記の3行目ではとして、aspect を計算しているが、この右辺を 16.0f / 9.0f としてしまうと実行結果において誤差が生じることがある。
図12 Code2 実行結果 (横半分の長さ 12)
Triangleは直角二等辺三角形であり、初期状態においては頂点の1つは原点に位置し、残り2つの頂点の位置は $(1,\ 0)$、$(0,\ 1)$ である。
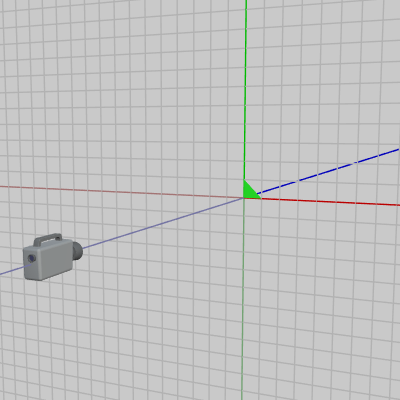
図13 カメラが適当な位置に置かれている 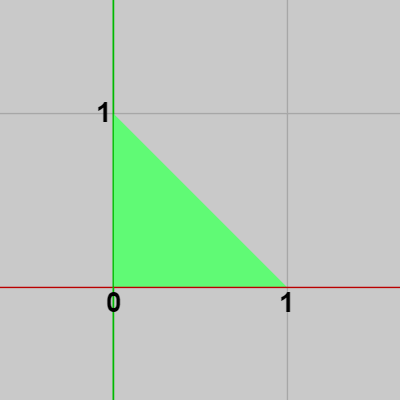
図14 Triangle 初期状態 (直角二等辺三角形)
Triangleを拡大せずにそのまま実行すると以下のように表示される (大きさは $1 \times 1$ のまま)。
図15
プログラムは以下のとおり。
[Code3] (実行結果 図16)
今回はカメラの位置があらかじめわかっている場合であり、したがってXY平面からカメラまでの距離 $d$ はカメラの位置から求めることができる。すなわち、カメラの z座標がそのままXY平面からカメラまでの距離となる。ただしカメラは z軸マイナス側に置かれているので、z座標はマイナスである。そのため距離 $d$ はその z座標の符号を反転した値、すなわち $d = -E.\!z$ である (4行目)。
距離 $d$ がわかればあとはFOVや $\tan{\theta}$、アスペクト比を使って今までのプログラムと同様に画面の縦半分の長さ、横半分の長さを求め、それらの長さをTriangleのスケール倍率とすればよい (12行目)。
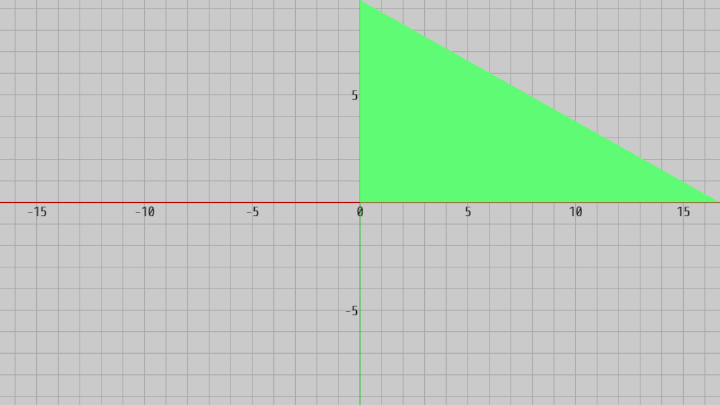
図16 Code3 実行結果 (Triangleの上の頂点が画面上端に、右の頂点が画面右端に来る)
本節及び次節では「スクリーン座標」や「ワールド座標」及び「ワールド座標系」という用語が使われる。スクリーン座標とはいわゆるピクセルを単位とする画面座標のことである。ワールド座標とは本節と次節においてはXY座標(XY平面上の座標)のことであり、本節及び次節においてワールド座標とあれば単にXY座標の代わりにワールド座標という語を使用しているに過ぎない。同様にここではワールド座標系とはXY平面のことであり、ワールド座標系という語は単にXY平面の代わりに使われているに過ぎない。
また、スクリーン座標は単位がピクセルなので画面上の長さや領域を表す際には $200$ pix、$400 \times 300$ pix のように表記する。
ワールド座標の場合特に決まった単位があるわけではないので、ここでは便宜上「wld」という単位を使用する。すなわち、XY平面上の長さや領域を $12$ wld、$4.8 \times 3.6$ wld のように表記する。
なお、Unityにおいてはスクリーン座標は左下隅が起点である。すなわち、画面左下隅のスクリーン座標が $(0,\ 0)$ である。
(注 : 今までの解説やプログラムではカメラの位置は z軸上、すなわち x座標、y座標はいずれも $0$ であり、したがって画面の中心には必ず原点が来ていたが、ここからはそのような制約はないので画面中心に必ずしも原点が来るとは限らない。例えば下の例では原点の位置は画面中心よりもやや右上である)
今、画面上のスクリーン座標 $M'$ の位置に大きさ $rw \times rh$ pix の長方形を置いたとする (図17)。$M'$ は画面左下隅から右に $mx$、上に $my$ 離れた位置の点である。画面中心のスクリーン座標を $P'(cx,\ cy)$ とし、$P'$ から $M'$ までの横方向の長さを $dx$、縦方向の長さを $dy$ とする。また、画面の横半分の長さを $w/2$、縦半分の長さを $h/2$ とする (以上すべて画面上のスクリーン座標、及びスクリーン座標系で測った長さであり単位は pix である。左下隅が起点 $(0,\ 0)$ )。
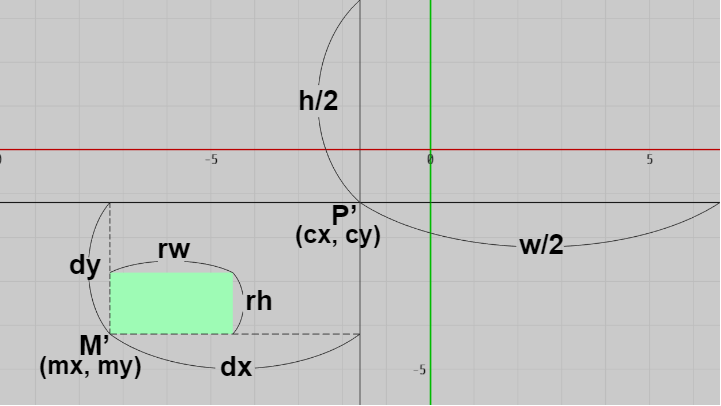
図17 画面上のスクリーン座標、及び画面上の長さ (単位 pix)
上記のスクリーン座標 $M'$ に対応するワールド座標を $M$ とし、スクリーン座標 $P'$ に対応するワールド座標を $P$ とする。また、上図において $w/2$、$h/2$、$rw$、$rh$、$dx$、$dy$ はすべてスクリーン座標系での長さであるが、これらをワールド座標系での長さに変換したものをそれぞれ $W/2$、$H/2$、$RW$、$RH$、$s$、$t$ で表す (図18 ; 以上はすべてワールド座標、及びワールド座標系で測った長さであり単位は wld である)。
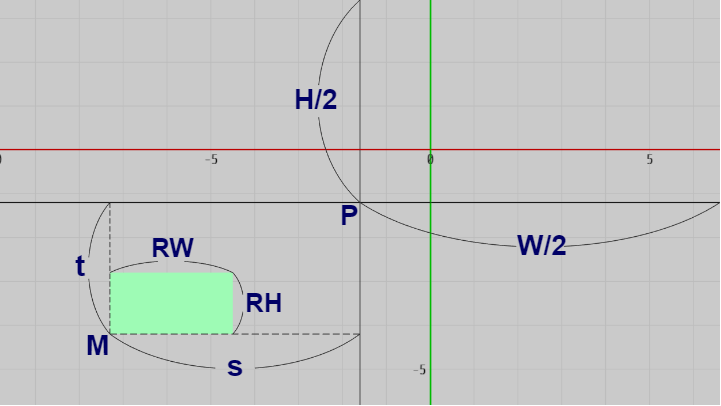
図18 P や M はワールド座標、RW、RH、s、t などはワールド座標系での長さ (単位 wld)
カメラの位置があらかじめ決められているものとすれば、XY平面からカメラまでの距離 $d$ はCode3で述べたようにカメラの z座標から求めることができ、$d = -E.\!z$ である。XY平面からカメラまでの距離 $d$ がわかればFOVの半分の角度を $\theta$ とするとき、画面に表示されているXY平面上の縦半分の長さ $H/2$ は、前半の解説にあるように\[d\tan{\theta} = H/2\]である (単位は wld)。
XY平面上の縦半分の長さ $H/2$ は、画面上においては $h/2$ に相当するわけである。すなわち、$H/2$ wld が $h/2$ pix に相当するということであるが、このことから画面上の $1$ pix はXY平面上では何 wld に相当するかを計算できる。つまり、以下の計算を行えばよい。
\[ (H/2)/(h/2) = H/h = WldPerPix \]ここに現れた変数 $WldPerPix$ は、画面上の $1$ pix がXY平面上において何 wld に相当するかを表す変数であり、スクリーン座標とワールド座標の変換において基本となるものである。
この $WldPerPix$ を使って、画面上の長さ $rw$、$rh$、$dx$、$dy$ をそれらに対応するワールド座標系での長さ $RW$、$RH$、$s$、$t$ に変換するには以下の計算を行うだけである。
\begin{align*}&rw \cdot WldPerPix = RW \\ \\&rh \cdot WldPerPix = RH \\ \\&dx \cdot WldPerPix = s \\ \\&dy \cdot WldPerPix = t \\ \\\end{align*}画面の中心を表すスクリーン座標 $P'$ に対応するワールド座標 $P$ はカメラの座標からすぐに求められる (前節 Code7)。すなわちカメラの位置を $E$ とすれば $P = (E.\!x,\ E.\!y)$ である。
上図18において長方形の左下隅の位置を表すワールド座標 $M$ は $P$ から x軸方向に $s$、y軸方向に $t$ だけ離れているから、結局 $M = (P\!.x + s,\ P\!.y + t)$ である (この例では $s, t < 0$ )。
下図19はここで使用する長方形 Rect の初期状態である。Rectは初期状態では1辺の長さが $1$ の正方形であり、左下隅の頂点が原点に位置している。また、今回のプログラムと次のCode5では画面右下に図20のような2組の数値が表示されるが、これはマウスカーソルの現在位置、すなわちマウスカーソルのスクリーン座標が表示されているのである。
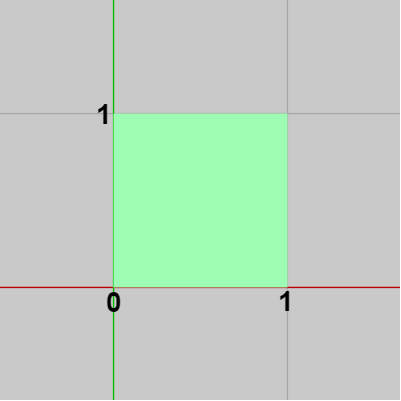
図19 Rect 初期状態 
図20 画面右下にマウスカーソルの現在位置が表示される
プログラムを以下に示す。
[Code4] (実行結果 図21)
上の解説をそのまま実装したものであり、使われている変数も上の解説と同じである。
なお今回のプログラムで注意すべき点は、実行結果の画面に表示されるグリッド線はXY平面上において $1$ ずつの間隔で並んでいるわけではないという点である。
今回表示されるグリッド線はスクリーン座標の起点(左下隅の起点)を基準にして $50$ pix 間隔で並んでいる。つまり、下図の縦のグリッド線は左端から右に向かって $50$ pix の間隔で並んでおり、横のグリッド線は下端から上に向かって $50$ pix の間隔で並んでいる。
これは、Rectが実際に $(200,\ 100)$ の位置に $250 \times 150$ pix の大きさで置かれているかどうかを確認しやすくするためである。

図21 Code4 実行結果 (グリッド線は左下隅を起点にして 50 pix 間隔で並んでいる)
(今回のプログラムも次のプログラムもオブジェクトの位置や大きさをスクリーン座標系で指定するものであるが、これはいわゆるベクターグラフィックスにおいて'力づくで'ラスターグラフィックスを実装しているだけである。そのため厳密ではなく、1 pix 程度の誤差は生じる)
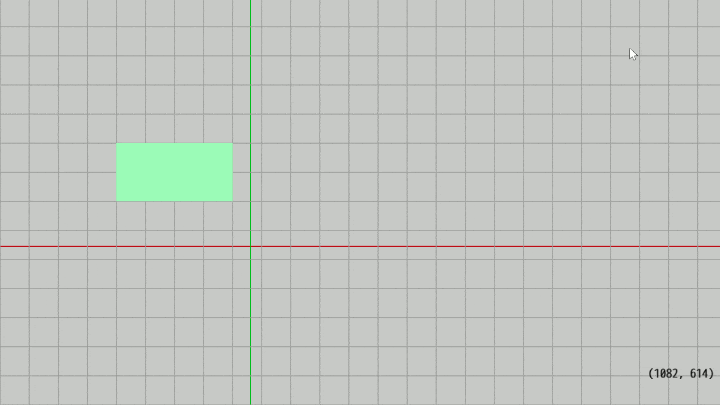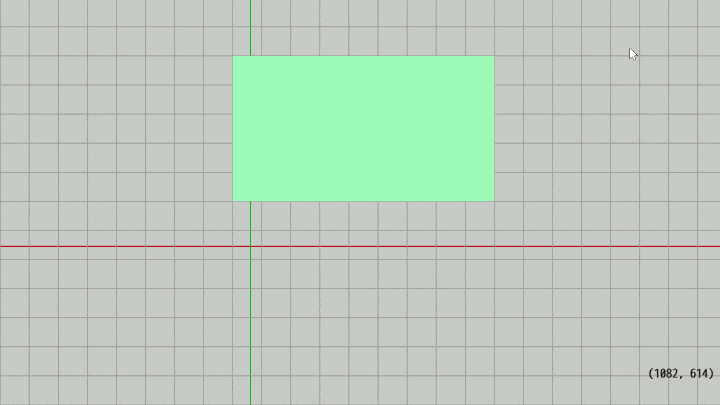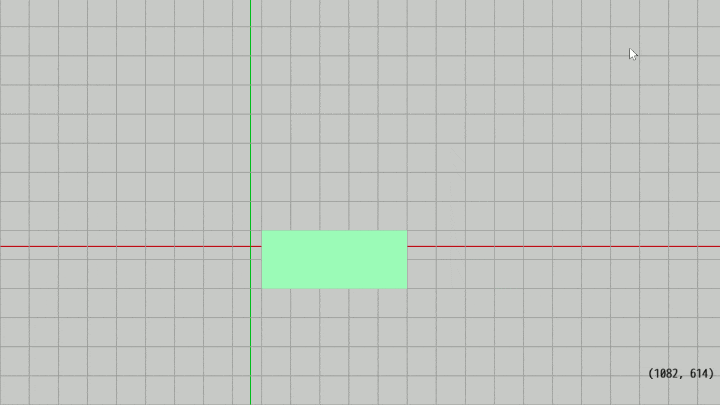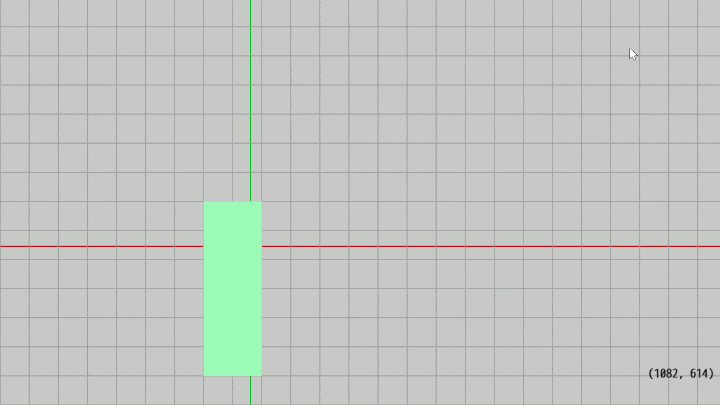
図22 Code5 実行結果 (画面上のグリッド線は左下隅を起点にして 50 pix 間隔で並んでいる)
キー操作は以下のとおり。
H、J、K、L : Rectの位置を上下左右に 50 pix ずつ動かす (H、L が横方向、J、K が縦方向の移動)
Shift + H、J、K、L : Rectの大きさを 50 pix ずつ変化させる (H、L が横方向の調整、J、K が縦方向の調整)
[Code5] (実行結果 図22)
今回はプログラム実行中にもスクリーン座標とワールド座標の変換を行うので、初期化ブロックではその処理の際に必要となる $cx$、$cy$ (画面中心を表すスクリーン座標)、$WldPerPix$ などをインスタンス変数にしている (10~14行目 ; 画面のサイズが変化したり、カメラが動くことはないのでこれらの変数の値はプログラム実行中常に同じである)。
16~19行目の i_locX、i_locY、i_width、i_height はRectの(左下隅の)位置、及びRectの大きさを表すためのインスタンス変数で、上図22のグリッド線において何マス目の位置か、あるいは何マス分の大きさかを表している。例えばここでは i_locX、i_locY はともに $1$ であるが、これは左下隅から右に $1$ マス、上に $1$ マス分離れた位置にRectが(Rectの左下隅)が置かれることを意味する。i_width、i_height はともに $2$ であるが、これは開始時点におけるRectの大きさが縦横ともに $2$ マス分であることを意味する。
これらのインスタンス変数の値をスクリーン座標系での値に変換するには、これらのインスタンス変数に $50$ を掛ければよい。すなわちプログラム開始時点においては、Rectの左下隅の位置は $(50,\ 50)$ であり、その大きさは $100 \times 100$ である。
26~45行目のキー操作ではShiftキーが押されて入れば i_width、i_height を変化させ(大きさの変化)、押されていなければ i_locX、i_locY を変化させる (位置の変化)。これらのインスタンス変数にはいずれも下限、上限があり、例えば i_locX、i_locY の下限は $0$ なのでRectの左下隅の位置を画面左下隅よりも左あるいは下に移動させることはできない。また、i_width、i_height の上限は $20$ なのでRectの縦横の長さを $1000$ pix よりも大きくすることはできない。
52行目以降の処理は先程のプログラムと同じである。
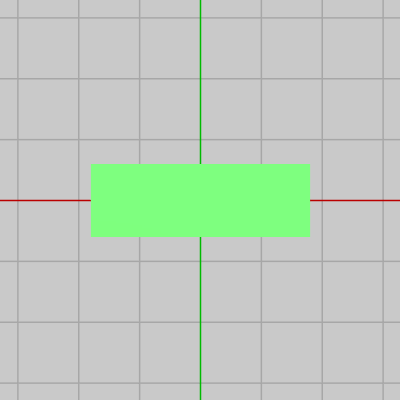
図23 Green 初期状態 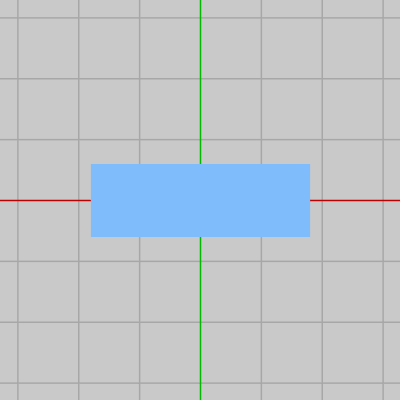
図24 Blue 初期状態
この2つの長方形をややずらして表示したときの結果が下図25であり、2つの長方形が重なっているが、ここではGreenが手前に表示されている。
このときのXY平面及びカメラを離れた位置から見たときのものが図26である。図に示されるようにカメラの位置は $(0,\ 0, -10)$ であるから、XY平面からカメラまでの距離は $10$ である。
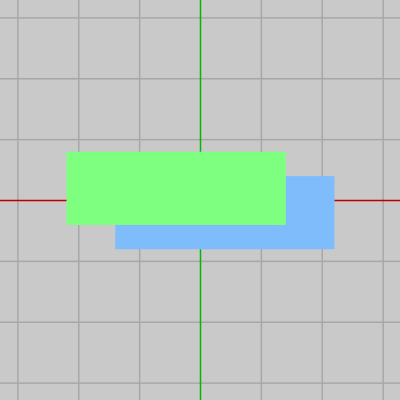
図25 2つの長方形を表示 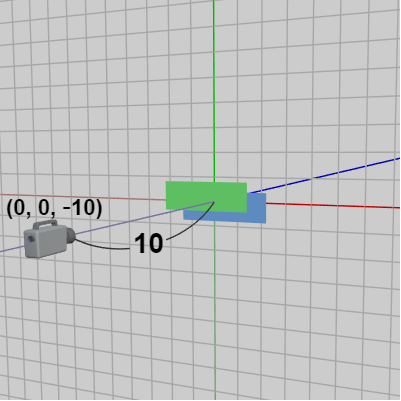
図26 カメラの位置はXY平面から 10 だけ離れている
上図25の場合は2つの長方形はいずれもXY平面上に置かれているのでその z座標は $0$ である。したがって、カメラからの距離はいずれも $10$ である。上図の場合はたまたまGreenが表示されているが、オブジェクトが重なっている場合、カメラからの距離が近い方のオブジェクトが手前に表示される (これは設定によって変えることができるが、デフォルトではカメラからの距離が近い方が手前に表示される)。
上の状況ではいずれも z座標は $0$ であるが、例えばここでBlueの z座標を $-0.01$ にしたとしよう。この場合にはBlueはカメラに $0.01$ だけ近づいたわけである。このときの実行結果が下図27であるが、BlueはGreenよりも $0.01$ だけカメラに近い位置に置かれているので、確かにBlueが手前に表示されるようになる。
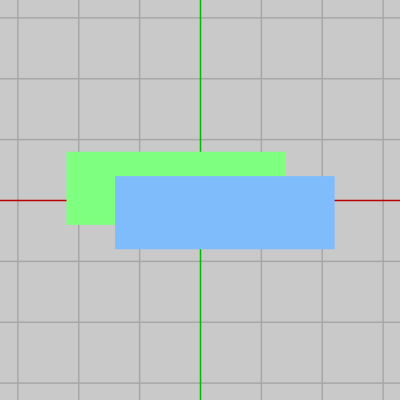
図27 z座標 Blue:-0.01 Green:0 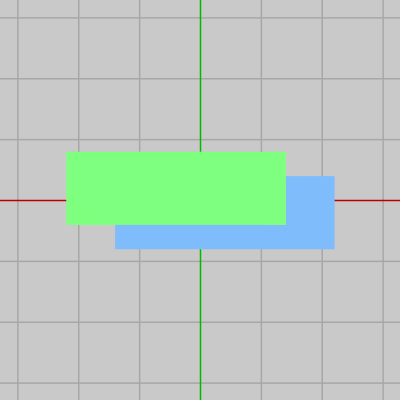
図28 z座標 Blue:-0.01 Green:-0.02
この状況からGreenの z座標を $-0.02$ にしたとしよう。この場合両者の z座標は Blue $-0.01$、Green $-0.02$ となるので、今度はGreenの方がカメラに近くなるわけである。図28はこのときの実行結果であるが、またGreenが手前に表示されるようになっている。
そしてここで重要なのが上図25、図27、図28では長方形の z座標を $0.01$ あるいは $0.02$ だけずらしているが、見た目ではその違いがわからないという点である。つまり、2Dオブジェクトを $z=0$ のXY平面上に置くのも、z座標を $0.01$ や $0.02$ だけずらして置くのも置かれる位置や大きさは結果的には変わらない、しかし、カメラにわずかでも近いオブジェクトの方が必ず手前に表示されるのである。
今述べたことはおそらくは自明なことであったろう。しかし、これから実装するミニマップや次節におけるテキストの表示などは今述べたことの応用に過ぎない。以下に展開する実装方法は、ミニマップやテキストの実装方法としては非常に簡単で応用のしやすいものである (ただし以下で解説する方法は2D空間限定の方法である)。
まずは前節のCode8で用いたサーキットの例を用いて進める。前節でも触れたが、ここで使うサーキット(下図29)はそのサイズが大きいため、今回のプログラムではサーキットが画面全体に収まるようにするために、カメラをXY平面からやや離して置いている。
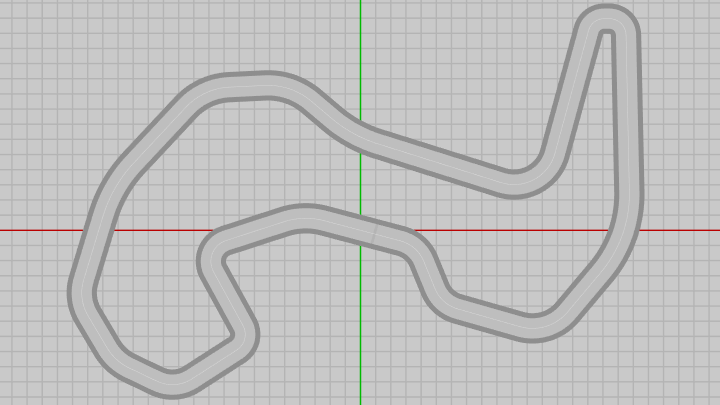
図29 XY平面上に置かれたサーキット
ここでもサーキット上を走行するオブジェクトとして以下の Vehicle を使用する (図30)。またミニマップ上でVehicleの位置を表すオブジェクトとして右図の Dot を使用する (下図のグリッド線の間隔は適当であり、その間隔は必ずしも $1$ ではない)。
図30 Vehicle 初期状態 
図31 Dot 初期状態
さらにミニマップ用のサーキットとして、上記のサーキットと全く同じ形状のものを用意する。ただし下図に示されるように形は同じであり、全体の大きさも同じではあるが、路面の幅などは狭くなっている。
以下このミニマップ用に使われるサーキットを単に MiniMap と呼ぶことにする。またMiniMapの中心部分に黄色い点があるが、この黄色い点はMiniMapの初期状態では原点に位置している。MiniMapの初期状態において原点に置かれているこの黄色い点をここでは「オブジェクト原点」と呼ぶことにする。

図32 MiniMap 初期状態 (ミニマップ用のサーキット ; 原点の黄色い点がMiniMapのオブジェクト原点)
以下のプログラムは前節のCode8を多少変更して、上記のMiniMap及びDotの運動を追加したものである。
[Beta6] (実行結果 図33)
27行目までは前節のCode8と同様の処理である。前節のCode8では J、K キーによってVehicleを進めたり、戻したりすることができたが、今回は常にVehicleはサーキット上を走り続けるように変更されている。このVehicleの移動も S キーによって移動、停止の切り替えが行えるようになっている。
29~30行目が追加部分である。追加した処理の内容は、Dotの位置を毎フレーム Vehicleと同じ位置に移動させ、MiniMapを初期状態のまま配置ているだけである。ただしプログラムにあるように、Vehicle及び Dot、MiniMap の z座標はいずれも $-0.01$ となっており、これによってXY平面上に置かれたサーキット($z = 0$)よりも手前に表示されるようになる。
Dotは毎フレーム Vehicleと同じ位置に移動することになるので、下図に示されるようにDotは常にVehicleと一体となって移動することになる (見やすさのためにDotの位置はわずかにずらし、Dotを赤、MiniMapを水色を変えている。実際にはVehicleとDotは完全に重なってしまう)。
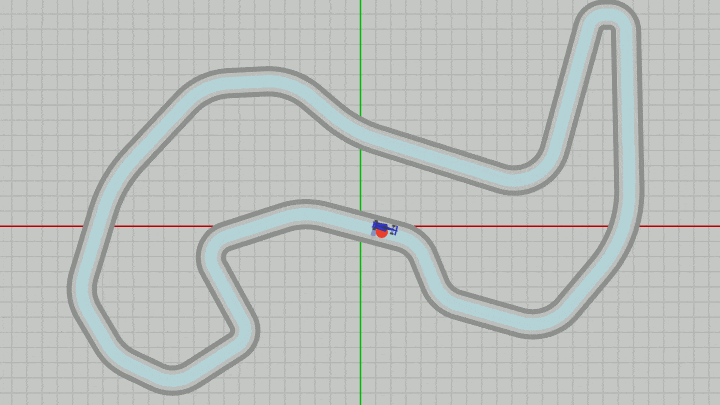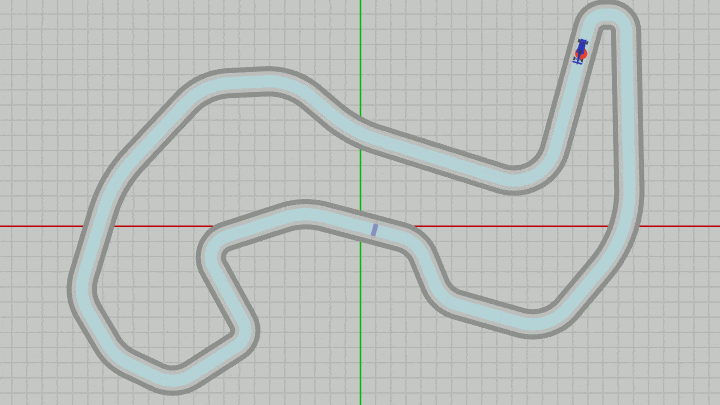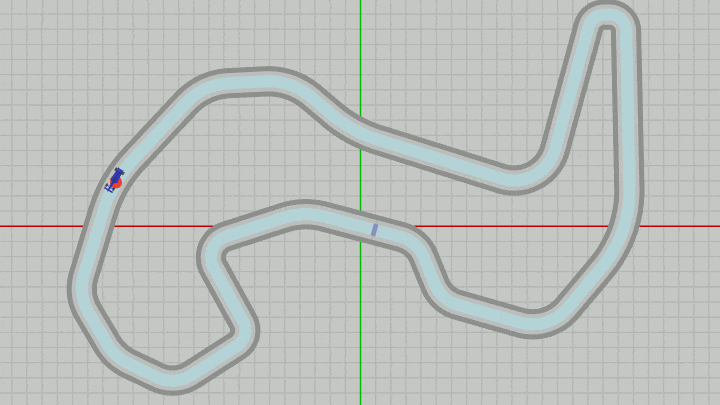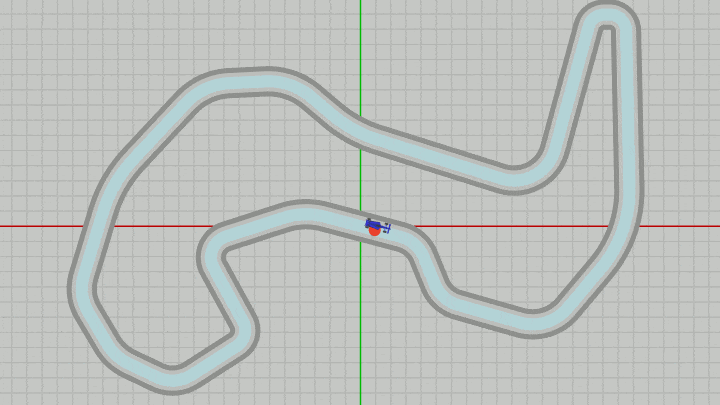
図33 Beta6 実行結果 (Vehicle、Dot、MiniMapはいずれも z=-0.01 なのでサーキットよりも手前に表示されるようになる)
ここからMiniMap及びDotに対していくつかの変換を行うが、ここからの一連の流れは重要である。
上のBeta6では本来のサーキットとミニマップ用のサーキット(MiniMap)が同じ位置に置かれており、さらにVehicleとDotも常に同じ位置にあるためこれらのオブジェクトは常に重なっていた。例えば上記のプログラムにおいてMiniMap及びDotの位置を毎フレーム x軸方向に $-5$ だけずらすと、すなわち29行目以降を以下のように変更すると、
MiniMapとDotは以下の実行結果に示されるように上図33の場合と比較して x軸方向に $-5$ だけずれた位置に表示される。そして今回はDotの z座標が $-0.03$、MiniMapの z座標が $-0.02$ となっているので、画面の一番手前にはDotが表示され、VehicleとMiniMapが重なったときにはMiniMapが手前に表示されるようになる (Vehicleの z座標は $-0.01$)。
このときのMiniMapのオブジェクトの原点(黄色い点)の x座標、y座標は $(-5,\ 0)$ である。下図のグリッド線は $1.5$ 倍に拡大されているため、グリッド線の間隔は $1.5$ である ($1$ ではない)。
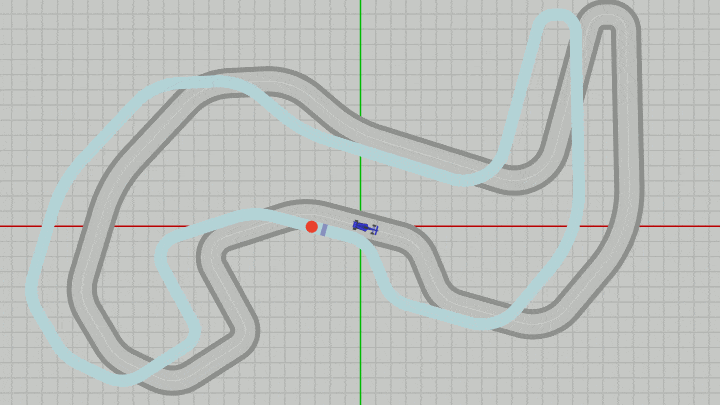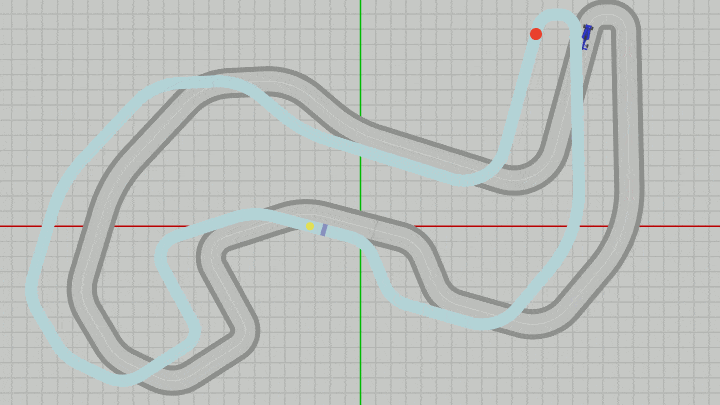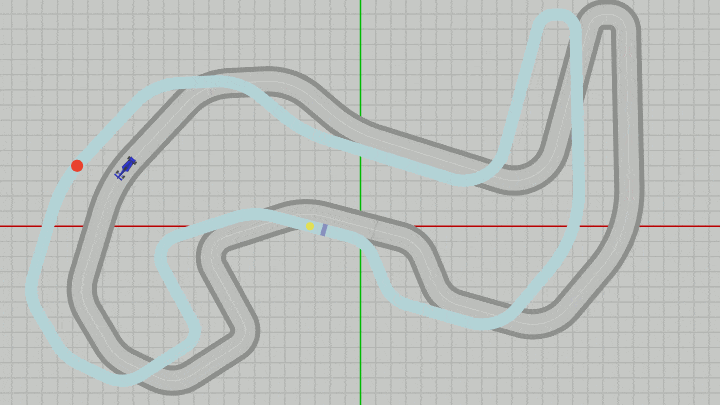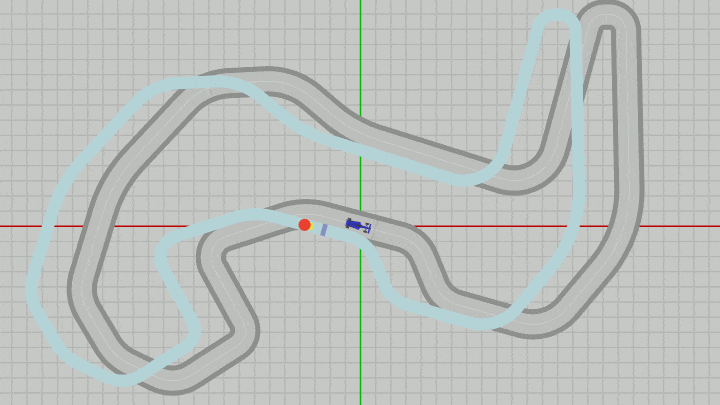
図34 Beta6からMiniMapとDotを x軸方向に -5 だけずらした場合 (グリッド線の間隔は 1.5 ; 各オブジェクトの z座標は手前に表示される順に、Dotが -0.03、MiniMapが -0.02、Vehicleが -0.01 である)
MiniMapがどこに置かれてもDotは常にMiniMap上を移動するので、この2つのオブジェクトには親子関係を設定する方が自然である。例えば上記では毎フレーム DotとMiniMapの両方に x軸方向の $-5$ の移動である mv が加算されているが、親子関係を設定すればこういった同じ加算を2つのオブジェクトに対してする必要がなくなる。
DotとMiniMapに親子関係を設定した場合において、両者を x軸方向に $-5$ だけずらして置く先程の処理は以下のように記述される (今回は親子関係が設定されているのでDot及びMiniMapの位置設定には position ではなく localPosition が使われている)。
この場合にはDotはMiniMapの子オブジェクトであるため、z座標 $-0.01$ はMiniMapの z座標よりも $0.01$ マイナス側にあることを意味し、実際のDotの z座標は $-0.03$ である。そしてこのコードでは x軸方向の $-5$ の移動はMiniMapだけに行われるようになっているが、もちろん実行結果は先程と同じである (図34)。
さらにこの状態からMiniMap及びDotの大きさを半分にする。両者には親子関係が設定されているので、このスケールも親オブジェクトであるMiniMapに対してのみ実行すればよい。具体的には以下のとおり。
先程のコードからはMiniMapに対して $0.5$ 倍のスケールが追加されているだけである。
この変更後の実行結果が以下の図35である。MiniMapとDotの大きさが縮小されているが、これは上図34の状態からMiniMapのオブジェクト原点のある $(-5,\ 0)$ を中心に $0.5$ 倍縮小した結果である (スケールは必ずオブジェクト原点を中心に行われる)。
なお下図の実行結果においてもグリッド線の間隔は $1.5$ である。
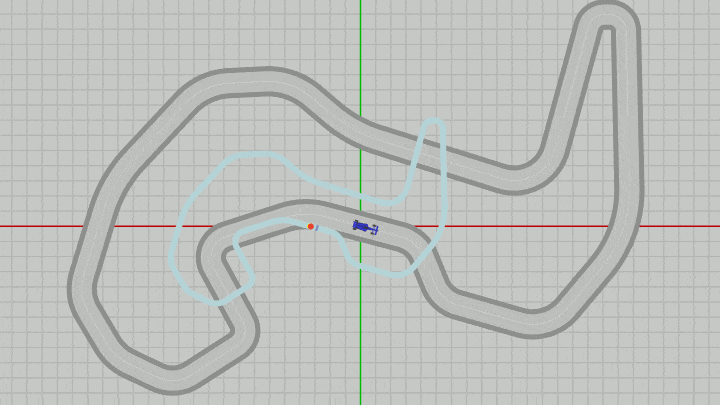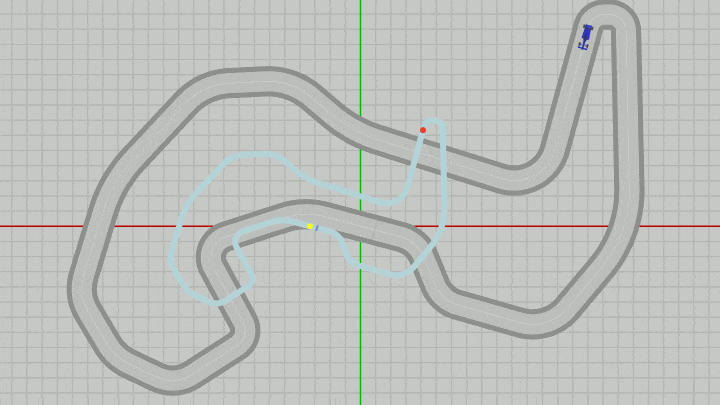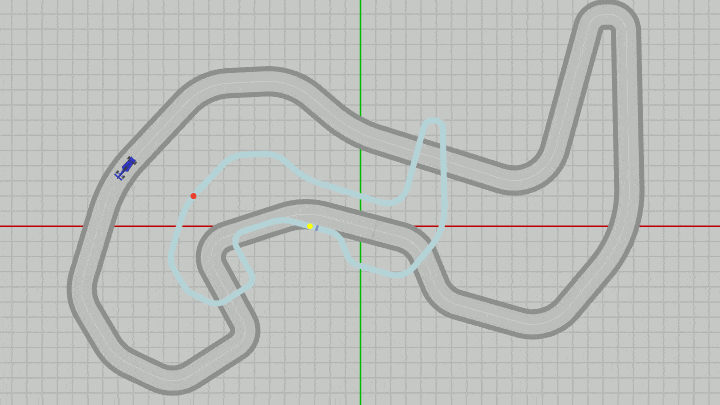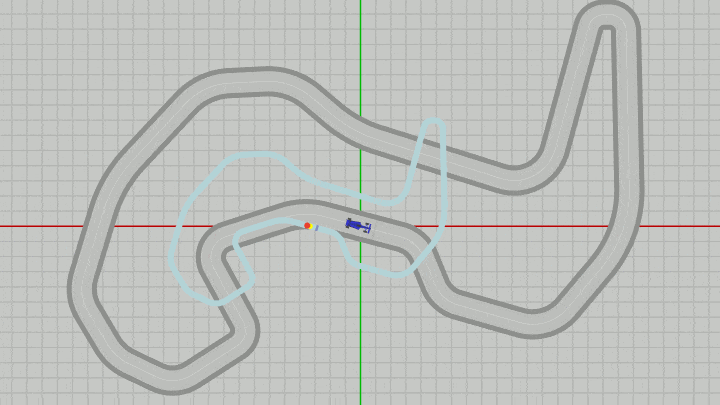
図35 上図34の状態からMiniMapのオブジェクト原点を中心にMiniMapとDotの大きさを 0.5 倍にした状態 (グリッド線の間隔は 1.5)
次のプログラムは今までに述べてきたことをまとめたものである。
サーキット上を一定の速度でVehicleが走行している。Vehicleの現在位置を表示するためのMiniMapがXY平面から $0.02$ だけずらして置かれており ($z=-0.02$)、その子オブジェクトとしてDotがMiniMapから z軸方向マイナス側に $0.01$ だけずらして置かれている ($z=-0.03$)。そして両者には $0.5$ 倍のスケールが実行されている。
さらにここでは、以下のキー操作によってMiniMapを上下左右に移動させる。
H : MiniMapを左に動かす
L : MiniMapを右に動かす
J : MiniMapを下に動かす
K : MiniMapを上に動かす
プログラムは以下のとおり。
[Code6] (実行結果 図36)
初期化ブロックの8行目ではDotとMiniMapの親子関係を設定している。このプログラムではMiniMapは $0.5$ 倍にスケールされるが、プログラム実行中においてはその倍率に変化はないのでその処理は初期化ブロックで行われる (11行目)。また今回は開始時点においてMiniMapのオブジェクト原点の位置は $(0,\ 0)$ に置かれた状態から始まる。そして上で見てきたようにMiniMapはVehicleやサーキットよりも手前に表示するために z座標を $-0.02$ としている (10行目。Vehicleの z座標は $-0.01$、サーキットの z座標は $0$)。
上記ではいくつかのコードによってMiniMap(及びDot)の位置や大きさを変えてきたが、このプログラムにおいては35行目以降がその処理に該当する。Dotに対する変換内容(Vehicleと同じ位置に移動させ、その z座標を $-0.01$ にする処理)は変わらないが、それ以降の部分でキー操作によってMiniMapを動かす処理を入れている。
指定のキーがおされている間は x軸方向、y軸方向に $0.05$ ずつ移動するが、このときに変化するのはMiniMapの x座標、y座標のみであり、z座標は初期化ブロックで設定した値 $-0.02$ のままである。毎フレーム 37行目でMiniMapの現在位置 mp を取得し、この mp の x座標、y座標に移動分を加算している。つまり、変更されるのは x座標、y座標のみなので z座標の値は常に変わることはない (37行目の mp の型をVector2にしてもエラーにはならないが、Vector2にしてしまうと55行目で再度MiniMapにこの変数をセットした際に z座標の情報が失われてしまうので注意が必要である)。
このプログラムで目的としていることは、MiniMapを適当な大きさに変更しプログラム実行中にどのように移動させても、サーキット上を走行するVehicleの現在位置がMiniMap上にDotとして表示され、さらにMiniMapが常に画面の手前に表示されるようにするという点である。
下図の実行結果に示されるようにMiniMapを適当な大きさに変更し、適当な位置に移動させても、サーキット上のVehicleの現在位置がMiniMap上には常に表示され、どの位置においてもMiniMapは画面の一番手前に来る。そして重要なことは各オブジェクトが重なったときの前後関係(どれが手前に表示されるか)の決定は z座標をわずかにずらすという形で行われているのである。
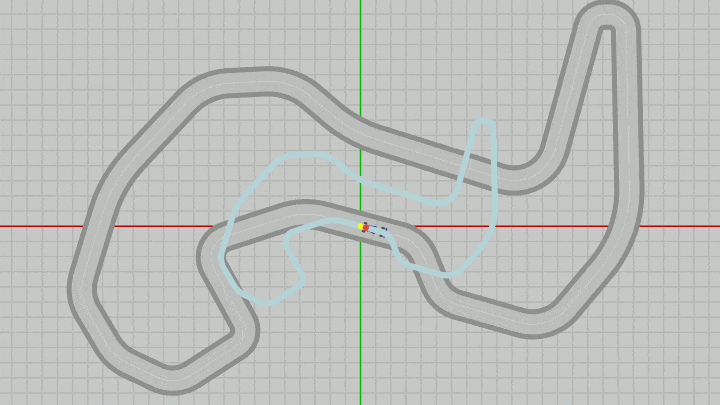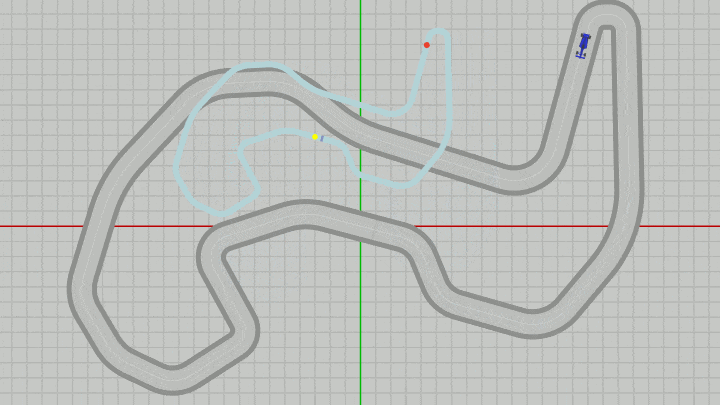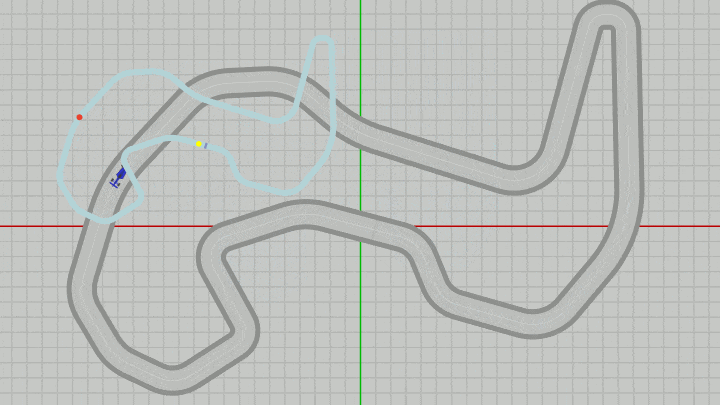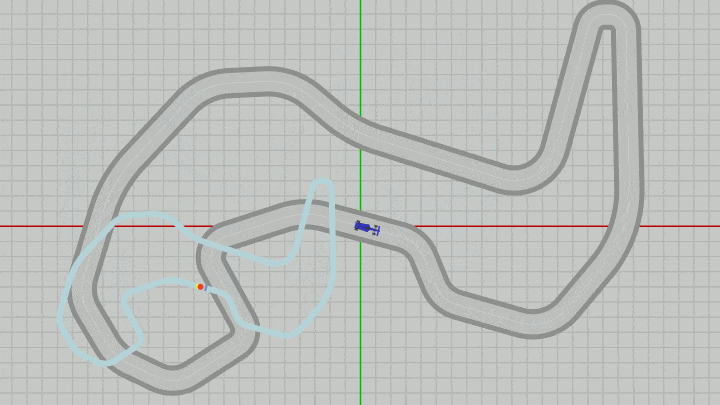
図36 Code6 実行結果
また、今回の実装において毎フレーム のVehicle及びDotに対する平行移動の内容は同じである (32~35行目 ; ともに x座標、y座標が pos.x、pos.y で、z座標は $-0.01$ )。平行移動の内容が同じなのは、サーキット上におけるVehicleの現在位置をMiniMap上に表示するという目的のためである。
平行移動の内容は同じであるが、VehicleとDotは同じ位置に置かれるわけではない (つまり両者が重なって表示されたりはしない)。それはDotがMiniMapの子オブジェクトであり、MiniMapに対する変換の影響を受けるためである。
もし読者がこのあたりの理解があいまいなのであれば、再度MiniMapが何の変換も受けていないBeta6に戻って考えるとよい。Beta6ではMiniMapは初期状態であり、初期状態においてはMiniMapはサーキットと形、大きさが同じであった。その状況ではVehicleと同じ位置に毎フレーム Dotを移動させると(平行移動の内容を同じにすると)、VehicleとDotの位置は常に同じになるため、両者は重なって表示されたのであった (図33)。
重要なのはそこからの一連の手続きである。そこからいろいろな'細工'をすることによって、上図36のようなMiniMapを実現しているわけである。そしてその根底にあるのがオブジェクトの親子関係と z座標のずらしなのである。
なお1点補足しておこう。
上のプログラムではMiniMapの位置の変更は行われるが、大きさは常に同じであり変化しない。もし、MiniMapの大きさをスケールによって変化させる場合、MiniMapの拡大縮小はMiniMapのオブジェクト原点を中心にして行われる (これは他のオブジェクトでも同じである)。実際、下図はMiniMapをある位置から動かさずに、その大きさだけを変化させているときの様子であるが、オブジェクト原点(黄色い点)を中心に拡大縮小が行われていることがわかるであろう。
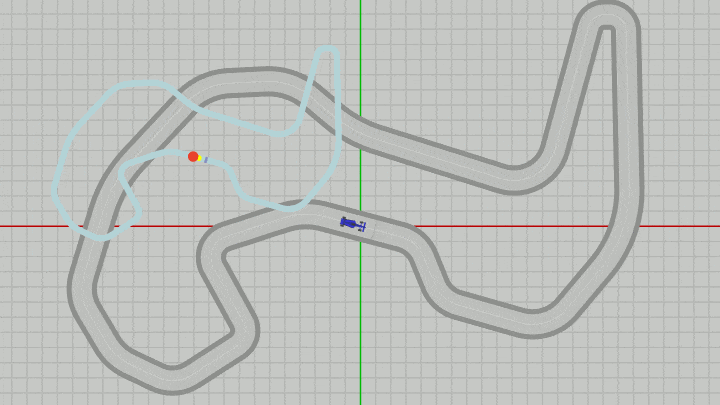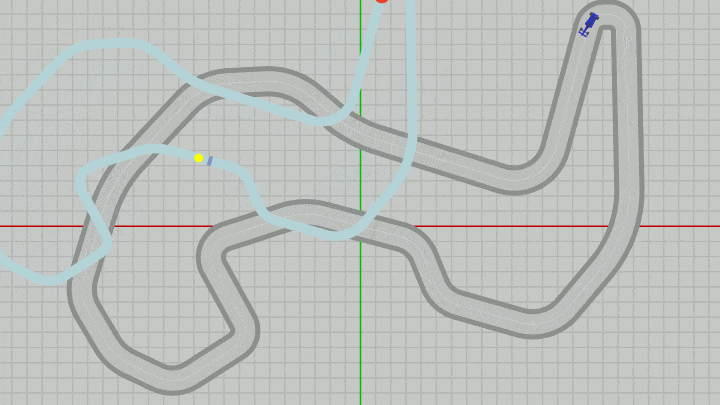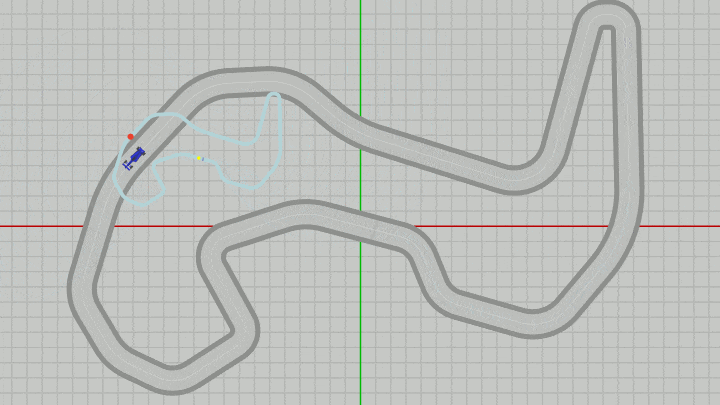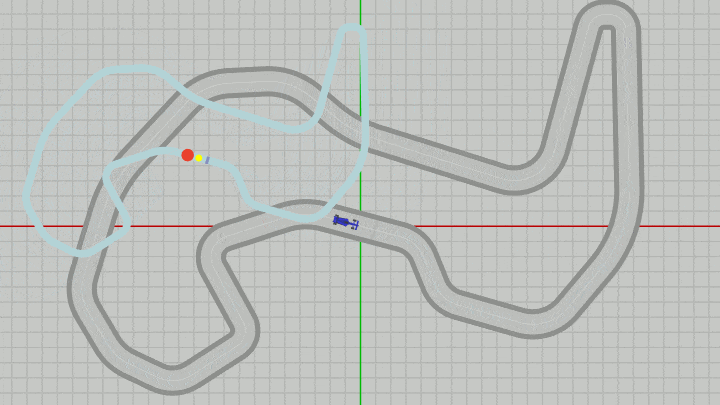
図37 MiniMapに対してスケールを実行しているときの様子(オブジェクト原点を中心にスケールは行われる)
一番簡単な方法はUnityのInspectorを使う方法であり、以下その方法で進める。
上でも触れたが、上記のCode6ではサーキット全体が画面に収まるようにカメラはやや離れた位置に置かれていた。今回はカメラの位置をレース用の位置に戻すが、その位置はXY平面から $7.2$ だけ離れている。つまり サーキット上をVehicleが走行する間は、カメラはXY平面から $7.2$ だけ離れた位置でVehicleの追跡を行う (常にカメラの z座標は $-7.2$)。
MiniMapの位置及び大きさを決定するために、まずカメラをXY平面から $7.2$ だけ離れた位置に配置する。その際カメラの x座標、y座標はどこでもよいが、ここでは簡単のためともに $0$、すなわち $(x,\ y,\ z) = (0,\ 0, -7.2)$ の位置にカメラを配置する。
このカメラ配置でプログラムを実行し、初期状態のMiniMapのみを表示すると実行結果の画面は下図のような表示になる (今回はカメラをXY平面に近づけているので初期状態のMiniMapはその一部しか画面に入らない)。
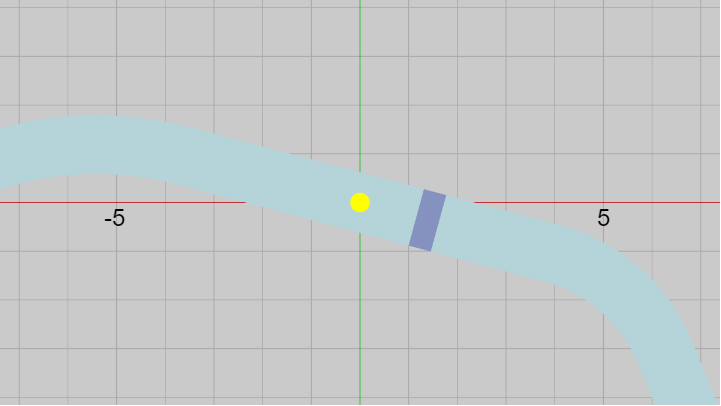
図38 MiniMap 初期状態 (カメラの位置は (0, 0, -7.2) で、比較的XY平面に近い位置に置かれているので実行結果の画面にはMiniMapの一部しか表示されない)
ここからMiniMapの位置及び大きさの調整を始める。
Unity画面上において Hierarchy Window 内にある「MiniMap_Cr」を選択する (図39)。選択すると Inspector 内にMiniMapに関する情報が表示されるが、このInspector内の Transform という項目にある「Position」「Scale」の各値をここでは変更する (図40)。
Scale はMiniMapの大きさを調整するためのものであり、今回はMiniMapを $0.07$ 倍に縮小するので、x 及び y に $0.07$ を入力する。Position はMiniMapの位置を調整するためのものであるが、今回は画面左上にMiniMapを表示するので x に $-5$、y に $1.6$ を、さらに常に画面手前に表示されるように z に $-0.02$ を入力する。これによってMiniMapのオブジェクト原点(黄色い点)が $(-5,\ 1.6, -0.02)$ の位置にくる。
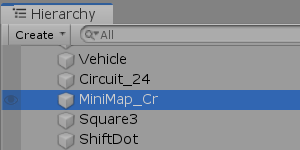
図39 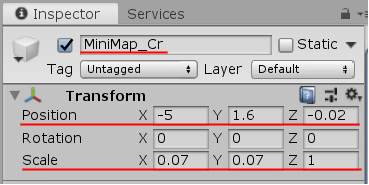
図40
この調整によってMiniMapは以下のように表示されるが、これをMiniMapの正式な位置、大きさとし、今回のプログラムでは実行中 常にMiniMapが下図の状態で画面上に表示されるようにする。
常に画面上の指定の位置に指定の大きさでMiniMapが表示されるようにするためには、さらにもう1つだけ準備が必要になる。
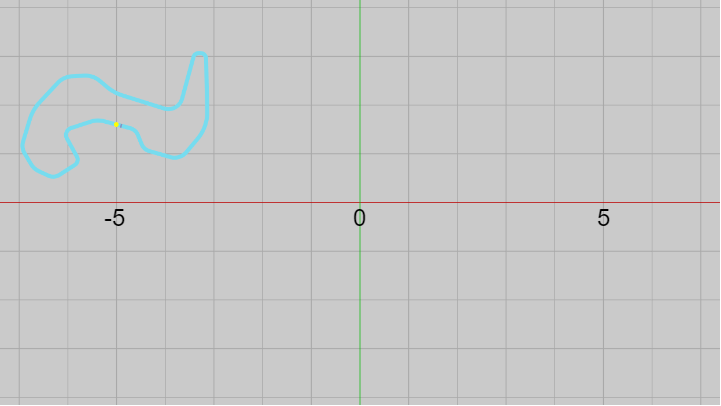
図41 MiniMap上の黄色い点がオブジェクト原点の位置で、その座標は (-5, 1.6, -0.02)
上図41の状況を離れた位置から見たときのものが下図42である。図中の $E$ はカメラの位置であり、ここでは $E = (0,\ 0, -7.2)$ である。$F$ はMiniMapのオブジェクト原点であり、先程定めたように $F = (-5,\ 1.6, -0.02)$ である (MiniMapには z座標の'ずらし'が行われている)。
また図中には緑色のベクトルがあるが、これは始点を $E$、終点を $F$ とするベクトルであり、以下このベクトルを $\boldsymbol{\mathsf{w}}$ で表す。
下図の状況を簡単にいうと、カメラの位置 $E$ からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを配置すれば、画面上では上図41のように表示されるということである (MiniMapにはスケールが行われているものとする)。下図における赤い長方形の枠は実行結果の画面に表示される範囲を表すものである。
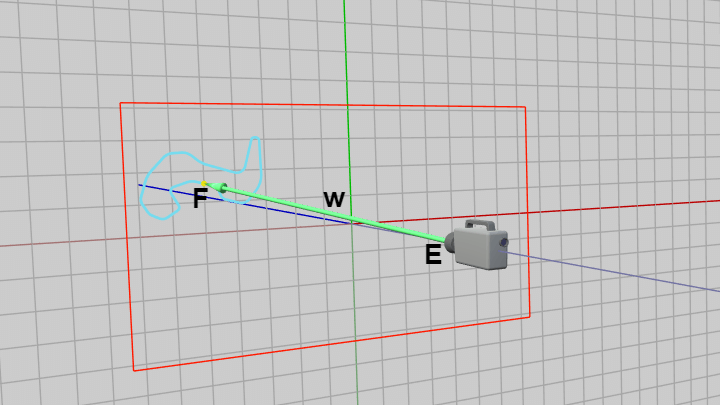
図42 カメラの位置 E からベクトル w だけ離れた位置にMiniMapを配置すれば、画面上では上図41のように表示される (図中の赤い枠は実行画面の表示領域)
したがって下図に示されるように、カメラがどのように移動してもその時点でのカメラの位置からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを置き続ければ、常に画面左上の指定の位置に指定の大きさでMiniMapが表示されることになる (それは毎フレーム カメラと同じだけの移動をMiniMapに行うことと同じである)。
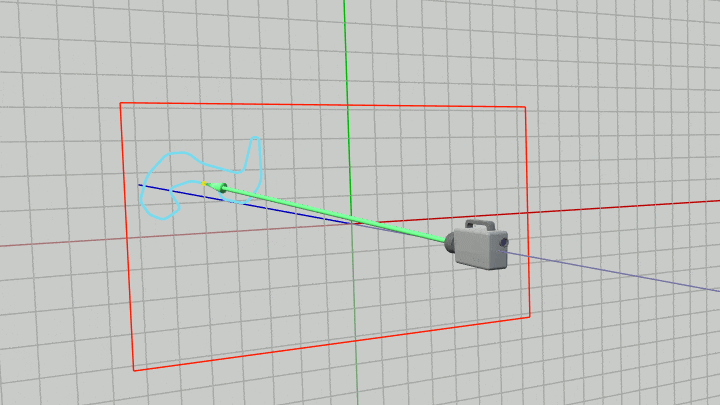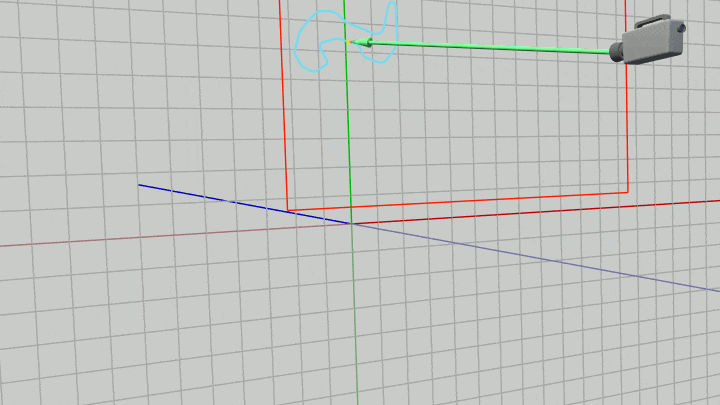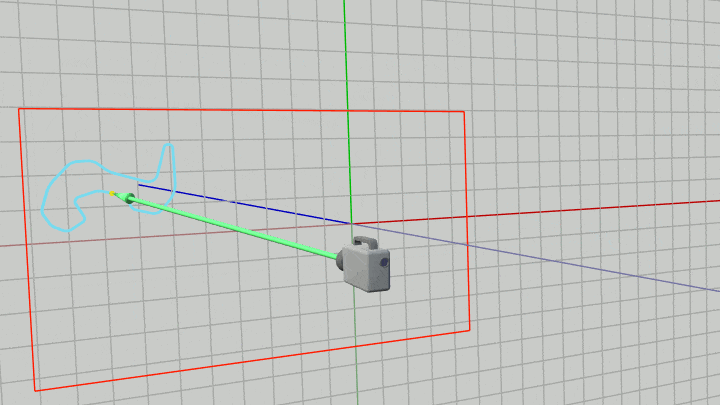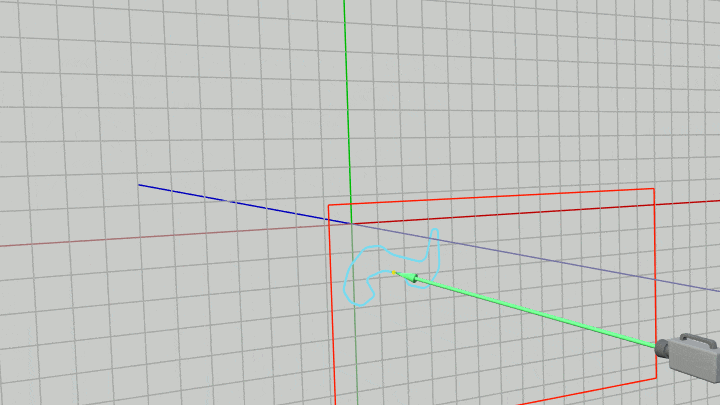
図43 カメラが移動中もカメラの位置から w だけ離れた位置にMiniMapを置き続ける
例えばカメラとMiniMapを上図43のように移動させると実行結果の画面ではMiniMapは以下のように表示される。この実行結果に示されるように、カメラがどのように移動してもMiniMapは常に画面上の同じ位置に同じ大きさで表示されることになる。
では実際にプログラムで確認しよう。
以下のプログラムはサーキット上を走行中の Vehicle をカメラが追跡するものであるが、実行結果の画面左上には常に同じ位置に同じ大きさでVehicleの現在位置を示すMiniMapが表示される。
なお今回は使用するキーを S ではなく J、K に戻している。
J, K : Vehicleの移動
[Code7] (実行結果 図45)
初期化ブロックの E0、F0 は上図42におけるカメラの位置 $E$、MiniMapの位置 $F$ のことであり、i_vEF はその図におけるベクトル $\boldsymbol{\mathsf{w}}$ のことで、この変数はVector3型のインスタンス変数である (Vector2ではない)。
プログラム実行中はMiniMapの大きさは変化しないので、初期化ブロックにおいてその大きさを上記で定めた値に設定している (12行目 ; 設定値は $0.07$ であるが、実際のプログラムではこの値よりもやや小さい値が使われている)。
カメラ移動及びMiniMapの実装は36行目以降である。カメラによる追跡は、Vehicleの現在位置から常に z軸マイナス側に $7.2$ だけ離れた位置で行われる。そして上で述べたようにカメラがどのように移動しても、その時点でのカメラの位置($E$)からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを置き続ければ、画面上では常に指定の位置に指定の大きさで表示されるのであったが、42~43行目がその処理である。
右図47はミニマップ用の迷路である。先程のサーキットの場合と同様にこのミニマップ用の迷路は図46の迷路と形や大きさは同じである (ここでもミニマップ用の下図の迷路を単に MiniMap と呼ぶことにする)。

図46 実際の迷路 
図47 MiniMap 初期状態 (ミニマップ用の迷路であり、実際の迷路と形、大きさは同じ)
今回のプログラムではInspector経由でMiniMapの位置及び大きさを決定する。
実際の迷路移動中においてカメラはXY平面から $20$ だけ離れた位置に置かれており(常にカメラの z座標は $-20$)、このプログラムにおけるカメラの位置も $(0,\ 0, -20)$ として設定されている。
[Code8] (実行結果 図51)
このプログラムは上記の処理のみなので、開始時点では初期状態のMiniMapが表示されるだけである (図48 ; 中央の黄色い点は原点に置かれており、ここでもこの黄色い点をオブジェクト原点と呼ぶことにする)。

図48 プログラム開始時点では初期状態のMiniMapが表示される (初期状態のサイズが大きいため画面には一部しか収まらない)
今回は Hierarchy Window において「MiniMap_Mz」を選択する (図49)。選択後 Inspector において、Position を $(x,\ y,\ z) = (-14.4,\ 3, -0.02)$ とし、Scale を $(x,\ y,\ z) = (0.13,\ 0.13,\ 1)$ とする (図50)。
図49 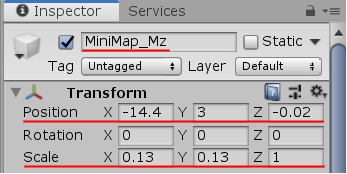
図50
この設定によってMiniMapは下図の状態になるが、実際の迷路移動中においてもこの位置及び大きさでMiniMapが表示されるようにする (MiniMap上の黄色い点はオブジェクト原点でその位置は $(-14.4,\ 3, -0.02)$ )。
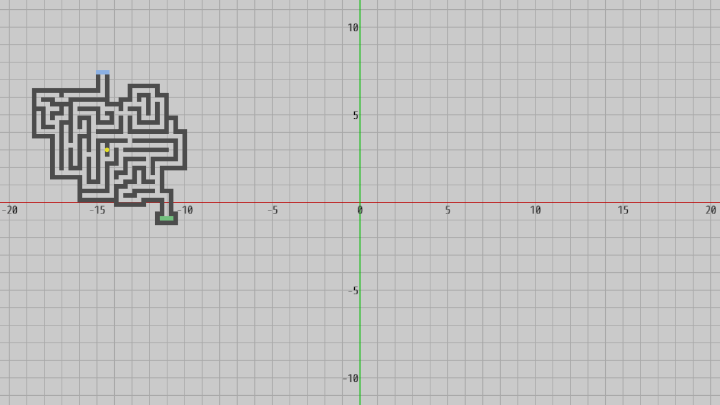
図51
前節同様、迷路内を移動するオブジェクトとして下図52の Square を使用し、MiniMap上でSquareの現在位置を表すオブジェクトとして先程も用いた Dot を使用する。
図52 Square 初期状態 
図31 Dot 初期状態
キー操作は以下のとおり。
H : Squareを左に動かす
L : Square右に動かす
J : Square下に動かす
K : Square上に動かす
[Code9] (実行結果 図53)
このプログラムは前節のCode9にMiniMap用の処理を追加したものである。初期化ブロックにおける i_vEF はCode7と同じくVector3型のインスタンス変数で、実行中におけるカメラの位置からMiniMapの位置(オブジェクト原点)までのベクトルである (E0、F0 はCode8の設定で使われたカメラの位置、及びMiniMapのオブジェクト原点)。
今回も実行中にMiniMapの大きさは変化することはないので初期化ブロックにおいて設定している (10行目 ; 設定値は $0.13$ であるが、実際のプログラムではこの値よりもやや小さい値が使われている)。
カメラ移動及びMiniMapの表示は19行目以降であるが、この部分はわずかな違いを除いてCode7の36行目以降と同じである。
(ここで使用している黒い覆いも、実際には中央に穴の開いた長方形をその z座標を適当にずらして置いているだけである (z座標は $-0.01$)。x座標、y座標には毎フレーム Squareの位置がコピーされる)
今までに2D空間で扱ってきた内容では前節のカメラ移動を除いて、オブジェクトの移動はXY平面上に限定されており、したがって オブジェクトの移動では x座標、y座標のみが変化した。これは2D空間であるから当然といえば当然であるが、本節においてはオブジェクトの位置を設定するにあたって、z座標を含めて考える。今まではほとんど触れることがなかったが、本節で扱う内容においてはこの z座標の設定が非常に重要な役割を担うのである。

カメラの投影モード及びFOVの確認は、まずHierarchy Viewにおいて「Main Camera」を選択し(右図)、カメラ関連の情報をInspector上に表示する。Inspector内に表示されているいくつかの項目の中に「Projection」及び「Field of View」という項目があるので、それぞれの設定値が「Perspective」及び「$60^\circ$」であることを確認する (図1)。
画面のアスペクト比は「Game タブ」のすぐ下に表示されている数値の比である (図2)。


(Unityにおいてプロジェクト作成の際に「3D」を選択している場合は、投影モードとFOVはデフォルトで上記の「Perspective」及び「$60^\circ$」に設定されている)
A) 2D空間の撮影範囲
前節で述べたように2D空間(XY平面)を撮影するカメラは z軸マイナス側に置かれており、z軸プラス方向を向いている (図3)。

図4ではカメラの位置を z軸上で動かして、XY平面からカメラを近づけたり離したりしているが、このときの実行結果の画面が図5である。図に示されるようにカメラをXY平面に近づけると画面に表示される範囲が狭くなり、XY平面から遠ざけると画面に表示される範囲が広がっていく。
(この例ではカメラの位置は z軸上、つまりその x座標、y座標がともに $0$ であるが、以下の解説においてもしばらくの間はこの設定で進める。すなわちカメラの位置は z軸上にあるものとし、実行結果の画面中心には原点が来る)

このようにカメラの位置と実行結果の画面の表示範囲には密接な関係があるわけである。
もちろん具体的な表示範囲、すなわちカメラはXY平面上のどこからどこまでを撮影範囲とするのかを計算することもできるが、その際に必要となるのが上記のアスペクト比及びFOVである。
アスペクト比 (aspect ratio)とはここでは(実行結果の)画面の縦横比のことであり、具体的には「(画面の)横の長さ : 縦の長さ」のことである。したがって、本節冒頭で指定したアスペクト比 $16 : 9$ とは画面の 横 : 縦 が $16 : 9$ であることを意味する (図6)。

FOV (画角、Field of View)とはカメラの撮影範囲を角度で表したものである。FOVは角度を水平方向に測るのか、あるいは垂直方向に測るのかで分かれるが、以下では垂直方向のFOV(vertical FOV)の場合で説明する (Unityのデフォルトではvertical FOVであるため、この講義においてもFOVといえばvertical FOVを指すものとする)。
そして本節冒頭にもあるように以下ではFOVを $60^\circ$ として進める。
ここでXY平面上の原点を $O$、カメラの位置を $E$ とする。上の取り決めによってしばらくはカメラの位置は x座標、y座標ともに $0$ であるから、$E$ は z軸上にある。また y軸プラス側に点 $A$ を置き、y軸マイナス側に $|OA| = |OB|$ となるように点 $B$ を置く (図7)。そしてここではこの2点 $A$、$B$ を、画面に表示される y軸上の上端の点、下端の点とする (下図9)
このとき三角形 $EAB$ は二等辺三角形であり、辺 $EO$ はこの二等辺三角形を二等分する ($|OA| = |OB|$ であるため、点 $A$、$B$ の y座標を $A.\!y$、$B.\!y$ とすれば $B.\!y = -A.\!y$ である)。


図7の状況を真横から見たときのものが図8であるが、このときの $\angle{AEB}$ のことを FOV という (Field of View ; 垂直方向のFOVであるため詳しくは vertical FOV という)。したがって、例えばFOVが $60^\circ$ であるとは上図における $\angle{AEB}$ が $60^\circ$ であることを意味する。
そして上で定めたように、このときの実行結果の画面に表示される y軸の範囲は $B$ から $A$ までであり、$B$ より下、及び $A$ より上は画面には表示されない (図9)。すなわち、FOVとはカメラの撮影範囲(画面に表示される範囲)を表す角度を意味するわけである。
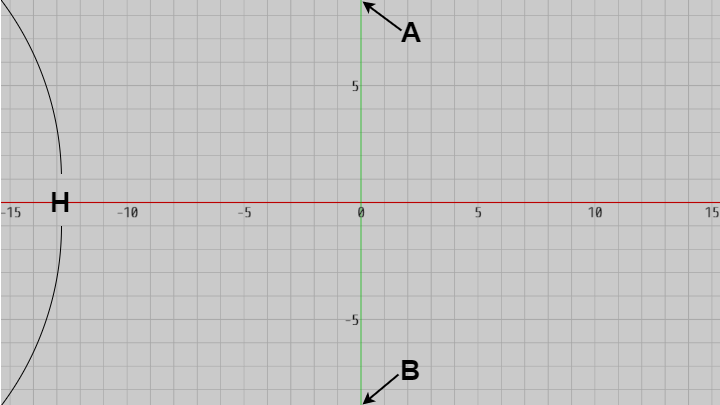

原点 $O$ からカメラの位置 $E$ までの距離を $d$ とし、FOV ($\angle{AEB}$)の半分の角度を $\theta\ (\angle{AEO})$ とする (図10)。右図に示されるように三角形 $AEO$ は直角三角形であるから、\[d\tan{\theta} = H/2\ (=|OA|)\]である。
そして、画面のアスペクト比が $16:9$ であったから、画面の横の長さを $W$ とすれば $W/H = 16/9$ である。したがって、画面の縦の長さ $H$ がわかれば、横の長さ $W$ は\[ W = H \times (16 / 9) \]として求めることができるわけである。
# Code1
最初のプログラムでは実行結果の画面において横半分の長さが $16$、縦半分の長さが $9$ となるようにカメラを配置する (ここでもカメラの位置は x座標、y座標がともに $0$ であり、画面の中心には原点が来る)。プログラムを以下に示す。
[Code1] (実行結果 図11)
if (!i_INITIALIZED)
{
float H2 = 9.0f;
float FOV = 60.0f;
float tanT = Mathf.Tan(FOV * 0.5f * Mathf.Deg2Rad);
float d = H2 / tanT;
MainCamera.transform.position = new Vector3(0, 0, -d);
i_INITIALIZED = true;
}
上図10において角度 $\theta$ はFOVの半分であり、XY平面からカメラまでの距離を $d$ とすれば、画面の縦半分の長さ $H/2$ は\[ d\tan{\theta} = H/2\]として求められるのであった。
そしてここでは画面の縦半分の長さが $9$ としてあらかじめ指定されているので、これを $H/2$ として上記の式から距離 $d$ が求められるわけである ( $d = (H/2)/\tan{\theta}$ )。
プログラム6行目の tanT は $\tan{\theta}$ のことであり、FOV * 0.5 は角度 $\theta$ のことである。
XY平面から $d$ だけ離れた位置にカメラを配置すれば、実行結果の画面において縦半分の長さが $9\ (= H/2)$ となり、(アスペクト比が $16 : 9$ であるから)横半分の長さは自動的に $16$ となる (図11)。
(注 : 前節でも述べたが、プログラムではカメラを表すインスタンス変数 MainCamera への代入処理を省略している。しかし開始時点においてあらかじめ以下の処理が裏側で行われている。
// カメラの取得
MainCamera = GameObject.Find("Main Camera");
# Code2
では次に実行結果の画面において横半分の長さが $12$ になるようにカメラを配置する。プログラムは先程と同様である。
[Code2] (実行結果 図12)
if (!i_INITIALIZED)
{
float aspect = Screen.width / (float)Screen.height;
float W2 = 12.0f;
float H2 = W2 / aspect;
float FOV = 60.0f;
float tanT = Mathf.Tan(FOV * 0.5f * Mathf.Deg2Rad);
float d = H2 / tanT;
MainCamera.transform.position = new Vector3(0, 0, -d);
i_INITIALIZED = true;
}
今回は横半分の長さを $W/2$ とするとき、アスペクト比が $16:9$ であるから縦半分の長さ $H/2$ は\[ (W/2) \div (16/9) = H/2 \]として求められる (プログラム 3~5行目)。縦半分の長さがわかれば、あとはCode1と同様に進めればよい (7行目以降はCode1と同じ)。
なお、アスペクト比を $16:9$ に設定しているからといって実際の画面の横の長さと縦の長さの比が正確に $16:9$ になっているとは限らないことに注意しなければならない ($16:9$ に非常に近い値ではある)。より正確なアスペクト比を求めるには実行画面の横の長さ、縦の長さを表すint型定数 Screen.width、Screen.height (単位はピクセル)を取得して、この2つの長さから計算する必要がある。
例えば上記の3行目では
float aspect = Screen.width / (float)Screen.height;

# Code3
下図13に示されるようにカメラが z軸上の適当な位置に置かれている。ここでは、図14の三角形 Triangle を適当に拡大し、実行結果の画面においてTriangleの上の頂点が画面上端に、Triangleの右の頂点が画面右端に来るようにしてみよう。Triangleは直角二等辺三角形であり、初期状態においては頂点の1つは原点に位置し、残り2つの頂点の位置は $(1,\ 0)$、$(0,\ 1)$ である。


Triangleを拡大せずにそのまま実行すると以下のように表示される (大きさは $1 \times 1$ のまま)。

プログラムは以下のとおり。
[Code3] (実行結果 図16)
if (!i_INITIALIZED)
{
Vector3 E = MainCamera.transform.position;
float d = -E.z;
float aspect = Screen.width / (float)Screen.height;
float FOV = 60.0f;
float tanT = Mathf.Tan(FOV * 0.5f * Mathf.Deg2Rad);
float H2 = d * tanT;
float W2 = H2 * aspect;
Triangle.transform.localScale = new Vector3(W2, H2, 1);
Triangle.transform.position = new Vector2(0, 0);
i_INITIALIZED = true;
}
今回はカメラの位置があらかじめわかっている場合であり、したがってXY平面からカメラまでの距離 $d$ はカメラの位置から求めることができる。すなわち、カメラの z座標がそのままXY平面からカメラまでの距離となる。ただしカメラは z軸マイナス側に置かれているので、z座標はマイナスである。そのため距離 $d$ はその z座標の符号を反転した値、すなわち $d = -E.\!z$ である (4行目)。
距離 $d$ がわかればあとはFOVや $\tan{\theta}$、アスペクト比を使って今までのプログラムと同様に画面の縦半分の長さ、横半分の長さを求め、それらの長さをTriangleのスケール倍率とすればよい (12行目)。

B) スクリーン座標による範囲指定
まずいくつかの取り決めから始める。本節及び次節では「スクリーン座標」や「ワールド座標」及び「ワールド座標系」という用語が使われる。スクリーン座標とはいわゆるピクセルを単位とする画面座標のことである。ワールド座標とは本節と次節においてはXY座標(XY平面上の座標)のことであり、本節及び次節においてワールド座標とあれば単にXY座標の代わりにワールド座標という語を使用しているに過ぎない。同様にここではワールド座標系とはXY平面のことであり、ワールド座標系という語は単にXY平面の代わりに使われているに過ぎない。
また、スクリーン座標は単位がピクセルなので画面上の長さや領域を表す際には $200$ pix、$400 \times 300$ pix のように表記する。
ワールド座標の場合特に決まった単位があるわけではないので、ここでは便宜上「wld」という単位を使用する。すなわち、XY平面上の長さや領域を $12$ wld、$4.8 \times 3.6$ wld のように表記する。
なお、Unityにおいてはスクリーン座標は左下隅が起点である。すなわち、画面左下隅のスクリーン座標が $(0,\ 0)$ である。
(注 : 今までの解説やプログラムではカメラの位置は z軸上、すなわち x座標、y座標はいずれも $0$ であり、したがって画面の中心には必ず原点が来ていたが、ここからはそのような制約はないので画面中心に必ずしも原点が来るとは限らない。例えば下の例では原点の位置は画面中心よりもやや右上である)
今、画面上のスクリーン座標 $M'$ の位置に大きさ $rw \times rh$ pix の長方形を置いたとする (図17)。$M'$ は画面左下隅から右に $mx$、上に $my$ 離れた位置の点である。画面中心のスクリーン座標を $P'(cx,\ cy)$ とし、$P'$ から $M'$ までの横方向の長さを $dx$、縦方向の長さを $dy$ とする。また、画面の横半分の長さを $w/2$、縦半分の長さを $h/2$ とする (以上すべて画面上のスクリーン座標、及びスクリーン座標系で測った長さであり単位は pix である。左下隅が起点 $(0,\ 0)$ )。

上記のスクリーン座標 $M'$ に対応するワールド座標を $M$ とし、スクリーン座標 $P'$ に対応するワールド座標を $P$ とする。また、上図において $w/2$、$h/2$、$rw$、$rh$、$dx$、$dy$ はすべてスクリーン座標系での長さであるが、これらをワールド座標系での長さに変換したものをそれぞれ $W/2$、$H/2$、$RW$、$RH$、$s$、$t$ で表す (図18 ; 以上はすべてワールド座標、及びワールド座標系で測った長さであり単位は wld である)。

カメラの位置があらかじめ決められているものとすれば、XY平面からカメラまでの距離 $d$ はCode3で述べたようにカメラの z座標から求めることができ、$d = -E.\!z$ である。XY平面からカメラまでの距離 $d$ がわかればFOVの半分の角度を $\theta$ とするとき、画面に表示されているXY平面上の縦半分の長さ $H/2$ は、前半の解説にあるように\[d\tan{\theta} = H/2\]である (単位は wld)。
XY平面上の縦半分の長さ $H/2$ は、画面上においては $h/2$ に相当するわけである。すなわち、$H/2$ wld が $h/2$ pix に相当するということであるが、このことから画面上の $1$ pix はXY平面上では何 wld に相当するかを計算できる。つまり、以下の計算を行えばよい。
\[ (H/2)/(h/2) = H/h = WldPerPix \]ここに現れた変数 $WldPerPix$ は、画面上の $1$ pix がXY平面上において何 wld に相当するかを表す変数であり、スクリーン座標とワールド座標の変換において基本となるものである。
この $WldPerPix$ を使って、画面上の長さ $rw$、$rh$、$dx$、$dy$ をそれらに対応するワールド座標系での長さ $RW$、$RH$、$s$、$t$ に変換するには以下の計算を行うだけである。
\begin{align*}&rw \cdot WldPerPix = RW \\ \\&rh \cdot WldPerPix = RH \\ \\&dx \cdot WldPerPix = s \\ \\&dy \cdot WldPerPix = t \\ \\\end{align*}画面の中心を表すスクリーン座標 $P'$ に対応するワールド座標 $P$ はカメラの座標からすぐに求められる (前節 Code7)。すなわちカメラの位置を $E$ とすれば $P = (E.\!x,\ E.\!y)$ である。
上図18において長方形の左下隅の位置を表すワールド座標 $M$ は $P$ から x軸方向に $s$、y軸方向に $t$ だけ離れているから、結局 $M = (P\!.x + s,\ P\!.y + t)$ である (この例では $s, t < 0$ )。
# Code4
まずこのプログラムでは、画面上の $(200,\ 100)$ の位置に大きさ $250 \times 150$ pix の長方形が表示されるようにする ( $(200,\ 100)$ の位置に来るのは長方形の左下隅)。下図19はここで使用する長方形 Rect の初期状態である。Rectは初期状態では1辺の長さが $1$ の正方形であり、左下隅の頂点が原点に位置している。また、今回のプログラムと次のCode5では画面右下に図20のような2組の数値が表示されるが、これはマウスカーソルの現在位置、すなわちマウスカーソルのスクリーン座標が表示されているのである。


プログラムを以下に示す。
[Code4] (実行結果 図21)
if (!i_INITIALIZED)
{
Vector3 E = MainCamera.transform.position;
float d = -E.z;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
float cx = w2;
float cy = h2;
float H2 = d * Mathf.Tan(theta);
float WldPerPix = H2 / h2;
float mx = 200;
float my = 100;
float rw = 250;
float rh = 150;
float dx = mx - cx;
float dy = my - cy;
float s = dx * WldPerPix;
float t = dy * WldPerPix;
float RW = rw * WldPerPix;
float RH = rh * WldPerPix;
Vector2 P = E;
Vector2 M = P + new Vector2(s, t);
Rect.transform.position = M;
Rect.transform.localScale = new Vector3(RW, RH, 1);
i_INITIALIZED = true;
}
上の解説をそのまま実装したものであり、使われている変数も上の解説と同じである。
なお今回のプログラムで注意すべき点は、実行結果の画面に表示されるグリッド線はXY平面上において $1$ ずつの間隔で並んでいるわけではないという点である。
今回表示されるグリッド線はスクリーン座標の起点(左下隅の起点)を基準にして $50$ pix 間隔で並んでいる。つまり、下図の縦のグリッド線は左端から右に向かって $50$ pix の間隔で並んでおり、横のグリッド線は下端から上に向かって $50$ pix の間隔で並んでいる。
これは、Rectが実際に $(200,\ 100)$ の位置に $250 \times 150$ pix の大きさで置かれているかどうかを確認しやすくするためである。

(今回のプログラムも次のプログラムもオブジェクトの位置や大きさをスクリーン座標系で指定するものであるが、これはいわゆるベクターグラフィックスにおいて'力づくで'ラスターグラフィックスを実装しているだけである。そのため厳密ではなく、1 pix 程度の誤差は生じる)
# Code5
続いて、上で使用したRectをプログラム実行中にキー操作によって、位置及び大きさを変えられるようにする。具体的には下図に見られるように、Rectの位置、大きさを 50 pix ずつ変化させる (今回も画面上のグリッド線は左下隅を起点にして 50 pix の間隔で並んでいる)。
キー操作は以下のとおり。
H、J、K、L : Rectの位置を上下左右に 50 pix ずつ動かす (H、L が横方向、J、K が縦方向の移動)
Shift + H、J、K、L : Rectの大きさを 50 pix ずつ変化させる (H、L が横方向の調整、J、K が縦方向の調整)
[Code5] (実行結果 図22)
if (!i_INITIALIZED)
{
Vector3 E = MainCamera.transform.position;
float d = -E.z;
float FOV = 60.0f;
float theta = FOV * 0.5f * Mathf.Deg2Rad;
float w2 = Screen.width * 0.5f;
float h2 = Screen.height * 0.5f;
i_cx = w2;
i_cy = h2;
float H2 = d * Mathf.Tan(theta);
i_WldPerPix = H2 / h2;
i_locX = 1;
i_locY = 1;
i_width = 2;
i_height = 2;
i_INITIALIZED = true;
}
bool shift = THUtil.IsShiftDown();
if (Input.GetKeyDown(KeyCode.H))
{
if (shift) { i_width--; }
else { i_locX--; }
}
else if (Input.GetKeyDown(KeyCode.L))
{
if (shift) { i_width++; }
else { i_locX++; }
}
else if (Input.GetKeyDown(KeyCode.J))
{
if (shift) { i_height--; }
else { i_locY--; }
}
else if (Input.GetKeyDown(KeyCode.K))
{
if (shift) { i_height++; }
else { i_locY++; }
}
i_locX = Mathf.Clamp(i_locX, 0, 20);
i_locY = Mathf.Clamp(i_locY, 0, 20);
i_width = Mathf.Clamp(i_width, 1, 20);
i_height = Mathf.Clamp(i_height, 1, 20);
float mx = i_locX * 50;
float my = i_locY * 50;
float rw = i_width * 50;
float rh = i_height * 50;
float dx = mx - i_cx;
float dy = my - i_cy;
float RW = rw * i_WldPerPix;
float RH = rh * i_WldPerPix;
float s = dx * i_WldPerPix;
float t = dy * i_WldPerPix;
Vector2 P = MainCamera.transform.position;
Vector2 M = P + new Vector2(s, t);
Rect.transform.position = M;
Rect.transform.localScale = new Vector3(RW, RH, 1);
今回はプログラム実行中にもスクリーン座標とワールド座標の変換を行うので、初期化ブロックではその処理の際に必要となる $cx$、$cy$ (画面中心を表すスクリーン座標)、$WldPerPix$ などをインスタンス変数にしている (10~14行目 ; 画面のサイズが変化したり、カメラが動くことはないのでこれらの変数の値はプログラム実行中常に同じである)。
16~19行目の i_locX、i_locY、i_width、i_height はRectの(左下隅の)位置、及びRectの大きさを表すためのインスタンス変数で、上図22のグリッド線において何マス目の位置か、あるいは何マス分の大きさかを表している。例えばここでは i_locX、i_locY はともに $1$ であるが、これは左下隅から右に $1$ マス、上に $1$ マス分離れた位置にRectが(Rectの左下隅)が置かれることを意味する。i_width、i_height はともに $2$ であるが、これは開始時点におけるRectの大きさが縦横ともに $2$ マス分であることを意味する。
これらのインスタンス変数の値をスクリーン座標系での値に変換するには、これらのインスタンス変数に $50$ を掛ければよい。すなわちプログラム開始時点においては、Rectの左下隅の位置は $(50,\ 50)$ であり、その大きさは $100 \times 100$ である。
26~45行目のキー操作ではShiftキーが押されて入れば i_width、i_height を変化させ(大きさの変化)、押されていなければ i_locX、i_locY を変化させる (位置の変化)。これらのインスタンス変数にはいずれも下限、上限があり、例えば i_locX、i_locY の下限は $0$ なのでRectの左下隅の位置を画面左下隅よりも左あるいは下に移動させることはできない。また、i_width、i_height の上限は $20$ なのでRectの縦横の長さを $1000$ pix よりも大きくすることはできない。
52行目以降の処理は先程のプログラムと同じである。
C) 画面において手前に表示されるオブジェクト
下図は2つの長方形 Green 及び Blue の初期状態である。いずれも初期状態では大きさは同じでありその中心が原点に置かれている。

この2つの長方形をややずらして表示したときの結果が下図25であり、2つの長方形が重なっているが、ここではGreenが手前に表示されている。
このときのXY平面及びカメラを離れた位置から見たときのものが図26である。図に示されるようにカメラの位置は $(0,\ 0, -10)$ であるから、XY平面からカメラまでの距離は $10$ である。


上図25の場合は2つの長方形はいずれもXY平面上に置かれているのでその z座標は $0$ である。したがって、カメラからの距離はいずれも $10$ である。上図の場合はたまたまGreenが表示されているが、オブジェクトが重なっている場合、カメラからの距離が近い方のオブジェクトが手前に表示される (これは設定によって変えることができるが、デフォルトではカメラからの距離が近い方が手前に表示される)。
上の状況ではいずれも z座標は $0$ であるが、例えばここでBlueの z座標を $-0.01$ にしたとしよう。この場合にはBlueはカメラに $0.01$ だけ近づいたわけである。このときの実行結果が下図27であるが、BlueはGreenよりも $0.01$ だけカメラに近い位置に置かれているので、確かにBlueが手前に表示されるようになる。


この状況からGreenの z座標を $-0.02$ にしたとしよう。この場合両者の z座標は Blue $-0.01$、Green $-0.02$ となるので、今度はGreenの方がカメラに近くなるわけである。図28はこのときの実行結果であるが、またGreenが手前に表示されるようになっている。
そしてここで重要なのが上図25、図27、図28では長方形の z座標を $0.01$ あるいは $0.02$ だけずらしているが、見た目ではその違いがわからないという点である。つまり、2Dオブジェクトを $z=0$ のXY平面上に置くのも、z座標を $0.01$ や $0.02$ だけずらして置くのも置かれる位置や大きさは結果的には変わらない、しかし、カメラにわずかでも近いオブジェクトの方が必ず手前に表示されるのである。
今述べたことはおそらくは自明なことであったろう。しかし、これから実装するミニマップや次節におけるテキストの表示などは今述べたことの応用に過ぎない。以下に展開する実装方法は、ミニマップやテキストの実装方法としては非常に簡単で応用のしやすいものである (ただし以下で解説する方法は2D空間限定の方法である)。
# Code6
以下、本節後半では画面上におけるミニマップの表示について見ていく。まずは前節のCode8で用いたサーキットの例を用いて進める。前節でも触れたが、ここで使うサーキット(下図29)はそのサイズが大きいため、今回のプログラムではサーキットが画面全体に収まるようにするために、カメラをXY平面からやや離して置いている。

ここでもサーキット上を走行するオブジェクトとして以下の Vehicle を使用する (図30)。またミニマップ上でVehicleの位置を表すオブジェクトとして右図の Dot を使用する (下図のグリッド線の間隔は適当であり、その間隔は必ずしも $1$ ではない)。


さらにミニマップ用のサーキットとして、上記のサーキットと全く同じ形状のものを用意する。ただし下図に示されるように形は同じであり、全体の大きさも同じではあるが、路面の幅などは狭くなっている。
以下このミニマップ用に使われるサーキットを単に MiniMap と呼ぶことにする。またMiniMapの中心部分に黄色い点があるが、この黄色い点はMiniMapの初期状態では原点に位置している。MiniMapの初期状態において原点に置かれているこの黄色い点をここでは「オブジェクト原点」と呼ぶことにする。

以下のプログラムは前節のCode8を多少変更して、上記のMiniMap及びDotの運動を追加したものである。
[Beta6] (実行結果 図33)
if (!i_INITIALIZED)
{
Curve = ConstructCurve();
t = 0.0f;
i_MOVE = true;
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (!i_MOVE) { return; }
t += 0.001f;
if(t > 1.0f) { t -= 1.0f; }
Vector2[] vrr = Curve.ComputePositionAndTangent(t);
Vector2 pos = vrr[0];
Vector2 dir = vrr[1];
Quaternion rot = TH2DMath.CalcRotation_V1toV2(Vector2.up, dir);
Vehicle.transform.position = new Vector3(pos.x, pos.y, -0.01f);
Vehicle.transform.rotation = rot;
Dot.transform.position = new Vector3(pos.x, pos.y, -0.01f);
MiniMap.transform.position = new Vector3(0, 0, -0.01f);
27行目までは前節のCode8と同様の処理である。前節のCode8では J、K キーによってVehicleを進めたり、戻したりすることができたが、今回は常にVehicleはサーキット上を走り続けるように変更されている。このVehicleの移動も S キーによって移動、停止の切り替えが行えるようになっている。
29~30行目が追加部分である。追加した処理の内容は、Dotの位置を毎フレーム Vehicleと同じ位置に移動させ、MiniMapを初期状態のまま配置ているだけである。ただしプログラムにあるように、Vehicle及び Dot、MiniMap の z座標はいずれも $-0.01$ となっており、これによってXY平面上に置かれたサーキット($z = 0$)よりも手前に表示されるようになる。
Dotは毎フレーム Vehicleと同じ位置に移動することになるので、下図に示されるようにDotは常にVehicleと一体となって移動することになる (見やすさのためにDotの位置はわずかにずらし、Dotを赤、MiniMapを水色を変えている。実際にはVehicleとDotは完全に重なってしまう)。

ここからMiniMap及びDotに対していくつかの変換を行うが、ここからの一連の流れは重要である。
上のBeta6では本来のサーキットとミニマップ用のサーキット(MiniMap)が同じ位置に置かれており、さらにVehicleとDotも常に同じ位置にあるためこれらのオブジェクトは常に重なっていた。例えば上記のプログラムにおいてMiniMap及びDotの位置を毎フレーム x軸方向に $-5$ だけずらすと、すなわち29行目以降を以下のように変更すると、
Vector3 mv = new Vector3(-5, 0, 0); Dot.transform.position = new Vector3(pos.x, pos.y, -0.03f) + mv; MiniMap.transform.position = new Vector3(0, 0, -0.02f) + mv;
このときのMiniMapのオブジェクトの原点(黄色い点)の x座標、y座標は $(-5,\ 0)$ である。下図のグリッド線は $1.5$ 倍に拡大されているため、グリッド線の間隔は $1.5$ である ($1$ ではない)。

MiniMapがどこに置かれてもDotは常にMiniMap上を移動するので、この2つのオブジェクトには親子関係を設定する方が自然である。例えば上記では毎フレーム DotとMiniMapの両方に x軸方向の $-5$ の移動である mv が加算されているが、親子関係を設定すればこういった同じ加算を2つのオブジェクトに対してする必要がなくなる。
DotとMiniMapに親子関係を設定した場合において、両者を x軸方向に $-5$ だけずらして置く先程の処理は以下のように記述される (今回は親子関係が設定されているのでDot及びMiniMapの位置設定には position ではなく localPosition が使われている)。
Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f); Vector3 mv = new Vector3(-5, 0, 0); MiniMap.transform.localPosition = new Vector3(0, 0, -0.02f) + mv;
さらにこの状態からMiniMap及びDotの大きさを半分にする。両者には親子関係が設定されているので、このスケールも親オブジェクトであるMiniMapに対してのみ実行すればよい。具体的には以下のとおり。
Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f); Vector3 mv = new Vector3(-5, 0, 0); float s = 0.5f; MiniMap.transform.localPosition = new Vector3(0, 0, -0.02f) + mv; MiniMap.transform.localScale = new Vector3(s, s, 1);
この変更後の実行結果が以下の図35である。MiniMapとDotの大きさが縮小されているが、これは上図34の状態からMiniMapのオブジェクト原点のある $(-5,\ 0)$ を中心に $0.5$ 倍縮小した結果である (スケールは必ずオブジェクト原点を中心に行われる)。
なお下図の実行結果においてもグリッド線の間隔は $1.5$ である。

次のプログラムは今までに述べてきたことをまとめたものである。
サーキット上を一定の速度でVehicleが走行している。Vehicleの現在位置を表示するためのMiniMapがXY平面から $0.02$ だけずらして置かれており ($z=-0.02$)、その子オブジェクトとしてDotがMiniMapから z軸方向マイナス側に $0.01$ だけずらして置かれている ($z=-0.03$)。そして両者には $0.5$ 倍のスケールが実行されている。
さらにここでは、以下のキー操作によってMiniMapを上下左右に移動させる。
H : MiniMapを左に動かす
L : MiniMapを右に動かす
J : MiniMapを下に動かす
K : MiniMapを上に動かす
プログラムは以下のとおり。
[Code6] (実行結果 図36)
if (!i_INITIALIZED)
{
Curve = ConstructCurve();
t = 0.0f;
i_MOVE = true;
Dot.transform.SetParent(MiniMap.transform);
MiniMap.transform.localPosition = new Vector3(0, 0, -0.02f);
MiniMap.transform.localScale = new Vector3(0.5f, 0.5f, 1);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
i_MOVE = !i_MOVE;
}
if (!i_MOVE) { return; }
t += 0.001f;
if (t > 1.0f) { t -= 1.0f; }
Vector2[] vrr = Curve.ComputePositionAndTangent(t);
Vector2 pos = vrr[0];
Vector2 dir = vrr[1];
Quaternion rot = TH2DMath.CalcRotation_V1toV2(Vector2.up, dir);
Vehicle.transform.position = new Vector3(pos.x, pos.y, -0.01f);
Vehicle.transform.rotation = rot;
Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f);
Vector3 mp = MiniMap.transform.localPosition;
if (Input.GetKey(KeyCode.H))
{
mp.x -= 0.05f;
}
else if (Input.GetKey(KeyCode.L))
{
mp.x += 0.05f;
}
if (Input.GetKey(KeyCode.J))
{
mp.y -= 0.05f;
}
else if (Input.GetKey(KeyCode.K))
{
mp.y += 0.05f;
}
MiniMap.transform.localPosition = mp;
初期化ブロックの8行目ではDotとMiniMapの親子関係を設定している。このプログラムではMiniMapは $0.5$ 倍にスケールされるが、プログラム実行中においてはその倍率に変化はないのでその処理は初期化ブロックで行われる (11行目)。また今回は開始時点においてMiniMapのオブジェクト原点の位置は $(0,\ 0)$ に置かれた状態から始まる。そして上で見てきたようにMiniMapはVehicleやサーキットよりも手前に表示するために z座標を $-0.02$ としている (10行目。Vehicleの z座標は $-0.01$、サーキットの z座標は $0$)。
上記ではいくつかのコードによってMiniMap(及びDot)の位置や大きさを変えてきたが、このプログラムにおいては35行目以降がその処理に該当する。Dotに対する変換内容(Vehicleと同じ位置に移動させ、その z座標を $-0.01$ にする処理)は変わらないが、それ以降の部分でキー操作によってMiniMapを動かす処理を入れている。
指定のキーがおされている間は x軸方向、y軸方向に $0.05$ ずつ移動するが、このときに変化するのはMiniMapの x座標、y座標のみであり、z座標は初期化ブロックで設定した値 $-0.02$ のままである。毎フレーム 37行目でMiniMapの現在位置 mp を取得し、この mp の x座標、y座標に移動分を加算している。つまり、変更されるのは x座標、y座標のみなので z座標の値は常に変わることはない (37行目の mp の型をVector2にしてもエラーにはならないが、Vector2にしてしまうと55行目で再度MiniMapにこの変数をセットした際に z座標の情報が失われてしまうので注意が必要である)。
このプログラムで目的としていることは、MiniMapを適当な大きさに変更しプログラム実行中にどのように移動させても、サーキット上を走行するVehicleの現在位置がMiniMap上にDotとして表示され、さらにMiniMapが常に画面の手前に表示されるようにするという点である。
下図の実行結果に示されるようにMiniMapを適当な大きさに変更し、適当な位置に移動させても、サーキット上のVehicleの現在位置がMiniMap上には常に表示され、どの位置においてもMiniMapは画面の一番手前に来る。そして重要なことは各オブジェクトが重なったときの前後関係(どれが手前に表示されるか)の決定は z座標をわずかにずらすという形で行われているのである。

また、今回の実装において毎フレーム のVehicle及びDotに対する平行移動の内容は同じである (32~35行目 ; ともに x座標、y座標が pos.x、pos.y で、z座標は $-0.01$ )。平行移動の内容が同じなのは、サーキット上におけるVehicleの現在位置をMiniMap上に表示するという目的のためである。
Vehicle.transform.position = new Vector3(pos.x, pos.y, -0.01f); ... ... ... ... Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f);
平行移動の内容は同じであるが、VehicleとDotは同じ位置に置かれるわけではない (つまり両者が重なって表示されたりはしない)。それはDotがMiniMapの子オブジェクトであり、MiniMapに対する変換の影響を受けるためである。
もし読者がこのあたりの理解があいまいなのであれば、再度MiniMapが何の変換も受けていないBeta6に戻って考えるとよい。Beta6ではMiniMapは初期状態であり、初期状態においてはMiniMapはサーキットと形、大きさが同じであった。その状況ではVehicleと同じ位置に毎フレーム Dotを移動させると(平行移動の内容を同じにすると)、VehicleとDotの位置は常に同じになるため、両者は重なって表示されたのであった (図33)。
重要なのはそこからの一連の手続きである。そこからいろいろな'細工'をすることによって、上図36のようなMiniMapを実現しているわけである。そしてその根底にあるのがオブジェクトの親子関係と z座標のずらしなのである。
なお1点補足しておこう。
上のプログラムではMiniMapの位置の変更は行われるが、大きさは常に同じであり変化しない。もし、MiniMapの大きさをスケールによって変化させる場合、MiniMapの拡大縮小はMiniMapのオブジェクト原点を中心にして行われる (これは他のオブジェクトでも同じである)。実際、下図はMiniMapをある位置から動かさずに、その大きさだけを変化させているときの様子であるが、オブジェクト原点(黄色い点)を中心に拡大縮小が行われていることがわかるであろう。

# Code7
あとは画面上に表示されるMiniMapの位置、及び大きさを決めるだけである。一番簡単な方法はUnityのInspectorを使う方法であり、以下その方法で進める。
上でも触れたが、上記のCode6ではサーキット全体が画面に収まるようにカメラはやや離れた位置に置かれていた。今回はカメラの位置をレース用の位置に戻すが、その位置はXY平面から $7.2$ だけ離れている。つまり サーキット上をVehicleが走行する間は、カメラはXY平面から $7.2$ だけ離れた位置でVehicleの追跡を行う (常にカメラの z座標は $-7.2$)。
MiniMapの位置及び大きさを決定するために、まずカメラをXY平面から $7.2$ だけ離れた位置に配置する。その際カメラの x座標、y座標はどこでもよいが、ここでは簡単のためともに $0$、すなわち $(x,\ y,\ z) = (0,\ 0, -7.2)$ の位置にカメラを配置する。
このカメラ配置でプログラムを実行し、初期状態のMiniMapのみを表示すると実行結果の画面は下図のような表示になる (今回はカメラをXY平面に近づけているので初期状態のMiniMapはその一部しか画面に入らない)。

ここからMiniMapの位置及び大きさの調整を始める。
Unity画面上において Hierarchy Window 内にある「MiniMap_Cr」を選択する (図39)。選択すると Inspector 内にMiniMapに関する情報が表示されるが、このInspector内の Transform という項目にある「Position」「Scale」の各値をここでは変更する (図40)。
Scale はMiniMapの大きさを調整するためのものであり、今回はMiniMapを $0.07$ 倍に縮小するので、x 及び y に $0.07$ を入力する。Position はMiniMapの位置を調整するためのものであるが、今回は画面左上にMiniMapを表示するので x に $-5$、y に $1.6$ を、さらに常に画面手前に表示されるように z に $-0.02$ を入力する。これによってMiniMapのオブジェクト原点(黄色い点)が $(-5,\ 1.6, -0.02)$ の位置にくる。


この調整によってMiniMapは以下のように表示されるが、これをMiniMapの正式な位置、大きさとし、今回のプログラムでは実行中 常にMiniMapが下図の状態で画面上に表示されるようにする。
常に画面上の指定の位置に指定の大きさでMiniMapが表示されるようにするためには、さらにもう1つだけ準備が必要になる。

上図41の状況を離れた位置から見たときのものが下図42である。図中の $E$ はカメラの位置であり、ここでは $E = (0,\ 0, -7.2)$ である。$F$ はMiniMapのオブジェクト原点であり、先程定めたように $F = (-5,\ 1.6, -0.02)$ である (MiniMapには z座標の'ずらし'が行われている)。
また図中には緑色のベクトルがあるが、これは始点を $E$、終点を $F$ とするベクトルであり、以下このベクトルを $\boldsymbol{\mathsf{w}}$ で表す。
下図の状況を簡単にいうと、カメラの位置 $E$ からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを配置すれば、画面上では上図41のように表示されるということである (MiniMapにはスケールが行われているものとする)。下図における赤い長方形の枠は実行結果の画面に表示される範囲を表すものである。

したがって下図に示されるように、カメラがどのように移動してもその時点でのカメラの位置からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを置き続ければ、常に画面左上の指定の位置に指定の大きさでMiniMapが表示されることになる (それは毎フレーム カメラと同じだけの移動をMiniMapに行うことと同じである)。

例えばカメラとMiniMapを上図43のように移動させると実行結果の画面ではMiniMapは以下のように表示される。この実行結果に示されるように、カメラがどのように移動してもMiniMapは常に画面上の同じ位置に同じ大きさで表示されることになる。
図44 カメラとMiniMapを上図43のように移動させたときの実行結果の画面
では実際にプログラムで確認しよう。
以下のプログラムはサーキット上を走行中の Vehicle をカメラが追跡するものであるが、実行結果の画面左上には常に同じ位置に同じ大きさでVehicleの現在位置を示すMiniMapが表示される。
なお今回は使用するキーを S ではなく J、K に戻している。
J, K : Vehicleの移動
[Code7] (実行結果 図45)
if (!i_INITIALIZED)
{
Curve = ConstructCurve();
t = 0.0f;
Vector3 E0 = new Vector3(0, 0, -7.2f);
Vector3 F0 = new Vector3(-5.0f, 1.6f, -0.02f);
i_vEF = F0 - E0;
Dot.transform.SetParent(MiniMap.transform);
MiniMap.transform.localScale = new Vector3(0.07f, 0.07f, 1.0f);
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.K))
{
t += 0.001f;
if (t > 1.0f) { t -= 1.0f; }
}
else if (Input.GetKey(KeyCode.J))
{
t -= 0.001f;
if (t < 0.0f) { t += 1.0f; }
}
Vector2[] vrr = Curve.ComputePositionAndTangent(t);
Vector2 pos = vrr[0];
Vector2 dir = vrr[1];
Quaternion rot = TH3DMath.CalcRotation_V1toV2(Vector2.up, dir);
Vehicle.transform.position = new Vector3(pos.x, pos.y, -0.01f);
Vehicle.transform.rotation = rot;
Vector3 E = pos;
E.z = -7.2f;
MainCamera.transform.position = E;
Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f);
Vector3 F = E + i_vEF;
MiniMap.transform.localPosition = F;
初期化ブロックの E0、F0 は上図42におけるカメラの位置 $E$、MiniMapの位置 $F$ のことであり、i_vEF はその図におけるベクトル $\boldsymbol{\mathsf{w}}$ のことで、この変数はVector3型のインスタンス変数である (Vector2ではない)。
プログラム実行中はMiniMapの大きさは変化しないので、初期化ブロックにおいてその大きさを上記で定めた値に設定している (12行目 ; 設定値は $0.07$ であるが、実際のプログラムではこの値よりもやや小さい値が使われている)。
カメラ移動及びMiniMapの実装は36行目以降である。カメラによる追跡は、Vehicleの現在位置から常に z軸マイナス側に $7.2$ だけ離れた位置で行われる。そして上で述べたようにカメラがどのように移動しても、その時点でのカメラの位置($E$)からベクトル $\boldsymbol{\mathsf{w}}$ だけ離れた位置にMiniMapを置き続ければ、画面上では常に指定の位置に指定の大きさで表示されるのであったが、42~43行目がその処理である。
図45 Code7 実行結果 (ここではMiniMapやDotの色を本来の色に戻している。またオブジェクト原点は表示していない)
# Code8
前節のCode9は下図46に示される迷路内の移動をカメラで追跡するというものであったが、このプログラムと次のプログラムではこの迷路内の移動にミニマップを追加する。しかし行うことは上記のCode6、Code7と同じである。右図47はミニマップ用の迷路である。先程のサーキットの場合と同様にこのミニマップ用の迷路は図46の迷路と形や大きさは同じである (ここでもミニマップ用の下図の迷路を単に MiniMap と呼ぶことにする)。


今回のプログラムではInspector経由でMiniMapの位置及び大きさを決定する。
実際の迷路移動中においてカメラはXY平面から $20$ だけ離れた位置に置かれており(常にカメラの z座標は $-20$)、このプログラムにおけるカメラの位置も $(0,\ 0, -20)$ として設定されている。
[Code8] (実行結果 図51)
if (!i_INITIALIZED)
{
MiniMap.SetMatrix(THMatrix3x3.identity);
i_INITIALIZED = true;
}
このプログラムは上記の処理のみなので、開始時点では初期状態のMiniMapが表示されるだけである (図48 ; 中央の黄色い点は原点に置かれており、ここでもこの黄色い点をオブジェクト原点と呼ぶことにする)。

今回は Hierarchy Window において「MiniMap_Mz」を選択する (図49)。選択後 Inspector において、Position を $(x,\ y,\ z) = (-14.4,\ 3, -0.02)$ とし、Scale を $(x,\ y,\ z) = (0.13,\ 0.13,\ 1)$ とする (図50)。


この設定によってMiniMapは下図の状態になるが、実際の迷路移動中においてもこの位置及び大きさでMiniMapが表示されるようにする (MiniMap上の黄色い点はオブジェクト原点でその位置は $(-14.4,\ 3, -0.02)$ )。

# Code9
では迷路移動中に上記で設定したMiniMapが、常に画面の指定の位置に指定の大きさで表示されるかを確認しよう。前節同様、迷路内を移動するオブジェクトとして下図52の Square を使用し、MiniMap上でSquareの現在位置を表すオブジェクトとして先程も用いた Dot を使用する。


キー操作は以下のとおり。
H : Squareを左に動かす
L : Square右に動かす
J : Square下に動かす
K : Square上に動かす
[Code9] (実行結果 図53)
if (!i_INITIALIZED)
{
Square.SetPosition(c_StartPosition);
Vector3 E0 = new Vector3(0, 0, -20);
Vector3 F0 = new Vector3(-14.4f, 3.0f, -0.02f);
i_vEF = F0 - E0;
Dot.transform.SetParent(MiniMap_Mz.transform);
MiniMap.transform.localScale = new Vector3(0.13f, 0.13f, 1.0f);
i_INITIALIZED = true;
}
MoveSquare();
Vector2 pos = Square.transform.position;
Vector3 E = new Vector3(pos.x, pos.y, -20.0f);
MainCamera.transform.position = E;
Dot.transform.localPosition = new Vector3(pos.x, pos.y, -0.01f);
Vector3 F = E + i_vEF;
MiniMap.transform.localPosition = F;
このプログラムは前節のCode9にMiniMap用の処理を追加したものである。初期化ブロックにおける i_vEF はCode7と同じくVector3型のインスタンス変数で、実行中におけるカメラの位置からMiniMapの位置(オブジェクト原点)までのベクトルである (E0、F0 はCode8の設定で使われたカメラの位置、及びMiniMapのオブジェクト原点)。
今回も実行中にMiniMapの大きさは変化することはないので初期化ブロックにおいて設定している (10行目 ; 設定値は $0.13$ であるが、実際のプログラムではこの値よりもやや小さい値が使われている)。
カメラ移動及びMiniMapの表示は19行目以降であるが、この部分はわずかな違いを除いてCode7の36行目以降と同じである。
図53 Code9 実行結果 (ここではMiniMapのオブジェクト原点は表示していない)
(ここで使用している黒い覆いも、実際には中央に穴の開いた長方形をその z座標を適当にずらして置いているだけである (z座標は $-0.01$)。x座標、y座標には毎フレーム Squareの位置がコピーされる)
© 2020-2025 Redpoll's 60 (All rights reserved)