Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-26
第2章 2D空間におけるオブジェクトの運動
$§$2-26 円と直線による補間曲線 2
本節ではカスタムライブラリーのクラスを利用して、前節の方法によって作成された補間曲線上の位置や接線をパラメーターを介して取得することについて見ていく。
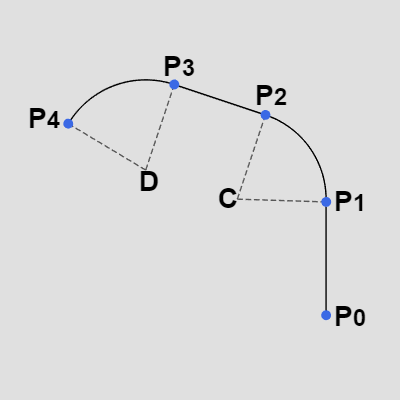
図1 ここで扱う補間曲線は線分と弧から構成されるものであるが、曲線を構成するこれらの線分や弧を以下では「区間」と呼ぶことにする。例えば右図の曲線は2つの線分と2つの弧から構成されるので、この曲線は4つの区間から成るわけである。
便宜上 $P_0$~$P_1$ の区間を 区間0、$P_1$~$P_2$ の区間を 区間1 のように表記する。
さらにここで区間を表すためのカスタムライブラリーのクラス Segment を用意する。Segment クラスは補間曲線を構成する各区間を表すクラスであり、区間が線分である場合と弧である場合によって使用するコンストラクタが異なる。
例えば右図の区間0は線分であり、具体的には線分 $P_0P_1$ であるが、区間が線分である場合にはコンストラクタの引数にその線分の両端の点を指定する。
区間1は弧であり、弧の両端の点は $P_1$、$P_2$、そして弧の中心(弧を含む円周の中心)は $C$ である。区間が弧である場合、コンストラクタにはその弧の両端の点及び弧の中心を指定する (引数の順序は2つの端点、弧の中心の順)。
上図の曲線は4つの区間によって構成されるが、この曲線をSegmentによって定義すると次のように記述される (ここでは各SegmentをListクラスにセットしている)。
曲線をSegmentによって定義する場合には必ず区間0、区間1、区間2、$...$ のように順番にセットしていく必要がある。Segment のコンストラクタにおいてもその最初の2つの引数には区間の両端点を指定するが、この両端点も曲線上での順序通りに指定しなければならない (例えば区間0の場合はコンストラクタの引数は $P_0$、$P_1$ の順であり、$P_1$、$P_0$ の順にはできない)。
前節における補間曲線は、実際にはいくつかの制御点とそれらの点における接線をもとにして作成された。例えば上図1の場合は下図2の制御点及び接線をもとに作成されている (図3は図2の制御点及び接線から構成された補間曲線であり、これは上図1のものと同じである)。
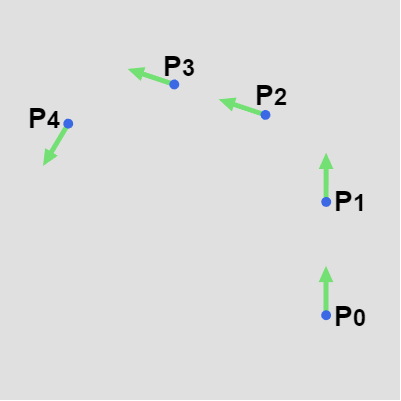
図2 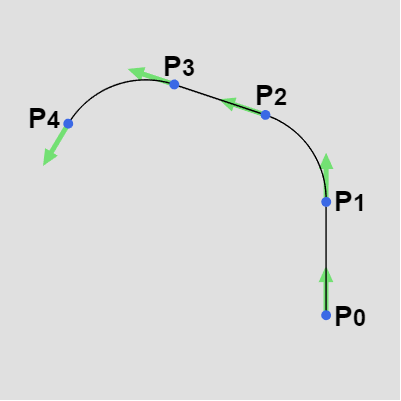
図3 図2の制御点及び接線から構成された補間曲線(図1のものと同じ)
そして制御点及び接線による補間曲線の作成はプログラムでは次のように記述されていた (前節のものとは多少書き方を変えてある)。
このプログラムでは制御点は arrP[i]、それらの点における接線は arrT[i] であり、冒頭の GetPositionArray()、GetTangetnArray() は曲線を構成する制御点及び接線を取得するためのメソッドである。
前節においては上記13行目の InterpolatePQ(..) は補間曲線を作成するためのメソッドとして使われており、このメソッドの中で線分や弧の描画まで行われていた。しかし本節では補間曲線上の位置や接線の方向をパラメーターを介して取得することが目的であるため、補間曲線の描画自体は必要ではない。そのためこの InterpolatePQ(..) から余計な処理を削除して必要な処理だけを記述した InterpolatePQ_Data(..) というメソッドをここでは使うことにする。これによって上のプログラムは以下のように変更される。
InterpolatePQ_Data(..) (14行目)の最後の引数には List<Segment> 型の segments という変数が指定されているが、この segments には補間曲線をSegmentによって定義したときの各Segmentのデータがセットされる。
InterpolatePQ_Data(..) の具体的な内容を以下に示す。
冒頭のifブロック(5行目)は2つの隣り合う制御点 P、Q が線分区間となる場合である。引数 R3 には、P から v の方向に引いた直線と Q から w の方向に引いた直線の交点がセットされているが、2つの制御点及び接線が適切な位置関係にない場合にはこの R3 の z座標には $-1$ がセットされ、その場合には P と Q は線分で結ばれるのであった (前節参照)。
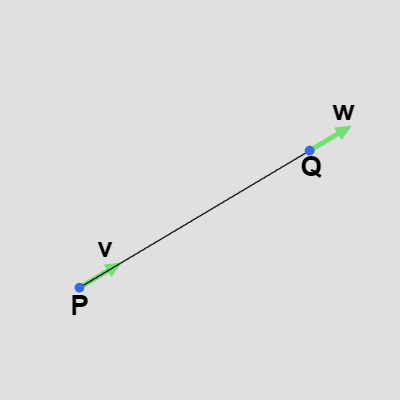
図4 PQ間を線分で結ぶためには v、w の向きを、PからQの方向と同じにすればよい この他にも P、Q が線分で結ばれる場合があり、それは右図に示されるようにもともとこの区間を線分として指定している場合である。 この場合には P の接線 v 及び Q の接線 w の方向が同じであり、かつ P、Q を結ぶベクトルも v、w の方向に等しくなる。このようなケースでは CalcIntersectionOf2Lines(P, v, Q, w) の戻り値は線分 $PQ$ の中点となり (2-24節)、したがって、InterpolatePQ_Data(..) の引数 R3 の値はこの場合 線分 $PQ$ の中点がセットされることになる。
5行目の IsLine(P, Q, R) は P、Q で指定される区間が線分であるかを調べるためのメソッドで、R が線分 $PQ$ の中点であればtrueを返す。
11行目以降は P、Q で指定される区間が弧となる場合であり(正確には弧と線分)、その場合には $PR$、$QR$ の長さに応じて以下の2つのケースに分かれる。
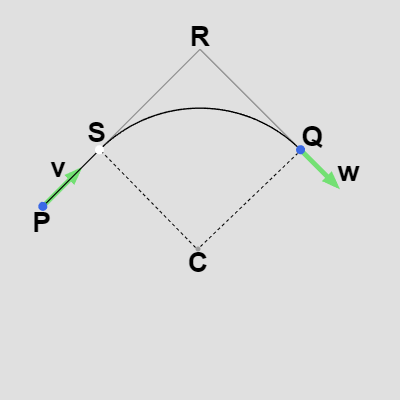
図5 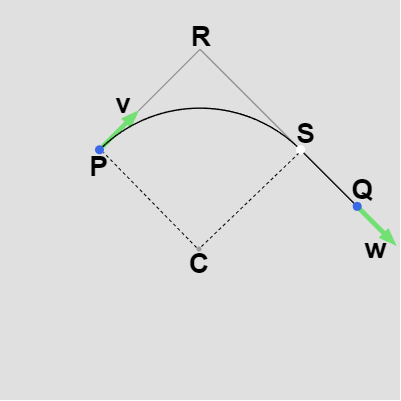
図6
$PR > QR$ (図5)であれば19行目のifブロック、$PR < QR$ (図6)ならば30行目のelseブロックである ($PR = QR$ の場合は図5のケースとして扱う)。
そして重要なのはその区間が線分であっても弧であっても、それぞれの箇所で List<Segment> 型引数 segments には segments.Add(new Segment(..)) として、各区間を表すSegmentが自動的に追加されていく。これによって自動的に補間曲線上のすべての区間がSegmentによって定義されることになるのである。
補間曲線上の全区間がSegmentによって定義され、各Segmentがある1つのList<Segment>型変数にセットされているとき(ここでもその変数名を segments とする)、補間曲線のために用意されたカスタムライブラリーのクラス BasicCurve を次のように用いることでこの補間曲線上の位置や接線の方向をパラメーター経由で取得することができるようになる。
BasicCurve クラスのコンストラクタの引数には補間曲線の各区間を表す全ての Segment を List<Segment> あるいは配列 Segment[] の形でセットする。このクラスには補間曲線上の位置や接線の方向を取得するために以下のメソッドが用意されている。
例えば上記の曲線の場合、曲線上の各地点を $0$ から $1$ の間の数値で表示すると下図7のようになる。図7の赤い数値は全体の長さを $1$ としたときの各地点までの距離を意味し、$P_1$ であればスタート地点($P_0$)から全体の長さの $26\%$ の位置にあり、$P_2$ であればスタート地点から $51\%$ の位置にあるということである。
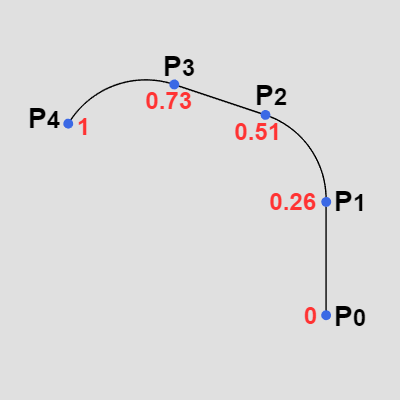
図7 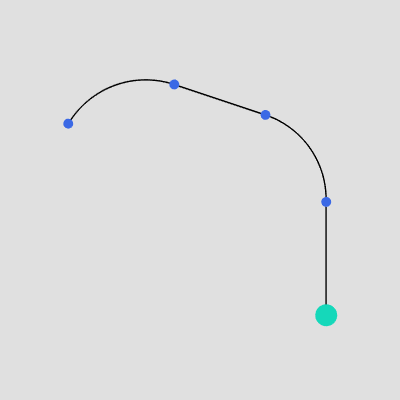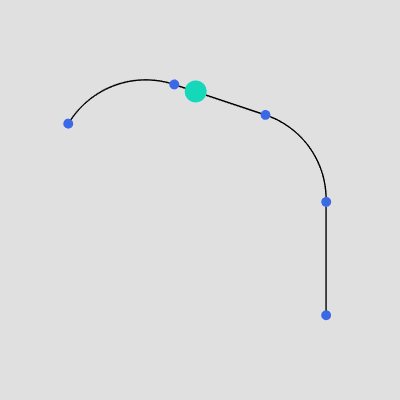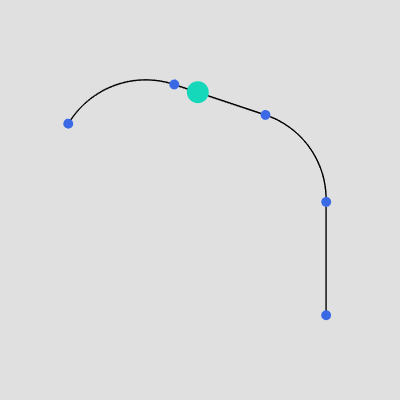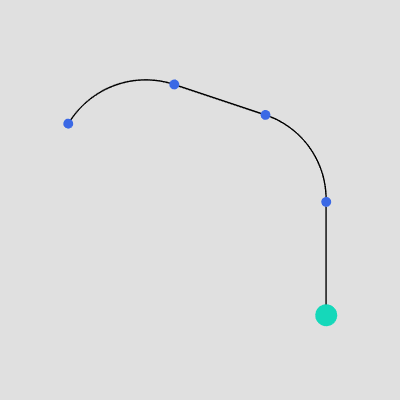
図8
そして図8に示されるように、プログラム中においてパラメーター t の値を $0$~$1$ の間で連続的に変化させることにより、オブジェクトを簡単に曲線上で移動させることができるようになるのである。
では実際のプログラムで見ていこう。
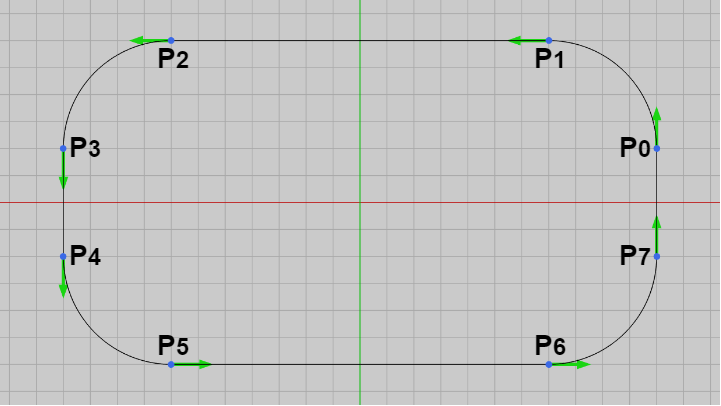
図9
使用するキー操作は以下のとおり。
J, K : Dotの移動 (K によって進み、J によって戻る)
プログラムを以下に示す。
[Code1] (実行結果 図9)
冒頭の GetPositionArray(..)、GetTangentArray(..) は各制御点の位置及び接線の方向を取得するためのメソッドで、戻り値はいずれもVector2[]の配列であり、今回は制御点の数は8個なので戻り値の要素数も8である。
初期化ブロックの内容は上の解説で述べたものであるが、今回使用している補間曲線が閉曲線であるため最初の制御点を最後の制御点としても使っている (10行目の i1 は最後のループにおいてその値が $0$ になる)。
26行目以降は2つのキー J、K によってDotを移動させる処理である。インスタンス変数 t の値は $0$~$1$ に変化するが、この t の値から補間曲線上の位置を計算し(35行目)、その位置へDotを移動させるだけである (実際にはこのプログラムでは t の値は $0$ を下回ったり、$1$ を上回ったりするが、ComputePosition(t) (35行目)の中でその値が自動的に $0$~$1$ の範囲に変換される)。
図10 Code1 実行結果
そして今回は簡単のためVehicleの現在位置における曲線上の接線の方向を、Vehicleの進行方向として定める。
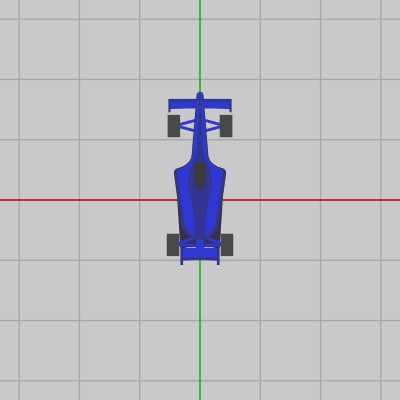
図11 Vehicle 初期状態 
図12 進行方向を向いた状態で移動
下図は今回使用する補間曲線であり、制御点の数は10個である。また今回も閉曲線であるため開始位置と終了位置は同じである (いずれも $P_0$ で進行方向は反時計周り。
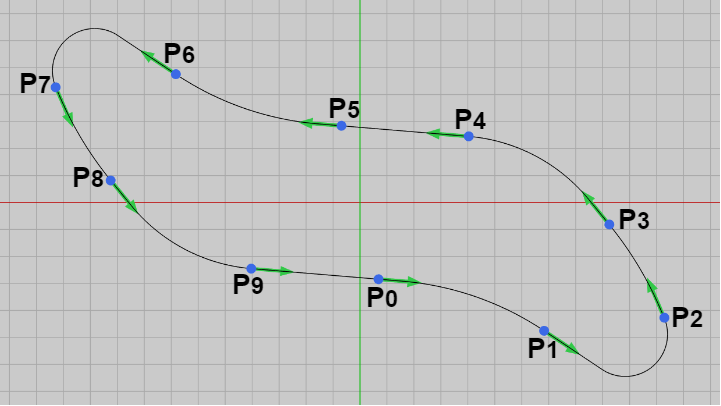
図13
しかし、実際にはVehicleの移動は以下のサーキット上において実装する (このサーキットのセンターラインは上図13の補間曲線と全く同じ形状である)。
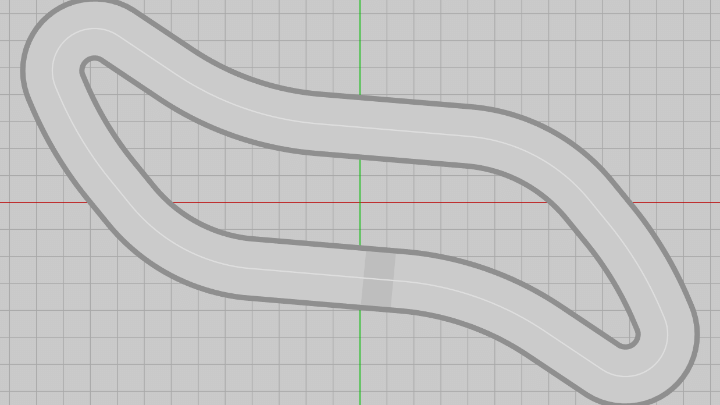
図14
プログラムを以下に示す。
[Code2] (実行結果 図15)
Code1との違いはVehicleには向きを指定する必要があるため、今回は毎フレーム ComputePositionAndTangent(t) (35行目)によって、t から計算される位置 pos とその位置における接線の方向 dir を取得している (戻り値には最初の要素に位置、次の要素に接線の方向がセットされる)。
Vehicleの進行方向は現在の位置における接線方向であるから、その方向へVehicleを向けるために適当な回転を実行する必要がある。40行目の CalcRotation3x3_V1toV2(..) はカスタムライブラリーのメソッドで、第1引数に指定されたベクトルの向きを第2引数に指定されたベクトルの向きと同じにするための回転を返すものである (第1引数のベクトル、第2引数のベクトルを $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ とすれば、このメソッドから取得される回転を $\boldsymbol{\mathsf{v_1}}$ に実行すると、 $\boldsymbol{\mathsf{v_1}}$ の向きは $\boldsymbol{\mathsf{v_2}}$ の向きと同じになる)。
プログラム中の dir は現在位置における接線の方向であるから、Vehicleを dir と同じ向きにすればよいわけである。CalcRotation3x3_V1toV2(..) の引数には Vector2.up と dir が指定されているが、これによって初期状態の向きから dir の方向へ向ける回転(R)が取得される。
したがって、Vehicleに実行される変換行列 T * R (41行目)の内容は、Vehicleを初期状態から dir の方向へ向け、その状態で pos に移動させるという順で行われる。これを毎フレーム繰り返すことによって、Vehicleは進行方向を向いた状態で曲線上(センターライン上)を移動していくことになる (図15)。
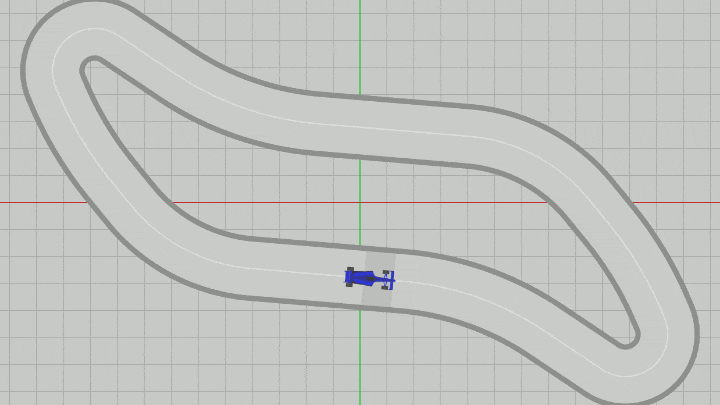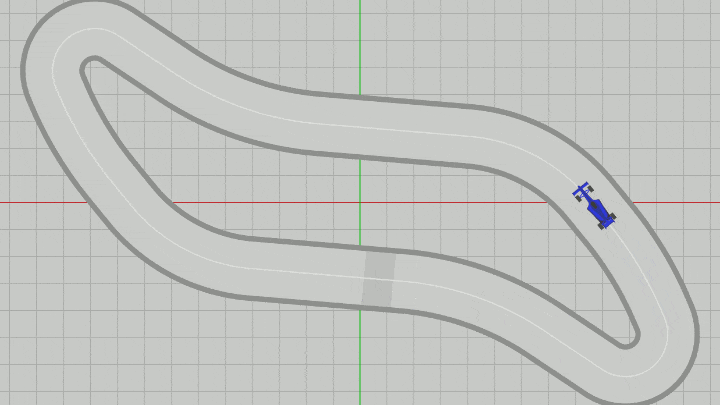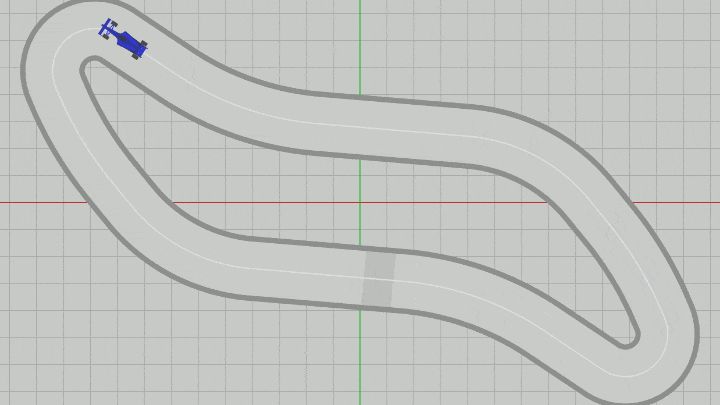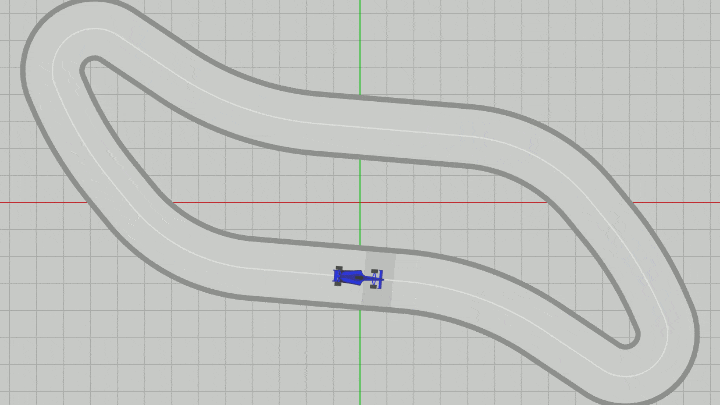
図15 Code2 実行結果

便宜上 $P_0$~$P_1$ の区間を 区間0、$P_1$~$P_2$ の区間を 区間1 のように表記する。
さらにここで区間を表すためのカスタムライブラリーのクラス Segment を用意する。Segment クラスは補間曲線を構成する各区間を表すクラスであり、区間が線分である場合と弧である場合によって使用するコンストラクタが異なる。
例えば右図の区間0は線分であり、具体的には線分 $P_0P_1$ であるが、区間が線分である場合にはコンストラクタの引数にその線分の両端の点を指定する。
// 区間が線分の場合のコンストラクタ var seg = new Segment(P0, P1);
区間1は弧であり、弧の両端の点は $P_1$、$P_2$、そして弧の中心(弧を含む円周の中心)は $C$ である。区間が弧である場合、コンストラクタにはその弧の両端の点及び弧の中心を指定する (引数の順序は2つの端点、弧の中心の順)。
// 区間が弧の場合のコンストラクタ var seg = new Segment(P1, P2, C);
上図の曲線は4つの区間によって構成されるが、この曲線をSegmentによって定義すると次のように記述される (ここでは各SegmentをListクラスにセットしている)。
List<Segment> segments = new List<Segment>()
{
new Segment(P0, P1), // 区間0 (線分)
new Segment(P1, P2, C), // 区間1 (弧)
new Segment(P2, P3), // 区間2 (線分)
new Segment(P3, P4, D) // 区間3 (弧)
}
曲線をSegmentによって定義する場合には必ず区間0、区間1、区間2、$...$ のように順番にセットしていく必要がある。Segment のコンストラクタにおいてもその最初の2つの引数には区間の両端点を指定するが、この両端点も曲線上での順序通りに指定しなければならない (例えば区間0の場合はコンストラクタの引数は $P_0$、$P_1$ の順であり、$P_1$、$P_0$ の順にはできない)。
前節における補間曲線は、実際にはいくつかの制御点とそれらの点における接線をもとにして作成された。例えば上図1の場合は下図2の制御点及び接線をもとに作成されている (図3は図2の制御点及び接線から構成された補間曲線であり、これは上図1のものと同じである)。


そして制御点及び接線による補間曲線の作成はプログラムでは次のように記述されていた (前節のものとは多少書き方を変えてある)。
Vector2[] arrP = GetPositionArray();
Vector2[] arrT = GetTangetnArray();
int numControl = arrP.Length;
for (int i = 0; i < numControl - 1; i++)
{
Vector2 P = arrP[i];
Vector2 v = arrT[i];
Vector2 Q = arrP[i + 1];
Vector2 w = arrT[i + 1];
Vector3 iR = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ(P, v, Q, w, iR);
}
このプログラムでは制御点は arrP[i]、それらの点における接線は arrT[i] であり、冒頭の GetPositionArray()、GetTangetnArray() は曲線を構成する制御点及び接線を取得するためのメソッドである。
前節においては上記13行目の InterpolatePQ(..) は補間曲線を作成するためのメソッドとして使われており、このメソッドの中で線分や弧の描画まで行われていた。しかし本節では補間曲線上の位置や接線の方向をパラメーターを介して取得することが目的であるため、補間曲線の描画自体は必要ではない。そのためこの InterpolatePQ(..) から余計な処理を削除して必要な処理だけを記述した InterpolatePQ_Data(..) というメソッドをここでは使うことにする。これによって上のプログラムは以下のように変更される。
Vector2[] arrP = GetPositionArray();
Vector2[] arrT = GetTangetnArray();
int numControl = arrP.Length;
List<Segment> segments = new List<Segment>()
for (int i = 0; i < numControl - 1; i++)
{
Vector2 P = arrP[i];
Vector2 v = arrT[i];
Vector2 Q = arrP[i + 1];
Vector2 w = arrT[i + 1];
Vector3 iR = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ_Data(P, v, Q, w, iR, segments);
}
InterpolatePQ_Data(..) (14行目)の最後の引数には List<Segment> 型の segments という変数が指定されているが、この segments には補間曲線をSegmentによって定義したときの各Segmentのデータがセットされる。
InterpolatePQ_Data(..) の具体的な内容を以下に示す。
void InterpolatePQ_Data(Vector2 P, Vector2 v, Vector2 Q, Vector2 w, Vector3 R3,
List<Segment> segments)
{
Vector2 R = R3;
if (R3.z < 0.0f || IsLine(P, Q, R))
{
segments.Add(new Segment(P, Q));
return;
}
float cosT = Vector2.Dot(-v, w);
float sinT = Mathf.Sqrt(1.0f - cosT * cosT);
float lenPR = (R - P).magnitude;
float lenQR = (R - Q).magnitude;
bool ccw = (-w.x * v.y + w.y * v.x > 0.0f) ? true : false;
Vector2 wr = ccw ? new Vector2(-w.y, w.x) : new Vector2(w.y, -w.x);
Vector2 S, C;
if (lenPR >= lenQR) // PR==QR==a (P==S) の場合を含む(この場合のLineは'点')
{
float a = lenQR;
float r = a * (1 - cosT) / sinT;
S = R - a * v;
C = Q + r * wr;
segments.Add(new Segment(P, S));
segments.Add(new Segment(S, Q, C));
}
else
{
float a = lenPR;
float r = a * (1 - cosT) / sinT;
S = R + a * w;
C = S + r * wr;
segments.Add(new Segment(P, S, C));
segments.Add(new Segment(S, Q));
}
}
冒頭のifブロック(5行目)は2つの隣り合う制御点 P、Q が線分区間となる場合である。引数 R3 には、P から v の方向に引いた直線と Q から w の方向に引いた直線の交点がセットされているが、2つの制御点及び接線が適切な位置関係にない場合にはこの R3 の z座標には $-1$ がセットされ、その場合には P と Q は線分で結ばれるのであった (前節参照)。

5行目の IsLine(P, Q, R) は P、Q で指定される区間が線分であるかを調べるためのメソッドで、R が線分 $PQ$ の中点であればtrueを返す。
11行目以降は P、Q で指定される区間が弧となる場合であり(正確には弧と線分)、その場合には $PR$、$QR$ の長さに応じて以下の2つのケースに分かれる。


$PR > QR$ (図5)であれば19行目のifブロック、$PR < QR$ (図6)ならば30行目のelseブロックである ($PR = QR$ の場合は図5のケースとして扱う)。
そして重要なのはその区間が線分であっても弧であっても、それぞれの箇所で List<Segment> 型引数 segments には segments.Add(new Segment(..)) として、各区間を表すSegmentが自動的に追加されていく。これによって自動的に補間曲線上のすべての区間がSegmentによって定義されることになるのである。
補間曲線上の全区間がSegmentによって定義され、各Segmentがある1つのList<Segment>型変数にセットされているとき(ここでもその変数名を segments とする)、補間曲線のために用意されたカスタムライブラリーのクラス BasicCurve を次のように用いることでこの補間曲線上の位置や接線の方向をパラメーター経由で取得することができるようになる。
BasicCurve curve = new BasicCurve(segments); float t = 0.5f; Vector2 pos = curve.ComputePosition(t); Vector2[] vrr = curve.ComputePositionAndTangent(t);
BasicCurve クラスのコンストラクタの引数には補間曲線の各区間を表す全ての Segment を List<Segment> あるいは配列 Segment[] の形でセットする。このクラスには補間曲線上の位置や接線の方向を取得するために以下のメソッドが用意されている。
ComputePosition(t)
: 引数に指定されたfloat型パラメーター t の値から曲線上の位置を返す (戻り値は Vector2 ; パラメーター t は $0$~$1$ の間でなければならない)。ComputePositionAndTangent(t)
: 引数に指定されたfloat型パラメーター t の値から曲線上の位置及び接線の方向を返す (戻り値は配列 Vector2[] ; パラメーター t は $0$~$1$ の間でなければならない)。例えば上記の曲線の場合、曲線上の各地点を $0$ から $1$ の間の数値で表示すると下図7のようになる。図7の赤い数値は全体の長さを $1$ としたときの各地点までの距離を意味し、$P_1$ であればスタート地点($P_0$)から全体の長さの $26\%$ の位置にあり、$P_2$ であればスタート地点から $51\%$ の位置にあるということである。


そして図8に示されるように、プログラム中においてパラメーター t の値を $0$~$1$ の間で連続的に変化させることにより、オブジェクトを簡単に曲線上で移動させることができるようになるのである。
では実際のプログラムで見ていこう。
# Code1
最初のプログラムでは小さい円形オブジェクト Dot を、以下のトラック型の曲線上で移動させる。このトラック型の曲線は制御点8個で構成され、閉曲線であるため開始位置と終了位置が同じである (いずれも $P_0$ で進行方向は反時計周り)。
使用するキー操作は以下のとおり。
J, K : Dotの移動 (K によって進み、J によって戻る)
プログラムを以下に示す。
[Code1] (実行結果 図9)
if (!i_INITIALIZED)
{
Vector2[] arrP = GetPositionArray(1);
Vector2[] arrT = GetTangentArray(1);
List<Segment> segments = new List<Segment>();
int numControl = arrP.Length;
for (int i = 0; i < numControl; i++)
{
int i1 = (i + 1) % numControl;
Vector2 P = arrP[i];
Vector2 v = arrT[i];
Vector2 Q = arrP[i1];
Vector2 w = arrT[i1];
Vector3 iR = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ_Data(P, v, Q, w, iR, segments);
}
Curve = new BasicCurve(segments);
t = 0.0f;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.K))
{
t += 0.002f;
}
else if (Input.GetKey(KeyCode.J))
{
t -= 0.002f;
}
Vector2 pos = Curve.ComputePosition(t);
Dot.SetPosition(pos);
冒頭の GetPositionArray(..)、GetTangentArray(..) は各制御点の位置及び接線の方向を取得するためのメソッドで、戻り値はいずれもVector2[]の配列であり、今回は制御点の数は8個なので戻り値の要素数も8である。
初期化ブロックの内容は上の解説で述べたものであるが、今回使用している補間曲線が閉曲線であるため最初の制御点を最後の制御点としても使っている (10行目の i1 は最後のループにおいてその値が $0$ になる)。
26行目以降は2つのキー J、K によってDotを移動させる処理である。インスタンス変数 t の値は $0$~$1$ に変化するが、この t の値から補間曲線上の位置を計算し(35行目)、その位置へDotを移動させるだけである (実際にはこのプログラムでは t の値は $0$ を下回ったり、$1$ を上回ったりするが、ComputePosition(t) (35行目)の中でその値が自動的に $0$~$1$ の範囲に変換される)。

# Code2
では続いて補間曲線上の移動を行うオブジェクトとして以下の Vehicle を使用する。Vehicleは上記のDotとは異なり向きがあり、初期状態においては y軸プラス方向を向いている (図11)。そのため曲線上を移動する際には、図12に示されるように進行方向を向いた状態で移動していくようにする必要がある。そして今回は簡単のためVehicleの現在位置における曲線上の接線の方向を、Vehicleの進行方向として定める。


下図は今回使用する補間曲線であり、制御点の数は10個である。また今回も閉曲線であるため開始位置と終了位置は同じである (いずれも $P_0$ で進行方向は反時計周り。

しかし、実際にはVehicleの移動は以下のサーキット上において実装する (このサーキットのセンターラインは上図13の補間曲線と全く同じ形状である)。

プログラムを以下に示す。
[Code2] (実行結果 図15)
if (!i_INITIALIZED)
{
Vector2[] arrP = GetPositionArray(2);
Vector2[] arrT = GetTangentArray(2);
List<Segment> segments = new List<Segment>();
int numControl = arrP.Length;
for (int i = 0; i < numControl; i++)
{
int i1 = (i + 1) % numControl;
Vector2 P = arrP[i];
Vector2 v = arrT[i];
Vector2 Q = arrP[i1];
Vector2 w = arrT[i1];
Vector3 iR = CalcIntersectionOf2Lines(P, v, Q, w);
InterpolatePQ_Data(P, v, Q, w, iR, segments);
}
Curve = new BasicCurve(segments);
t = 0.0f;
i_INITIALIZED = true;
}
if (Input.GetKey(KeyCode.K))
{
t += 0.0025f;
}
else if (Input.GetKey(KeyCode.J))
{
t -= 0.0025f;
}
Vector2[] vrr = Curve.ComputePositionAndTangent(t);
Vector2 pos = vrr[0];
Vector2 dir = vrr[1];
THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos);
THMatrix3x3 R = TH2DMath.CalcRotation3x3_V1toV2(Vector2.up, dir);
Vehicle.SetMatrix(T * R);
Code1との違いはVehicleには向きを指定する必要があるため、今回は毎フレーム ComputePositionAndTangent(t) (35行目)によって、t から計算される位置 pos とその位置における接線の方向 dir を取得している (戻り値には最初の要素に位置、次の要素に接線の方向がセットされる)。
Vehicleの進行方向は現在の位置における接線方向であるから、その方向へVehicleを向けるために適当な回転を実行する必要がある。40行目の CalcRotation3x3_V1toV2(..) はカスタムライブラリーのメソッドで、第1引数に指定されたベクトルの向きを第2引数に指定されたベクトルの向きと同じにするための回転を返すものである (第1引数のベクトル、第2引数のベクトルを $\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ とすれば、このメソッドから取得される回転を $\boldsymbol{\mathsf{v_1}}$ に実行すると、 $\boldsymbol{\mathsf{v_1}}$ の向きは $\boldsymbol{\mathsf{v_2}}$ の向きと同じになる)。
プログラム中の dir は現在位置における接線の方向であるから、Vehicleを dir と同じ向きにすればよいわけである。CalcRotation3x3_V1toV2(..) の引数には Vector2.up と dir が指定されているが、これによって初期状態の向きから dir の方向へ向ける回転(R)が取得される。
したがって、Vehicleに実行される変換行列 T * R (41行目)の内容は、Vehicleを初期状態から dir の方向へ向け、その状態で pos に移動させるという順で行われる。これを毎フレーム繰り返すことによって、Vehicleは進行方向を向いた状態で曲線上(センターライン上)を移動していくことになる (図15)。

© 2020-2025 Redpoll's 60 (All rights reserved)