Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-24
第2章 2D空間におけるオブジェクトの運動
$§$2-24 衝突判定 11 (直線 vs 長方形、円盤、直線)
本節では直線に関連した衝突判定について見ていく。具体的には直線と長方形、直線と円盤、及び直線同士の衝突判定である。
図1は横の長さ $w$、縦の長さ $h$ の長方形であり、各辺は x軸、y軸に平行、その中心は原点に置かれている。
この長方形を縦方向に無限に伸ばした領域を「X領域」、横方向に無限に伸ばした領域を「Y領域」と呼ぶことにする。X領域はその横の長さが $w$ でその領域を x軸が貫いており、Y領域はその縦の長さが $h$ でその領域を y軸が貫いている。図から明らかなように長方形はこの2つの領域、X領域、Y領域の交差部分に等しい。
また XY平面上の点 $R_0$ から半直線を引き、その方向を $\boldsymbol{\mathsf{v}}$ とする (図5)。ここではこの半直線のことをレイ(Ray)と呼ぶことにする。
$\boldsymbol{\mathsf{v}}$ は方向を表すベクトルであるが、以下の解説においては $\boldsymbol{\mathsf{v}}$ を大きさ(速さ) $1$ の速度ベクトルとして扱う。すなわち 図5のレイ(半直線)は矢印の方向に速さ $1$ で進んでいくものとして考える。
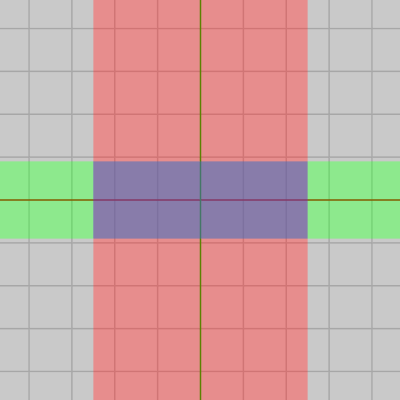
図4 長方形はX領域とY領域の交差部分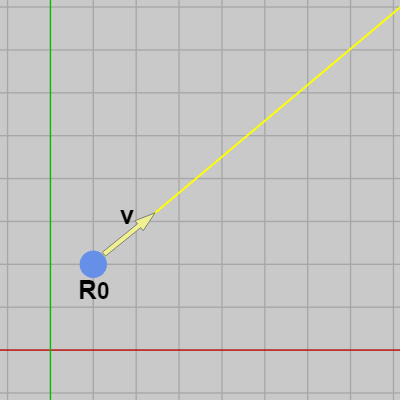 
図5 レイ (始点 R0、方向 v の半直線)
今 この半直線と長方形が衝突したとしよう (図6)。
下図7に示されるようにこのときレイは長方形のX領域、Y領域の交差部分を通過する。
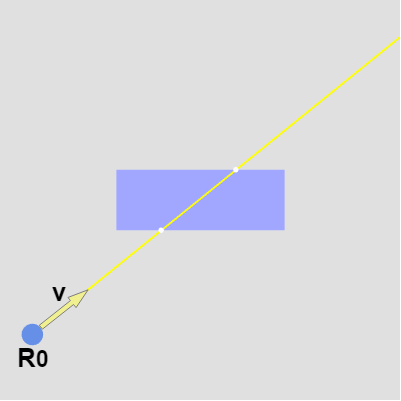
図6 レイと長方形の衝突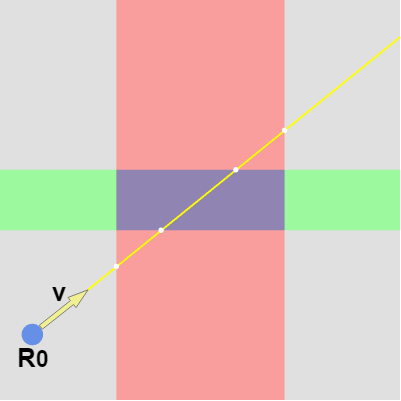 
図7 レイはX領域、Y領域の交差部分を通過する
レイが始点 $R_0$ を出発してからX領域に入るまでにかかる時間(X領域と最初に衝突するまでにかかる時間)を $inX$ とし、$R_0$ を出発してからX領域を出るまでにかかる時間(X領域と2回目に衝突するまでにかかる時間)を $outX$ とする (図8)。
同様に レイが $R_0$ を出発してからY領域に入るまでにかかる時間を $inY$、$R_0$ を出発してからY領域を出るまでにかかる時間にかかる時間を $outY$ とする。
($inX$、$outX$、$inY$、$outY$ は経過時間である。距離や位置ではないことに注意)
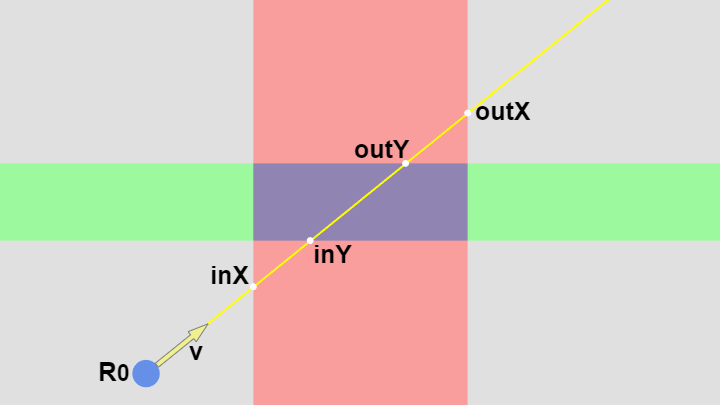
図8 inX, outX, inY, outY は経過時間を表す
上図の場合、レイは始点 $R_0$ を出発してからまず X領域に入り、次にY領域に入る。その後 Y領域を出てから最後にX領域を出る。上で述べたように長方形はX領域、Y領域の交差部分であるから、レイが長方形の中を進んでいる間はX領域、Y領域の両方にいることになる。
レイがX領域にいるのは $inX$~$outX$ の間であり、レイがY領域にいるのは $inY$~$outY$ の間である。したがって、レイが長方形の中を進む場合(それはレイが長方形と衝突することを意味する)はこの2つの区間 $inX$~$outX$、$inY$~$outY$ に重なりがあるということである。
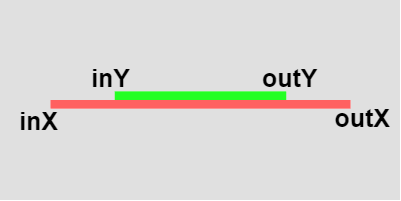
図9 2つの区間には重なりがある (inY~outYにおいて重なっている) 実際、図8の場合は経過時間の大小関係は $inX < inY < outY < outX$ なので右図に示されるように2つの区間には $inY$~$outY$ において重なりがある。
2-19節で見たように2つの区間 $inX$~$outX$、$inY$~$outY$ の間に重なりがあるかどうかは以下の条件式を調べればよい。
\[ inX < outY\ \ \&\&\ \ inY < outX \]今回の例でいえばこの条件式が成り立つならばレイと長方形は衝突するということである (2つの区間の重なりの部分は、レイが長方形の中を進んでいる時間に相当する。図9の場合は2つの区間の重なりは $inY$~$outY$ であるが、この区間においてレイは長方形の中を進んでいる)。
下図はレイと長方形が衝突する別のケースである。経過時間の大小関係は $inY < inX < outY < outX$ であり、2つの区間 $inX$~$outX$、$inY$~$outY$ は $inX$~$outY$ において重なっているが、図に示されるようにこの区間においてレイは長方形の中を進んでいる。
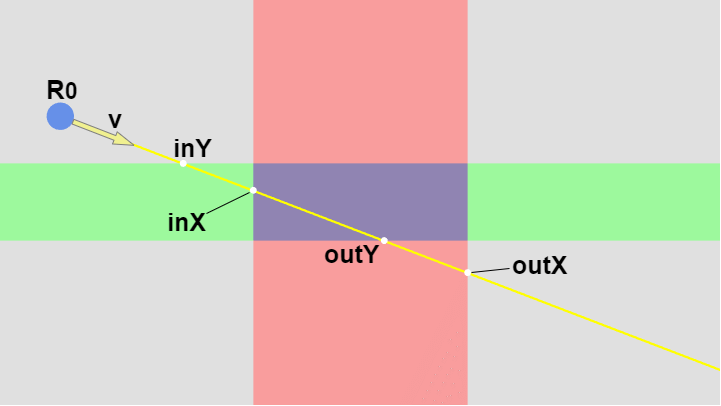
図10 inX~outYの間にレイは長方形を通過する
以下の2つの図はレイと長方形が衝突していないケースであるが、いずれの場合にも上記の重なり判定の条件式が成立していないことがわかるであろう (左図の場合は $inX > outY$ であり、右図の場合は $inY > outX$ になっている)。
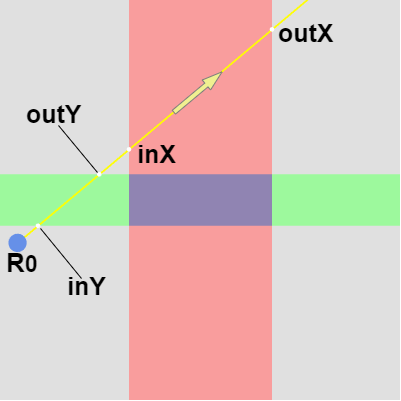
図11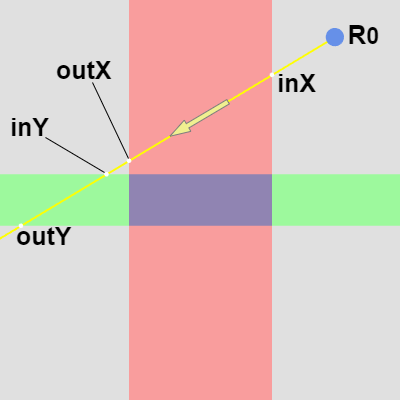 
図12
レイと長方形との衝突判定ではレイがある領域に入る前に、別の領域から出てしまうようなことがあれば両者が衝突することはない。上図11の場合はレイがX領域に入る前にY領域を出てしまっており、図12の場合はレイがY領域に入る前にX領域を出てしまっている。
レイと長方形が衝突する場合とは、レイがX領域を進んでいる間にY領域に入る、あるいはレイがY領域を進んでいる間にX領域に入る場合のいずれかである。そしてその場合にはレイが(最初の領域ではなく)第2の領域に入る時点で長方形との衝突が発生する。
例えば レイがY領域を進んでいる間にX領域に入る場合には、レイが出発してから $inX$ 経過した時点でレイと長方形が衝突することになる (上図10の衝突はこのケースである)。
図13 左下隅の頂点が (xmin, ymin)、 右上隅の頂点が (xmax, ymax) 以下では長方形の左下隅の頂点を $(xmin,\ ymin)$、右上隅の頂点を $(xmax,\ ymax)$ と表記する (図13)。
(使われる変数が増えてきたが、$inX$、$outX$、$inY$、$outY$ は経過時間であり、$(xmin,\ ymin)$、$(xmax,\ ymax)$ は長方形の頂点座標である)
$inX$ や $outX$ を求めるには次のように考えればよい。
上で定めたことに従えばレイが始点 $R_0$ を速度 $\boldsymbol{\mathsf{v}}$ で出発してからX領域に(最初に)衝突するまでにかかる時間が $inX$ であるが、このときのレイとX領域との衝突点を $P$ とする (図14)。また、速度ベクトル $\boldsymbol{\mathsf{v}}$ の x成分を $\boldsymbol{\mathsf{v}}.x$、y成分を $\boldsymbol{\mathsf{v}}.y$ とする。
速度ベクトル $\boldsymbol{\mathsf{v}}$ は単位ベクトルであるからその大きさ(速さ)は $1$ である。したがって、レイが $R_0$ を出発して、$\boldsymbol{\mathsf{v}}$ の方向に速さ $1$ で進むとき、時間 $inX$ 後に点 $P$ に衝突するわけであるが、この同じ時間の間に $\boldsymbol{\mathsf{v}}$ の x成分 $\boldsymbol{\mathsf{v}}.x$ は $R_0$ から図14の $P'$ まで進むことになる。
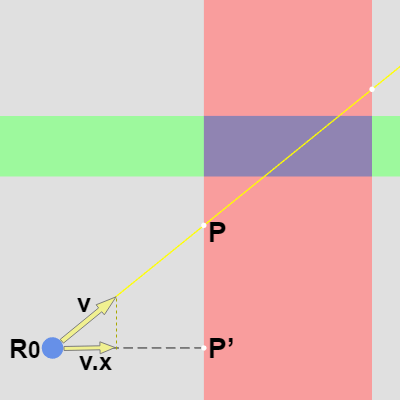
図14 速度ベクトル v がR0からPまで進むのにかかる時間は inX であるが、同じ時間に v の x成分 v.x はR0からP’まで進む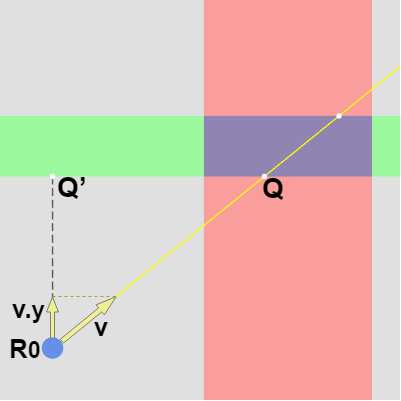 
図15 速度ベクトル v がR0からQまで進むのにかかる時間は inY であるが、同じ時間に v の y成分 v.y はR0からQ’まで進む
$R_0$ から $P'$ に進む際には y軸方向の移動がないので、その距離は $P'\!.x - R_0.x$ であり、$P'\!.x = xmin$ であるため、結局\[ (xmin - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = inX \]となり、$outX$ は\[ (xmax - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = outX \]として求められる。
$inY$、$outY$ の求め方も同様である。ここではレイとY領域の最初の衝突点を $Q$ とする (図15)。この場合 レイが $R_0$ を出発して、$\boldsymbol{\mathsf{v}}$ の方向に速さ $1$ で進むとき、時間 $inY$ 後に点 $Q$ に衝突するわけであるが、この同じ時間の間に $\boldsymbol{\mathsf{v}}$ の y成分 $\boldsymbol{\mathsf{v}}.y$ は $R_0$ から図15の $Q'$ まで進むことになる。
$R_0$ から $Q'$ に進む際には x軸方向の移動がないので、その距離は $Q'\!.y - R_0.y$ であり、$Q'\!.y = ymin$ であるため、結局\begin{align*}(ymin - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = inY \\\\(ymax - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = outY \end{align*}となる。
上の例では長方形の左下隅の座標を $(xmin,\ ymin)$、右上隅の座標を $(xmax,\ ymax)$ としたとき、$inX$ や $inY$ を求める際には $xmin$ や $ymin$ が使われ、$outX$ や $outY$ を求める際には $xmax$ や $ymax$ が使われた。しかし、一般には必ずしもこれは当てはまらない。
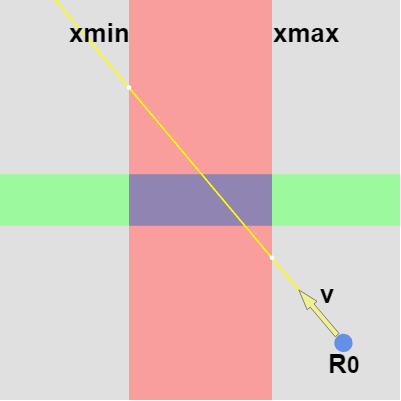
図16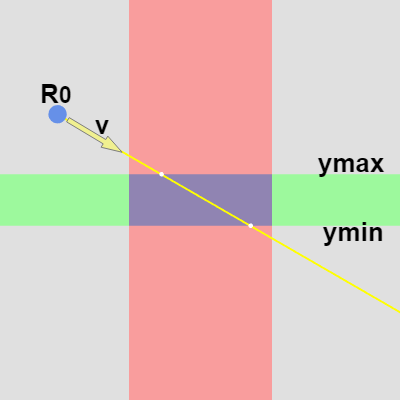 
図17
例えば、レイの始点 $R_0$ 及びその方向 $\boldsymbol{\mathsf{v}}$ が上左図の場合には $inX$、$outX$ は\begin{align*}(xmax - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = inX \\\\(xmin - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = outX \end{align*}となるし、$R_0$、$\boldsymbol{\mathsf{v}}$ が上右図の場合には $inY$、$outY$ は\begin{align*}(ymax - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = inY \\\\(ymin - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = outY \end{align*}となる。つまり レイと長方形の相対的な位置関係によって $inX$、$inY$、$outX$、$outY$ の求め方は変わってくるのである。
しかし、それらの値を求める際には場合分けをすることなく簡単に求めることができる。例えば $inX$、$outX$ の場合であれば、上図14の場合のように $inX$ は $xmin$ を使って計算し、$outX$ は $xmax$ を使って計算する。そして、$inX$ が $outX$ よりも大きい場合には両者を入れ替えればよい。それだけである。
上の例における長方形はその各辺が x軸、y軸に平行、すなわち 軸平行な長方形であった。以下では長方形が軸平行でない場合、すなわち 長方形が回転している場合について考える (以下の内容は 2-20節と実質的には同じである)。
各辺の長さが $w$、$h$ の長方形とレイが下図18に示される状態で置かれている。図中の $T$ は長方形の中心である。
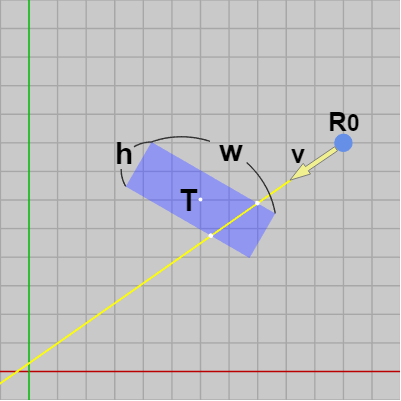
図18 傾きのある長方形とレイの衝突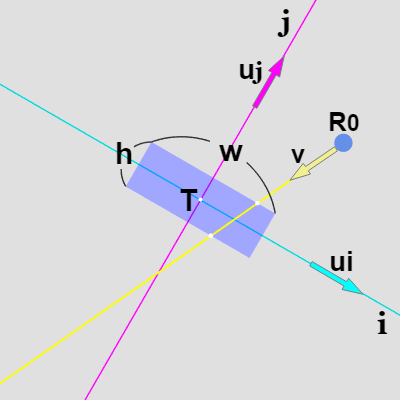 
図19 Tを原点とする ij 座標系
$T$ を通り長方形の長い辺に平行な直線を i 軸、同じく $T$ を通り長方形の短い辺に平行な直線を j 軸とする。また i 軸、j 軸の方向を表す単位ベクトルを $\boldsymbol{u_i}$、$\boldsymbol{u_j}$ とする (図19 ; 以下ではこの $T$ を原点とする座標系を簡単に ij 座標系と呼ぶことにする)。
この ij 座標系におけるレイの始点 $R_0$、及びその方向 $\boldsymbol{\mathsf{v}}$ を求めよう。
上記では $R_0$ の x座標、y座標を $R_0.\!x$、$R_0.\!y$ として用いたが、この $R_0.\!x$、$R_0.\!y$ は詳しくは始点 $R_0$ が xy座標系の原点から x軸方向に $R_0.\!x$、y軸方向に $R_0.\!y$ だけ離れていることを意味する (図20)。
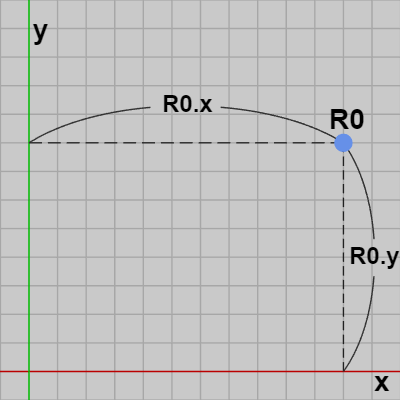
図20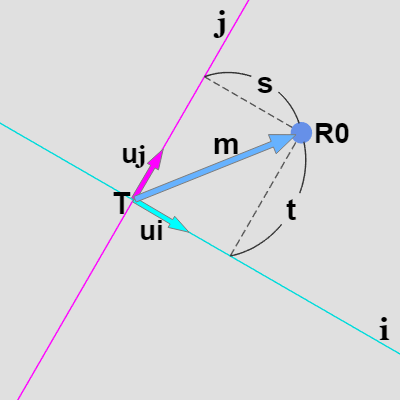 
図21 R0は ij 座標系において、原点 T から i 軸方向に s、j 軸方向に t だけ離れている
したがって $R_0$ の ij 座標系での値を求めるには、$R_0$ が ij 座標系の原点 $T$ から i 軸方向、j 軸方向にどれだけ離れているかを調べる必要がある。ここではそれらの距離を $s$、$t$ とする (図21)。
$T$ と $R_0$ を結ぶベクトルを $\boldsymbol{m}\ (= R_0 - T)$ とすれば、i 軸方向の距離 $s$、j 軸方向の距離 $t$ は次のように求められる。
\begin{align*} \boldsymbol{m} \cdot \boldsymbol{u_i} = s \\\\ \boldsymbol{m} \cdot \boldsymbol{u_j} = t\end{align*}つまり $R_0$ の ij 座標系における座標は $(\boldsymbol{m} \cdot \boldsymbol{u_i},\ \boldsymbol{m} \cdot \boldsymbol{u_j})$ である。
レイの方向 $\boldsymbol{\mathsf{v}}$ の ij 座標系での値を求める場合も同様の手順で進めればよい。上記と同じく $\boldsymbol{\mathsf{v}}$ の x座標、y座標を $\boldsymbol{\mathsf{v}}.x$、$\boldsymbol{\mathsf{v}}.y$ とすれば、これらの値が意味することは xy座標系において $\boldsymbol{\mathsf{v}}$ の始点から終点までの距離は、x軸方向に $\boldsymbol{\mathsf{v}}.x$、y軸方向に $\boldsymbol{\mathsf{v}}.y$ だけ離れているということである。(図22はわかりやすくするために $\boldsymbol{\mathsf{v}}$ の始点を xy座標系の原点に置いたときのものである。この図における $\boldsymbol{\mathsf{v}}.x$、$\boldsymbol{\mathsf{v}}.y$ の値はいずれもマイナスである)。
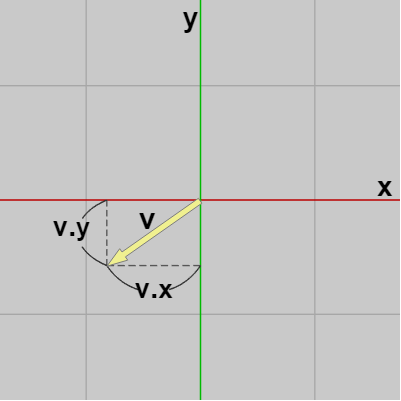
図22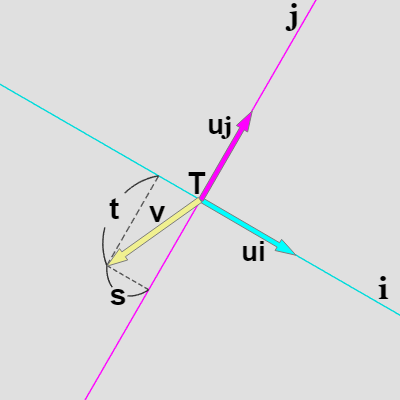 
図23 v の終点は ij 座標系において、原点 T から i 軸方向に s、j 軸方向に t だけ離れている (この図では s、t ともにマイナス値)
$\boldsymbol{\mathsf{v}}$ の ij 座標系での値を求めるには、$\boldsymbol{\mathsf{v}}$ の始点を ij 座標系の原点 $T$ に置いたときに、$\boldsymbol{\mathsf{v}}$ の終点が $T$ から i 軸方向、j 軸方向にどれだけ離れているかを計算すればよい。
それらの距離をここでも $s$、$t$ とすれば (図23)、\begin{align*} \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i} = s \\\\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j} = t\end{align*}となる。つまり $\boldsymbol{\mathsf{v}}$ の ij 座標系における値は $(\boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i},\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j})$ である (これはすなわち $\boldsymbol{\mathsf{v}}$ の ij 座標系における方向である)。
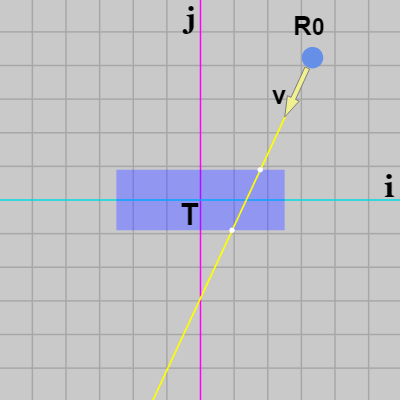
図24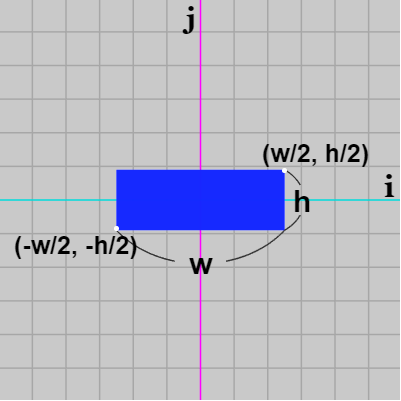 
図25
$R_0$、$\boldsymbol{\mathsf{v}}$ の ij 座標系での値がわかれば、あとは i 軸、j 軸に平行な長方形とレイとの衝突を考えることと同じである (図24)。そしてこの場合には長方形の中心 $T$ は ij 座標系の原点でもあるので、各辺の長さを $w$、$h$ とすれば長方形の左下隅の頂点 $(xmin,\ ymin)$ の値は $(-w/2, -h/2)$ であり、右上隅の頂点 $(xmax,\ ymax)$ の値は $(w/2,\ h/2)$ である (図25)。
ij 座標系においてレイと長方形の衝突点を求めた後はその衝突点の座標を xy座標系での値に変換しなければならない。始点 $R_0$ から出発したレイが長方形と衝突するまでにかかる時間は ij 座標系において測っても、xy座標系において測っても同じである (ここでは $|\boldsymbol{\mathsf{v}|=1}$ なので時間ではなく距離と考えてもよい。すなわち衝突点までの距離は ij 座標系で測っても xy座標系で測っても同じである)。
したがって ij 座標系においては実際には衝突点を計算する必要はなく、衝突までにかかる時間がわかればよい。ここでは長方形に最初に衝突するまでにかかる時間を $k_0$、長方形に2回目に衝突する(長方形から出ていくとき)までにかかる時間を $k_1$ とする。そのとき衝突点は簡単に\[ R_0 + k_0 \boldsymbol{\mathsf{v}} = P_0 \qquad\qquad R_0 + k_1 \boldsymbol{\mathsf{v}} = P_1\]として求められる ($P_0$ が最初の衝突点)。
次のメソッド CollisionTest_Ray_AABB(..) はレイと軸平行な長方形との衝突判定メソッドであり、上で述べてきたことを実装したものである。
[CollisionTest_Ray_AABB(..)]
第1引数 R0 はレイの始点、第2引数 v はレイの方向を表す単位ベクトル、第3引数 min_max は長方形の左下隅、右上隅の頂点(上図13)がセットされた配列である (Vector2[]型)。
プログラム中で使われている各変数 xmin、ymin、inX、outX などは上の解説のものと意味は同じである。
11~23行目はレイの始点 R0 からX領域に衝突するまでの経過時間 inX、X領域から出るまでの経過時間 outX の計算であり、26~38行目は R0 からY領域に衝突するまでの経過時間 inY、Y領域から出るまでの経過時間 outY の計算である。
どちらも if/else ブロックで記述されているが、if ブロックはレイの方向 v が x軸あるいは y軸に平行な場合、else ブロックの方は v が x軸にも y軸にも平行でない場合であり、else ブロック内の計算は上の解説で述べた通りである。THUtil.Swap(ref a, ref b) はカスタムライブラリーのメソッドで、第1引数の値と第2引数の値を入れ替えるためのものであり、inX が outX よりも小さい値になるように、inY が outY よりも小さい値になるようにするために使用している。
v が x軸あるいは y軸に平行な場合については後に回すとして、先に40行目以降を見ていく。
41行目の判定はレイと長方形が衝突しているかを調べるものであり、\[ inX < outY\ \ \&\&\ \ inY < outX \]が成り立つ場合には両者が衝突している。
ただしレイと長方形が衝突していても衝突点がレイの始点 R0 から後ろの方向(v を基準にして後ろ)にある場合には、衝突とはみなさずに衝突していないものとして null を返す (43行目 ; この場合には inX、inY ともにマイナスになる)。
衝突している場合にはレイと長方形の衝突点は2つある (1つの場合も重複しているものとして考える)。1つはレイの始点から近い方の衝突点であり、もう1つは遠い方の衝突点である。このメソッドではその2つの衝突点を配列として返すが最初の要素に近い方の衝突点、2番目の要素に遠い方の衝突点をセットする (48行目)。
最後にレイの方向 v が x軸あるいは y軸に平行である場合について見ていこう。上の解説ではレイの方向 v は x軸にも y軸にも平行でないことを前提としていたが、もし v が x軸あるいは y軸に平行である場合は特別な処理が必要になる (11、26行目の if ブロック)。
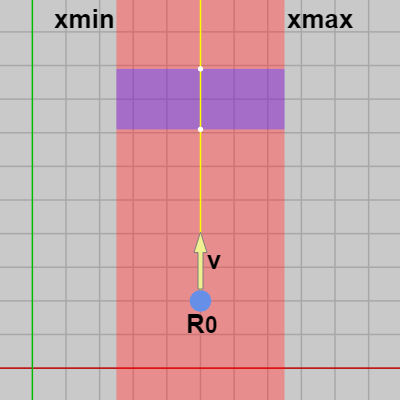
図27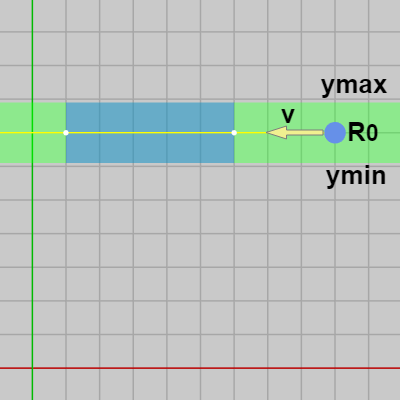 
図28
例えば v が y軸に平行( v.x==0 )であるとしよう。この場合には図27に示されるようにレイの始点 R0 がX領域に含まれていなければ衝突することはないので、この時点で衝突していないことを示す null を返す (13行目)。X領域に含まれている場合でもレイと長方形は衝突するが、レイとX領域は衝突することはない。そのため inX、outX には特別に NegativeInfinity、PositiveInfinity をセットしている (15、16行目)。
v が x軸に平行( v.y==0 )も同様である (図28)。この場合には R0 がY領域に含まれていなければ衝突することはないので null を返し(28行目)、Y領域に含まれている場合は inY、outY には NegativeInfinity、PositiveInfinity をセットする (30、31行目)。
次のメソッド CollisitonTest_Ray_Rect(..) はレイと長方形との衝突判定メソッドであり、このメソッドでは傾きのある長方形も対象とする。
[CollisitonTest_Ray_Rect(..)]
図19 最初の2つの引数はここでもレイの始点 R0 とレイの方向 v である (ここでは v は単位ベクトルでなくても構わない)。第3引数以降は長方形に関するデータであり、中心 $T$、各辺の方向を表す単位ベクトル ui、uj、各辺の長さ w、h をセットする。
4~7行目までが ij 座標系での R0 の値の計算、9~11行目までが ij 座標系での v の値の計算であり、それぞれ locR0、locV というローカル変数にセットされる。
そして先程述べたように ij 座標系で衝突判定を行う場合は長方形の中心 T は原点に位置し、長方形の各辺は i 軸、j 軸に平行であるので衝突判定は、ij 座標系においてレイと軸平行な長方形の衝突判定を行うことと同じである。その際に使用する長方形の左下隅、右上隅の頂点は長方形の各辺の長さが w、h であるとき、(-w/2, -h/2)、(w/2, h/2) となる (13~15行目)。
15行目の ComputeT_Ray_AABB(..) はレイと長方形が衝突するまでにかかる時間を計算するメソッドであり、これは ij 座標系における計算である。衝突した場合には ti に2つのfloat値がセットされるが、これは上で述べた最初の衝突までにかかる時間、2回目の衝突までにかかる時間である。すなわち ti[0]、ti[1] は先ほどの $k_0$、$k_1$ のことであり、18行目の計算は以下の計算に相当する。
\[ R_0 + k_0 \boldsymbol{\mathsf{v}} = P_0 \qquad\qquad R_0 + k_1 \boldsymbol{\mathsf{v}} = P_1\]
上記の CollisionTest_Ray_AABB(..) と内容自体は同じである。
[ComputeT_Ray_AABB(..)]
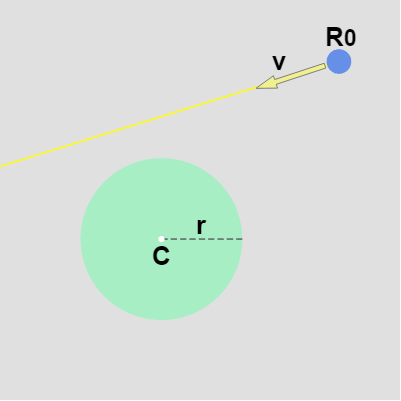
図29 円盤とレイ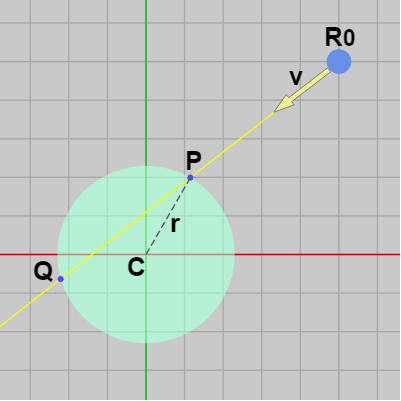 
図30
簡単のため円盤の中心 $C$ が原点に置かれている場合で進める。
またここではレイが始点 $R_0$ を出発してから円盤との最初の衝突点を $P$、第2の衝突点を $Q$ とする (図30)。レイが $R_0$ を速度 $\boldsymbol{\mathsf{v}}$ で出発して点 $P$ に衝突するまでにかかる時間を $t$ とすれば\[ R_0 + t\boldsymbol{\mathsf{v}} = P \]である。
$P$ は、中心 $C$、半径 $r$ の円周上の点であり、ここでは $C$ は原点に置かれているから\[|P - C| = |P - O| = |P| = r\]である (式中の $O$ は原点)。
すなわち $|R_0 + t\boldsymbol{\mathsf{v}}| = r\ (= |P|)\ $ であり、この両辺を2乗すると\[|R_0 + t\boldsymbol{\mathsf{v}}|^2 = r^2\]である。
したがって、\begin{align*}&|R_0 + t\boldsymbol{\mathsf{v}}|^2 - r^2 \\\\=\ &(R_0 + t\boldsymbol{\mathsf{v}})\cdot(R_0 + t\boldsymbol{\mathsf{v}}) - r^2 \\\\=\ &|\boldsymbol{\mathsf{v}}|^2t^2 + 2(R_0\cdot \boldsymbol{\mathsf{v}})t + (|R_0|^2 - r^2) \\\\=\ &0\end{align*}と展開される (ベクトルの内積に関しては分配法則、すなわち $\boldsymbol{a} \cdot (\boldsymbol{b} + \boldsymbol{c}) = \boldsymbol{a} \cdot \boldsymbol{b} + \boldsymbol{a} \cdot \boldsymbol{c} $、$(\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c} $ が成り立つことに注意)。
ここで\begin{align*}&a = |\boldsymbol{\mathsf{v}}|^2 \\\\&b = R_0\cdot\boldsymbol{\mathsf{v}} \\\\&c = |R_0|^2 - r^2\end{align*}と置けば、\[ at^2 + 2bt + c = 0 \]であるから、
判別式 $D = b^2 - ac \geq 0$ であれば、\[ t = \frac{-b \pm \sqrt{b^2 - ac}}{a} \]である。
そして今回は $\boldsymbol{\mathsf{v}}$ の大きさを $1$ としているので $|\boldsymbol{\mathsf{v}}| = 1$、すなわち $a = |\boldsymbol{\mathsf{v}}|^2 = 1$ である。
結局 $t$ は\[ t = -b \pm \sqrt{b^2 - c} \]となる。
この解は2つあるが値の小さい方を $tmin$、大きい方を $tmax$ とすれば、レイが $R_0$ を出発して速度 $\boldsymbol{\mathsf{v}}$ で進むとき、円盤上の点 $P$ に衝突するまでにかかる時間が $tmin$ であり、点 $Q$ に衝突するまでにかかる時間が $tmax$ である (ここでは速度ベクトル $\boldsymbol{\mathsf{v}}$ は大きさ $1$ なので $tmin$、$tmax$ を $R_0$ から $P$、$Q$ までの距離とみなすこともできる)。
次のメソッド CollisitonTest_Ray_Disk(..) はレイと円盤の衝突点を求めるものであり、上で述べてきたことを実装したものである。
[CollisitonTest_Ray_Disk(..)]
メソッドの引数はレイの始点 R0、レイの方向 v、円盤の中心 C、円盤の半径 r であり、このメソッドではレイの方向 v は単位ベクトルであることが前提である。
上の解説では円盤の中心 $C$ は原点に置かれているものとして進めていたが、このメソッドではもちろん中心 $C$ は任意の位置で構わない。その場合には単に円盤の中心 $C$ を原点に来るように移動させ、円盤と同じだけの移動をレイにも行えばよい。1行目がその処理であり、locR0 は移動後のレイの始点を表している (レイの始点がどこに移動してもレイの進行方向は同じである)。
円盤とレイが同じだけの移動をしていれば相対的な位置関係は変わらないので、2つの衝突点 $P$、$Q$ に衝突するまでにかかる時間 $tmin$、$tmax$ の値も変わらない。
14行目のifブロックはレイと円盤との衝突が始点 $R_0$ の後ろ側($\boldsymbol{\mathsf{v}}$ を基準にして後ろ側)で発生する場合、衝突とはみなさずに衝突しなかったものとして処理を切り上げるためのものである (これは始点 $R_0$ が円盤の中にある場合も衝突しなかったものとして扱われる)。
しかし その前に2次行列($2\times 2$ 行列)の逆行列について簡単に触れておく。1-4節では3次行列($3\times 3$ 行列)の逆行列について解説したが、具体的には正方行列 $A$ に対して\[ AA^{-1} = A^{-1}A = I\]を満たす行列 $A^{-1}$ を $A$ の逆行列というのであった。$A$ が2次行列の場合は $A^{-1}$、$I$ も2次行列であり、その場合 単位行列 $I$ は\[ I = \begin{pmatrix}1 &0 \\0 &1 \\\end{pmatrix} \]である。
ここで 2次行列 $A$ の各成分を\[ A = \begin{pmatrix}a &b \\c &d \\\end{pmatrix} \]とする。
このとき、$A$ の逆行列 $A^{-1}$ は\begin{equation} A^{-1} = \frac{1}{|A|}\begin{pmatrix}d &-b \\-c &a \\\end{pmatrix} \tag{1}\end{equation}として求められる。
式中の $|A|$ を行列 $A$ の行列式 (determinant)といい、$A$ の逆行列 $A^{-1}$ が存在するためには行列式 $|A|$ が $|A| \neq 0$ でなければならない (詳しくは $|A| \neq 0$ であることが必要十分である)。
行列式 $|A|$ は1つの実数値であり、2次行列の場合は次のように算出される。
\begin{equation}|A| = ad - bc \qquad\qquad\qquad\qquad \tag{2}\end{equation}
(逆行列や行列式については上記の'公式'だけに留め、その導出や具体的な意味などについては省略する)
例えばXY平面上の点 $(p, q)$ を変換行列 $A$ によって適当な位置に移動させたとする。点 $(p, q)$ の移動後の位置を $(p', q')$ とすれば\[ A \begin{pmatrix}p \\q\end{pmatrix} =\begin{pmatrix}p' \\q'\end{pmatrix} \]であるが、この両辺に左から逆行列 $A^{-1}$ を掛けると\[ \begin{pmatrix}p \\q\end{pmatrix} =A^{-1}\begin{pmatrix}p' \\q'\end{pmatrix} \]である。
すなわち 変換行列 $A$ とそれによる移動後の位置 $(p', q')$ のみがわかっている場合でも、$A$ の逆行列 $A^{-1}$ を使えば移動前の位置 $(p, q)$ が求められるということである。
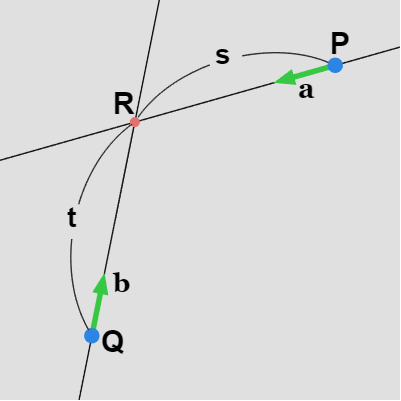
図31 点Pを通る直線と点Qを通る直線、及び交点R では以上をふまえて2直線の交点を求めることについて見ていこう。
XY平面上において2つの直線があり1つは点 $P$ を通る直線で、もう1つは点 $Q$ を通る直線である。この2つの直線の交点を $R$ とし、$P$ から $R$ への方向を表す単位ベクトルを $\overrightarrow{\boldsymbol{a}}$、$Q$ から $R$ への方向を表す単位ベクトルを $\overrightarrow{\boldsymbol{b}}$ とする (図31 ; つまり $\overrightarrow{PR}$、$\overrightarrow{QR}$ を正規化したものが $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ である)。
$P$ から $R$ への距離を $s$、$Q$ から $R$ への距離を $t$ とすれば、\begin{align*}P + s\overrightarrow{\boldsymbol{a}} = R \\\\Q + t\overrightarrow{\boldsymbol{b}} = R\end{align*}であるから、\[ P + s\overrightarrow{\boldsymbol{a}} = Q + t\overrightarrow{\boldsymbol{b}} \]である。
したがって $W = Q - P$ とおけば、\[ s\overrightarrow{\boldsymbol{a}} - t\overrightarrow{\boldsymbol{b}} = Q - P = W \] であるが、$\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$、$W$ の各成分を $(a_x, a_y)$、$(b_x, b_y)$、$(w_x, w_y)$ とすれば上式は\[ s\begin{pmatrix}a_x \\a_y\end{pmatrix} - t\begin{pmatrix}b_x \\b_y\end{pmatrix} = \begin{pmatrix}w_x \\w_y\end{pmatrix} \] と書き換えられる。
さらにこの式は行列によって\[ \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} \begin{pmatrix}s \\t\end{pmatrix} =\begin{pmatrix}w_x \\w_y\end{pmatrix} \]と書き直すことができる。
つまり $A = \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} $とすれば、\[ A\begin{pmatrix}s \\t\end{pmatrix} =\begin{pmatrix}w_x \\w_y\end{pmatrix} \]であるから、$A$ の逆行列 $A^{-1}$ によって $s$、$t$ は次のように求めることができる。
\begin{equation}\begin{pmatrix}s \\t\end{pmatrix} =A^{-1}\begin{pmatrix}w_x \\w_y\end{pmatrix} \tag{3}\end{equation}ここで先程の逆行列 及び行列式の公式 $(1)$、$(2)$ を用いれば $A^{-1}$ は\begin{equation}A^{-1} =\frac{1}{|A|}\begin{pmatrix}-b_y &b_x \\-a_y &a_x \\\end{pmatrix} \tag{4}\end{equation}として求めることができる ($|A| = -a_x b_y + b_x a_y$)。
したがって $(3)$、$(4)$ より $s$、$t$ は次のように算出される。
\begin{equation}\frac{1}{|A|}\begin{pmatrix}-b_y &b_x \\-a_y &a_x \\\end{pmatrix} \begin{pmatrix}w_x \\w_y\end{pmatrix} =\begin{pmatrix}s \\t\end{pmatrix} \tag{5}\end{equation}
以下のメソッド CalcIntersectionOf2Lines(..) はXY平面上の2直線の交点を計算するものである。
[CalcIntersectionOf2Lines(Vector2 P, Vector2 a, Vector2 Q, Vector2 b)]
引数の P、a、Q、b は上記の解説における $P$、$\overrightarrow{\boldsymbol{a}}$、$Q$、$\overrightarrow{\boldsymbol{b}}$ と同じであり、このメソッドは点 P を通る直線と点 $Q$ を通る直線の交点 $R$ を求めるものである (a、b はそれぞれの直線の方向を表す単位ベクトル)。
6~14行目の計算は上で解説したものである。ここでは 7行目の detA (上の解説における行列式 $|A|$)が $0$ でない場合に $P$ から交点 $R$ までの距離 $s$ を求め(10行目)、11行目で交点 $R$ を計算している。
このメソッドは交点 $R$ の座標を返すものであるが戻り値は Vector3 型である。戻り値の x成分、y成分に $R$ の座標がセットされ、z成分には $P$ から $R$ までの距離 $s$ がセットされる ($P$ から $R$ までの距離は返されるが、$Q$ から $R$ までの距離は返されない)。
16行目以降は detA が $0$ の場合である。detA、すなわち $|A|$ が $0$ であるとは2つの単位ベクトル $\overrightarrow{\boldsymbol{a}} (a_x, a_y)$、$\overrightarrow{\boldsymbol{b}} (b_x, b_y)$ が平行であることを意味する。実際、ここで使われている行列 $A$ は具体的には $A = \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} $ であるが、上記の公式 $(2)$ より $|A| = -a_x b_y + b_x a_y$ となる。
したがって、$|A|=0$ ならば $b_x a_y = a_x b_y$、すなわち
\[\frac{a_y}{a_x} = \frac{b_y}{b_x} \]である。
これは 2つの直線の傾きが同じ、つまり 2つの直線が平行であることを意味している。
本来 平面上における2直線が平行である場合には下図32に示されるように、この2直線は交点を持たない。このような場合、このメソッドは Vector3.positiveInfinity を返す (25行目)。
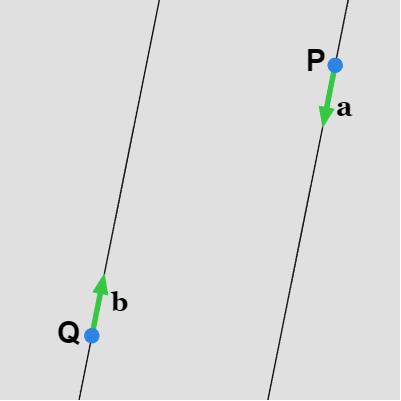
図32 2直線が平行である場合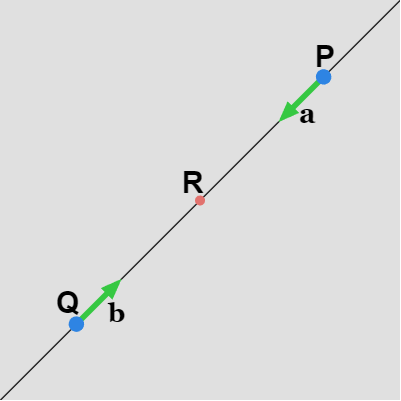 
図33 2直線が重なる場合はP、Qの中間点を交点Rとする
しかし、2つの直線が平行であっても交点が存在する場合がある。それは図33に示されるように2つの直線が完全に重なってしまう場合である。図33のケースでは2直線の方向 $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ だけでなく $P$ と $Q$ を結ぶベクトル $\overrightarrow{W}$ も $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ に対して平行となる。このようなケースは特別な場合として $P$ と $Q$ の中間点を交点 $R$ とし、この中間点を返すようにしている。18行目のifブロックはこの処理のためのものである (IsParallel_BOOL(..) は引数にセットされた2つのベクトルが平行であればtrueを返す)。
では上で述べてきたことを実際のプログラムで実装する。
プログラム実行中にレイ及び長方形を動かすために、以下のキー操作を使用する。
H, J, K, L : 長方形を上下左右に動かす。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムを以下に示す (プログラム中では長方形は Rect という名前で使われている)。
[Code1] (実行結果 図34)
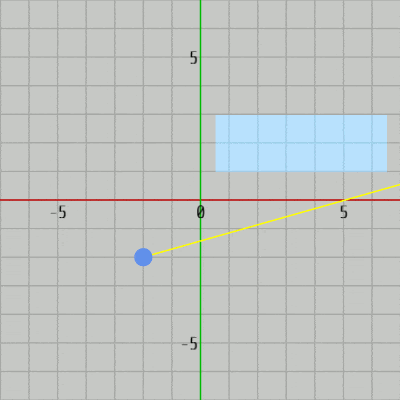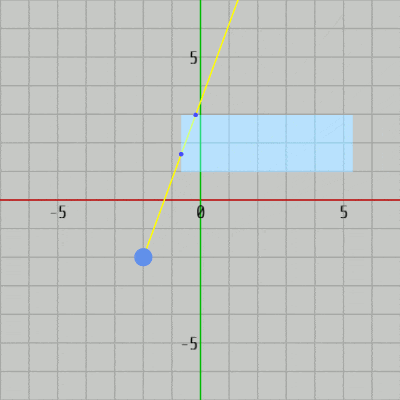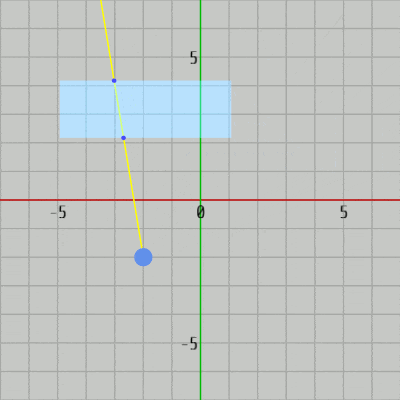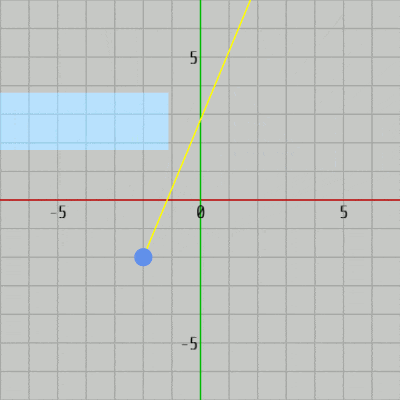
図34 Code1 実行結果 MoveRect() (4行目)は長方形を動かすための補助メソッドであり、ChangeRayDirection() (9行目)はレイの向きを変えるための補助メソッドである。その時点におけるレイの向きは GetRayDirection() (12行目)によって取得できる。
14~16行目はその時点における長方形の左下隅、右上隅の頂点の計算であり、c_initMinMax は初期状態における長方形の左下隅、右上隅の頂点がセットされた配列である (初期状態では長方形は上図1のように中心が原点に置かれた軸平行な長方形であるので左下隅、右上隅の頂点は $(-w/2,-h/2)$、$(w/2,\ h/2)$ である)。
このプログラムでは長方形は軸平行な長方形であるので使われている衝突判定メソッドは CollisionTest_Ray_AABB(..) である (18行目)。レイと長方形が衝突している場合には、その衝突点が表示されるように衝突点がセットされた配列を補助メソッド Hit(..) にセットしている。
H, J, K, L : 長方形を上下左右に動かす。
R : 長方形を反時計周りに回転させる (Shiftと同時押しで時計周りに回転)。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムを以下に示す。
[Code2] (実行結果 図35)
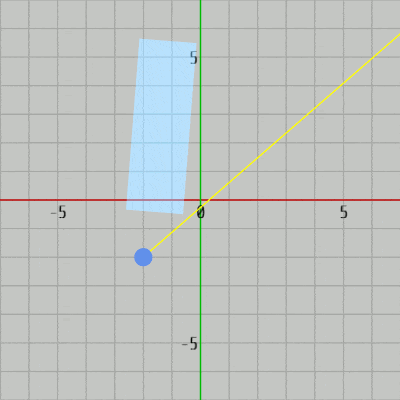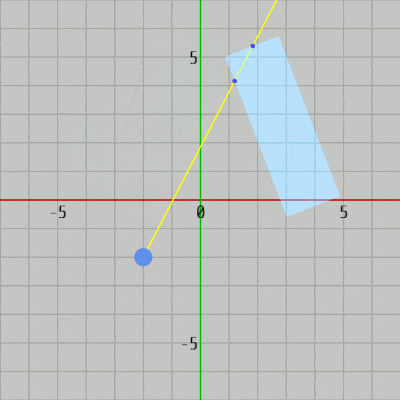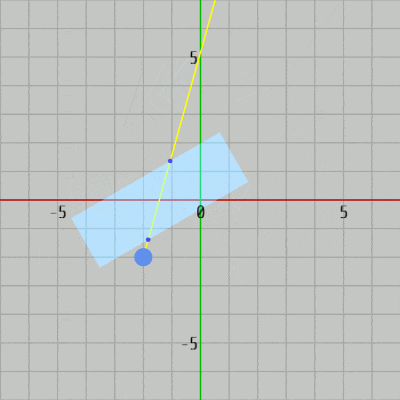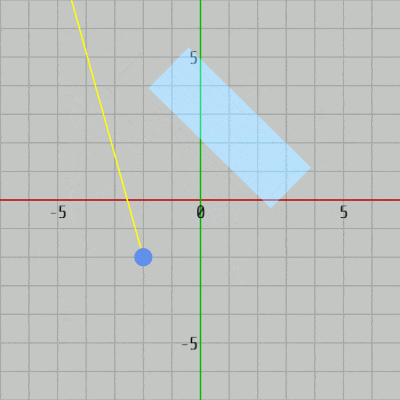
図35 Code2 実行結果 プログラムはCode1とほとんど同じであり、衝突判定のメソッドが軸平行な長方形用のものから一般の長方形用のものに変わっているに過ぎない。16、17行目の ui、uj はその時点における長方形の横の辺、縦の辺の方向を表す単位ベクトルである (ui、uj を求めるにあたって長方形に実行されている変換行列を使用することについては 2-20節参照)。
T (18行目)はその時点での長方形の中心位置である。
このプログラムもCode1と同じくレイと長方形の間に衝突があれば、その衝突点を表示するだけである。今回は長方形が回転している場合も対象とするので衝突判定メソッドは CollisitonTest_Ray_Rect(..) が使われている (20行目 ; 引数に使われている c_RectW、c_RectH は長方形の横の辺、縦の辺の長さを表す定数)。
図36 Disk 初期状態 (半径 1)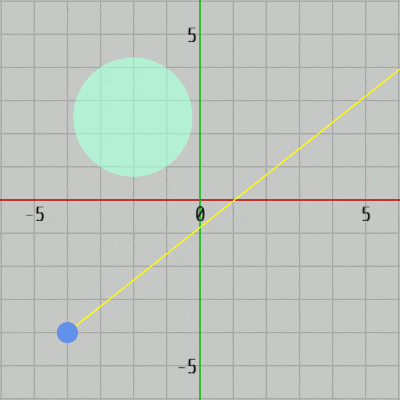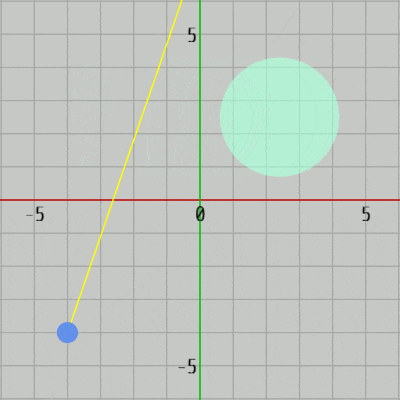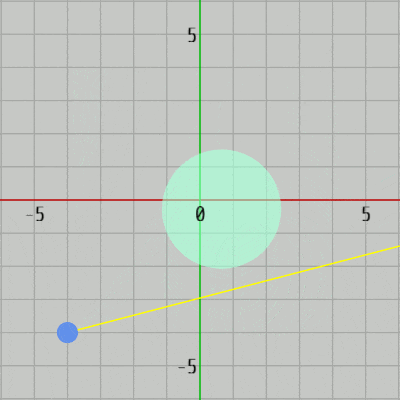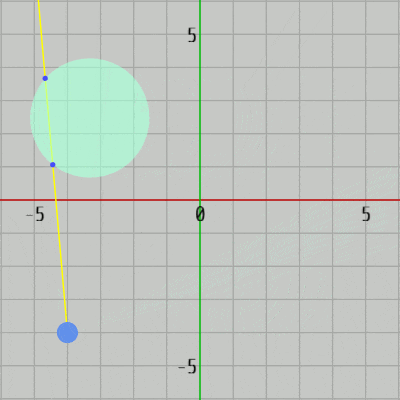 
図37 Code3 実行結果
実行中にDisk及びレイを動かすには以下のキー操作を使用する。
H, J, K, L : Diskを上下左右に動かす。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムは次のとおり。
[Code3] (実行結果 図37)
14行目の GetPosition() によって現時点でのDiskの中心が返される。15行目の transform.localScale.x はDiskに実行されている(x軸方向の)スケール倍率を表すが、初期状態でのDiskの半径は $1$ なのでこの値は現時点でのDiskの半径に相当する。
レイとDiskとの衝突点を求めるには、レイの始点 R0、方向 v、Diskの中心 C、半径 r を上で解説した CollisitonTest_Ray_Disk(..) にセットすればよい。
H, J : 左側の直線を回転させる。
K, L : 右側の直線を回転させる。
プログラムは次のとおり。
[Code3] (実行結果 図38)
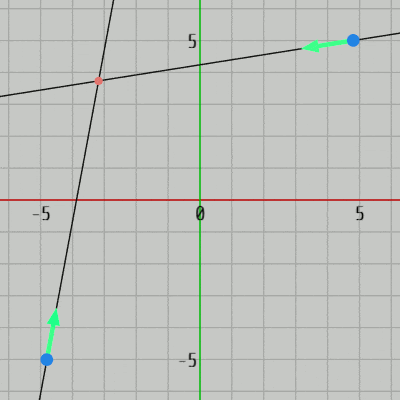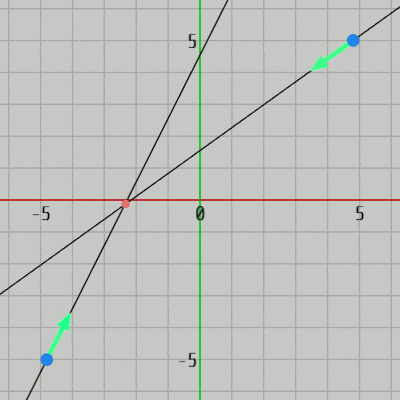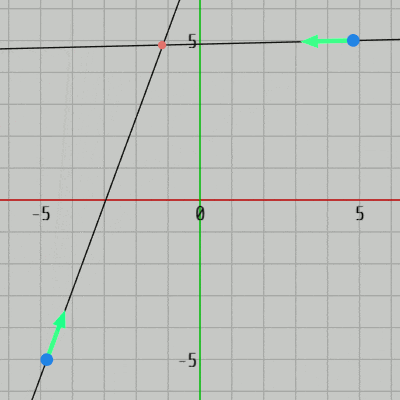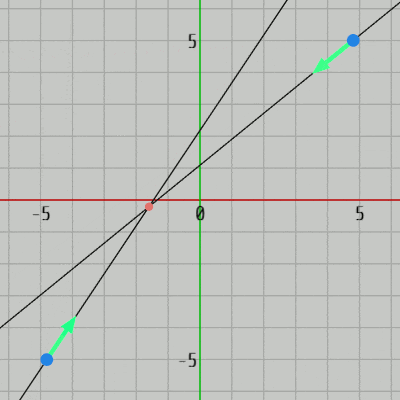
図38 Code4 実行結果 右図は実行結果であるが、図中の青い点は直線上の点であり、緑の矢印は直線の方向を表している (直線上の青い点はプログラム中ではインスタンス変数 P1、P2 として用意されている)。
4行目の RotateLine() は2つの直線を回転させるメソッドであるが、具体的には H、J を押すと左側の直線が反時計周り、時計周りに回転し、K、L を押すと右側の直線が反時計周り、時計周りに回転する。
7、8行目の GetDirection_v#() は各直線の方向を取得するためのメソッドであり、現時点での緑の矢印の方向が返される (返される値は単位ベクトル)。
10行目の CalcIntersectionOf2Lines(..) は上で解説した2直線の交点を求めるメソッドであり、このメソッドに2直線の直線上の点 及び方向をセットすれば2直線の交点が返される (14行目の Dot は交点を表すオブジェクトで、図38における小さな赤い点)。
(参考資料)
https://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-box-intersection.html
https://education.siggraph.org/static/HyperGraph/raytrace/rtinter3.htm
A) 直線 vs 長方形 (Slab Method)
直線と長方形の衝突判定では「Slab Method」というアルゴリズムを用いるが、まずはその解説から始める。図1は横の長さ $w$、縦の長さ $h$ の長方形であり、各辺は x軸、y軸に平行、その中心は原点に置かれている。
この長方形を縦方向に無限に伸ばした領域を「X領域」、横方向に無限に伸ばした領域を「Y領域」と呼ぶことにする。X領域はその横の長さが $w$ でその領域を x軸が貫いており、Y領域はその縦の長さが $h$ でその領域を y軸が貫いている。図から明らかなように長方形はこの2つの領域、X領域、Y領域の交差部分に等しい。
-
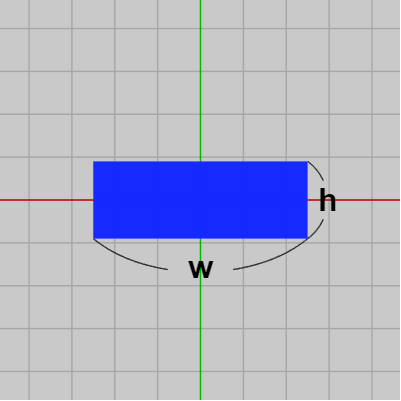図1 -
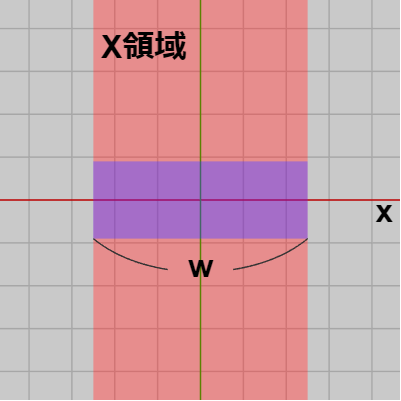図2 X領域 -
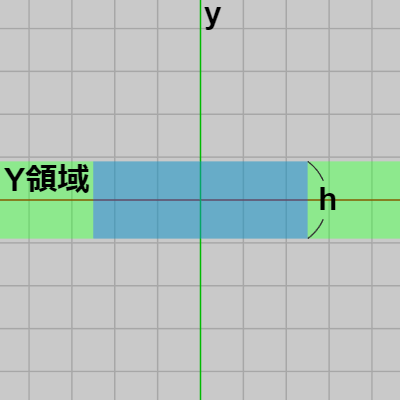図3 Y領域
また XY平面上の点 $R_0$ から半直線を引き、その方向を $\boldsymbol{\mathsf{v}}$ とする (図5)。ここではこの半直線のことをレイ(Ray)と呼ぶことにする。
$\boldsymbol{\mathsf{v}}$ は方向を表すベクトルであるが、以下の解説においては $\boldsymbol{\mathsf{v}}$ を大きさ(速さ) $1$ の速度ベクトルとして扱う。すなわち 図5のレイ(半直線)は矢印の方向に速さ $1$ で進んでいくものとして考える。
今 この半直線と長方形が衝突したとしよう (図6)。
下図7に示されるようにこのときレイは長方形のX領域、Y領域の交差部分を通過する。
レイが始点 $R_0$ を出発してからX領域に入るまでにかかる時間(X領域と最初に衝突するまでにかかる時間)を $inX$ とし、$R_0$ を出発してからX領域を出るまでにかかる時間(X領域と2回目に衝突するまでにかかる時間)を $outX$ とする (図8)。
同様に レイが $R_0$ を出発してからY領域に入るまでにかかる時間を $inY$、$R_0$ を出発してからY領域を出るまでにかかる時間にかかる時間を $outY$ とする。
($inX$、$outX$、$inY$、$outY$ は経過時間である。距離や位置ではないことに注意)
上図の場合、レイは始点 $R_0$ を出発してからまず X領域に入り、次にY領域に入る。その後 Y領域を出てから最後にX領域を出る。上で述べたように長方形はX領域、Y領域の交差部分であるから、レイが長方形の中を進んでいる間はX領域、Y領域の両方にいることになる。
レイがX領域にいるのは $inX$~$outX$ の間であり、レイがY領域にいるのは $inY$~$outY$ の間である。したがって、レイが長方形の中を進む場合(それはレイが長方形と衝突することを意味する)はこの2つの区間 $inX$~$outX$、$inY$~$outY$ に重なりがあるということである。
2-19節で見たように2つの区間 $inX$~$outX$、$inY$~$outY$ の間に重なりがあるかどうかは以下の条件式を調べればよい。
\[ inX < outY\ \ \&\&\ \ inY < outX \]今回の例でいえばこの条件式が成り立つならばレイと長方形は衝突するということである (2つの区間の重なりの部分は、レイが長方形の中を進んでいる時間に相当する。図9の場合は2つの区間の重なりは $inY$~$outY$ であるが、この区間においてレイは長方形の中を進んでいる)。
下図はレイと長方形が衝突する別のケースである。経過時間の大小関係は $inY < inX < outY < outX$ であり、2つの区間 $inX$~$outX$、$inY$~$outY$ は $inX$~$outY$ において重なっているが、図に示されるようにこの区間においてレイは長方形の中を進んでいる。
以下の2つの図はレイと長方形が衝突していないケースであるが、いずれの場合にも上記の重なり判定の条件式が成立していないことがわかるであろう (左図の場合は $inX > outY$ であり、右図の場合は $inY > outX$ になっている)。
レイと長方形との衝突判定ではレイがある領域に入る前に、別の領域から出てしまうようなことがあれば両者が衝突することはない。上図11の場合はレイがX領域に入る前にY領域を出てしまっており、図12の場合はレイがY領域に入る前にX領域を出てしまっている。
レイと長方形が衝突する場合とは、レイがX領域を進んでいる間にY領域に入る、あるいはレイがY領域を進んでいる間にX領域に入る場合のいずれかである。そしてその場合にはレイが(最初の領域ではなく)第2の領域に入る時点で長方形との衝突が発生する。
例えば レイがY領域を進んでいる間にX領域に入る場合には、レイが出発してから $inX$ 経過した時点でレイと長方形が衝突することになる (上図10の衝突はこのケースである)。
(使われる変数が増えてきたが、$inX$、$outX$、$inY$、$outY$ は経過時間であり、$(xmin,\ ymin)$、$(xmax,\ ymax)$ は長方形の頂点座標である)
$inX$ や $outX$ を求めるには次のように考えればよい。
上で定めたことに従えばレイが始点 $R_0$ を速度 $\boldsymbol{\mathsf{v}}$ で出発してからX領域に(最初に)衝突するまでにかかる時間が $inX$ であるが、このときのレイとX領域との衝突点を $P$ とする (図14)。また、速度ベクトル $\boldsymbol{\mathsf{v}}$ の x成分を $\boldsymbol{\mathsf{v}}.x$、y成分を $\boldsymbol{\mathsf{v}}.y$ とする。
速度ベクトル $\boldsymbol{\mathsf{v}}$ は単位ベクトルであるからその大きさ(速さ)は $1$ である。したがって、レイが $R_0$ を出発して、$\boldsymbol{\mathsf{v}}$ の方向に速さ $1$ で進むとき、時間 $inX$ 後に点 $P$ に衝突するわけであるが、この同じ時間の間に $\boldsymbol{\mathsf{v}}$ の x成分 $\boldsymbol{\mathsf{v}}.x$ は $R_0$ から図14の $P'$ まで進むことになる。
$R_0$ から $P'$ に進む際には y軸方向の移動がないので、その距離は $P'\!.x - R_0.x$ であり、$P'\!.x = xmin$ であるため、結局\[ (xmin - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = inX \]となり、$outX$ は\[ (xmax - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = outX \]として求められる。
$inY$、$outY$ の求め方も同様である。ここではレイとY領域の最初の衝突点を $Q$ とする (図15)。この場合 レイが $R_0$ を出発して、$\boldsymbol{\mathsf{v}}$ の方向に速さ $1$ で進むとき、時間 $inY$ 後に点 $Q$ に衝突するわけであるが、この同じ時間の間に $\boldsymbol{\mathsf{v}}$ の y成分 $\boldsymbol{\mathsf{v}}.y$ は $R_0$ から図15の $Q'$ まで進むことになる。
$R_0$ から $Q'$ に進む際には x軸方向の移動がないので、その距離は $Q'\!.y - R_0.y$ であり、$Q'\!.y = ymin$ であるため、結局\begin{align*}(ymin - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = inY \\\\(ymax - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = outY \end{align*}となる。
上の例では長方形の左下隅の座標を $(xmin,\ ymin)$、右上隅の座標を $(xmax,\ ymax)$ としたとき、$inX$ や $inY$ を求める際には $xmin$ や $ymin$ が使われ、$outX$ や $outY$ を求める際には $xmax$ や $ymax$ が使われた。しかし、一般には必ずしもこれは当てはまらない。
例えば、レイの始点 $R_0$ 及びその方向 $\boldsymbol{\mathsf{v}}$ が上左図の場合には $inX$、$outX$ は\begin{align*}(xmax - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = inX \\\\(xmin - R_0.\!x)\ /\ \boldsymbol{\mathsf{v}}.x = outX \end{align*}となるし、$R_0$、$\boldsymbol{\mathsf{v}}$ が上右図の場合には $inY$、$outY$ は\begin{align*}(ymax - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = inY \\\\(ymin - R_0.\!y)\ /\ \boldsymbol{\mathsf{v}}.y = outY \end{align*}となる。つまり レイと長方形の相対的な位置関係によって $inX$、$inY$、$outX$、$outY$ の求め方は変わってくるのである。
しかし、それらの値を求める際には場合分けをすることなく簡単に求めることができる。例えば $inX$、$outX$ の場合であれば、上図14の場合のように $inX$ は $xmin$ を使って計算し、$outX$ は $xmax$ を使って計算する。そして、$inX$ が $outX$ よりも大きい場合には両者を入れ替えればよい。それだけである。
上の例における長方形はその各辺が x軸、y軸に平行、すなわち 軸平行な長方形であった。以下では長方形が軸平行でない場合、すなわち 長方形が回転している場合について考える (以下の内容は 2-20節と実質的には同じである)。
各辺の長さが $w$、$h$ の長方形とレイが下図18に示される状態で置かれている。図中の $T$ は長方形の中心である。
$T$ を通り長方形の長い辺に平行な直線を i 軸、同じく $T$ を通り長方形の短い辺に平行な直線を j 軸とする。また i 軸、j 軸の方向を表す単位ベクトルを $\boldsymbol{u_i}$、$\boldsymbol{u_j}$ とする (図19 ; 以下ではこの $T$ を原点とする座標系を簡単に ij 座標系と呼ぶことにする)。
この ij 座標系におけるレイの始点 $R_0$、及びその方向 $\boldsymbol{\mathsf{v}}$ を求めよう。
上記では $R_0$ の x座標、y座標を $R_0.\!x$、$R_0.\!y$ として用いたが、この $R_0.\!x$、$R_0.\!y$ は詳しくは始点 $R_0$ が xy座標系の原点から x軸方向に $R_0.\!x$、y軸方向に $R_0.\!y$ だけ離れていることを意味する (図20)。
したがって $R_0$ の ij 座標系での値を求めるには、$R_0$ が ij 座標系の原点 $T$ から i 軸方向、j 軸方向にどれだけ離れているかを調べる必要がある。ここではそれらの距離を $s$、$t$ とする (図21)。
$T$ と $R_0$ を結ぶベクトルを $\boldsymbol{m}\ (= R_0 - T)$ とすれば、i 軸方向の距離 $s$、j 軸方向の距離 $t$ は次のように求められる。
\begin{align*} \boldsymbol{m} \cdot \boldsymbol{u_i} = s \\\\ \boldsymbol{m} \cdot \boldsymbol{u_j} = t\end{align*}つまり $R_0$ の ij 座標系における座標は $(\boldsymbol{m} \cdot \boldsymbol{u_i},\ \boldsymbol{m} \cdot \boldsymbol{u_j})$ である。
レイの方向 $\boldsymbol{\mathsf{v}}$ の ij 座標系での値を求める場合も同様の手順で進めればよい。上記と同じく $\boldsymbol{\mathsf{v}}$ の x座標、y座標を $\boldsymbol{\mathsf{v}}.x$、$\boldsymbol{\mathsf{v}}.y$ とすれば、これらの値が意味することは xy座標系において $\boldsymbol{\mathsf{v}}$ の始点から終点までの距離は、x軸方向に $\boldsymbol{\mathsf{v}}.x$、y軸方向に $\boldsymbol{\mathsf{v}}.y$ だけ離れているということである。(図22はわかりやすくするために $\boldsymbol{\mathsf{v}}$ の始点を xy座標系の原点に置いたときのものである。この図における $\boldsymbol{\mathsf{v}}.x$、$\boldsymbol{\mathsf{v}}.y$ の値はいずれもマイナスである)。
$\boldsymbol{\mathsf{v}}$ の ij 座標系での値を求めるには、$\boldsymbol{\mathsf{v}}$ の始点を ij 座標系の原点 $T$ に置いたときに、$\boldsymbol{\mathsf{v}}$ の終点が $T$ から i 軸方向、j 軸方向にどれだけ離れているかを計算すればよい。
それらの距離をここでも $s$、$t$ とすれば (図23)、\begin{align*} \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i} = s \\\\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j} = t\end{align*}となる。つまり $\boldsymbol{\mathsf{v}}$ の ij 座標系における値は $(\boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_i},\ \boldsymbol{\mathsf{v}} \cdot \boldsymbol{u_j})$ である (これはすなわち $\boldsymbol{\mathsf{v}}$ の ij 座標系における方向である)。
$R_0$、$\boldsymbol{\mathsf{v}}$ の ij 座標系での値がわかれば、あとは i 軸、j 軸に平行な長方形とレイとの衝突を考えることと同じである (図24)。そしてこの場合には長方形の中心 $T$ は ij 座標系の原点でもあるので、各辺の長さを $w$、$h$ とすれば長方形の左下隅の頂点 $(xmin,\ ymin)$ の値は $(-w/2, -h/2)$ であり、右上隅の頂点 $(xmax,\ ymax)$ の値は $(w/2,\ h/2)$ である (図25)。
ij 座標系においてレイと長方形の衝突点を求めた後はその衝突点の座標を xy座標系での値に変換しなければならない。始点 $R_0$ から出発したレイが長方形と衝突するまでにかかる時間は ij 座標系において測っても、xy座標系において測っても同じである (ここでは $|\boldsymbol{\mathsf{v}|=1}$ なので時間ではなく距離と考えてもよい。すなわち衝突点までの距離は ij 座標系で測っても xy座標系で測っても同じである)。
したがって ij 座標系においては実際には衝突点を計算する必要はなく、衝突までにかかる時間がわかればよい。ここでは長方形に最初に衝突するまでにかかる時間を $k_0$、長方形に2回目に衝突する(長方形から出ていくとき)までにかかる時間を $k_1$ とする。そのとき衝突点は簡単に\[ R_0 + k_0 \boldsymbol{\mathsf{v}} = P_0 \qquad\qquad R_0 + k_1 \boldsymbol{\mathsf{v}} = P_1\]として求められる ($P_0$ が最初の衝突点)。
次のメソッド CollisionTest_Ray_AABB(..) はレイと軸平行な長方形との衝突判定メソッドであり、上で述べてきたことを実装したものである。
[CollisionTest_Ray_AABB(..)]
Vector2[] CollisionTest_Ray_AABB(Vector2 R0, Vector2 v, Vector2[] min_max)
{
const float eps = 0.000001f;
float xmin = min_max[0].x;
float ymin = min_max[0].y;
float xmax = min_max[1].x;
float ymax = min_max[1].y;
float inX, outX;
if (THUtil.IsZero(v.x))
{
if (R0.x < xmin || xmax < R0.x) { return null; }
inX = float.NegativeInfinity;
outX = float.PositiveInfinity;
}
else
{
inX = (xmin - R0.x) / v.x;
outX = (xmax - R0.x) / v.x;
if (v.x < -eps) { THUtil.Swap(ref inX, ref outX); }
}
float inY, outY;
if (THUtil.IsZero(v.y))
{
if (R0.y < ymin || ymax < R0.y) { return null; }
inY = float.NegativeInfinity;
outY = float.PositiveInfinity;
}
else
{
inY = (ymin - R0.y) / v.y;
outY = (ymax - R0.y) / v.y;
if (v.y < -eps) { THUtil.Swap(ref inY, ref outY); }
}
if (!(inX < outY && inY < outX)) { return null; }
if (inX < 0.0f && inY < 0.0f) { return null; }
float tmin = Mathf.Max(inX, inY);
float tmax = Mathf.Min(outX, outY);
return new Vector2[] { R0 + tmin * v, R0 + tmax * v };
}
第1引数 R0 はレイの始点、第2引数 v はレイの方向を表す単位ベクトル、第3引数 min_max は長方形の左下隅、右上隅の頂点(上図13)がセットされた配列である (Vector2[]型)。
プログラム中で使われている各変数 xmin、ymin、inX、outX などは上の解説のものと意味は同じである。
11~23行目はレイの始点 R0 からX領域に衝突するまでの経過時間 inX、X領域から出るまでの経過時間 outX の計算であり、26~38行目は R0 からY領域に衝突するまでの経過時間 inY、Y領域から出るまでの経過時間 outY の計算である。
どちらも if/else ブロックで記述されているが、if ブロックはレイの方向 v が x軸あるいは y軸に平行な場合、else ブロックの方は v が x軸にも y軸にも平行でない場合であり、else ブロック内の計算は上の解説で述べた通りである。THUtil.Swap(ref a, ref b) はカスタムライブラリーのメソッドで、第1引数の値と第2引数の値を入れ替えるためのものであり、inX が outX よりも小さい値になるように、inY が outY よりも小さい値になるようにするために使用している。
v が x軸あるいは y軸に平行な場合については後に回すとして、先に40行目以降を見ていく。
41行目の判定はレイと長方形が衝突しているかを調べるものであり、\[ inX < outY\ \ \&\&\ \ inY < outX \]が成り立つ場合には両者が衝突している。
ただしレイと長方形が衝突していても衝突点がレイの始点 R0 から後ろの方向(v を基準にして後ろ)にある場合には、衝突とはみなさずに衝突していないものとして null を返す (43行目 ; この場合には inX、inY ともにマイナスになる)。
衝突している場合にはレイと長方形の衝突点は2つある (1つの場合も重複しているものとして考える)。1つはレイの始点から近い方の衝突点であり、もう1つは遠い方の衝突点である。このメソッドではその2つの衝突点を配列として返すが最初の要素に近い方の衝突点、2番目の要素に遠い方の衝突点をセットする (48行目)。
最後にレイの方向 v が x軸あるいは y軸に平行である場合について見ていこう。上の解説ではレイの方向 v は x軸にも y軸にも平行でないことを前提としていたが、もし v が x軸あるいは y軸に平行である場合は特別な処理が必要になる (11、26行目の if ブロック)。
例えば v が y軸に平行( v.x==0 )であるとしよう。この場合には図27に示されるようにレイの始点 R0 がX領域に含まれていなければ衝突することはないので、この時点で衝突していないことを示す null を返す (13行目)。X領域に含まれている場合でもレイと長方形は衝突するが、レイとX領域は衝突することはない。そのため inX、outX には特別に NegativeInfinity、PositiveInfinity をセットしている (15、16行目)。
v が x軸に平行( v.y==0 )も同様である (図28)。この場合には R0 がY領域に含まれていなければ衝突することはないので null を返し(28行目)、Y領域に含まれている場合は inY、outY には NegativeInfinity、PositiveInfinity をセットする (30、31行目)。
次のメソッド CollisitonTest_Ray_Rect(..) はレイと長方形との衝突判定メソッドであり、このメソッドでは傾きのある長方形も対象とする。
[CollisitonTest_Ray_Rect(..)]
Vector2[] CollisionTest_Ray_Rect(Vector2 R0, Vector2 v,
Vector2 T, Vector2 ui, Vector2 uj, float w, float h)
{
Vector2 m = R0 - T;
float s = Vector2.Dot(m, ui);
float t = Vector2.Dot(m, uj);
Vector2 locR0 = new Vector2(s, t);
s = Vector2.Dot(v, ui);
t = Vector2.Dot(v, uj);
Vector2 locV = new Vector2(s, t).normalized;
Vector2 max = new Vector2(w / 2, h / 2);
Vector2 min = -max;
float[] ti = ComputeT_Ray_AABB(locR0, locV, new Vector2[] { min, max });
if (ti == null) { return null; }
return new Vector2[] { R0 + ti[0] * v, R0 + ti[1] * v };
}
4~7行目までが ij 座標系での R0 の値の計算、9~11行目までが ij 座標系での v の値の計算であり、それぞれ locR0、locV というローカル変数にセットされる。
そして先程述べたように ij 座標系で衝突判定を行う場合は長方形の中心 T は原点に位置し、長方形の各辺は i 軸、j 軸に平行であるので衝突判定は、ij 座標系においてレイと軸平行な長方形の衝突判定を行うことと同じである。その際に使用する長方形の左下隅、右上隅の頂点は長方形の各辺の長さが w、h であるとき、(-w/2, -h/2)、(w/2, h/2) となる (13~15行目)。
15行目の ComputeT_Ray_AABB(..) はレイと長方形が衝突するまでにかかる時間を計算するメソッドであり、これは ij 座標系における計算である。衝突した場合には ti に2つのfloat値がセットされるが、これは上で述べた最初の衝突までにかかる時間、2回目の衝突までにかかる時間である。すなわち ti[0]、ti[1] は先ほどの $k_0$、$k_1$ のことであり、18行目の計算は以下の計算に相当する。
\[ R_0 + k_0 \boldsymbol{\mathsf{v}} = P_0 \qquad\qquad R_0 + k_1 \boldsymbol{\mathsf{v}} = P_1\]
上記の CollisionTest_Ray_AABB(..) と内容自体は同じである。
[ComputeT_Ray_AABB(..)]
float[] ComputeT_Ray_AABB(Vector2 R0, Vector2 v, Vector2[] min_max)
{
const float eps = 0.000001f;
float xmin = min_max[0].x;
float ymin = min_max[0].y;
float xmax = min_max[1].x;
float ymax = min_max[1].y;
float inX, outX;
if (THUtil.IsZero(v.x))
{
if (R0.x < xmin || xmax < R0.x) { return null; }
inX = float.NegativeInfinity;
outX = float.PositiveInfinity;
}
else
{
inX = (xmin - R0.x) / v.x;
outX = (xmax - R0.x) / v.x;
if (v.x < -eps) { THUtil.Swap(ref inX, ref outX); }
}
float inY, outY;
if (THUtil.IsZero(v.y))
{
if (R0.y < ymin || ymax < R0.y) { return null; }
inY = float.NegativeInfinity;
outY = float.PositiveInfinity;
}
else
{
inY = (ymin - R0.y) / v.y;
outY = (ymax - R0.y) / v.y;
if (v.y < -eps) { THUtil.Swap(ref inY, ref outY); }
}
if (!(inX < outY && inY < outX)) { return null; }
if (inX < 0.0f && inY < 0.0f) { return null; }
float tmin = Mathf.Max(inX, inY);
float tmax = Mathf.Min(outX, outY);
return new float[] { tmin, tmax };
}
B) 直線 vs 円盤
続いて直線と円盤の衝突点を求める問題について考える。円盤の中心を $C$、半径を $r$ とし、ここでも直線を表すオブジェクトとして点 $R_0$ を始点とし、$\boldsymbol{\mathsf{v}}$ の方向に進む半直線 レイ を用いる (図29 ; 今までと同様に $\boldsymbol{\mathsf{v}}$ は大きさ(速さ) $1$ の速度ベクトルとする)。 簡単のため円盤の中心 $C$ が原点に置かれている場合で進める。
またここではレイが始点 $R_0$ を出発してから円盤との最初の衝突点を $P$、第2の衝突点を $Q$ とする (図30)。レイが $R_0$ を速度 $\boldsymbol{\mathsf{v}}$ で出発して点 $P$ に衝突するまでにかかる時間を $t$ とすれば\[ R_0 + t\boldsymbol{\mathsf{v}} = P \]である。
$P$ は、中心 $C$、半径 $r$ の円周上の点であり、ここでは $C$ は原点に置かれているから\[|P - C| = |P - O| = |P| = r\]である (式中の $O$ は原点)。
すなわち $|R_0 + t\boldsymbol{\mathsf{v}}| = r\ (= |P|)\ $ であり、この両辺を2乗すると\[|R_0 + t\boldsymbol{\mathsf{v}}|^2 = r^2\]である。
したがって、\begin{align*}&|R_0 + t\boldsymbol{\mathsf{v}}|^2 - r^2 \\\\=\ &(R_0 + t\boldsymbol{\mathsf{v}})\cdot(R_0 + t\boldsymbol{\mathsf{v}}) - r^2 \\\\=\ &|\boldsymbol{\mathsf{v}}|^2t^2 + 2(R_0\cdot \boldsymbol{\mathsf{v}})t + (|R_0|^2 - r^2) \\\\=\ &0\end{align*}と展開される (ベクトルの内積に関しては分配法則、すなわち $\boldsymbol{a} \cdot (\boldsymbol{b} + \boldsymbol{c}) = \boldsymbol{a} \cdot \boldsymbol{b} + \boldsymbol{a} \cdot \boldsymbol{c} $、$(\boldsymbol{a} + \boldsymbol{b}) \cdot \boldsymbol{c} = \boldsymbol{a} \cdot \boldsymbol{c} + \boldsymbol{b} \cdot \boldsymbol{c} $ が成り立つことに注意)。
ここで\begin{align*}&a = |\boldsymbol{\mathsf{v}}|^2 \\\\&b = R_0\cdot\boldsymbol{\mathsf{v}} \\\\&c = |R_0|^2 - r^2\end{align*}と置けば、\[ at^2 + 2bt + c = 0 \]であるから、
判別式 $D = b^2 - ac \geq 0$ であれば、\[ t = \frac{-b \pm \sqrt{b^2 - ac}}{a} \]である。
そして今回は $\boldsymbol{\mathsf{v}}$ の大きさを $1$ としているので $|\boldsymbol{\mathsf{v}}| = 1$、すなわち $a = |\boldsymbol{\mathsf{v}}|^2 = 1$ である。
結局 $t$ は\[ t = -b \pm \sqrt{b^2 - c} \]となる。
この解は2つあるが値の小さい方を $tmin$、大きい方を $tmax$ とすれば、レイが $R_0$ を出発して速度 $\boldsymbol{\mathsf{v}}$ で進むとき、円盤上の点 $P$ に衝突するまでにかかる時間が $tmin$ であり、点 $Q$ に衝突するまでにかかる時間が $tmax$ である (ここでは速度ベクトル $\boldsymbol{\mathsf{v}}$ は大きさ $1$ なので $tmin$、$tmax$ を $R_0$ から $P$、$Q$ までの距離とみなすこともできる)。
次のメソッド CollisitonTest_Ray_Disk(..) はレイと円盤の衝突点を求めるものであり、上で述べてきたことを実装したものである。
[CollisitonTest_Ray_Disk(..)]
public static Vector2[] CollisionTest_Ray_Disk(Vector2 R0, Vector2 v,
Vector2 C, float r)
{
Vector2 locR0 = R0 - C;
float b = Vector2.Dot(locR0, v);
float c = locR0.sqrMagnitude - r * r;
float D = b * b - c;
if(D < 0.0f) { return null; }
float tmin = -b - Mathf.Sqrt(D);
float tmax = -b + Mathf.Sqrt(D);
if (tmin < 0.0f) { return null; }
Vector2 P = R0 + tmin * v;
Vector2 Q = R0 + tmax * v;
return new Vector2[] { P, Q };
}
メソッドの引数はレイの始点 R0、レイの方向 v、円盤の中心 C、円盤の半径 r であり、このメソッドではレイの方向 v は単位ベクトルであることが前提である。
上の解説では円盤の中心 $C$ は原点に置かれているものとして進めていたが、このメソッドではもちろん中心 $C$ は任意の位置で構わない。その場合には単に円盤の中心 $C$ を原点に来るように移動させ、円盤と同じだけの移動をレイにも行えばよい。1行目がその処理であり、locR0 は移動後のレイの始点を表している (レイの始点がどこに移動してもレイの進行方向は同じである)。
円盤とレイが同じだけの移動をしていれば相対的な位置関係は変わらないので、2つの衝突点 $P$、$Q$ に衝突するまでにかかる時間 $tmin$、$tmax$ の値も変わらない。
14行目のifブロックはレイと円盤との衝突が始点 $R_0$ の後ろ側($\boldsymbol{\mathsf{v}}$ を基準にして後ろ側)で発生する場合、衝突とはみなさずに衝突しなかったものとして処理を切り上げるためのものである (これは始点 $R_0$ が円盤の中にある場合も衝突しなかったものとして扱われる)。
C) 直線 vs 直線
最後に直線と直線の衝突点(2直線の交点)の求め方について解説する。しかし その前に2次行列($2\times 2$ 行列)の逆行列について簡単に触れておく。1-4節では3次行列($3\times 3$ 行列)の逆行列について解説したが、具体的には正方行列 $A$ に対して\[ AA^{-1} = A^{-1}A = I\]を満たす行列 $A^{-1}$ を $A$ の逆行列というのであった。$A$ が2次行列の場合は $A^{-1}$、$I$ も2次行列であり、その場合 単位行列 $I$ は\[ I = \begin{pmatrix}1 &0 \\0 &1 \\\end{pmatrix} \]である。
ここで 2次行列 $A$ の各成分を\[ A = \begin{pmatrix}a &b \\c &d \\\end{pmatrix} \]とする。
このとき、$A$ の逆行列 $A^{-1}$ は\begin{equation} A^{-1} = \frac{1}{|A|}\begin{pmatrix}d &-b \\-c &a \\\end{pmatrix} \tag{1}\end{equation}として求められる。
式中の $|A|$ を行列 $A$ の行列式 (determinant)といい、$A$ の逆行列 $A^{-1}$ が存在するためには行列式 $|A|$ が $|A| \neq 0$ でなければならない (詳しくは $|A| \neq 0$ であることが必要十分である)。
行列式 $|A|$ は1つの実数値であり、2次行列の場合は次のように算出される。
\begin{equation}|A| = ad - bc \qquad\qquad\qquad\qquad \tag{2}\end{equation}
(逆行列や行列式については上記の'公式'だけに留め、その導出や具体的な意味などについては省略する)
例えばXY平面上の点 $(p, q)$ を変換行列 $A$ によって適当な位置に移動させたとする。点 $(p, q)$ の移動後の位置を $(p', q')$ とすれば\[ A \begin{pmatrix}p \\q\end{pmatrix} =\begin{pmatrix}p' \\q'\end{pmatrix} \]であるが、この両辺に左から逆行列 $A^{-1}$ を掛けると\[ \begin{pmatrix}p \\q\end{pmatrix} =A^{-1}\begin{pmatrix}p' \\q'\end{pmatrix} \]である。
すなわち 変換行列 $A$ とそれによる移動後の位置 $(p', q')$ のみがわかっている場合でも、$A$ の逆行列 $A^{-1}$ を使えば移動前の位置 $(p, q)$ が求められるということである。
XY平面上において2つの直線があり1つは点 $P$ を通る直線で、もう1つは点 $Q$ を通る直線である。この2つの直線の交点を $R$ とし、$P$ から $R$ への方向を表す単位ベクトルを $\overrightarrow{\boldsymbol{a}}$、$Q$ から $R$ への方向を表す単位ベクトルを $\overrightarrow{\boldsymbol{b}}$ とする (図31 ; つまり $\overrightarrow{PR}$、$\overrightarrow{QR}$ を正規化したものが $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ である)。
$P$ から $R$ への距離を $s$、$Q$ から $R$ への距離を $t$ とすれば、\begin{align*}P + s\overrightarrow{\boldsymbol{a}} = R \\\\Q + t\overrightarrow{\boldsymbol{b}} = R\end{align*}であるから、\[ P + s\overrightarrow{\boldsymbol{a}} = Q + t\overrightarrow{\boldsymbol{b}} \]である。
したがって $W = Q - P$ とおけば、\[ s\overrightarrow{\boldsymbol{a}} - t\overrightarrow{\boldsymbol{b}} = Q - P = W \] であるが、$\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$、$W$ の各成分を $(a_x, a_y)$、$(b_x, b_y)$、$(w_x, w_y)$ とすれば上式は\[ s\begin{pmatrix}a_x \\a_y\end{pmatrix} - t\begin{pmatrix}b_x \\b_y\end{pmatrix} = \begin{pmatrix}w_x \\w_y\end{pmatrix} \] と書き換えられる。
さらにこの式は行列によって\[ \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} \begin{pmatrix}s \\t\end{pmatrix} =\begin{pmatrix}w_x \\w_y\end{pmatrix} \]と書き直すことができる。
つまり $A = \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} $とすれば、\[ A\begin{pmatrix}s \\t\end{pmatrix} =\begin{pmatrix}w_x \\w_y\end{pmatrix} \]であるから、$A$ の逆行列 $A^{-1}$ によって $s$、$t$ は次のように求めることができる。
\begin{equation}\begin{pmatrix}s \\t\end{pmatrix} =A^{-1}\begin{pmatrix}w_x \\w_y\end{pmatrix} \tag{3}\end{equation}ここで先程の逆行列 及び行列式の公式 $(1)$、$(2)$ を用いれば $A^{-1}$ は\begin{equation}A^{-1} =\frac{1}{|A|}\begin{pmatrix}-b_y &b_x \\-a_y &a_x \\\end{pmatrix} \tag{4}\end{equation}として求めることができる ($|A| = -a_x b_y + b_x a_y$)。
したがって $(3)$、$(4)$ より $s$、$t$ は次のように算出される。
\begin{equation}\frac{1}{|A|}\begin{pmatrix}-b_y &b_x \\-a_y &a_x \\\end{pmatrix} \begin{pmatrix}w_x \\w_y\end{pmatrix} =\begin{pmatrix}s \\t\end{pmatrix} \tag{5}\end{equation}
以下のメソッド CalcIntersectionOf2Lines(..) はXY平面上の2直線の交点を計算するものである。
[CalcIntersectionOf2Lines(Vector2 P, Vector2 a, Vector2 Q, Vector2 b)]
public static Vector3 CalcIntersectionOf2Lines(Vector2 P, Vector2 a, Vector2 Q, Vector2 b)
{
a = a.normalized;
b = b.normalized;
Vector2 W = Q - P;
float detA = -a.x * b.y + a.y * b.x;
if (!THUtil.IsZero(detA))
{
float s = (-b.y * W.x + b.x * W.y) / detA;
Vector3 R = P + s * a;
R.z = s;
return R;
}
// 以下は detA == 0 (a と b が平行な場合)
if(IsParallel_BOOL(W, a))
{
Vector3 R = (P + Q) * 0.5f;
R.z = W.magnitude * 0.5f;
return R;
}
return Vector3.positiveInfinity;
}
引数の P、a、Q、b は上記の解説における $P$、$\overrightarrow{\boldsymbol{a}}$、$Q$、$\overrightarrow{\boldsymbol{b}}$ と同じであり、このメソッドは点 P を通る直線と点 $Q$ を通る直線の交点 $R$ を求めるものである (a、b はそれぞれの直線の方向を表す単位ベクトル)。
6~14行目の計算は上で解説したものである。ここでは 7行目の detA (上の解説における行列式 $|A|$)が $0$ でない場合に $P$ から交点 $R$ までの距離 $s$ を求め(10行目)、11行目で交点 $R$ を計算している。
このメソッドは交点 $R$ の座標を返すものであるが戻り値は Vector3 型である。戻り値の x成分、y成分に $R$ の座標がセットされ、z成分には $P$ から $R$ までの距離 $s$ がセットされる ($P$ から $R$ までの距離は返されるが、$Q$ から $R$ までの距離は返されない)。
16行目以降は detA が $0$ の場合である。detA、すなわち $|A|$ が $0$ であるとは2つの単位ベクトル $\overrightarrow{\boldsymbol{a}} (a_x, a_y)$、$\overrightarrow{\boldsymbol{b}} (b_x, b_y)$ が平行であることを意味する。実際、ここで使われている行列 $A$ は具体的には $A = \begin{pmatrix}a_x &-b_x \\a_y &-b_y\end{pmatrix} $ であるが、上記の公式 $(2)$ より $|A| = -a_x b_y + b_x a_y$ となる。
したがって、$|A|=0$ ならば $b_x a_y = a_x b_y$、すなわち
\[\frac{a_y}{a_x} = \frac{b_y}{b_x} \]である。
これは 2つの直線の傾きが同じ、つまり 2つの直線が平行であることを意味している。
本来 平面上における2直線が平行である場合には下図32に示されるように、この2直線は交点を持たない。このような場合、このメソッドは Vector3.positiveInfinity を返す (25行目)。
しかし、2つの直線が平行であっても交点が存在する場合がある。それは図33に示されるように2つの直線が完全に重なってしまう場合である。図33のケースでは2直線の方向 $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ だけでなく $P$ と $Q$ を結ぶベクトル $\overrightarrow{W}$ も $\overrightarrow{\boldsymbol{a}}$、$\overrightarrow{\boldsymbol{b}}$ に対して平行となる。このようなケースは特別な場合として $P$ と $Q$ の中間点を交点 $R$ とし、この中間点を返すようにしている。18行目のifブロックはこの処理のためのものである (IsParallel_BOOL(..) は引数にセットされた2つのベクトルが平行であればtrueを返す)。
では上で述べてきたことを実際のプログラムで実装する。
# Code1
最初のプログラムは軸平行な長方形とレイとの衝突判定である。プログラム実行中にレイ及び長方形を動かすために、以下のキー操作を使用する。
H, J, K, L : 長方形を上下左右に動かす。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムを以下に示す (プログラム中では長方形は Rect という名前で使われている)。
[Code1] (実行結果 図34)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L))
{
MoveRect();
}
if (Input.GetKey(KeyCode.E))
{
ChangeRayDirection();
}
Vector2 v = GetRayDirection();
THMatrix3x3 M = Rect.GetMatrix();
Vector2 min = M * TH2DMath.ToVector3(c_initMinMax[0]);
Vector2 max = M * TH2DMath.ToVector3(c_initMinMax[1]);
Vector2[] res = CollisionTest_Ray_AABB(R0, v, new Vector2[] { min, max });
Hit(res);
14~16行目はその時点における長方形の左下隅、右上隅の頂点の計算であり、c_initMinMax は初期状態における長方形の左下隅、右上隅の頂点がセットされた配列である (初期状態では長方形は上図1のように中心が原点に置かれた軸平行な長方形であるので左下隅、右上隅の頂点は $(-w/2,-h/2)$、$(w/2,\ h/2)$ である)。
このプログラムでは長方形は軸平行な長方形であるので使われている衝突判定メソッドは CollisionTest_Ray_AABB(..) である (18行目)。レイと長方形が衝突している場合には、その衝突点が表示されるように衝突点がセットされた配列を補助メソッド Hit(..) にセットしている。
# Code2
次のプログラムはレイと一般の長方形との衝突判定であり、今回は回転している長方形も対象とする。キー操作はCode1とほとんど同じであるが、回転用のキーが追加されている。H, J, K, L : 長方形を上下左右に動かす。
R : 長方形を反時計周りに回転させる (Shiftと同時押しで時計周りに回転)。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムを以下に示す。
[Code2] (実行結果 図35)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L) ||
Input.GetKey(KeyCode.R))
{
MoveRect();
}
if (Input.GetKey(KeyCode.E))
{
ChangeRayDirection();
}
Vector2 v = GetRayDirection();
THMatrix3x3 M = Rect.GetMatrix();
Vector2 ui = M.GetColumn(0);
Vector2 uj = M.GetColumn(1);
Vector2 T = Rect.GetPosition();
Vector2[] res = CollisionTest_Ray_Rect(R0, v, T, ui, uj, c_RectW, c_RectH);
Hit(res);
T (18行目)はその時点での長方形の中心位置である。
このプログラムもCode1と同じくレイと長方形の間に衝突があれば、その衝突点を表示するだけである。今回は長方形が回転している場合も対象とするので衝突判定メソッドは CollisitonTest_Ray_Rect(..) が使われている (20行目 ; 引数に使われている c_RectW、c_RectH は長方形の横の辺、縦の辺の長さを表す定数)。
# Code3
続いてはレイと円盤の衝突判定である。図36はここで使用する円盤オブジェクト Disk の初期状態であり、初期状態では中心が原点に置かれており半径は $1$ である。プログラム中ではDiskの半径を適当な大きさに拡大している。 実行中にDisk及びレイを動かすには以下のキー操作を使用する。
H, J, K, L : Diskを上下左右に動かす。
E : レイを反時計周りに回転 (Shiftと同時押しで時計周りに回転)。
プログラムは次のとおり。
[Code3] (実行結果 図37)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L) )
{
MoveDisk();
}
if (Input.GetKey(KeyCode.E))
{
ChangeRayDirection();
}
Vector2 v = GetRayDirection();
Vector2 C = Disk.GetPosition();
float r = Disk.transform.localScale.x;
Vector2[] res = CollisionTest_Ray_Disk(R0, v, C, r);
Hit(res);
14行目の GetPosition() によって現時点でのDiskの中心が返される。15行目の transform.localScale.x はDiskに実行されている(x軸方向の)スケール倍率を表すが、初期状態でのDiskの半径は $1$ なのでこの値は現時点でのDiskの半径に相当する。
レイとDiskとの衝突点を求めるには、レイの始点 R0、方向 v、Diskの中心 C、半径 r を上で解説した CollisitonTest_Ray_Disk(..) にセットすればよい。
# Code4
最後は2つの直線同士の衝突判定である。ここでは2つの直線を動かすために以下のキー操作を使用する。H, J : 左側の直線を回転させる。
K, L : 右側の直線を回転させる。
プログラムは次のとおり。
[Code3] (実行結果 図38)
if (Input.GetKey(KeyCode.H) || Input.GetKey(KeyCode.J) ||
Input.GetKey(KeyCode.K) || Input.GetKey(KeyCode.L))
{
RotateLine();
}
Vector2 v1 = GetDirection_v1();
Vector2 v2 = GetDirection_v2();
Vector3 T = CalcIntersectionOf2Lines(P1, v1, P2, v2);
if (T.z != float.PositiveInfinity)
{
Dot.SetPosition(T);
}
4行目の RotateLine() は2つの直線を回転させるメソッドであるが、具体的には H、J を押すと左側の直線が反時計周り、時計周りに回転し、K、L を押すと右側の直線が反時計周り、時計周りに回転する。
7、8行目の GetDirection_v#() は各直線の方向を取得するためのメソッドであり、現時点での緑の矢印の方向が返される (返される値は単位ベクトル)。
10行目の CalcIntersectionOf2Lines(..) は上で解説した2直線の交点を求めるメソッドであり、このメソッドに2直線の直線上の点 及び方向をセットすれば2直線の交点が返される (14行目の Dot は交点を表すオブジェクトで、図38における小さな赤い点)。
(参考資料)
https://www.scratchapixel.com/lessons/3d-basic-rendering/minimal-ray-tracer-rendering-simple-shapes/ray-box-intersection.html
https://education.siggraph.org/static/HyperGraph/raytrace/rtinter3.htm
© 2020-2024 Redpoll's 60 (All rights reserved)