Redpoll's 60
Home / 3Dプログラミング入門 / 第2章 $§$2-3
第2章 2D空間におけるオブジェクトの運動
$§$2-3 行列による変換の詳細 2
コンピューターグラフィックスにおいて描画されるオブジェクトは、複数のオブジェクトによる階層構造で表現されている場合が多い。今までに見てきたオブジェクトは、すべて単一のオブジェクトであり、他のオブジェクトとの間に階層関係(いわゆる親子関係)がないもののみを扱っていた。
階層関係にある複数のオブジェクトの一体化した運動は、2-5節から始めるが、本節ではその予習として2つのオブジェクトを一体化させた場合の運動について簡単に見ていく。2つのオブジェクトの一体化は階層関係の例として最も単純な例である。
本節で使用するオブジェクトは次の2つである。
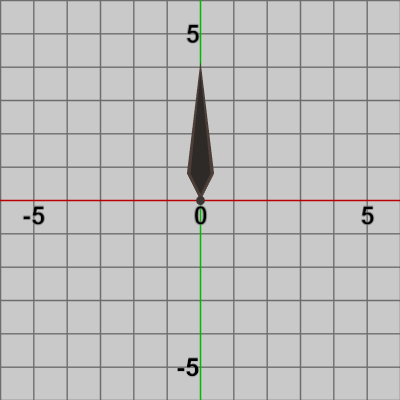
図1 Needle 初期状態 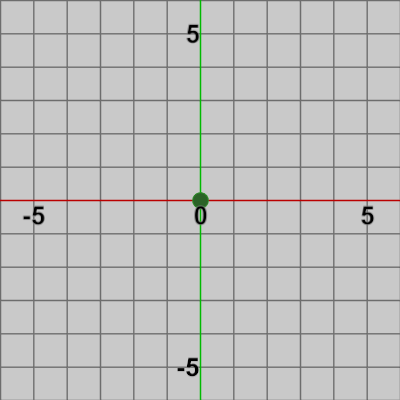
図2 Ball 初期状態
図はそれぞれの初期状態であり、図1では Needleの根元が原点に位置しており、図2では Ballの中心が原点に位置している (小さな緑色の円形オブジェクト)。
[Code1] (実行結果 図3)
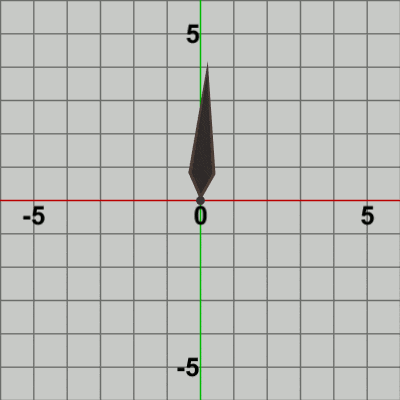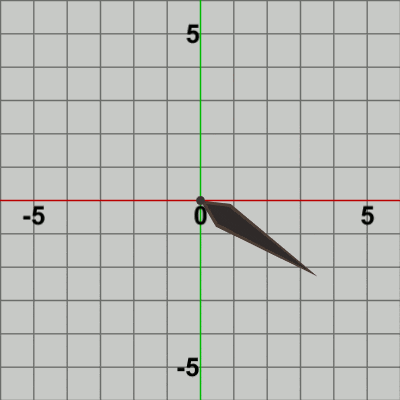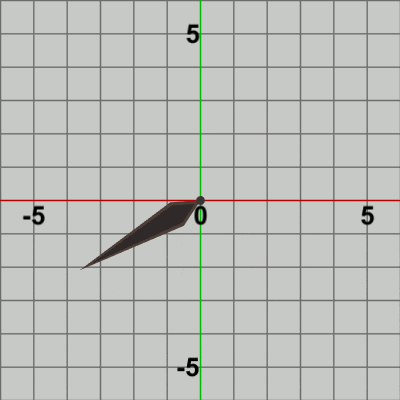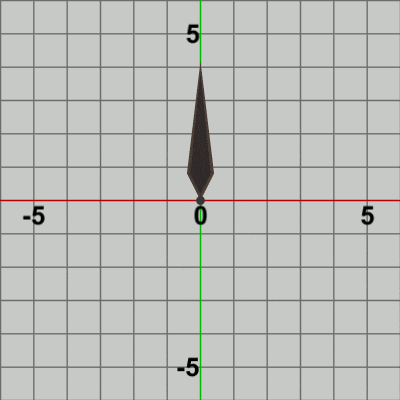
図3 Code1 実行結果 何度か述べているように、2D空間における回転は原点周りに行われる。したがって、Needleの根元を中心に Needleを回転させる場合には、Needleの根元が原点に位置している必要がある。ここでのNeedleは初期状態で根元が原点に置かれているので、その位置から移動させる必要はなく、そこで回転させればよい。
1行目の i_degNeedle は Needleの回転角度を表すインスタンス変数で、Needleが初期状態の向きから何度回転したかを表している。1-6節で述べたように、Unityの2D空間(XY平面)における回転は、反時計回りがプラス方向の回転である。したがって、時計回りに回転させるためには、毎フレーム マイナス方向に回転させる必要がある。1行目において i_degNeedle -= 3; と記述されているが、これは Needleが毎フレーム時計回りに$3$°ずつ回転することを意味している。2行目で計算される回転行列Rは i_degNeedleだけの回転を実行する行列であり、この行列を実行することによって Needleは初期状態の向き(図1に示されるようにy軸プラス側)から毎フレーム 角度i_degNeedleだけ回転することになるのである。
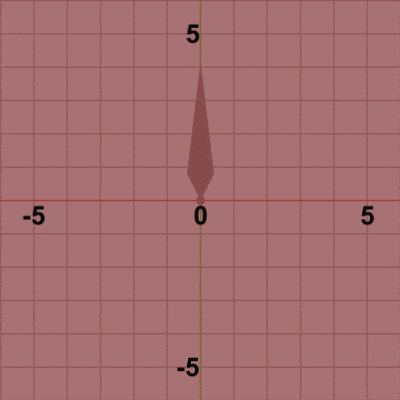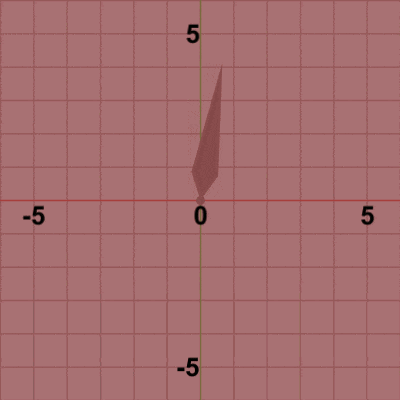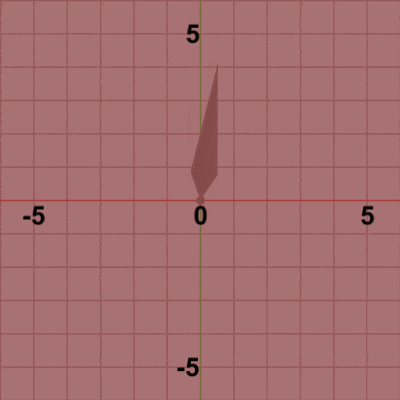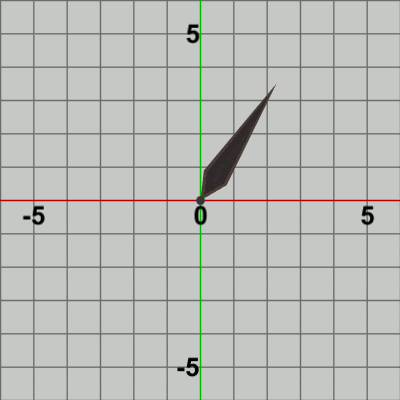
図4 図4は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターがかかっている状態は Needleに対して実行される変換行列Rの実行過程である。最初のフレームでは、初期状態の向きから$-3$°の回転が行われる。この回転が終わった時点で赤いフィルターの状態から通常の色に変化するが、この瞬間にフレーム描画が発生する。すなわち、通常色の状態は Needleに対する変換行列Rの実行結果である。前節でも述べたように、各フレームで描画されるのは初期状態のオブジェクトに対して変換行列を実行した結果の状態である。したがって、このプログラムにおける最初のフレームでは、Needleは初期状態の向きであるy軸プラス側から$-3$°回転した状態でフレーム描画が発生し、次のフレームでは初期状態の向きから$-6$°回転した状態でフレーム描画が発生する。さらにその次のフレームでは初期状態の向きから$-9$°回転した状態でフレーム描画が発生し、それ以降も同様に $-12$°, $-15$°, $-18$° ... と続いていく。
描画された各フレームを連続的に表示すれば図3のようなアニメーションになるというわけである。
まずは、原点周りの半径$1$の円周上での回転、すなわち 原点周りの公転を行うプログラムである。
[Beta2] (実行結果 図5)
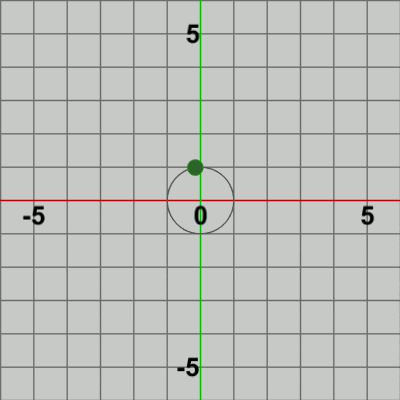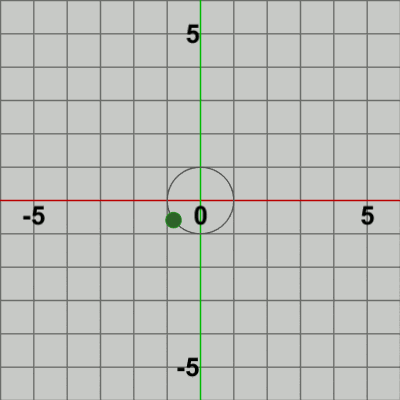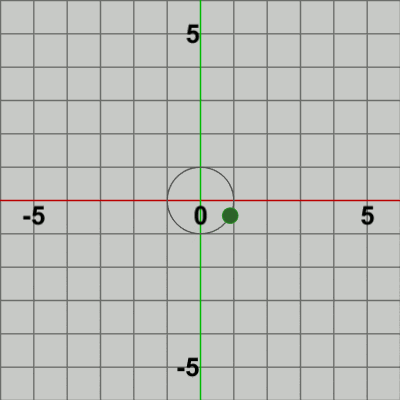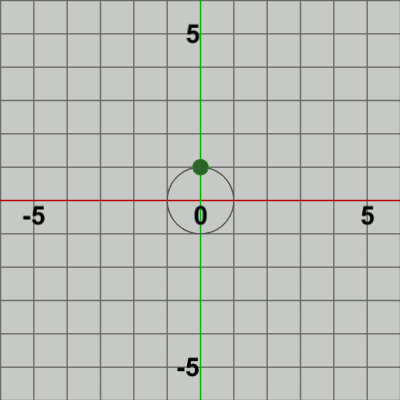
図5 Beta2 実行結果 1行目の i_revBallは、Ballの公転開始位置からの公転角度を表すインスタンス変数である。このインスタンス変数は、毎フレーム$9$ずつ加算されるが、これは すなわち、Ballの円周上での公転は毎フレーム$9$°ずつ反時計回りに行われることを意味している。2行目のRは角度i_revBallだけ回転させる回転行列であり、3行目のposには原点を中心とする半径$1$の円周上の位置が毎フレーム計算される。具体的には、Ballの公転は $(0, 1)$ を開始位置として始まるが、i_revBallはその開始位置から円周上を反時計回りに何度進んだかを表している。毎フレーム、この i_revBallを元にして円周上の位置posが計算され、その位置に Ballが移動することになる。
3行目の Vector3(0, 1, 1) は、Ballの公転開始位置$(0, 1)$を同次座標(1-5節参照)として表したものである。$3\times3$行列RとVector3(0, 1, 1)の積は本来は3次元ベクトル、すなわち Vector3型インスタンスとして返されるが、左辺のposはVector2型である。$3\times3$の回転行列と同次座標である3次元ベクトルの積のz成分は常に$1$であり(1-6節参照)、必要な情報は x、yの2つの成分のみである。第1章でも述べたが、Unityでは3行目のように Vector3型インスタンスをVector2型変数に代入する記述をすると、自動的にz成分が取り除かれてVector3の x、y成分のみがVector2にコピーされるのである。
5行目のTは、posだけの平行移動を実行する平行移動行列であり、毎フレーム6行目で このTを Ballに実行することで、Ballは初期状態の位置である原点から posだけ平行移動することになる。posは原点中心の半径$1$の円周上の位置であるため、Ballは毎フレーム円周上に移動するが、これによって Ballの運動が原点中心の半径$1$の円周上の公転となるわけである。
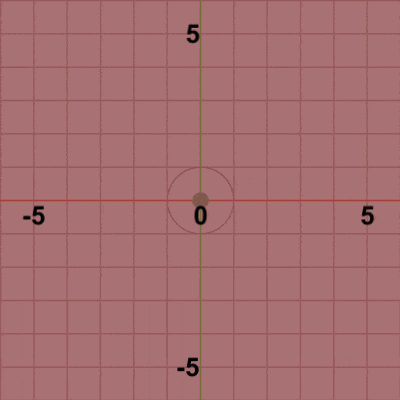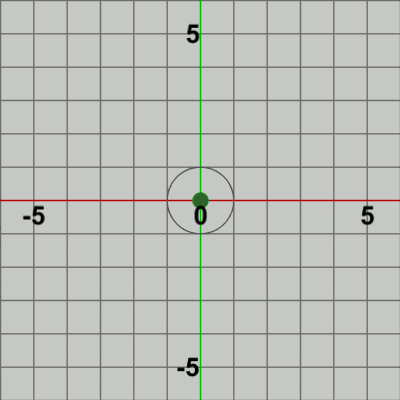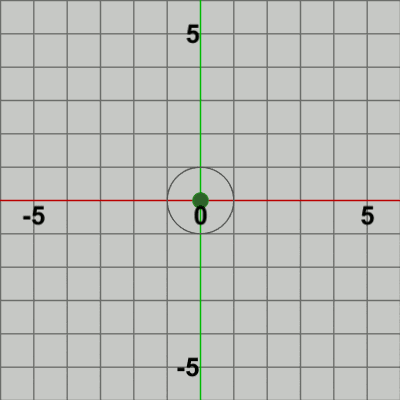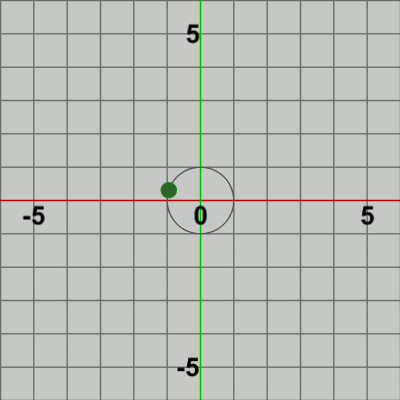
図6 図6は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターがかかっている状態は Ballに対して実行される変換行列Tの実行過程であり、通常色の状態は変換行列Tの実行結果の状態である。最初のフレームでは Ballは初期状態の位置である原点から公転開始位置の $(0, 1)$ へ移動し、その時点で通常色に変化するが、この瞬間においてフレーム描画が発生する。次のフレームでもBallは初期状態の位置から移動するが、その移動先は公転開始位置から$9$°回転した位置であり、その移動した位置においてフレーム描画が発生する。以降のフレームでも同様に、Ballは初期状態の位置から移動するが、その移動先は公転開始位置から$18$°回転した位置、$27$°回転した位置、$36$°回転した位置 ... と続き、その移動した位置においてフレーム描画が発生する。描画されたフレームを連続的に表示したものが図5のアニメーションである。
また、4行目のコメントアウトされている以下の記述は、
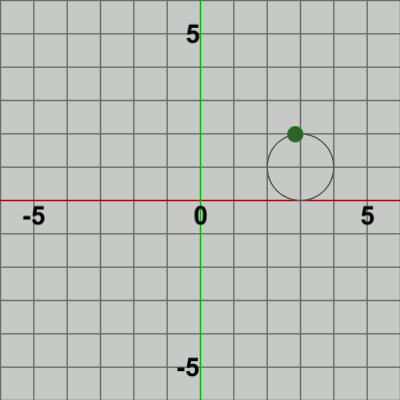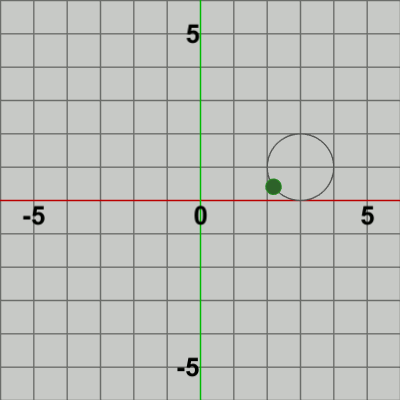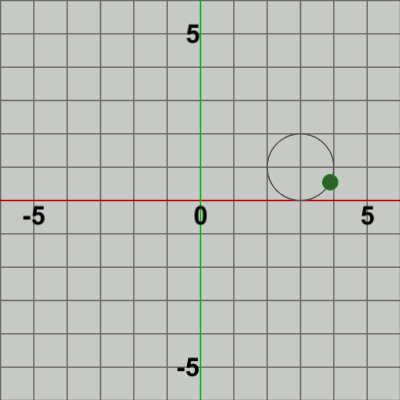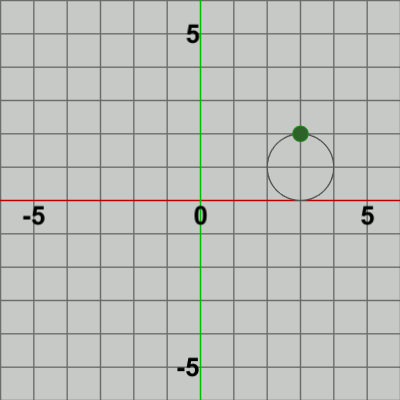
図7 Ballの公転軌道である半径$1$の円周を他の位置へ移動させるための処理である。Beta2の実行結果(図5)では、Ballの公転軌道の中心は原点である。この公転軌道の中心を他の位置にするためには、例えば $(a, b)$ 中心の半径$1$の円周上を公転させるようにするためには、毎フレームの Ballの移動先である 原点中心の半径$1$の円周上の各位置(posによって表される) を$(a, b)$だけずらせばよい。
具体的な例としては、Beta2の4行目の記述を有効にして、$(a, b) = (3, 1)$ とした場合の実行結果が図7である。このアニメーションでは、確かに Ballは $(3, 1)$中心の半径$1$の円周上を公転している。
目的とするプログラムは、Needleの先端を中心とする半径$1$の円周上での公転であった。Needle先端の座標は $(0, 4)$ であり(図1)、$(0, 4)$中心の半径$1$の円周上を公転軌道にするためには、Beta2の4行目を有効にして $(a, b) = (0, 4)$ とすればよい。
実際のプログラムを以下に示す。
[Code2] (実行結果 図8)
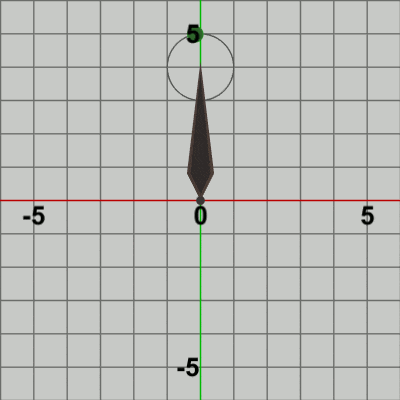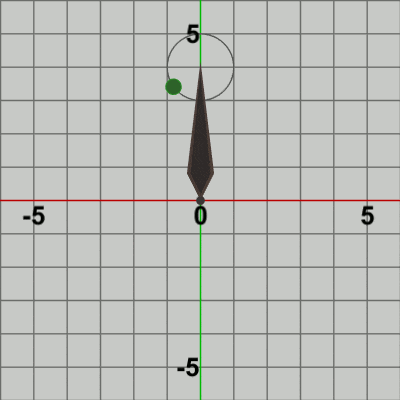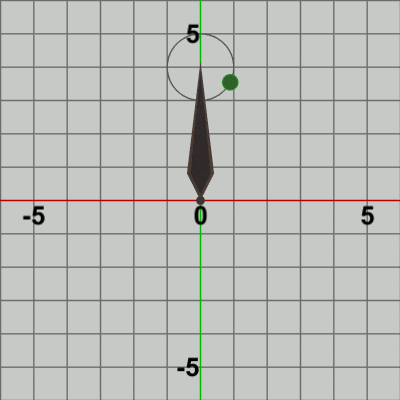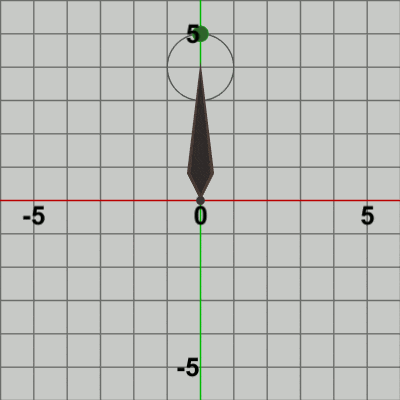
図8 Code2 実行結果 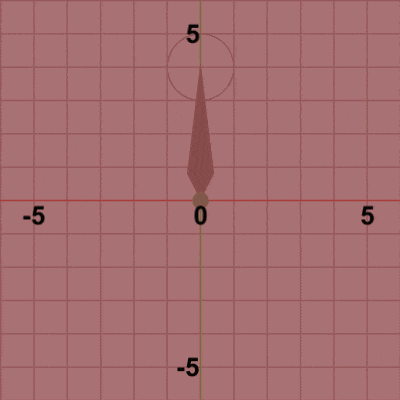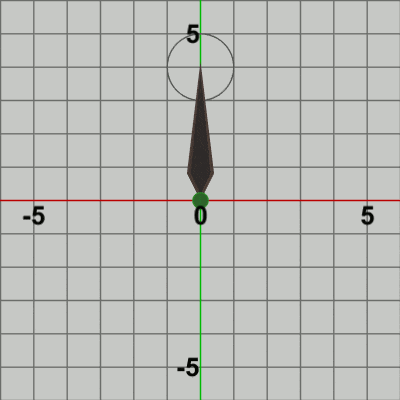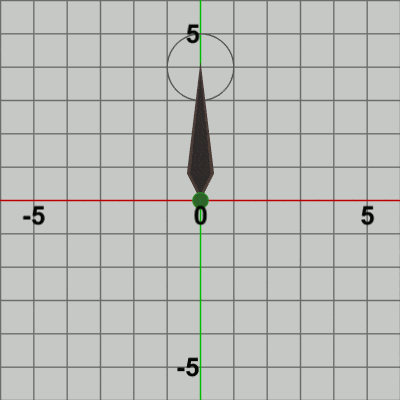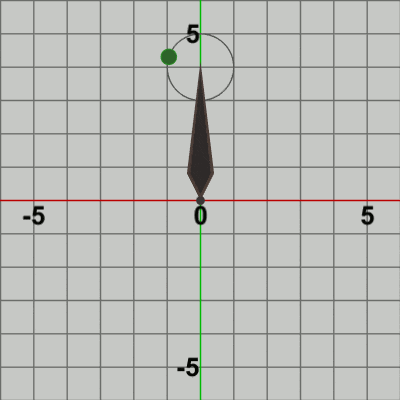
図9
図8は このプログラムの実行結果である。確かに、Needleの先端を中心とする半径$1$の円周上で Ballが公転をしている。Needleは初期状態から何も動かさないので、Needleに実行される行列は identity行列である。
図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態が、Ballに実行される変換行列Tの実行過程であり、通常色の状態が変換行列Tの実行結果の状態である。赤いフィルターの状態から通常色の状態に切り替わった瞬間にフレーム描画が発生する。描画されたフレームを連続的に表示すれば図8のアニメーションになる。
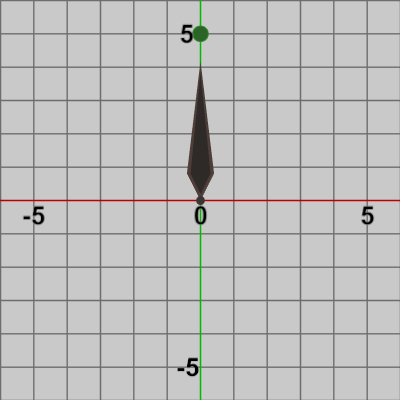
図10 BallをNeedleの先端から距離1だけ延長した位置に固定 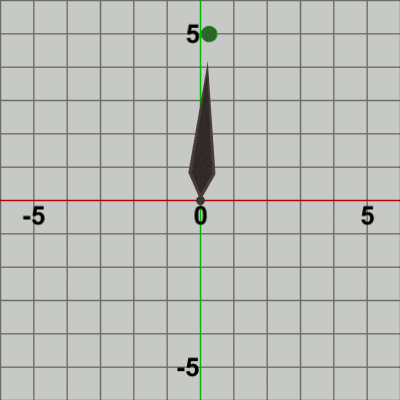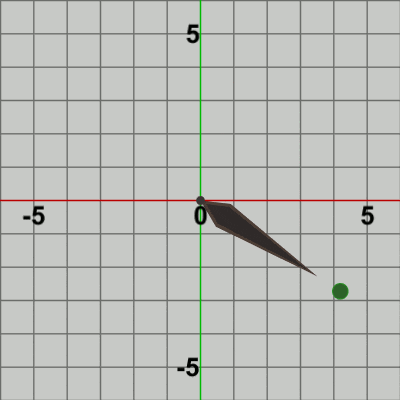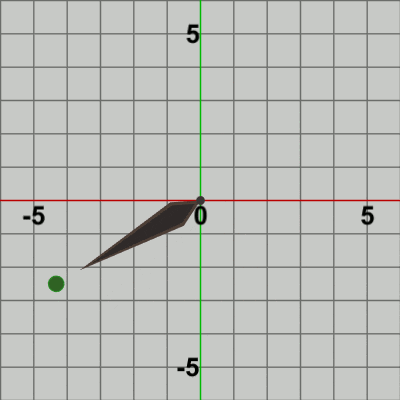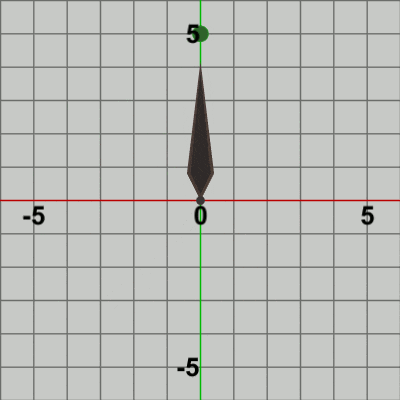
図11 Code3 実行結果 (Ballは常にNeedleの先端から距離1だけ延長した位置に固定されている)
[Code3] (実行結果 図11)
プログラム中の行列を表す変数には local や world といった接頭辞が付けられているが、ここでは形式的ものとして捉えて頂きたい。また、7行目などは単に他の変数に内容をコピーしているだけの冗長な処理であるが、これもまた形式的なものとして捉えて頂きたい。これらのことは学習を進めていく中で少しずつ解説していく。
1行目の localBallはBallを Needle先端の延長地点に移動させる平行移動行列である。localBallは毎フレーム、BallをNeedle先端の延長地点に移動させるだけの処理であり、その内容は毎フレーム同じものである (同じ内容の行列が毎フレーム計算される)。
4行目の localNeedleは Code1の回転行列Rと同じものであり、これは毎フレーム角度i_degNeedleだけ Needelを回転させる回転行列である (i_degNeedleは$3$ずつ減少する。これは 回転は時計回りに$3$°ずつの回転であることを意味する)。Needleに実行される行列 worldNeedleは localNeedleのコピーであり、これは Code1の回転行列Rと毎フレーム同じ内容であるから、Needleの運動は Code1の実行結果と変わらない。
ここで重要なのは、6行目の次のコードである。
Ballと Needleが一体となって運動するのはこの記述のためである。
worldBallは Ballに実行される行列であるが、その内容は、まず localBallが表す変換、次に localNeedleが表す変換をこの順序で実行するものである。具体的には、Needle先端の延長地点への平行移動、原点周りに角度i_degNeedleの回転 をこの順序で実行する。
図12は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。今までのプログラムでは、変換の実行対象のオブジェクトは1つであったが、ここでは2つのオブジェクトに対して変換を実行している。その際にも、実行される変換は初期状態のオブジェクトに対して実行される。言い換えれば、毎フレーム オブジェクトに実行される変換は、各オブジェクトの初期状態から始まる。この例では、毎フレーム Ballは初期状態の位置である原点から変換が始まり、Needleは初期状態の向きであるy軸プラス方向から変換が始まる。
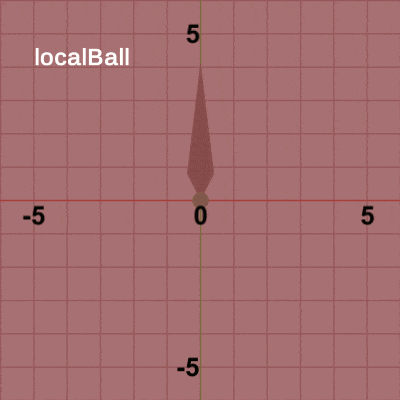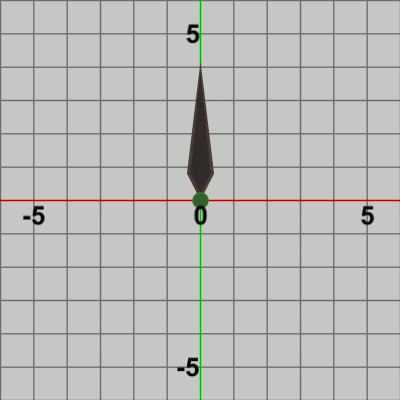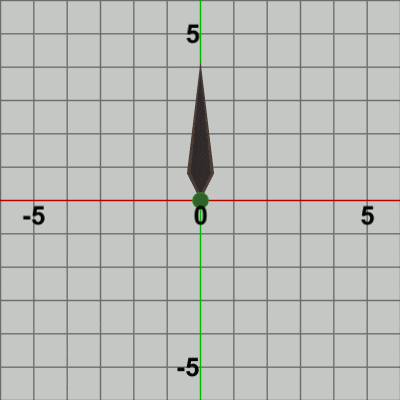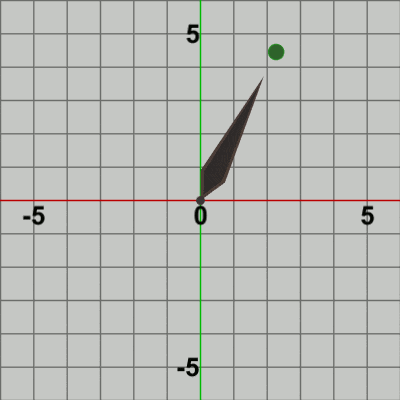
図12 赤いフィルターのかかっている状態は各オブジェクトに対して変換行列を実行している過程である。図12では白い文字で localBall、localNeedle といった単語が表示されるが、それらの単語が表示されているときには、それらの単語が表す変換行列を実行していることを意味している。つまり、localBallと表示されている状態は、localBallの実行過程を意味し、localNeedleと表示されている状態は、localNeedleの実行過程であることを意味している。
最初のフレームでは、まず Ballが Needle先端の延長地点に移動するが、この変換を表す行列が localBallである。Ballが延長地点に移動した時点で、次の変換が発生するが この変換が localNeedleである。localNeedleは、時計回りに角度i_degNeedleだけ回転させる回転行列であるが、最初のフレームでの回転角度は時計回りに$3$°である。localNeedleによって、Ballと Needleが一体となって時計回りに$3$°回転するが、それは Ballにも Needleにも localNeedleという同じ回転行列が実行されるためである。6行目、7行目の次のコードは、
Ball、Needleに実行される変換行列worldBall、worldNeedleの算出であるが、worldNeedleは localNeedleのコピーであるから その内容は localNeedleと変わらない。worldBallは、localBallと localNeedleの2つの変換をまとめたものであり、その実行結果は localBall、localNeedleをこの順序で実行した結果と同じである。重要なのは、Ballの場合は localBallを実行した後に localNeedleが実行されるということである。具体的には、localBallによって Needle先端の延長地点に移動するが、この移動した地点から localNeedleによる回転が実行される。これによって、Ballは Needleの延長地点に'固定'された状態で Needleと一体となって回転することになるのである。そして、Ball、Needleが時計回りに$3$°回転した時点で通常色に切り替わり、フレーム描画が発生する。
次のフレームでもオブジェクトに実行される変換は、それぞれの初期状態から始まる。まず、localBallによって Ballは初期状態の位置から Needle先端の延長地点に移動する。そして、localNeedleによる回転が実行されるが、この回転行列は Ball、Needleの両方に実行される。Ballの場合は延長地点から回転し、Needleの場合は初期状態の向きからの回転となる。回転角度は時計回りに$6$°であり、Ball、Needleが$6$°回転した時点で通常色に切り替わり、フレーム描画が発生する。それ以降のフレームにおいても、処理手順は同様である。
繰り返しになるが、Ballと Needleが一体となって運動するのは両者に同じ変換行列localNeedleが実行されるためである。そして、一体となって運動している間 Ballが常に Needle先端の延長地点に'固定'されているのは、Ballの場合は、最初の変換で Needle先端の延長地点へ移動する平行移動行列localBallを実行し、その後に localNeedleを実行するためである。localBallによって延長地点に移動し、そこで回転行列localNeedleが発生するので、その延長地点からの回転となり、結果的にその延長地点に'固定'されて Needleとともに回転するのである。
ここでは、Needleが回転している際に、Needleの先端を中心とする半径$1$の円周上を Ballが公転するプログラムを作成する。しかし、このプログラムを作成するにあたっては新しく考える部分はほとんどない。Code2、及び Code3を参考にすれば容易に目的の実装が得られる。
[Code4] (実行結果 図13)
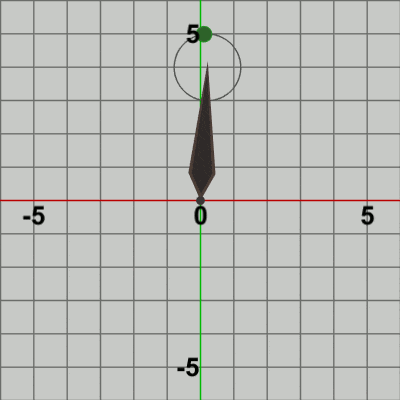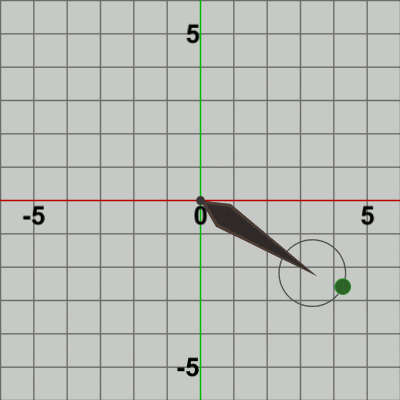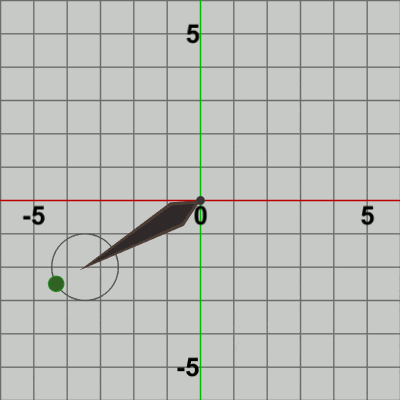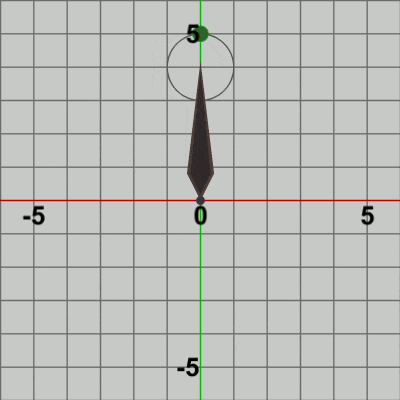
図13 Code4 実行結果 このプログラムは、1行目から5行目までは Code2と同じである (ただし1箇所、5行目の$3\times3$行列を表す変数名がここではlocalBallとなっている)。また、7行目以降は Code3の3行目以降と同じである。つまり、このプログラムはCode2とCode3を統合しただけのものである。
Code3では Ballは毎フレーム Needle先端の延長地点 $(0,\ 5)$ へ移動し、そこから毎フレーム Needleとともに回転が行われた。具体的には、Ballに最初に実行される変換行列localBallの内容は、毎フレーム 同じ位置$(0,\ 5)$への移動であり、その内容はプログラム実行中変わることはなかった。上でも解説したが、このために Code3の実行結果(図11)においては、Ballが Needleの延長地点で固定された状態で回転していたのである。
Needleの回転している際中に、Needle先端を中心とする半径$1$の円周上で Ballを公転させるためには、Ballに実行する最初の平行移動(localBall)において、その移動先を毎フレーム固定せずに公転軌道上の各位置に移動させればよいのである。
Code2で作成したプログラムは、Needleに変換を何も実行しない状態で、Ballが Needle先端を中心とする半径$1$の円周上を公転するというものであった(図8)。図9に示されるように、各フレームではBallが初期状態の位置から公転軌道上へ移動するが、Code2ではその後に特に変換は行われないので この時点でフレーム描画が発生する。Ballの公転角度i_revBallは毎フレーム $9$ずつ増加するので、描画されるフレームにおけるBallの位置は毎フレーム 公転軌道上を$9$°ずつ進んでいき、描画されたフレームを連続的に表示するとBallの公転として表示されるのであった。
つまり、Code2のように毎フレーム Ballを公転軌道上に移動させ、その移動が終わった後に、Code3のように Ballと Needleに対して localNeedleによる回転を実行する。これを毎フレーム繰り返していけば、Needleが回転している際中に、Needle先端を中心とする半径$1$の円周上で Ballが公転することになるわけである。

図12 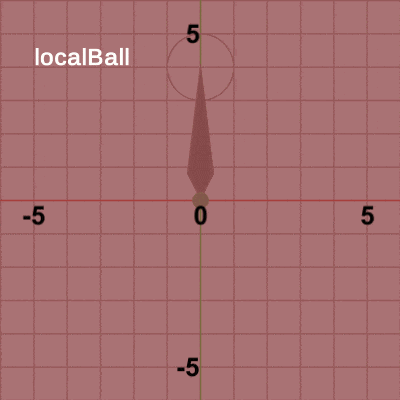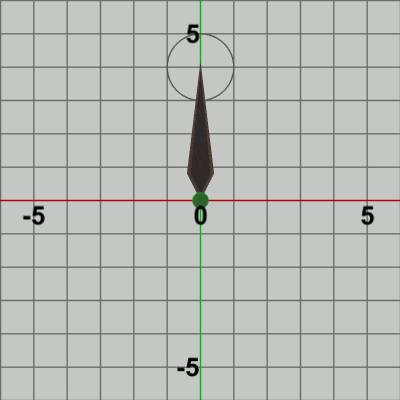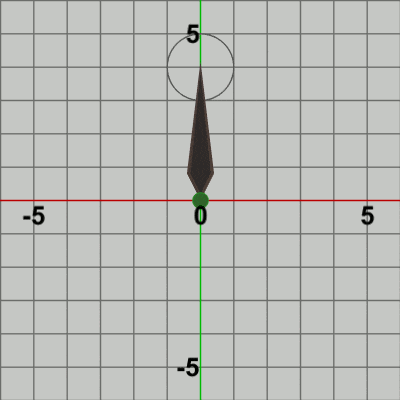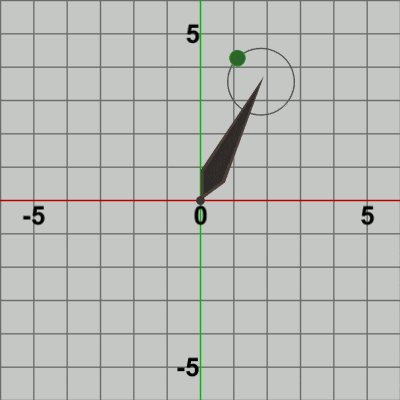
図14
図14は Code4の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。比較のために、先ほどの Code3のフレーム生成過程である図12を隣に表示している。
両者の違いは、Ballに実行される最初の変換 localBallの移動先だけであることが分かるであろう。図12の場合は、Ballは毎フレーム Needle先端の延長地点へ移動するのに対し、図14の場合は、Needle先端を中心とする半径$1$の円周上への移動となる。この違いによって Ballが Needle先端の延長地点で'固定'された状態で Needleとともに回転するか、あるいは、Needle先端を中心とする公転軌道上を公転するかという結果にわかれるのである (図11 及び 図13参照)。
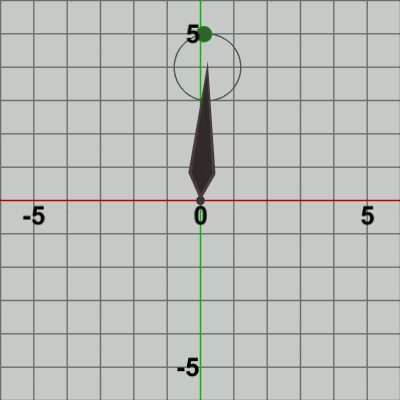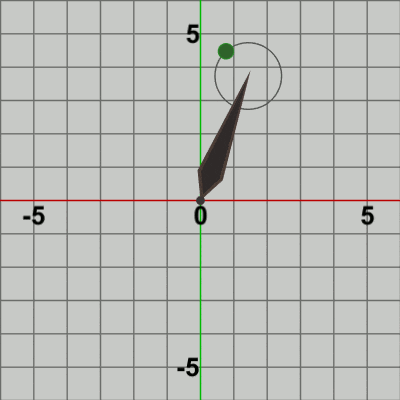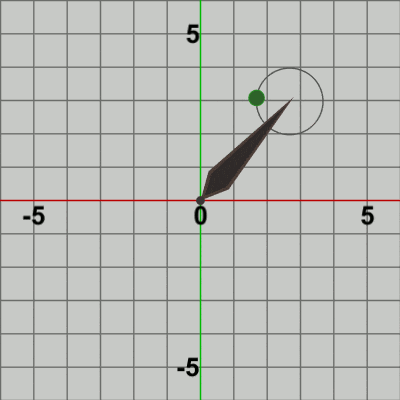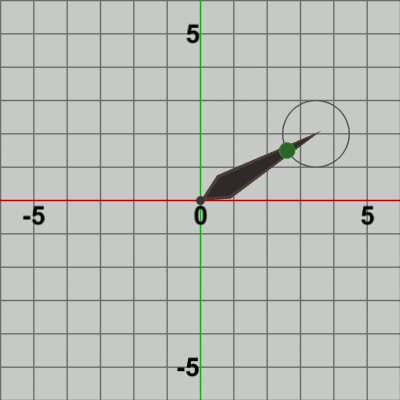
図15 図15は描画されたフレームのうち最初の20フレーム程をコマ送りで表示したものである (これらのフレームを連続的に表示したものが図13のアニメーションである)。
なお、前節でも指摘したがGPUでの描画において、描画されるのはオブジェクトに実行される変換行列の実行結果のみである。前節や本節において、一部のフレームに関して、オブジェクトに実行される変換をアニメーション化したものを使用している。そのアニメーションの中では、オブジェクトに実行される変換の実行過程が赤いフィルターのかかった状態で表示されているが、この実行過程の部分に関しては、この講義の解説目的で追加したものであって、実際のGPUにおけるフレーム描画にはこれらの過程は含まれない。あくまでフレーム描画の対象は変換の実行結果である。
前節、及び 本節ではオブジェクトに対して変換行列を実行することによってオブジェクトを運動させることについてやや詳しく見てきた。解説が長めになりはしたが、行列によってオブジェクトを動かすという考え方、いわば行列的な思考の導入部分としてはやむを得ないものなのである。ただし、3Dオブジェクトを運動させるにあたっても基本となるのは この行列的思考であり、考え方は2Dオブジェクトの場合と変わらない。そして、Unityにおける標準的な変換方法に関しても、その実体は行列による変換であり、基本となるのは行列的な思考なのである (これらのことについては第5章で解説する)。
階層関係にある複数のオブジェクトの一体化した運動は、2-5節から始めるが、本節ではその予習として2つのオブジェクトを一体化させた場合の運動について簡単に見ていく。2つのオブジェクトの一体化は階層関係の例として最も単純な例である。
本節で使用するオブジェクトは次の2つである。


図はそれぞれの初期状態であり、図1では Needleの根元が原点に位置しており、図2では Ballの中心が原点に位置している (小さな緑色の円形オブジェクト)。
# Code1
まず始めに、Needleが その根元を中心として時計回りに回転するプログラムを作成する。[Code1] (実行結果 図3)
i_degNeedle -= 3; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_degNeedle); Needle.SetMatrix(R);

1行目の i_degNeedle は Needleの回転角度を表すインスタンス変数で、Needleが初期状態の向きから何度回転したかを表している。1-6節で述べたように、Unityの2D空間(XY平面)における回転は、反時計回りがプラス方向の回転である。したがって、時計回りに回転させるためには、毎フレーム マイナス方向に回転させる必要がある。1行目において i_degNeedle -= 3; と記述されているが、これは Needleが毎フレーム時計回りに$3$°ずつ回転することを意味している。2行目で計算される回転行列Rは i_degNeedleだけの回転を実行する行列であり、この行列を実行することによって Needleは初期状態の向き(図1に示されるようにy軸プラス側)から毎フレーム 角度i_degNeedleだけ回転することになるのである。

描画された各フレームを連続的に表示すれば図3のようなアニメーションになるというわけである。
# Code2
では次に、Ballを Needleの先端を中心とする半径$1$の円周上で回転させるプログラムを作成する。まずは、原点周りの半径$1$の円周上での回転、すなわち 原点周りの公転を行うプログラムである。
[Beta2] (実行結果 図5)
i_revBall += 9; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_revBall); Vector2 pos = R * new Vector3(0, 1, 1); // pos += new Vector2(a, b); // 回転の中心を(a, b)に移動 THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); Ball.SetMatrix(T);

3行目の Vector3(0, 1, 1) は、Ballの公転開始位置$(0, 1)$を同次座標(1-5節参照)として表したものである。$3\times3$行列RとVector3(0, 1, 1)の積は本来は3次元ベクトル、すなわち Vector3型インスタンスとして返されるが、左辺のposはVector2型である。$3\times3$の回転行列と同次座標である3次元ベクトルの積のz成分は常に$1$であり(1-6節参照)、必要な情報は x、yの2つの成分のみである。第1章でも述べたが、Unityでは3行目のように Vector3型インスタンスをVector2型変数に代入する記述をすると、自動的にz成分が取り除かれてVector3の x、y成分のみがVector2にコピーされるのである。
5行目のTは、posだけの平行移動を実行する平行移動行列であり、毎フレーム6行目で このTを Ballに実行することで、Ballは初期状態の位置である原点から posだけ平行移動することになる。posは原点中心の半径$1$の円周上の位置であるため、Ballは毎フレーム円周上に移動するが、これによって Ballの運動が原点中心の半径$1$の円周上の公転となるわけである。

また、4行目のコメントアウトされている以下の記述は、
// pos += new Vector2(a, b); // 回転の中心を(a, b)に移動

具体的な例としては、Beta2の4行目の記述を有効にして、$(a, b) = (3, 1)$ とした場合の実行結果が図7である。このアニメーションでは、確かに Ballは $(3, 1)$中心の半径$1$の円周上を公転している。
目的とするプログラムは、Needleの先端を中心とする半径$1$の円周上での公転であった。Needle先端の座標は $(0, 4)$ であり(図1)、$(0, 4)$中心の半径$1$の円周上を公転軌道にするためには、Beta2の4行目を有効にして $(a, b) = (0, 4)$ とすればよい。
実際のプログラムを以下に示す。
[Code2] (実行結果 図8)
i_revBall += 9; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_revBall); Vector2 pos = R * new Vector3(0, 1, 1); pos += new Vector2(0, 4); THMatrix3x3 T = TH2DMath.GetTranslation3x3(pos); Ball.SetMatrix(T); Needle.SetMatrix(THMatrix3x3.identity);


図8は このプログラムの実行結果である。確かに、Needleの先端を中心とする半径$1$の円周上で Ballが公転をしている。Needleは初期状態から何も動かさないので、Needleに実行される行列は identity行列である。
図9は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。赤いフィルターのかかっている状態が、Ballに実行される変換行列Tの実行過程であり、通常色の状態が変換行列Tの実行結果の状態である。赤いフィルターの状態から通常色の状態に切り替わった瞬間にフレーム描画が発生する。描画されたフレームを連続的に表示すれば図8のアニメーションになる。
# Code3
続いて、Ballが Needleの先端から距離$1$だけ延長した位置(図10に示される位置 $(0, 5)$)に'固定'されている状態で、Needleに対して回転を実行する。「Needleの先端から距離$1$だけ延長した位置に固定されている状態」とは、Needleが回転している際中も Ballは、Needleの先端から距離$1$だけ延長した位置に置かれていることを意味する。具体的には、このプログラムの実行結果である図11のような状態である。図11では、Ballが Needle先端の延長地点に'固定'され、Needleの回転中も Needleと一体となって運動している。

[Code3] (実行結果 図11)
THMatrix3x3 localBall = TH2DMath.GetTranslation3x3(0, 5); i_degNeedle -= 3; THMatrix3x3 localNeedle = TH2DMath.GetRotation3x3(i_degNeedle); THMatrix3x3 worldBall = localNeedle * localBall; THMatrix3x3 worldNeedle = localNeedle; Ball.SetMatrix(worldBall); Needle.SetMatrix(worldNeedle);
プログラム中の行列を表す変数には local や world といった接頭辞が付けられているが、ここでは形式的ものとして捉えて頂きたい。また、7行目などは単に他の変数に内容をコピーしているだけの冗長な処理であるが、これもまた形式的なものとして捉えて頂きたい。これらのことは学習を進めていく中で少しずつ解説していく。
1行目の localBallはBallを Needle先端の延長地点に移動させる平行移動行列である。localBallは毎フレーム、BallをNeedle先端の延長地点に移動させるだけの処理であり、その内容は毎フレーム同じものである (同じ内容の行列が毎フレーム計算される)。
4行目の localNeedleは Code1の回転行列Rと同じものであり、これは毎フレーム角度i_degNeedleだけ Needelを回転させる回転行列である (i_degNeedleは$3$ずつ減少する。これは 回転は時計回りに$3$°ずつの回転であることを意味する)。Needleに実行される行列 worldNeedleは localNeedleのコピーであり、これは Code1の回転行列Rと毎フレーム同じ内容であるから、Needleの運動は Code1の実行結果と変わらない。
ここで重要なのは、6行目の次のコードである。
THMatrix3x3 worldBall = localNeedle * localBall;
worldBallは Ballに実行される行列であるが、その内容は、まず localBallが表す変換、次に localNeedleが表す変換をこの順序で実行するものである。具体的には、Needle先端の延長地点への平行移動、原点周りに角度i_degNeedleの回転 をこの順序で実行する。
図12は最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。今までのプログラムでは、変換の実行対象のオブジェクトは1つであったが、ここでは2つのオブジェクトに対して変換を実行している。その際にも、実行される変換は初期状態のオブジェクトに対して実行される。言い換えれば、毎フレーム オブジェクトに実行される変換は、各オブジェクトの初期状態から始まる。この例では、毎フレーム Ballは初期状態の位置である原点から変換が始まり、Needleは初期状態の向きであるy軸プラス方向から変換が始まる。

最初のフレームでは、まず Ballが Needle先端の延長地点に移動するが、この変換を表す行列が localBallである。Ballが延長地点に移動した時点で、次の変換が発生するが この変換が localNeedleである。localNeedleは、時計回りに角度i_degNeedleだけ回転させる回転行列であるが、最初のフレームでの回転角度は時計回りに$3$°である。localNeedleによって、Ballと Needleが一体となって時計回りに$3$°回転するが、それは Ballにも Needleにも localNeedleという同じ回転行列が実行されるためである。6行目、7行目の次のコードは、
THMatrix3x3 worldBall = localNeedle * localBall; THMatrix3x3 worldNeedle = localNeedle;
次のフレームでもオブジェクトに実行される変換は、それぞれの初期状態から始まる。まず、localBallによって Ballは初期状態の位置から Needle先端の延長地点に移動する。そして、localNeedleによる回転が実行されるが、この回転行列は Ball、Needleの両方に実行される。Ballの場合は延長地点から回転し、Needleの場合は初期状態の向きからの回転となる。回転角度は時計回りに$6$°であり、Ball、Needleが$6$°回転した時点で通常色に切り替わり、フレーム描画が発生する。それ以降のフレームにおいても、処理手順は同様である。
繰り返しになるが、Ballと Needleが一体となって運動するのは両者に同じ変換行列localNeedleが実行されるためである。そして、一体となって運動している間 Ballが常に Needle先端の延長地点に'固定'されているのは、Ballの場合は、最初の変換で Needle先端の延長地点へ移動する平行移動行列localBallを実行し、その後に localNeedleを実行するためである。localBallによって延長地点に移動し、そこで回転行列localNeedleが発生するので、その延長地点からの回転となり、結果的にその延長地点に'固定'されて Needleとともに回転するのである。
# Code4
Code3では Ballと Needleの一体化した運動を扱ったが、そこでは Ballは常に Needle先端の延長地点に'固定'されたままであり、その延長地点から Ballは一切動くことはなかった。ここでは、Needleが回転している際に、Needleの先端を中心とする半径$1$の円周上を Ballが公転するプログラムを作成する。しかし、このプログラムを作成するにあたっては新しく考える部分はほとんどない。Code2、及び Code3を参考にすれば容易に目的の実装が得られる。
[Code4] (実行結果 図13)
i_revBall += 9; THMatrix3x3 R = TH2DMath.GetRotation3x3(i_revBall); Vector2 pos = R * new Vector3(0, 1, 1); pos += new Vector2(0, 4); THMatrix3x3 localBall = TH2DMath.GetTranslation3x3(pos); i_degNeedle -= 3; THMatrix3x3 localNeedle = TH2DMath.GetRotation3x3(i_degNeedle); THMatrix3x3 worldBall = localNeedle * localBall; THMatrix3x3 worldNeedle = localNeedle; Ball.SetMatrix(worldBall); Needle.SetMatrix(worldNeedle);

Code3では Ballは毎フレーム Needle先端の延長地点 $(0,\ 5)$ へ移動し、そこから毎フレーム Needleとともに回転が行われた。具体的には、Ballに最初に実行される変換行列localBallの内容は、毎フレーム 同じ位置$(0,\ 5)$への移動であり、その内容はプログラム実行中変わることはなかった。上でも解説したが、このために Code3の実行結果(図11)においては、Ballが Needleの延長地点で固定された状態で回転していたのである。
Needleの回転している際中に、Needle先端を中心とする半径$1$の円周上で Ballを公転させるためには、Ballに実行する最初の平行移動(localBall)において、その移動先を毎フレーム固定せずに公転軌道上の各位置に移動させればよいのである。
Code2で作成したプログラムは、Needleに変換を何も実行しない状態で、Ballが Needle先端を中心とする半径$1$の円周上を公転するというものであった(図8)。図9に示されるように、各フレームではBallが初期状態の位置から公転軌道上へ移動するが、Code2ではその後に特に変換は行われないので この時点でフレーム描画が発生する。Ballの公転角度i_revBallは毎フレーム $9$ずつ増加するので、描画されるフレームにおけるBallの位置は毎フレーム 公転軌道上を$9$°ずつ進んでいき、描画されたフレームを連続的に表示するとBallの公転として表示されるのであった。
つまり、Code2のように毎フレーム Ballを公転軌道上に移動させ、その移動が終わった後に、Code3のように Ballと Needleに対して localNeedleによる回転を実行する。これを毎フレーム繰り返していけば、Needleが回転している際中に、Needle先端を中心とする半径$1$の円周上で Ballが公転することになるわけである。


図14は Code4の最初のいくつかのフレームにおいて、オブジェクトに実行される変換をアニメーションとして表したものである。比較のために、先ほどの Code3のフレーム生成過程である図12を隣に表示している。
両者の違いは、Ballに実行される最初の変換 localBallの移動先だけであることが分かるであろう。図12の場合は、Ballは毎フレーム Needle先端の延長地点へ移動するのに対し、図14の場合は、Needle先端を中心とする半径$1$の円周上への移動となる。この違いによって Ballが Needle先端の延長地点で'固定'された状態で Needleとともに回転するか、あるいは、Needle先端を中心とする公転軌道上を公転するかという結果にわかれるのである (図11 及び 図13参照)。

なお、前節でも指摘したがGPUでの描画において、描画されるのはオブジェクトに実行される変換行列の実行結果のみである。前節や本節において、一部のフレームに関して、オブジェクトに実行される変換をアニメーション化したものを使用している。そのアニメーションの中では、オブジェクトに実行される変換の実行過程が赤いフィルターのかかった状態で表示されているが、この実行過程の部分に関しては、この講義の解説目的で追加したものであって、実際のGPUにおけるフレーム描画にはこれらの過程は含まれない。あくまでフレーム描画の対象は変換の実行結果である。
前節、及び 本節ではオブジェクトに対して変換行列を実行することによってオブジェクトを運動させることについてやや詳しく見てきた。解説が長めになりはしたが、行列によってオブジェクトを動かすという考え方、いわば行列的な思考の導入部分としてはやむを得ないものなのである。ただし、3Dオブジェクトを運動させるにあたっても基本となるのは この行列的思考であり、考え方は2Dオブジェクトの場合と変わらない。そして、Unityにおける標準的な変換方法に関しても、その実体は行列による変換であり、基本となるのは行列的な思考なのである (これらのことについては第5章で解説する)。
© 2020-2025 Redpoll's 60 (All rights reserved)