Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-4
第3章 3D空間の基礎
$§$3-4 ベクトルの内積
ベクトルの内積は 2D空間の章では 2-20節、2-21節の衝突判定において使われたが、これ以降の3D空間の章においてもベクトルの内積は頻繁に使用される。本節では3D版の内積の基礎及び、いくつかの使用例について見ていくが、その内容は2D版の内積の復習のようなものである。
ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$の内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2\]
(計算例)
ベクトル$\boldsymbol{\mathsf{v_1}} = (1, 2, 3)$と $\boldsymbol{\mathsf{v_2}} = (6, 5, 4)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 1\cdot6 + 2\cdot5 + 3\cdot4 = 6 + 10 + 12 = 28\] ベクトル$\boldsymbol{\mathsf{v_1}} = (3, -1, -5)$と $\boldsymbol{\mathsf{v_2}} = (0,\ 5, -1)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 3\cdot0 + (-1)\cdot5 + (-5)\cdot(-1) = 0 + (-5) + 5 = 0\]
定義から明らかなように、内積は以下のように積の順序について交換可能である。
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = \boldsymbol{\mathsf{v_2}}\cdot\boldsymbol{\mathsf{v_1}}\]
また、同じベクトル同士の内積、例えばベクトル$\boldsymbol{\mathsf{v}} = (x, y, z)$同士の内積は、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = xx + yy + zz = x^2 + y^2 + z^2\] となるが、これはベクトル$\boldsymbol{\mathsf{v}}$の大きさ($|\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}$)の$2$乗に等しい。すなわち、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = |\boldsymbol{\mathsf{v}}|^2\] である。
ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$のなす角を $A$とし、$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の大きさを$|\boldsymbol{\mathsf{v_1}}|$、$|\boldsymbol{\mathsf{v_2}}|$とすれば
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2 = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\cos{A}\] である。
図1のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$は、両者のなす角が $A$である。図2は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である(両者のなす角は変わらない)。
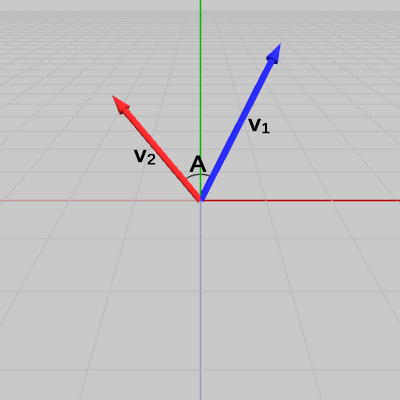
図1 ベクトルv1、v2 (両者のなす角はA) 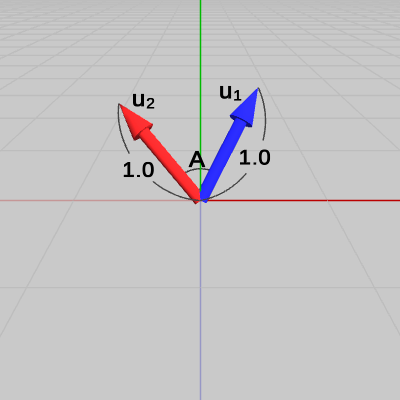
図2 ベクトルv1、v2を正規化したu1、u2
上の等式における$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の代わりに単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$を式に使った場合、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = |\boldsymbol{u_1}||\boldsymbol{u_2}|\cos{A} \] となるが、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$は単位ベクトルであるから、$|\boldsymbol{u_1}|$、$|\boldsymbol{u_2}|$の値は$1$である。すなわち、\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} \] が成り立つ。
この結果は、2つのベクトルの単位ベクトルの内積を求めれば、その2つのベクトルのなす角を知ることが可能であることを意味している。
以下では、その特殊な例として2つのベクトルが直交している場合、あるいは平行である場合の判定方法について見ていく。
(注) 以下の例ではベクトルのなす角は、0°~180°の範囲にあるものとする。
(例1) 2つのベクトルが直交しているかどうかの判定(なす角が$90$°)
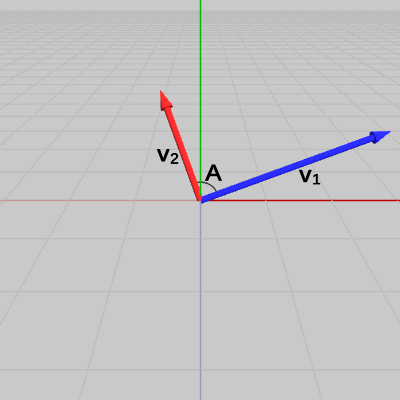
図3 ベクトルv1、v2 (両者のなす角はA) 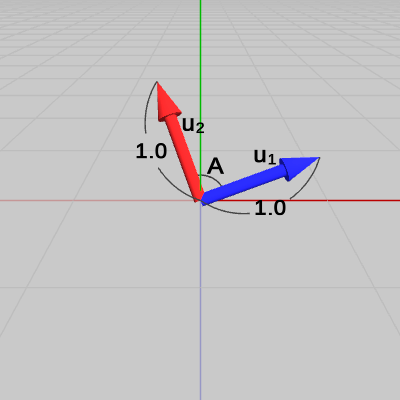
図4 ベクトルv1、v2を正規化したu1、u2
図3に示されるベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$のなす角を $A$とする。図4は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0\] 上で述べたように、単位ベクトルの内積はそれらのなす角の余弦($\cos$)に等しいから、結局\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 0\] となる。
$\cos{A} = 0$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 90$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$0$になる場合では、両者は直交していることがわかる(2つのベクトルが直交している場合は、両者を正規化せずに内積を計算しても結果は$0$になる。つまり、この例では$\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$の値も$0$である)。
(例2) 2つのベクトルが平行であるかどうかの判定 1 (なす角が$0$°)
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図5に示される位置に置かれている。この2つのベクトルのなす角は、両者の始点を原点に移動させたときの2つのベクトルのなす角のことである。今回の例では、2つのベクトルを原点に移動させたときに(図6)、2つのベクトルが重なってしまっているので角度の表示がされていないが、ここでも両者のなす角を$A$とする。
図7は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1\] 先程と同じように、両者のなす角の余弦($\cos$)を使って表せば、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 1\] となる。
$\cos{A} = 1$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 0$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$1$になる場合では、両者は平行でありベクトルの向きも同じであることがわかる。
(例3) 2つのベクトルが平行であるかどうかの判定 2 (なす角が$180$°)
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図8に示される位置に置かれている。この2つのベクトルのなす角は、上の例で述べたように両者の始点を原点に移動させたときの2つのベクトルのなす角のことであり、図9に示されるようにここでも両者のなす角を$A$とする。
図10は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = -1\] $\cos{A} = -1$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 180$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$-1$になる場合では、両者は平行であるがベクトルの向きは逆向きであることがわかる。
以上をまとめると、2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ 及び、それらの単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積について次のことがいえる。
(ⅰ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0$ のとき、2つのベクトルは直交する。
(ⅱ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1$ のとき、2つのベクトルは平行であり同じ向きである。
(ⅲ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = -1$ のとき、2つのベクトルは平行であり逆向きである。
ここではベクトルのなす角の範囲を$0$°~$180$°の範囲に制限したが、この範囲を$0$°より下、あるいは$180$°より上の範囲に広げても上記の(ⅰ)~(ⅲ)は成立する。
ベクトル $\boldsymbol{\mathsf{v}}$ を単位ベクトルとし、$\boldsymbol{\mathsf{v}}$ をXZ平面上へ射影したベクトルを $\boldsymbol{\mathsf{v}}'$ とする (下図F1)。また y軸とのなす角を $\theta$、$\boldsymbol{\mathsf{v}}'$ と x軸とのなす角を $\varphi$ とし、それぞれの角度の範囲を $0 \leq \theta \leq \pi$、$-\pi \leq \varphi \leq \pi$ とする ($\theta$、$\varphi$ がこの範囲であれば、$\boldsymbol{\mathsf{v}}$ を3D空間内の任意の方向に向けることができる)。
単位ベクトル $\boldsymbol{\mathsf{v}}$ が初期状態において y軸プラス方向をむいていたとして、$\boldsymbol{\mathsf{v}}$ を y軸プラス方向から左図の状態にするための角度 $\theta$、$\varphi$ を求めることについて考えよう。
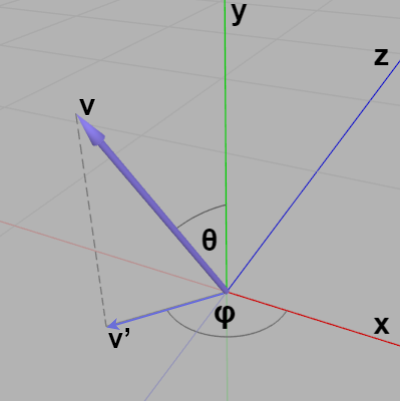
図F1 単位ベクトル $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}$ をXZ平面上に射影したベクトル $\boldsymbol{\mathsf{v}}'$ 
図F2 $\boldsymbol{\mathsf{v}}$ の初期状態
$\theta$ の求め方は簡単である。$\theta$ は $\boldsymbol{\mathsf{v}}$ と y軸のなす角であるから、$\boldsymbol{\mathsf{v}} = (\mathsf{v_x},\ \mathsf{v_y},\ \mathsf{v_z})$、$\boldsymbol{y} = (0, 1, 0)$ とすれば、\[ \boldsymbol{\mathsf{v}}\cdot \boldsymbol{y} = \mathsf{v_y} = \cos\theta \]である。したがって $\cos$ の逆関数 $\arccos$ を使って、$\theta = \arccos(\mathsf{v_y})$ とすればよい ($\arccos$ の引数は $-1$ ~ $1$ の範囲でなければならない。算出される角度の範囲は $0$ ~ $\pi$ である)。
プログラムにすれば以下のように記述される。
Unityに用意されている $\arccos$ は Mathf 構造体の Acos(..) であり、戻り値は $0$ ~ $\pi$ のラジアンで返される。そのため度数法の角度に変換する際は3行目のように Rad2Deg を掛ける必要がある (Rad2Deg の実際の値は $180/\pi$ )。
ただし回転角度を考える場合には注意が1つ必要である。それはどの軸を回転軸にするかによって回転角度の符号が変わるためである。
例えば上で求めた角度 $\theta$ を z軸周りの回転で使うとしよう。その場合、前節で述べたように z軸プラス方向に(左手の)親指を向けたときの残りの指の曲がっている方向が回転角度の増加方向である。したがって、$\boldsymbol{\mathsf{v}}$ を下図F3のように回転させるには z軸周りに $-\theta$ 回転させる必要があるということである ($0 \leq \theta \leq \pi$ に制限していたから $\theta$ は必ず $0$ 以上の正の値)。

図F3 z軸周りの $-\theta$ の回転 ($0 \leq \theta \leq \pi$) 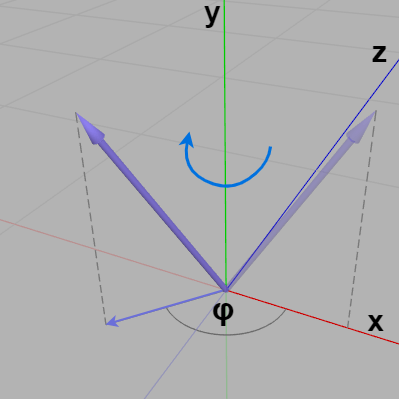
図F4 y軸周りの $\varphi$ の回転 ($-\pi \leq \varphi \leq \pi$)
$\boldsymbol{\mathsf{v}}$ を z軸周りに $-\theta$ 回転させた時点では $\boldsymbol{\mathsf{v}}$ はXY平面上にある。$\boldsymbol{\mathsf{v}}$ を目的の方向に向けるには、さらに y軸周りの $\varphi$ の回転を行う必要がある (図F4)。
$\varphi$ は $\boldsymbol{\mathsf{v}}$ をXZ平面上に射影したベクトル $\boldsymbol{\mathsf{v}}'$ と x軸とのなす角であるから、$\boldsymbol{\mathsf{v}}'$ と x軸の内積から上記と同じく $\arccos$ を使って求めることはできる。しかし x軸とのなす角が $\varphi$ ではなく $-\varphi$ であるようなベクトルを $\boldsymbol{\mathsf{w}}$ とすれば、$\boldsymbol{\mathsf{w}}$ と x軸とのなす角は $-\varphi$ であるから、x軸との内積を計算する場合 $\boldsymbol{\mathsf{v}}'$ でも $\boldsymbol{\mathsf{w}}$ でも内積は同じになってしまう。
つまり x軸を表す単位ベクトルを $\boldsymbol{x}$ とすれば、$\boldsymbol{\mathsf{v}}'\cdot \boldsymbol{x} = \cos\varphi$、$\boldsymbol{\mathsf{w}}\cdot \boldsymbol{x} = \cos(-\varphi)$ であるが、$\cos\varphi = \cos(-\varphi)$ であるため、$\arccos (\cos\varphi) = \arccos (\cos(-\varphi))$ となってしまい逆関数 $\arccos$ を使っても実際の角度が $\varphi$ であるのか $-\varphi$ であるのかまでは識別できないのである (ある単位ベクトルと x軸との内積が $\cos X$ であったとしても、実際のなす角が $X$ であるのか $-X$ であるのかは逆関数 $\arccos$ からはわからない。上記の $\theta$ の場合は角度の範囲が $0 \leq \theta \leq \pi$ に制限されているからこのような問題を考える必要はない)。
図F5 ベクトルのなす角を求める際、逆関数 $\arccos$ を使うとこのような点に注意しなければいけないわけである ($\sin$ や $\tan$ の逆関数 $\arcsin$ や $\arctan$ でも同様の問題がある)。しかし平面上のベクトルのなす角を求めるにはよく知られた方法がある。それは $\arctan 2$ という関数を使うのである。
この関数は具体的にはXY平面上において x軸からの回転角度を求める関数であるが、引数には x座標と y座標を指定する。UnityのC# APIに用意されている $\arctan 2$ は Mathf.Atan2(y, x) という関数であるが、この関数の場合は第1引数に y座標、第2引数に x座標を指定する (数学ライブラリによって異なるが、atan2 の第1引数、第2引数が y、x の順序はよく見られる。もちろん x、y の順で指定するライブラリもある)。
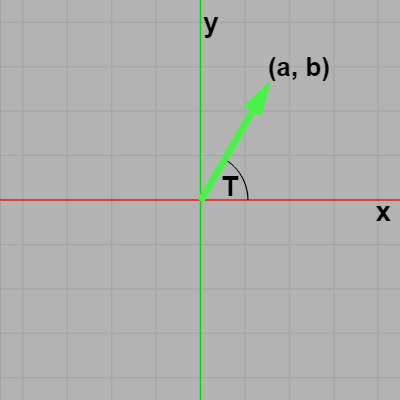
例えば右図のベクトルはXY平面上にあるが、その終点の座標を $(a, b)$、x軸からの回転角度を $T$ とする。このとき $T$ を度数法で求めるには次のように記述すればよい。
$\arctan 2$ による角度の計算はXY平面上であることが前提となっている。下右図に示されるように左手系のXZ平面は y軸プラス側から(x軸プラス方向が右に来るように)見下ろした際、XY平面と同じく x軸プラス方向は右、z軸プラス方向は上である。そのため、$\arctan 2$ 使う際は第1引数に y座標の代わりに z座標をそのまま使えばよいが1つ注意しなければいけない点がある。
図F6 XY平面 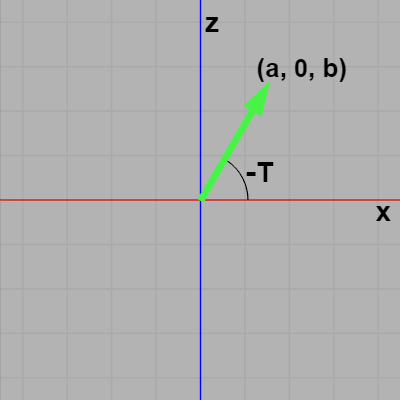
図F7 XZ平面 (左手系において y軸プラス側から見下ろしたときの図)
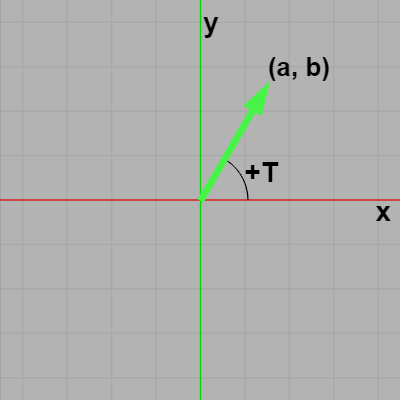
図F6はXY平面上の先程のベクトルでありその終点は $(a, b)$、図F7はXZ平面上のベクトルでありその終点は $(a, 0, b)$ である。XZ平面上におけるこのベクトルの x軸からの回転角度を求める際に注意しなければいけないことは回転の方向である。XY平面の場合、1章や2章で見たように角度を増加させる回転は反時計周りである。しかし左手系において y軸プラス側からXZ平面を見下ろしたときの、角度を増加させる(y軸周りの)回転は時計周りなのである (前節あるいは3-10節参照)。
つまり図F6のベクトルはXY平面において x軸から角度 $+T$ だけ回転した位置にあるが、図F7のベクトルはXZ平面において x軸から角度 $-T$ だけ回転した位置にあるということである。したがって、XZ平面上におけるベクトルの x軸からの回転角度を $\arctan 2$ を用いて求める場合には符号を変える必要があり、例えば図F7のベクトルの場合では x軸からの回転角度は -Mathf.Atan2(b, a) としてマイナスを付けなければならない。
上図F4の y軸周りの回転角度 $\varphi$ は x軸から $\boldsymbol{\mathsf{v}}'$ への回転角度であるから、$\arctan 2$ を用いて簡単に求めることができる。$\boldsymbol{\mathsf{v}}'$ は $\boldsymbol{\mathsf{v}} = (\mathsf{v_x},\ \mathsf{v_y},\ \mathsf{v_z})$ をXZ平面上に射影したベクトルであるから、$\boldsymbol{\mathsf{v}}' = (\mathsf{v_x},\ 0,\ \mathsf{v_z})$ であり、したがって $\varphi$ を度数法で求めるには以下のように計算すればよい。
まとめると初期状態で y軸プラス方向を向いている単位ベクトル $\boldsymbol{\mathsf{v}}$ を下図F1に示される向きに向けるには、$0 \leq \theta \leq \pi$、$-\pi \leq \varphi \leq \pi$ とするとき、$\boldsymbol{\mathsf{v}}$ に対して z軸周り $-\theta$、y軸周りに $\varphi$ の順で回転を行えばよい。プログラムにすると次のようになる。
4行目の Rz は z軸周りの $-\theta$ の回転、9行目の Ry は y軸周りの $\varphi$ の回転を表す回転行列である (回転行列については 3-10節で解説する)。
繰り返しになるが上記の角度制限の下では z軸周りの回転角度は $\theta$ ではなく $-\theta$ であること、また $\varphi$ を求める際にも $\arctan 2$ にマイナスをつけることに注意しよう。

図F1 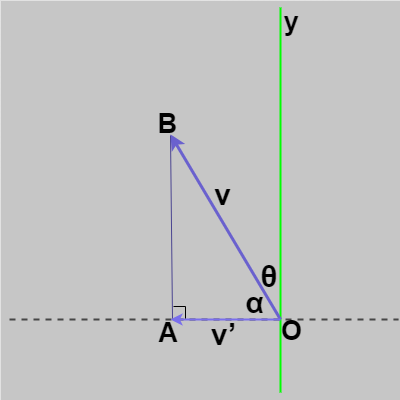
図F8 $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}'$ のなす角 $\alpha$ (点線はXZ平面)
なおここで算出される角度 $\theta$ は $\boldsymbol{\mathsf{v}}$ と y軸とのなす角であったから、$\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}'$ のなす角を $\alpha$ とすれば $\alpha = 90^\circ - \theta$ であるが(上図F8)、$\theta$ を求めずに直接 $\alpha$ を求めることも簡単にできる。図F8に示されるように $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}'$ の作る三角形 $OAB$ を考えれば、これは直角三角形であり、$|OB| = |\boldsymbol{\mathsf{v}}| = 1$、$|AB| = \mathsf{v_y}$ より、$\sin \alpha = \mathsf{v_y}$ である。したがって、$\alpha = \arcsin (\mathsf{v_y})$ とすればよい ($\sin$ の逆関数 $\arcsin$ が返す値の範囲は $-\pi/2$ ~ $\pi/2$)。
(注意 : $\arctan 2$ と似た関数に $\arctan$ という関数がある。いずれも $\tan$ の逆関数であるが、この2つの関数には重要な違いがある。 2つの関数はどちらもXY平面上において x軸からの角度を求めるものであり、その引数は $\arctan 2$ の場合は上で述べたように x座標、y座標を、$\arctan$ の場合は傾きをセットする。例えば下左図のベクトルの場合、その終点は $(a,\ a)$ であるから傾きは $1$ であり、x軸からの回転角度を求めるにはそれぞれ、$\arctan 2 (a,\ a)$、$\arctan (1)$ とすることになる。
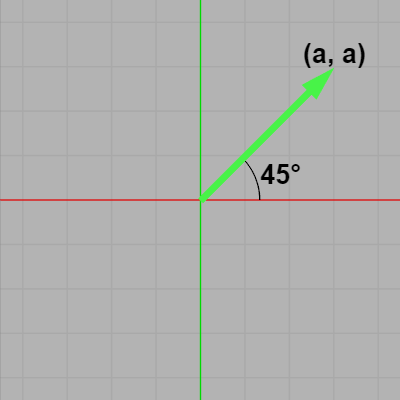
図F9 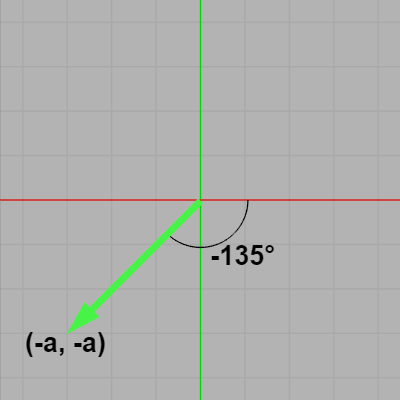
図F10
この場合2つの関数から返される値は同じで $\pi/4\ (= 45^\circ)$ であり、確かに回転角度として正しい値が返される。しかし右図の場合はそうはいかない。右図のベクトルはその終点が $(-a,\ -a)$ であり、x軸からの回転角度は $-3\pi/4\ (= -135^\circ)$ である。$\arctan 2 (-a, -a)$ ではこの角度が返されるが、$\arctan$ の場合は傾きが左図のものと同じ $1\ (=-a/-a)$ なので $\arctan (1)$ となり、その結果 $-3\pi/4$ ではなく左図の場合と同じ $\pi/4$ が返されることになる。つまり $\arctan 2$ は $360^\circ$ に対応するが、$\arctan$ は $360^\circ$ には対応していないのである (具体的には $\arctan 2$ が返す範囲は $-\pi$ ~ $\pi$ であるが、$\arctan$ が返す範囲は $-\pi/2$ ~ $\pi/2$)。このような理由により、平面上において x軸からの角度を求める場合には $\arctan$ よりも $\arctan 2$ が使われるわけである)

図11 点Pと直線m 
図12 点Pから直線mへの垂線と交点Q
(以下では原点を$O$で表す。)
原点$O$を始点、点$P$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とする。また、直線$m$の方向(原点$O$から点$Q$へ向かう方向)を表す単位ベクトルを$\boldsymbol{u}$とし、その始点を原点に置く。ベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$のなす角を $A$とする(以上は図13参照)。
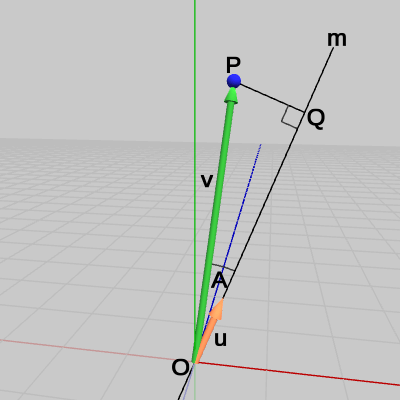
図13 ベクトルvと単位ベクトルu 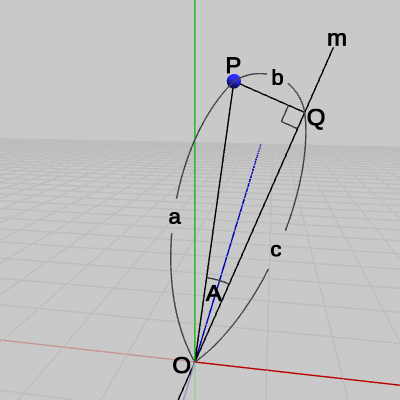
図14 三角形OPQの各辺の長さa、b、c (c = |v|cosA)
ここでベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$の内積を計算すると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}||\boldsymbol{u}|\cos{A} = |\boldsymbol{\mathsf{v}}|\cos{A}\] であるが、この $|\boldsymbol{\mathsf{v}}|\cos{A}$ が何を表すかについて図14を用いて説明しよう。
図14では原点$O$と点$P$、$Q$を結んだ三角形(直角三角形)の各辺に記号がふられてある。これは各辺の長さを表し、すなわち辺$OP$の長さが$a$、辺$PQ$の長さが$b$、辺$OQ$の長さが$c$である。ベクトル$\boldsymbol{\mathsf{v}}$は、$O$と$P$を結ぶベクトルであるから、$\boldsymbol{\mathsf{v}}$の大きさ $|\boldsymbol{\mathsf{v}}|$ は辺$OP$の長さに等しい、すなわち $|\boldsymbol{\mathsf{v}}| = a$ である。
そして、$\triangle{OPQ}$は直角三角形であるから辺$OP$と辺$OQ$の長さについて次の関係が成り立つ。
\[ a\cos{A} = c \] 以上から、
\[ |\boldsymbol{\mathsf{v}}|\cos{A} = c \] つまり $|\boldsymbol{\mathsf{v}}|\cos{A}$ は辺$OQ$の長さに等しいことがわかる。原点$O$から点$Q$の方向を表す単位ベクトルは$\boldsymbol{u}$で、原点$O$から点$Q$までの長さが $|\boldsymbol{\mathsf{v}}|\cos{A}$ であるから、点$Q$の位置は
\[ Q = (|\boldsymbol{\mathsf{v}}|\cos{A})\boldsymbol{u} \] で求められる。
D)において垂線の足である点$Q$を求める過程を再度見直してみよう。
原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$と、直線$m$の方向を表す単位ベクトル$\boldsymbol{u}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}|\cos{A}$ は、原点$O$から点$Q$までの長さに等しいのであった。そして、原点から直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れた位置に、点$P$からの垂線の足である点$Q$はあるのであった。このことを便宜上、「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」という言い方で表す(つまり点$P$の直線$m$方向の距離とは、原点から(垂線の足)点$Q$までの距離である)。
以上をふまえて本題に入る。
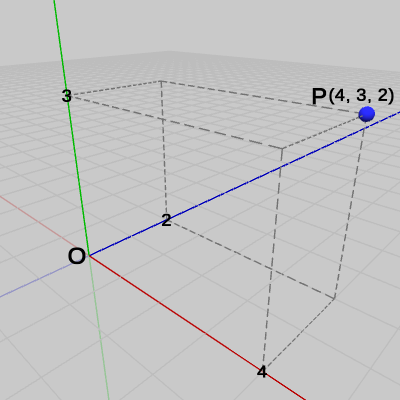
図15 点P = (4, 3, 2) 図15では点$P$が$(4, 3, 2)$の位置に置かれている。今まで特に顧みることはなかったが、点を表す座標値というものは何を意味しているのであろうか。点$P = (4, 3, 2)$とは点$P$のx座標が$4$であり、y座標が$3$、z座標が$2$であることを意味するが、「x座標が$4$」とは具体的には何のことであろうか。いささか自明に過ぎる問いであるが、ここで点の座標について幾らか丁寧な解説を試みよう。
点$P$の座標が$(4, 3, 2)$であるとは、点$P$を図16のように原点に置いてから、まず始めにx軸方向に$4$移動させ(図17)、次にy軸方向に$3$移動させ(図18)、そして最後にz軸方向に$2$移動させる(図15)、この原点からの3回の移動後の$P$の位置のことを意味している。
言い換えれば、点の座標値における各座標(x座標、y座標、z座標)は、その点が原点から各軸の方向にどれだけ離れているかを表している。点$P = (4, 3, 2)$の場合でいえば、点$P$が原点からx軸方向に$4$、y軸方向に$3$、z軸方向に$2$だけ離れていることを表している。
点$P$が原点からx軸方向、y軸方向、z軸方向にどれだけ離れているかは図15を見ればわかるが、ここでは内積を使ってその距離を計算してみよう。
そのために原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と、x軸、y軸、z軸の各方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$、$\boldsymbol{u_y} = (0, 1, 0)$、$\boldsymbol{u_z} = (0, 0, 1)$を用意する(図19、図20)。
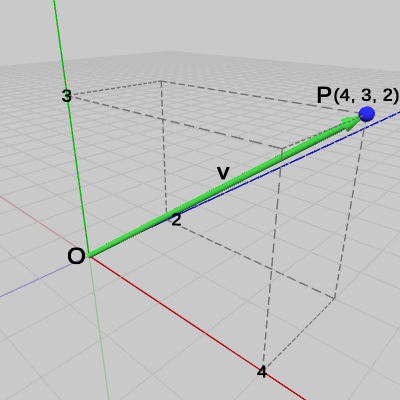
図19 ベクトルv 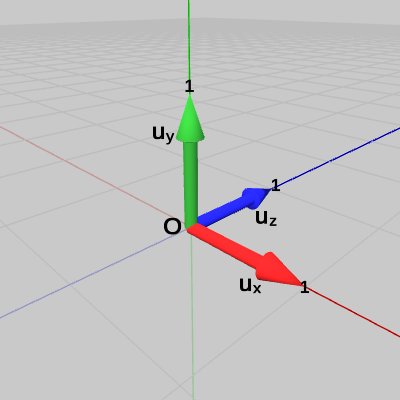
図20 単位ベクトルux、uy、uz
まず、点$P$が原点からx軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とx軸方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_x}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} = 4\cdot1 + 3\cdot0 + 2\cdot0 = 4\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \] 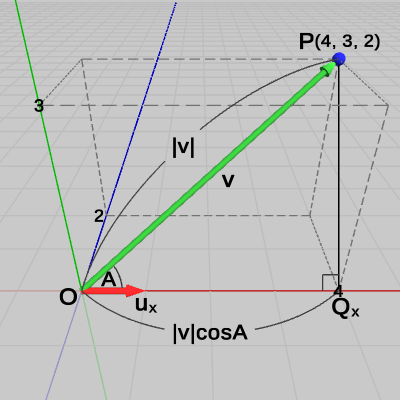
図21 点Pのx軸方向の距離 であるが、この内積が何を表すかは D)で述べたが、再度図21を使って説明しよう。
点$P$からx軸へ垂線をおろし、その足を点$Q_x$とする($\triangle{OPQ_x}$は直角三角形になる)。D)で見たように、原点$O$から点$Q_x$までの距離は、原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$とx軸方向の単位ベクトル$\boldsymbol{u_x}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} (= |\boldsymbol{\mathsf{v}}|\cos{A})$ であるが、これは上で求めたとおり $4$ である。
先程、D)の点$P$について次のような言い方を用いた。「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」。この表現を今の例にあてはめると、直線$m$はx軸に相当し、ここでの$|\boldsymbol{\mathsf{v}}|\cos{A}$は$4$であるので、「点$P$はx軸の方向に$4$だけ離れている」という内容になる。
点$P$が原点からx軸方向にどれだけ離れているかを内積を使って求めるというのが、ここでの目的であったが、今述べてきたことがそれにあたるわけである。
点$P$のy軸方向の距離、z軸方向の距離についても同様の手順で求めることができる。
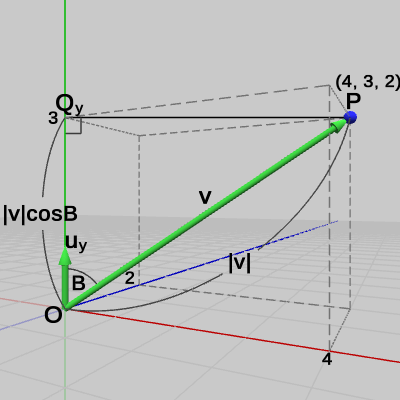
図22 点Pのy軸方向の距離 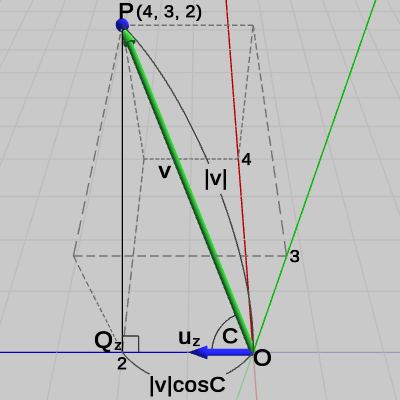
図23 点Pのz軸方向の距離
図22に示されるようにy軸方向の距離は、点$P$からy軸におろした垂線の足を点$Q_y$とすれば、原点から$Q_y$までの距離のことである($\triangle{OPQ_y}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とy軸方向を表す単位ベクトル$\boldsymbol{u_y} = (0, 1, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_y}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_y} = 4\cdot0 + 3\cdot1 + 2\cdot0 = 3\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \] x軸の場合と同様に、この結果は「点$P$はy軸の方向に$3$だけ離れている」ことを意味している。
図23に示されるようにz軸方向の距離は、点$P$からz軸におろした垂線の足を点$Q_z$とすれば、原点から$Q_z$までの距離のことである($\triangle{OPQ_z}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とz軸方向を表す単位ベクトル$\boldsymbol{u_z} = (0, 0, 1)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_z}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_z} = 4\cdot0 + 3\cdot0 + 2\cdot1 = 2\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \] この結果は「点$P$はz軸の方向に$2$だけ離れている」ことを意味している。
だが、以上に述べてきた事柄はおそらく自明過ぎるものであろう。x軸、y軸、z軸のような基本的な座標軸上での点の位置は、そもそも点の座標値から分かることであって、わざわざ内積を使ってまで求める必要はない。確かに今まで用いてきた座標系(と座標値)ならばそれはいえる。しかし、例えばこの同じ点$P$を図24に示されるような水色、紫色、黄色の座標軸を持つ傾いた座標系を基準にした場合などでは、いささか状況が異なってくる。
図24 ijk座標系 
図25 ijk座標系(離れた位置から)
図24に示される座標系は互いに直交する i軸(水色)、j軸(紫色)、k軸(黄色)によって構成される座標系で、便宜上ここでは ijk座標系と呼ぶことにする(図25はやや離れた位置から ijk座標系を見たもの。また、i軸、j軸、k軸についてはプラス側のみ表示してある)。そして、今まで用いてきた x軸、y軸、z軸の座標系の方をxyz座標系と呼ぶことにする。
図からわかる通り ijk座標系は傾いた座標系であり、xyz座標系とは原点が一致している。
今から問題とするのは、上で使ってきた点$P$の ijk座標系における座標値の計算である。すなわち、点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離を求めることであり、それは図26における点線の直方体の3つの辺の長さ$a$、$b$、$c$を求めることと同じである(図27は見やすくするためにxyz座標系を取り除いたもの。図における点線の図形は直方体であるので隣接する面の間の角度は直角である)。

図26 ijk座標系における点P = (a, b, c) 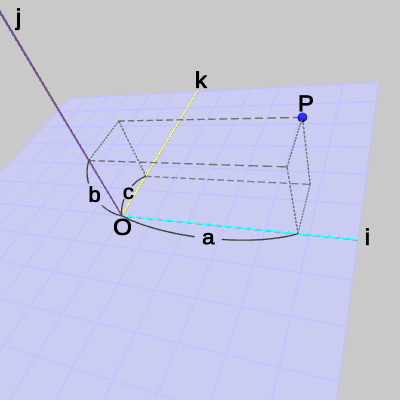
図27 ijk座標系における点P = (a, b, c)
xyz座標系における$P$の座標は$(4, 3, 2)$であったが、ijk座標系での座標は図27を見ると、そのような整数値でないことは明らかである(もちろん点$P$の位置は今までの位置から動かしていない)。
しかし、点$P$の ijk座標系における座標を計算するのは難しいことではない。今まで見てきたことをなぞっていけば、自ずと答えが導かれる。ただし、注意すべきことが1つある。今、座標系が2つ出てきたが、この先で使用する、原点と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$、i軸、j軸、k軸の方向を表す単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$などは全てxyz座標系での値である。例えば、何度も出てきたが$(4, 3, 2)$という点$P$の座標はxyz座標系での値である。ijk座標系では図26(あるいは図27)に示されるように点$P$は$(a, b, c)$であり、$(4, 3, 2)$ではない (これは 点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離が $a$、$b$、$c$ であり $4$、$3$、$2$ ではないことを意味する)。
計算手順については今までと同様である。
まず、原点$O$から点$P$へのベクトル$\boldsymbol{\mathsf{v}}$を用意する(図28)。xyz座標系での値であるので、今までどおり、$\boldsymbol{\mathsf{v}} = (4, 3, 2)$である。また、i軸方向、j軸方向、k軸方向の単位ベクトルを$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$とする(図29。図からわかるようにこれらもxyz座標系での値であり、小数3位以下を省略してある)。
図の緑色の数値はベクトルの内容を表している。

図28 ベクトルv = (4, 3, 2) 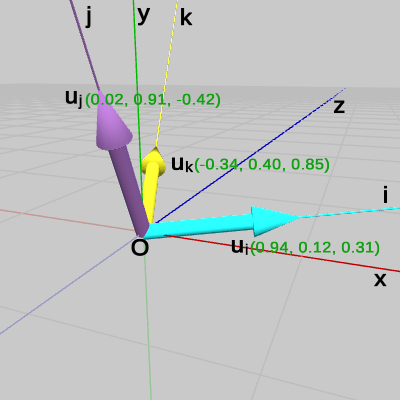
図29 単位ベクトルui、uj、uk
(以下で使用される単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$は小数第3位以下を省略した値であるため、それらを使った計算結果もわずかな誤差を含んでいる。)
では、点$P$が原点から i軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と i軸方向を表す単位ベクトル$\boldsymbol{u_i} = (0.94, 0.12, 0.31)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_i}$のなす角を$A$とすると、
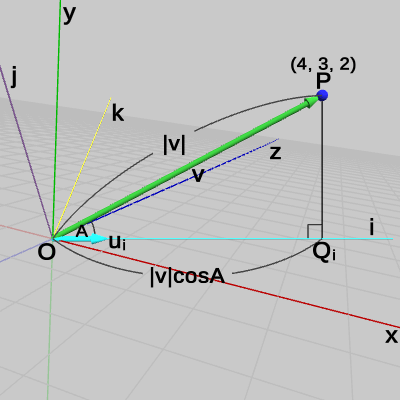
図30 点Pの i軸方向の距離 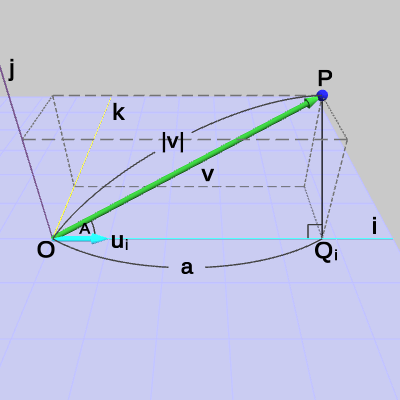
図31 点Pの i軸方向の距離(ijk座標系のみで表示)
点$P$が原点から j軸方向にどれだけ離れているかについても同様に計算してみよう。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と j軸方向を表す単位ベクトル$\boldsymbol{u_j} = (0.02, 0.91, -0.42)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_j}$のなす角を$B$とすると、
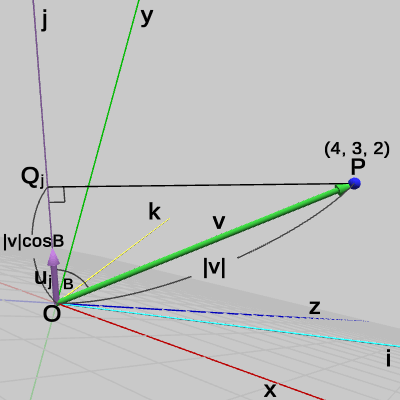
図32 点Pの j軸方向の距離 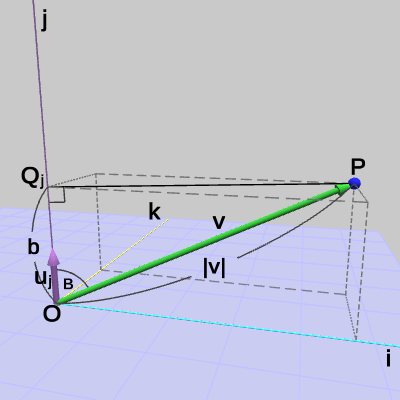
図33 点Pの j軸方向の距離(ijk座標系のみで表示)
点$P$のk軸方向の距離についても同様の手順を繰り返せばよい。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とk軸方向を表す単位ベクトル$\boldsymbol{u_k} = (-0.34, 0.40, 0.85)$の内積は、
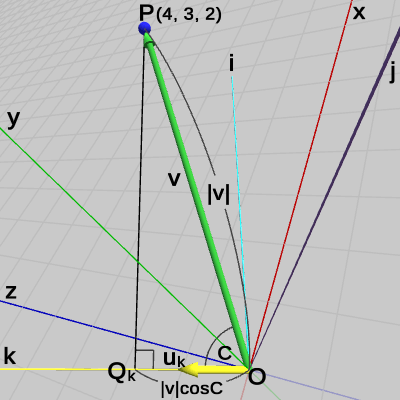
図34 点Pのk軸方向の距離 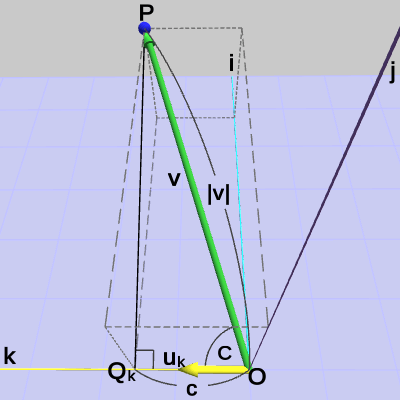
図35 点Pのk軸方向の距離(ijk座標系のみで表示)
以上の結果をまとめると、点$P$の ijk座標系における座標(i座標、j座標、k座標)は、
\[P = (4.74,\ 1.97,\ 1.54)\]であることがわかった(図36)。
比較のために図37にxyz座標系での点$P$を示す。
また、今までの計算で使われてきた単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$の値はxyz座標系での値であったが参考のために ijk座標系での値を以下に示しておこう(図38参照。以下のカッコの中の数値は i座標、j座標、k座標の順である)。
\begin{align*}\boldsymbol{u_i} = (1, 0, 0) \\\boldsymbol{u_j} = (0, 1, 0) \\\boldsymbol{u_k} = (0, 0, 1) \\\end{align*}
最後に、本節で述べた内容に関してのプログラムを作成する。
Unityで内積を求める場合には次のメソッドが用意されている。
[Code1] (実行結果 図39)
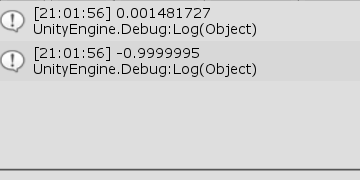
図39 3行目の Dot(..)には引数として v1.normalized、v2.normalized が指定されているが、これによりベクトルv1、v2の単位ベクトルの内積が算出される。図39の実行結果では、最初の計算の内積が 0.0014... となっており、非常に $0$に近い値である。本節 B) の「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が $0$であるときは、その2つのベクトルは直交している。つまり、最初の計算における v1、v2のなす角は非常に$90$°に近いということがわかる。
第2の計算は v1、v2の値を変えて、再び単位ベクトルの内積を計算したものである。
実行結果は -0.9999... となっており、今度は非常に$-1$近いに値である。「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が$-1$であるときは、その2つのベクトルは平行であるが、向きは反対である。したがって、第2の計算における v1、v2のなす角は非常に$180$°に近いということがわかる。
各点の座標は $A = (2.77,\ 5.0,\ 2.36)$、$B = (3.05,\ 4.41,\ 4.25)$、$C = (2, 5, 3)$ である。
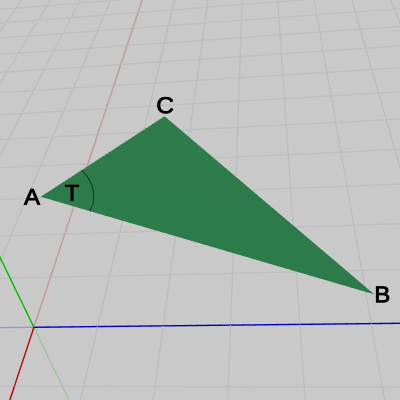
図40 △ABC と ∠T 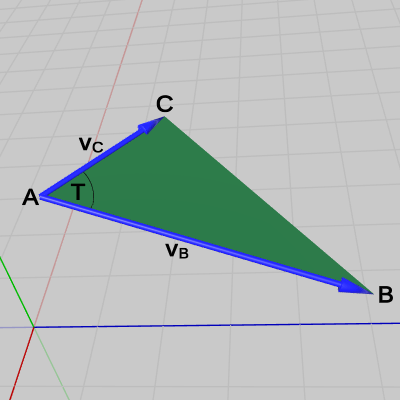
図41 ベクトルvBとvC
まず先にプログラムを示す。
[Code2] (実行結果 図42)
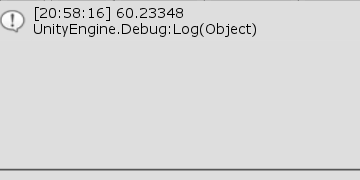
図42 Code2 実行結果 1行目から3行目の A、B、C は図における $A$、$B$、$C$ の各位置を表している。4行目、5行目の vB は $A$ を始点とし$B$を終点とするベクトル、vC は $A$ を始点とし $C$ を終点とするベクトルである (図41)。6行目において その2つのベクトルの単位ベクトルの内積を算出しているが、辺 $AB$ と辺 $AC$ のなす角は図に示されるように $\angle T$ であるから、この内積の値dotは $\cos T$ に等しい (本節 B) の「ベクトルのなす角」参照)。
7行目の Acos(..) は $\cos$ 関数の逆関数で、$\cos\theta$ から $\theta$ を求める際に使用する。6行目のdotは $\cos T$ に等しいので、7行目の Acos(dot) によって返される値は角度 $T$ である。しかし、ここで注意することがある。Acos(..) から返される角度は弧度法の値($\pi / 2$、$\pi$ などで単位はラジアン)になっているという点である。
8行目では7行目で算出された radian に Mathf.Rad2Deg を掛けているが、これによって弧度法の値から度数法の値($30^\circ$、$60^\circ$ など)に変換されるのである (Mathf.Rad2Degは、弧度法の値から度数法の値に変換するときに、弧度法の値に掛ける定数)。
実行結果(図42)では 60.23... と出力されているが、これは $\angle T$ が約 $60^\circ$ であることを示している。
例えばベクトルの大きさを比較する際、2つのベクトル $\boldsymbol{\mathsf{v}_1} = (x_1,\ y_1,\ z_1)$、$\boldsymbol{\mathsf{v}_2} = (x_2,\ y_2,\ z_2)$ の大きさは\[ |\boldsymbol{\mathsf{v}_1}| = \sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2} \qquad ,\qquad |\boldsymbol{\mathsf{v}_2}| = \sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2}\]として求められるが(3-1節)、2つのベクトルの大きさの比較においては平方根を使っても使わなくても大小関係は同じである。$|\boldsymbol{\mathsf{v}_1}|$、$|\boldsymbol{\mathsf{v}_2}|$ の例でいえば $|\boldsymbol{\mathsf{v}_1}| < |\boldsymbol{\mathsf{v}_2}|$ であることは\[ \sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2} < \sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2} \tag{1}\]を意味するが、この場合は平方根を取った以下の式も成り立つ。\[ {x_1}^2 + {y_1}^2 + {z_1}^2 < {x_2}^2 + {y_2}^2 + {z_2}^2 \tag{2}\]つまり (1) が成り立つならば (2) が成り立ち、逆に (2) が成り立つ場合でも (1) は成り立つから、結局2つのベクトルの大きさを比較する際には平方根を使う必要はないのである。
実際のコードでは次のように書くよりも次の形で書く方が効率的なのである。
sqrMagnitude はVector3型に用意されているプロパティで大きさの2乗を返すものである。$\boldsymbol{\mathsf{v}} = (x, y, z)$ であれば v.sqrMagnitude は $x^2 + y^2 + z^2$ を意味する。
あるいはコンピューターグラフィックスのプログラムではこの2乗の比較は次のように書かれることもある。
この Dot(v, v) という計算は v.sqrMagnitude を別の形で表現しているに過ぎない。
今回作成するプログラムもこの「平方根を使わない」ことに関連するものであるが、このプログラムは読者用の課題である。
ともに始点が $A$ の2つのベクトル $\overrightarrow{AB}$、$\overrightarrow{AC}$ が適当な位置に置かれている (図43)。この2つのベクトルの大きさはそれぞれ異なり、2つともその大きさは $1$ ではない。
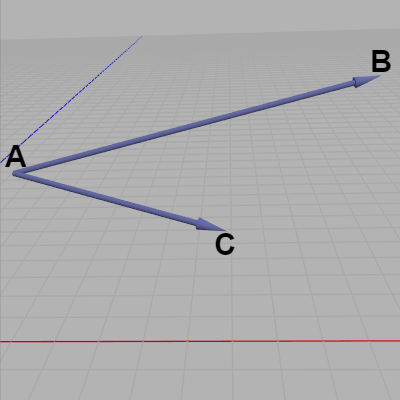
図43 2つのベクトル $\overrightarrow{AB}$、$\overrightarrow{AC}$ (ともにその大きさは $1$ ではない) 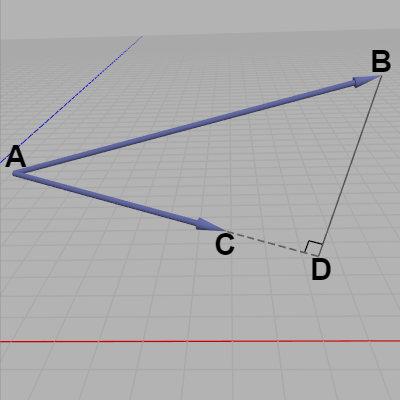
図44
ここでベクトル $\overrightarrow{AC}$ に直交するベクトルを求めるとする。その場合図44のように $\overrightarrow{AC}$ の延長上に点 $D$ を、三角形 $ABD$ が直角三角形になるように置けば、ベクトル $\overrightarrow{DB}$ が求めるベクトルである。
ここでの課題は $\overrightarrow{AC}$ と直交する上記のベクトル $\overrightarrow{DB}$ を求めることであるが、このベクトルを求める際には平方根を使わずに求めるものとする。平方根を使わないということは magnitude や normalized のようなプロパティ、あるいは Normalize() のようなメソッドも使うことはできない (ただし上記の sqrMagnitude を使うことは問題ない)。
このプログラムには次の定数が用意されている。
プログラムはCode3に作成するものとする。
[Code3] (実行結果 図45)
図45 Code3 実行結果 (正しい計算が行われれば (2, 3, 4) という値が出力される) 最初の段階ではCode3には $(0, 0, 0)$ がセットされたベクトル vDB を出力する処理が記述されているが、この vDB の内容を適当に書き換えて上記の $\overrightarrow{AC}$ と直交するベクトルになるようにすることがここでの課題である。
特に直接的な影響はないので答えから先にいえば、正しく計算が行われた場合出力される vDB の値は $(2, 3, 4)$ という値になる。
(解答例のプログラムは Sec304_Ans.txt を参照 ; Sec304_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
下左図の2つのベクトル $V_1$、$V_2$ は同じ大きさのベクトルであり、$V_1$ は x軸プラス方向を向いている。この状態から $V_1$ を適当に回転させて $V_2$ に重ねる回転を考えよう。
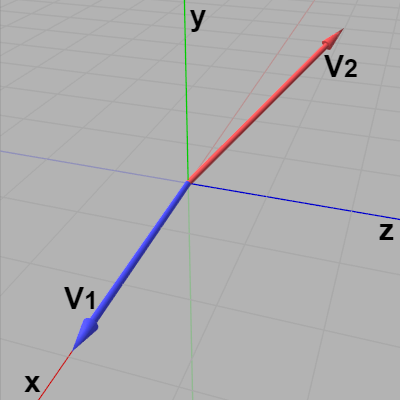
図46 $V_1$、$V_2$ は同じ大きさのベクトル ($V_1$ の向きは x軸プラス方向) 
図47 $V_1$ を回転させて $V_2$ に重ねた状態
そのためには下図のように、まず $V_1$ を z軸周りに回転させ、続いて y軸周りに回転させれば目的の状態にすることができる。この回転における z軸周りの回転角度を $\alpha$、y軸周りの回転角度を $\beta$ とする。

図48 z軸周り、y軸周りの順で回転させる
ここでの課題はこの2つの回転角度 $\alpha$ 及び $\beta$ を求めることである ($\alpha$、$\beta$ は弧度法ではなく度数法の角度)。
上記の解説では同様の問題を扱ったが、そこではベクトルの初期状態の向きは y軸プラス方向であった。この課題の場合は初期状態が x軸プラス方向であるが、考え方は同じである。上で述べた手続きをそのまま適用すればよい。
プログラムには以下の定数が用意されている。
プログラムはCode4に作成するものとし、$V_1$ の回転は S キーが押された際に行われるものとする。
[Code4] (実行結果 図47)
4行目の alpha に z軸周りの回転角度 $\alpha$ を、5行目の beta に y軸周りの回転角度 $\beta$ をセットするだけでよい。最初の段階ではいずれも $0$ がセットされているが、この場合には S キーを押しても何も変化しない。alpha、beta に適切な値がセットされていれば S キーが押されると図46の状態から図47の状態になる (最初の状態に戻すには C キーを押せばよい)。
回転角度を求める際にはその符号に注意しなければならない。前節で見たように(左手系の場合には)左手の親指を回転軸に向けたときの残りの指の曲がっている方向が回転のプラス方向、つまり回転角度の符号をプラスにする回転である。
上の解説でも述べたことであるが弧度法から度数法の変換について再度触れておこう。
角度を求める逆関数 Asin、Acos、Atan2 は弧度法の角度($\pi/4$、$\pi/2$ など)で返されるので、それを度数法の角度($45^\circ$、$90^\circ$ など)に変換するためにはUnityに用意されている定数 Mathf.Rad2Deg を以下のように使用する。
(解答例のプログラムは Sec304_Ans.txt を参照)
A) ベクトルの内積
3D空間においては、ベクトルの内積は次のように定義される。ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$の内積 $\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2\]
(計算例)
ベクトル$\boldsymbol{\mathsf{v_1}} = (1, 2, 3)$と $\boldsymbol{\mathsf{v_2}} = (6, 5, 4)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 1\cdot6 + 2\cdot5 + 3\cdot4 = 6 + 10 + 12 = 28\] ベクトル$\boldsymbol{\mathsf{v_1}} = (3, -1, -5)$と $\boldsymbol{\mathsf{v_2}} = (0,\ 5, -1)$の内積
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = 3\cdot0 + (-1)\cdot5 + (-5)\cdot(-1) = 0 + (-5) + 5 = 0\]
定義から明らかなように、内積は以下のように積の順序について交換可能である。
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = \boldsymbol{\mathsf{v_2}}\cdot\boldsymbol{\mathsf{v_1}}\]
また、同じベクトル同士の内積、例えばベクトル$\boldsymbol{\mathsf{v}} = (x, y, z)$同士の内積は、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = xx + yy + zz = x^2 + y^2 + z^2\] となるが、これはベクトル$\boldsymbol{\mathsf{v}}$の大きさ($|\boldsymbol{\mathsf{v}}| = \sqrt{x^2 + y^2 + z^2}$)の$2$乗に等しい。すなわち、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{\mathsf{v}} = |\boldsymbol{\mathsf{v}}|^2\] である。
B) ベクトルのなす角
ベクトルの内積は、ベクトルのなす角と密接な関係がある。すなわち、次の等式が成り立つ。ベクトル$\boldsymbol{\mathsf{v_1}} = (x_1, y_1, z_1)$と $\boldsymbol{\mathsf{v_2}} = (x_2, y_2, z_2)$のなす角を $A$とし、$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の大きさを$|\boldsymbol{\mathsf{v_1}}|$、$|\boldsymbol{\mathsf{v_2}}|$とすれば
\[ \boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}} = x_1x_2 + y_1y_2 + z_1z_2 = |\boldsymbol{\mathsf{v_1}}||\boldsymbol{\mathsf{v_2}}|\cos{A}\] である。
図1のベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$は、両者のなす角が $A$である。図2は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である(両者のなす角は変わらない)。


上の等式における$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$の代わりに単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$を式に使った場合、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = |\boldsymbol{u_1}||\boldsymbol{u_2}|\cos{A} \] となるが、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$は単位ベクトルであるから、$|\boldsymbol{u_1}|$、$|\boldsymbol{u_2}|$の値は$1$である。すなわち、\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} \] が成り立つ。
この結果は、2つのベクトルの単位ベクトルの内積を求めれば、その2つのベクトルのなす角を知ることが可能であることを意味している。
以下では、その特殊な例として2つのベクトルが直交している場合、あるいは平行である場合の判定方法について見ていく。
(注) 以下の例ではベクトルのなす角は、0°~180°の範囲にあるものとする。
(例1) 2つのベクトルが直交しているかどうかの判定(なす角が$90$°)


図3に示されるベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$のなす角を $A$とする。図4は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0\] 上で述べたように、単位ベクトルの内積はそれらのなす角の余弦($\cos$)に等しいから、結局\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 0\] となる。
$\cos{A} = 0$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 90$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$0$になる場合では、両者は直交していることがわかる(2つのベクトルが直交している場合は、両者を正規化せずに内積を計算しても結果は$0$になる。つまり、この例では$\boldsymbol{\mathsf{v_1}}\cdot\boldsymbol{\mathsf{v_2}}$の値も$0$である)。
(例2) 2つのベクトルが平行であるかどうかの判定 1 (なす角が$0$°)
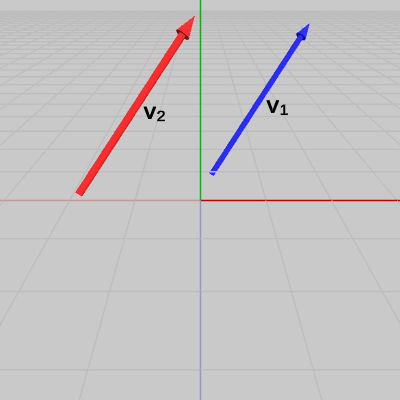 図5 ベクトルv1、v2
図5 ベクトルv1、v2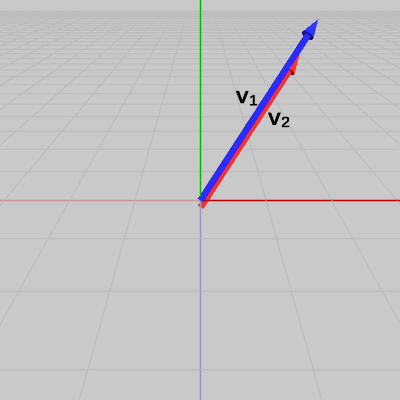 図6 ベクトルv1、v2の始点を原点に移動させる
図6 ベクトルv1、v2の始点を原点に移動させる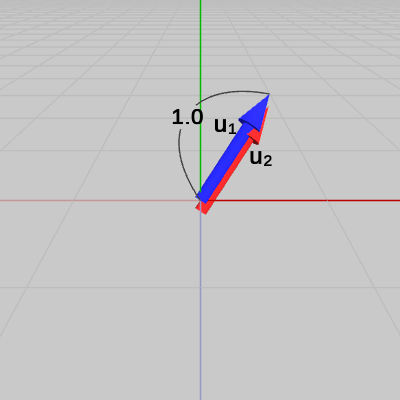 図7 ベクトルv1、v2を正規化したu1、u2
図7 ベクトルv1、v2を正規化したu1、u2
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図5に示される位置に置かれている。この2つのベクトルのなす角は、両者の始点を原点に移動させたときの2つのベクトルのなす角のことである。今回の例では、2つのベクトルを原点に移動させたときに(図6)、2つのベクトルが重なってしまっているので角度の表示がされていないが、ここでも両者のなす角を$A$とする。
図7は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1\] 先程と同じように、両者のなす角の余弦($\cos$)を使って表せば、
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = 1\] となる。
$\cos{A} = 1$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 0$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$1$になる場合では、両者は平行でありベクトルの向きも同じであることがわかる。
(例3) 2つのベクトルが平行であるかどうかの判定 2 (なす角が$180$°)
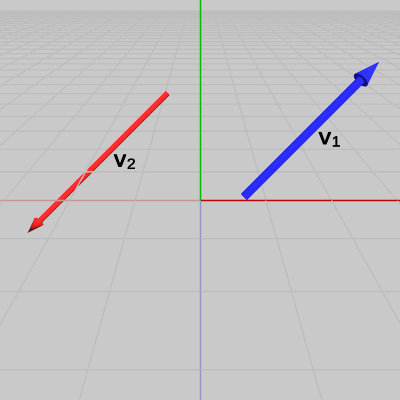 図8 ベクトルv1、v2
図8 ベクトルv1、v2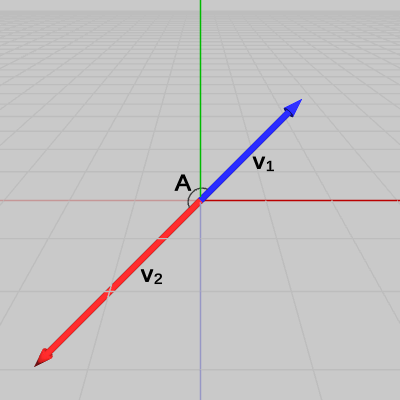 図9 ベクトルv1、v2の始点を原点に移動させる
図9 ベクトルv1、v2の始点を原点に移動させる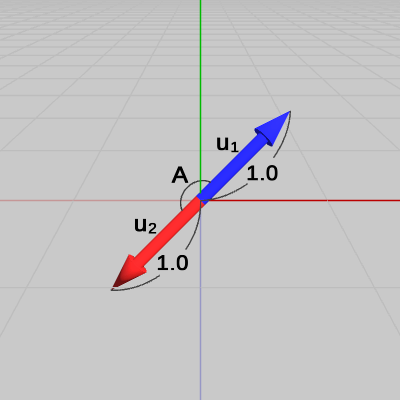 図10 ベクトルv1、v2を正規化したu1、u2
図10 ベクトルv1、v2を正規化したu1、u2
2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$が図8に示される位置に置かれている。この2つのベクトルのなす角は、上の例で述べたように両者の始点を原点に移動させたときの2つのベクトルのなす角のことであり、図9に示されるようにここでも両者のなす角を$A$とする。
図10は、この2つのベクトルを正規化したものを$\boldsymbol{u_1}$、$\boldsymbol{u_2}$として示した図である。
このとき、$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積が次のような結果であったとしよう。
\[ \boldsymbol{u_1}\cdot\boldsymbol{u_2} = \cos{A} = -1\] $\cos{A} = -1$ を満たす角度$A$は($0$°~$180$°の範囲では)、$A = 180$°の場合のみである。
したがって、この例のように2つのベクトルの単位ベクトルの内積が$-1$になる場合では、両者は平行であるがベクトルの向きは逆向きであることがわかる。
以上をまとめると、2つのベクトル$\boldsymbol{\mathsf{v_1}}$、$\boldsymbol{\mathsf{v_2}}$ 及び、それらの単位ベクトル$\boldsymbol{u_1}$、$\boldsymbol{u_2}$の内積について次のことがいえる。
(ⅰ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 0$ のとき、2つのベクトルは直交する。
(ⅱ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = 1$ のとき、2つのベクトルは平行であり同じ向きである。
(ⅲ) $\boldsymbol{u_1}\cdot\boldsymbol{u_2} = -1$ のとき、2つのベクトルは平行であり逆向きである。
ここではベクトルのなす角の範囲を$0$°~$180$°の範囲に制限したが、この範囲を$0$°より下、あるいは$180$°より上の範囲に広げても上記の(ⅰ)~(ⅲ)は成立する。
C) ベクトルの角度の計算
ベクトルのなす角に関連して、簡単な例を用いてベクトルの角度の求め方について解説する。ベクトル $\boldsymbol{\mathsf{v}}$ を単位ベクトルとし、$\boldsymbol{\mathsf{v}}$ をXZ平面上へ射影したベクトルを $\boldsymbol{\mathsf{v}}'$ とする (下図F1)。また y軸とのなす角を $\theta$、$\boldsymbol{\mathsf{v}}'$ と x軸とのなす角を $\varphi$ とし、それぞれの角度の範囲を $0 \leq \theta \leq \pi$、$-\pi \leq \varphi \leq \pi$ とする ($\theta$、$\varphi$ がこの範囲であれば、$\boldsymbol{\mathsf{v}}$ を3D空間内の任意の方向に向けることができる)。
単位ベクトル $\boldsymbol{\mathsf{v}}$ が初期状態において y軸プラス方向をむいていたとして、$\boldsymbol{\mathsf{v}}$ を y軸プラス方向から左図の状態にするための角度 $\theta$、$\varphi$ を求めることについて考えよう。


$\theta$ の求め方は簡単である。$\theta$ は $\boldsymbol{\mathsf{v}}$ と y軸のなす角であるから、$\boldsymbol{\mathsf{v}} = (\mathsf{v_x},\ \mathsf{v_y},\ \mathsf{v_z})$、$\boldsymbol{y} = (0, 1, 0)$ とすれば、\[ \boldsymbol{\mathsf{v}}\cdot \boldsymbol{y} = \mathsf{v_y} = \cos\theta \]である。したがって $\cos$ の逆関数 $\arccos$ を使って、$\theta = \arccos(\mathsf{v_y})$ とすればよい ($\arccos$ の引数は $-1$ ~ $1$ の範囲でなければならない。算出される角度の範囲は $0$ ~ $\pi$ である)。
プログラムにすれば以下のように記述される。
// v と y軸のなす角 theta の計算 (v は単位ベクトル) float radTheta = Mathf.Acos(v.y); float degTheta = Mathf.Rad2Deg * radTheta;
ただし回転角度を考える場合には注意が1つ必要である。それはどの軸を回転軸にするかによって回転角度の符号が変わるためである。
例えば上で求めた角度 $\theta$ を z軸周りの回転で使うとしよう。その場合、前節で述べたように z軸プラス方向に(左手の)親指を向けたときの残りの指の曲がっている方向が回転角度の増加方向である。したがって、$\boldsymbol{\mathsf{v}}$ を下図F3のように回転させるには z軸周りに $-\theta$ 回転させる必要があるということである ($0 \leq \theta \leq \pi$ に制限していたから $\theta$ は必ず $0$ 以上の正の値)。


$\boldsymbol{\mathsf{v}}$ を z軸周りに $-\theta$ 回転させた時点では $\boldsymbol{\mathsf{v}}$ はXY平面上にある。$\boldsymbol{\mathsf{v}}$ を目的の方向に向けるには、さらに y軸周りの $\varphi$ の回転を行う必要がある (図F4)。
$\varphi$ は $\boldsymbol{\mathsf{v}}$ をXZ平面上に射影したベクトル $\boldsymbol{\mathsf{v}}'$ と x軸とのなす角であるから、$\boldsymbol{\mathsf{v}}'$ と x軸の内積から上記と同じく $\arccos$ を使って求めることはできる。しかし x軸とのなす角が $\varphi$ ではなく $-\varphi$ であるようなベクトルを $\boldsymbol{\mathsf{w}}$ とすれば、$\boldsymbol{\mathsf{w}}$ と x軸とのなす角は $-\varphi$ であるから、x軸との内積を計算する場合 $\boldsymbol{\mathsf{v}}'$ でも $\boldsymbol{\mathsf{w}}$ でも内積は同じになってしまう。
つまり x軸を表す単位ベクトルを $\boldsymbol{x}$ とすれば、$\boldsymbol{\mathsf{v}}'\cdot \boldsymbol{x} = \cos\varphi$、$\boldsymbol{\mathsf{w}}\cdot \boldsymbol{x} = \cos(-\varphi)$ であるが、$\cos\varphi = \cos(-\varphi)$ であるため、$\arccos (\cos\varphi) = \arccos (\cos(-\varphi))$ となってしまい逆関数 $\arccos$ を使っても実際の角度が $\varphi$ であるのか $-\varphi$ であるのかまでは識別できないのである (ある単位ベクトルと x軸との内積が $\cos X$ であったとしても、実際のなす角が $X$ であるのか $-X$ であるのかは逆関数 $\arccos$ からはわからない。上記の $\theta$ の場合は角度の範囲が $0 \leq \theta \leq \pi$ に制限されているからこのような問題を考える必要はない)。

この関数は具体的にはXY平面上において x軸からの回転角度を求める関数であるが、引数には x座標と y座標を指定する。UnityのC# APIに用意されている $\arctan 2$ は Mathf.Atan2(y, x) という関数であるが、この関数の場合は第1引数に y座標、第2引数に x座標を指定する (数学ライブラリによって異なるが、atan2 の第1引数、第2引数が y、x の順序はよく見られる。もちろん x、y の順で指定するライブラリもある)。
例えば右図のベクトルはXY平面上にあるが、その終点の座標を $(a, b)$、x軸からの回転角度を $T$ とする。このとき $T$ を度数法で求めるには次のように記述すればよい。
float radT = Mathf.Atan2(b, a); float degT = radT * Mathf.Rad2Deg;
$\arctan 2$ による角度の計算はXY平面上であることが前提となっている。下右図に示されるように左手系のXZ平面は y軸プラス側から(x軸プラス方向が右に来るように)見下ろした際、XY平面と同じく x軸プラス方向は右、z軸プラス方向は上である。そのため、$\arctan 2$ 使う際は第1引数に y座標の代わりに z座標をそのまま使えばよいが1つ注意しなければいけない点がある。


図F6はXY平面上の先程のベクトルでありその終点は $(a, b)$、図F7はXZ平面上のベクトルでありその終点は $(a, 0, b)$ である。XZ平面上におけるこのベクトルの x軸からの回転角度を求める際に注意しなければいけないことは回転の方向である。XY平面の場合、1章や2章で見たように角度を増加させる回転は反時計周りである。しかし左手系において y軸プラス側からXZ平面を見下ろしたときの、角度を増加させる(y軸周りの)回転は時計周りなのである (前節あるいは3-10節参照)。
つまり図F6のベクトルはXY平面において x軸から角度 $+T$ だけ回転した位置にあるが、図F7のベクトルはXZ平面において x軸から角度 $-T$ だけ回転した位置にあるということである。したがって、XZ平面上におけるベクトルの x軸からの回転角度を $\arctan 2$ を用いて求める場合には符号を変える必要があり、例えば図F7のベクトルの場合では x軸からの回転角度は -Mathf.Atan2(b, a) としてマイナスを付けなければならない。
上図F4の y軸周りの回転角度 $\varphi$ は x軸から $\boldsymbol{\mathsf{v}}'$ への回転角度であるから、$\arctan 2$ を用いて簡単に求めることができる。$\boldsymbol{\mathsf{v}}'$ は $\boldsymbol{\mathsf{v}} = (\mathsf{v_x},\ \mathsf{v_y},\ \mathsf{v_z})$ をXZ平面上に射影したベクトルであるから、$\boldsymbol{\mathsf{v}}' = (\mathsf{v_x},\ 0,\ \mathsf{v_z})$ であり、したがって $\varphi$ を度数法で求めるには以下のように計算すればよい。
// x軸から v' への回転角度 phi の計算 float radPhi = -Mathf.Atan2(v.z, v.x); float degPhi = Mathf.Rad2Deg * radPhi;
まとめると初期状態で y軸プラス方向を向いている単位ベクトル $\boldsymbol{\mathsf{v}}$ を下図F1に示される向きに向けるには、$0 \leq \theta \leq \pi$、$-\pi \leq \varphi \leq \pi$ とするとき、$\boldsymbol{\mathsf{v}}$ に対して z軸周り $-\theta$、y軸周りに $\varphi$ の順で回転を行えばよい。プログラムにすると次のようになる。
// v と y軸のなす角 theta の計算 (v は単位ベクトル) float radTheta = Mathf.Acos(v.y); float degTheta = Mathf.Rad2Deg * radTheta; Matrix4x4 Rz = GetRotation4x4(-degTheta, Vector3.forward); // x軸から v' への回転角度 phi の計算 float radPhi = -Mathf.Atan2(v.z, v.x); float degPhi = Mathf.Rad2Deg * radPhi; Matrix4x4 Ry = GetRotation4x4(degPhi, Vector3.up);
繰り返しになるが上記の角度制限の下では z軸周りの回転角度は $\theta$ ではなく $-\theta$ であること、また $\varphi$ を求める際にも $\arctan 2$ にマイナスをつけることに注意しよう。


なおここで算出される角度 $\theta$ は $\boldsymbol{\mathsf{v}}$ と y軸とのなす角であったから、$\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}'$ のなす角を $\alpha$ とすれば $\alpha = 90^\circ - \theta$ であるが(上図F8)、$\theta$ を求めずに直接 $\alpha$ を求めることも簡単にできる。図F8に示されるように $\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{v}}'$ の作る三角形 $OAB$ を考えれば、これは直角三角形であり、$|OB| = |\boldsymbol{\mathsf{v}}| = 1$、$|AB| = \mathsf{v_y}$ より、$\sin \alpha = \mathsf{v_y}$ である。したがって、$\alpha = \arcsin (\mathsf{v_y})$ とすればよい ($\sin$ の逆関数 $\arcsin$ が返す値の範囲は $-\pi/2$ ~ $\pi/2$)。
(注意 : $\arctan 2$ と似た関数に $\arctan$ という関数がある。いずれも $\tan$ の逆関数であるが、この2つの関数には重要な違いがある。 2つの関数はどちらもXY平面上において x軸からの角度を求めるものであり、その引数は $\arctan 2$ の場合は上で述べたように x座標、y座標を、$\arctan$ の場合は傾きをセットする。例えば下左図のベクトルの場合、その終点は $(a,\ a)$ であるから傾きは $1$ であり、x軸からの回転角度を求めるにはそれぞれ、$\arctan 2 (a,\ a)$、$\arctan (1)$ とすることになる。


この場合2つの関数から返される値は同じで $\pi/4\ (= 45^\circ)$ であり、確かに回転角度として正しい値が返される。しかし右図の場合はそうはいかない。右図のベクトルはその終点が $(-a,\ -a)$ であり、x軸からの回転角度は $-3\pi/4\ (= -135^\circ)$ である。$\arctan 2 (-a, -a)$ ではこの角度が返されるが、$\arctan$ の場合は傾きが左図のものと同じ $1\ (=-a/-a)$ なので $\arctan (1)$ となり、その結果 $-3\pi/4$ ではなく左図の場合と同じ $\pi/4$ が返されることになる。つまり $\arctan 2$ は $360^\circ$ に対応するが、$\arctan$ は $360^\circ$ には対応していないのである (具体的には $\arctan 2$ が返す範囲は $-\pi$ ~ $\pi$ であるが、$\arctan$ が返す範囲は $-\pi/2$ ~ $\pi/2$)。このような理由により、平面上において x軸からの角度を求める場合には $\arctan$ よりも $\arctan 2$ が使われるわけである)
D) 直線への垂線
図11には、点$P$と原点を通る直線$m$が示されている。今、点$P$から直線$m$に垂線をおろして、垂線と直線$m$の交点を$Q$とする。ここでは、この交点$Q$を内積を使って求めてみよう (2D空間の章ではある点から直線上へ垂線を下すことを「射影」と呼んだが、3D空間においても同様である。以下の点$Q$は、点$P$を直線$m$へ射影したときの像である)。

(以下では原点を$O$で表す。)
原点$O$を始点、点$P$を終点とするベクトルを$\boldsymbol{\mathsf{v}}$とする。また、直線$m$の方向(原点$O$から点$Q$へ向かう方向)を表す単位ベクトルを$\boldsymbol{u}$とし、その始点を原点に置く。ベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$のなす角を $A$とする(以上は図13参照)。


ここでベクトル$\boldsymbol{\mathsf{v}}$と単位ベクトル$\boldsymbol{u}$の内積を計算すると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}||\boldsymbol{u}|\cos{A} = |\boldsymbol{\mathsf{v}}|\cos{A}\] であるが、この $|\boldsymbol{\mathsf{v}}|\cos{A}$ が何を表すかについて図14を用いて説明しよう。
図14では原点$O$と点$P$、$Q$を結んだ三角形(直角三角形)の各辺に記号がふられてある。これは各辺の長さを表し、すなわち辺$OP$の長さが$a$、辺$PQ$の長さが$b$、辺$OQ$の長さが$c$である。ベクトル$\boldsymbol{\mathsf{v}}$は、$O$と$P$を結ぶベクトルであるから、$\boldsymbol{\mathsf{v}}$の大きさ $|\boldsymbol{\mathsf{v}}|$ は辺$OP$の長さに等しい、すなわち $|\boldsymbol{\mathsf{v}}| = a$ である。
そして、$\triangle{OPQ}$は直角三角形であるから辺$OP$と辺$OQ$の長さについて次の関係が成り立つ。
\[ a\cos{A} = c \] 以上から、
\[ |\boldsymbol{\mathsf{v}}|\cos{A} = c \] つまり $|\boldsymbol{\mathsf{v}}|\cos{A}$ は辺$OQ$の長さに等しいことがわかる。原点$O$から点$Q$の方向を表す単位ベクトルは$\boldsymbol{u}$で、原点$O$から点$Q$までの長さが $|\boldsymbol{\mathsf{v}}|\cos{A}$ であるから、点$Q$の位置は
\[ Q = (|\boldsymbol{\mathsf{v}}|\cos{A})\boldsymbol{u} \] で求められる。
E) 座標系における座標値
D)では、3D空間内の点から原点を通る直線上へおろされた垂線の足(直線との交点)を求める問題を扱った。ここで扱う内容は、その延長的な内容である。D)において垂線の足である点$Q$を求める過程を再度見直してみよう。
原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$と、直線$m$の方向を表す単位ベクトル$\boldsymbol{u}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u} = |\boldsymbol{\mathsf{v}}|\cos{A}$ は、原点$O$から点$Q$までの長さに等しいのであった。そして、原点から直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れた位置に、点$P$からの垂線の足である点$Q$はあるのであった。このことを便宜上、「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」という言い方で表す(つまり点$P$の直線$m$方向の距離とは、原点から(垂線の足)点$Q$までの距離である)。
以上をふまえて本題に入る。

点$P$の座標が$(4, 3, 2)$であるとは、点$P$を図16のように原点に置いてから、まず始めにx軸方向に$4$移動させ(図17)、次にy軸方向に$3$移動させ(図18)、そして最後にz軸方向に$2$移動させる(図15)、この原点からの3回の移動後の$P$の位置のことを意味している。
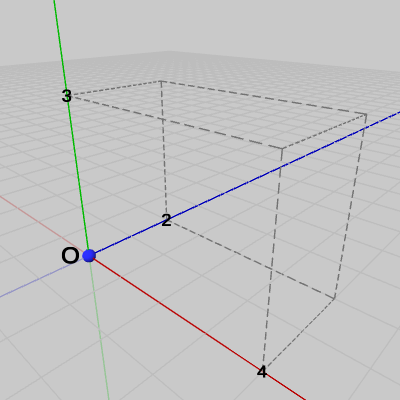 図16 点P = (0, 0, 0)
図16 点P = (0, 0, 0)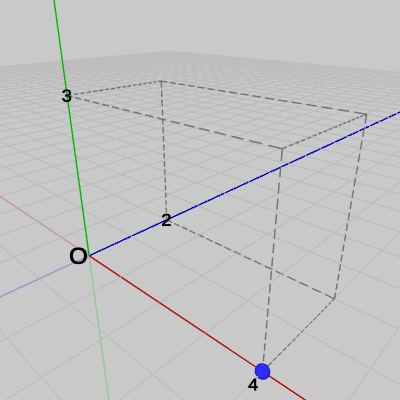 図17 (0, 0, 0)からx軸方向に4移動 (点Pは(4, 0, 0)に移動する)
図17 (0, 0, 0)からx軸方向に4移動 (点Pは(4, 0, 0)に移動する)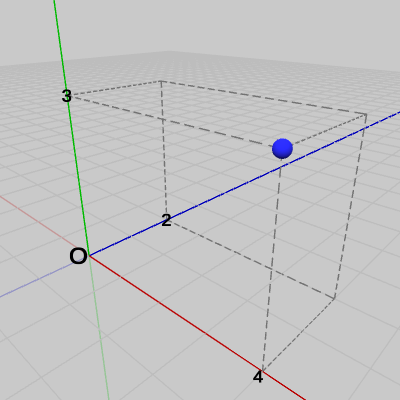 図18 (4, 0, 0)からy軸方向に3移動 (点Pは(4, 3, 0)に移動する)
図18 (4, 0, 0)からy軸方向に3移動 (点Pは(4, 3, 0)に移動する)
言い換えれば、点の座標値における各座標(x座標、y座標、z座標)は、その点が原点から各軸の方向にどれだけ離れているかを表している。点$P = (4, 3, 2)$の場合でいえば、点$P$が原点からx軸方向に$4$、y軸方向に$3$、z軸方向に$2$だけ離れていることを表している。
点$P$が原点からx軸方向、y軸方向、z軸方向にどれだけ離れているかは図15を見ればわかるが、ここでは内積を使ってその距離を計算してみよう。
そのために原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と、x軸、y軸、z軸の各方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$、$\boldsymbol{u_y} = (0, 1, 0)$、$\boldsymbol{u_z} = (0, 0, 1)$を用意する(図19、図20)。


まず、点$P$が原点からx軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とx軸方向を表す単位ベクトル$\boldsymbol{u_x} = (1, 0, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_x}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} = 4\cdot1 + 3\cdot0 + 2\cdot0 = 4\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \]

点$P$からx軸へ垂線をおろし、その足を点$Q_x$とする($\triangle{OPQ_x}$は直角三角形になる)。D)で見たように、原点$O$から点$Q_x$までの距離は、原点$O$と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$とx軸方向の単位ベクトル$\boldsymbol{u_x}$の内積 $\boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_x} (= |\boldsymbol{\mathsf{v}}|\cos{A})$ であるが、これは上で求めたとおり $4$ である。
先程、D)の点$P$について次のような言い方を用いた。「点$P$は直線$m$の方向に$|\boldsymbol{\mathsf{v}}|\cos{A}$だけ離れている」。この表現を今の例にあてはめると、直線$m$はx軸に相当し、ここでの$|\boldsymbol{\mathsf{v}}|\cos{A}$は$4$であるので、「点$P$はx軸の方向に$4$だけ離れている」という内容になる。
点$P$が原点からx軸方向にどれだけ離れているかを内積を使って求めるというのが、ここでの目的であったが、今述べてきたことがそれにあたるわけである。
点$P$のy軸方向の距離、z軸方向の距離についても同様の手順で求めることができる。


図22に示されるようにy軸方向の距離は、点$P$からy軸におろした垂線の足を点$Q_y$とすれば、原点から$Q_y$までの距離のことである($\triangle{OPQ_y}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とy軸方向を表す単位ベクトル$\boldsymbol{u_y} = (0, 1, 0)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_y}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_y} = 4\cdot0 + 3\cdot1 + 2\cdot0 = 3\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \] x軸の場合と同様に、この結果は「点$P$はy軸の方向に$3$だけ離れている」ことを意味している。
図23に示されるようにz軸方向の距離は、点$P$からz軸におろした垂線の足を点$Q_z$とすれば、原点から$Q_z$までの距離のことである($\triangle{OPQ_z}$は直角三角形になる)。したがって、ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とz軸方向を表す単位ベクトル$\boldsymbol{u_z} = (0, 0, 1)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_z}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_z} = 4\cdot0 + 3\cdot0 + 2\cdot1 = 2\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \] この結果は「点$P$はz軸の方向に$2$だけ離れている」ことを意味している。
だが、以上に述べてきた事柄はおそらく自明過ぎるものであろう。x軸、y軸、z軸のような基本的な座標軸上での点の位置は、そもそも点の座標値から分かることであって、わざわざ内積を使ってまで求める必要はない。確かに今まで用いてきた座標系(と座標値)ならばそれはいえる。しかし、例えばこの同じ点$P$を図24に示されるような水色、紫色、黄色の座標軸を持つ傾いた座標系を基準にした場合などでは、いささか状況が異なってくる。


図24に示される座標系は互いに直交する i軸(水色)、j軸(紫色)、k軸(黄色)によって構成される座標系で、便宜上ここでは ijk座標系と呼ぶことにする(図25はやや離れた位置から ijk座標系を見たもの。また、i軸、j軸、k軸についてはプラス側のみ表示してある)。そして、今まで用いてきた x軸、y軸、z軸の座標系の方をxyz座標系と呼ぶことにする。
図からわかる通り ijk座標系は傾いた座標系であり、xyz座標系とは原点が一致している。
今から問題とするのは、上で使ってきた点$P$の ijk座標系における座標値の計算である。すなわち、点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離を求めることであり、それは図26における点線の直方体の3つの辺の長さ$a$、$b$、$c$を求めることと同じである(図27は見やすくするためにxyz座標系を取り除いたもの。図における点線の図形は直方体であるので隣接する面の間の角度は直角である)。


xyz座標系における$P$の座標は$(4, 3, 2)$であったが、ijk座標系での座標は図27を見ると、そのような整数値でないことは明らかである(もちろん点$P$の位置は今までの位置から動かしていない)。
しかし、点$P$の ijk座標系における座標を計算するのは難しいことではない。今まで見てきたことをなぞっていけば、自ずと答えが導かれる。ただし、注意すべきことが1つある。今、座標系が2つ出てきたが、この先で使用する、原点と点$P$を結ぶベクトル$\boldsymbol{\mathsf{v}}$、i軸、j軸、k軸の方向を表す単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$などは全てxyz座標系での値である。例えば、何度も出てきたが$(4, 3, 2)$という点$P$の座標はxyz座標系での値である。ijk座標系では図26(あるいは図27)に示されるように点$P$は$(a, b, c)$であり、$(4, 3, 2)$ではない (これは 点$P$の i軸方向の距離、j軸方向の距離、k軸方向の距離が $a$、$b$、$c$ であり $4$、$3$、$2$ ではないことを意味する)。
計算手順については今までと同様である。
まず、原点$O$から点$P$へのベクトル$\boldsymbol{\mathsf{v}}$を用意する(図28)。xyz座標系での値であるので、今までどおり、$\boldsymbol{\mathsf{v}} = (4, 3, 2)$である。また、i軸方向、j軸方向、k軸方向の単位ベクトルを$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$とする(図29。図からわかるようにこれらもxyz座標系での値であり、小数3位以下を省略してある)。
図の緑色の数値はベクトルの内容を表している。


(以下で使用される単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$は小数第3位以下を省略した値であるため、それらを使った計算結果もわずかな誤差を含んでいる。)
では、点$P$が原点から i軸方向にどれだけ離れているかを計算する。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と i軸方向を表す単位ベクトル$\boldsymbol{u_i} = (0.94, 0.12, 0.31)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_i}$のなす角を$A$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_i} = 4\cdot0.94 + 3\cdot0.12 + 2\cdot0.31 = 4.74\quad(= |\boldsymbol{\mathsf{v}}|\cos{A}) \]
この値が表すのは、図30に示されるように点Pから i軸におろした垂線の足を点$Q_i$とすれば、原点から$Q_i$までの距離のことである($\triangle{OPQ_i}$は直角三角形になる)。図30はxyz座標系でこの状況を示したものだが、図31のように ijk座標系のみで表示すると上の計算で何を求めたのかがより明らかになるだろう。原点から$Q_i$までの距離は、すなわち点$P$の i軸方向の距離のことであり、図31に示される辺の長さ$a$に等しい。つまり、点$P$の ijk座標系での i座標は $a = 4.74$ である。

点$P$が原点から j軸方向にどれだけ離れているかについても同様に計算してみよう。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$と j軸方向を表す単位ベクトル$\boldsymbol{u_j} = (0.02, 0.91, -0.42)$の内積は、$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_j}$のなす角を$B$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_j} = 4\cdot0.02 + 3\cdot0.91 + 2\cdot(-0.42) = 1.97\quad(= |\boldsymbol{\mathsf{v}}|\cos{B}) \]
この値が表すのは、図32に示されるように点Pから j軸におろした垂線の足を点$Q_j$とすれば、原点から$Q_j$までの距離のことである($\triangle{OPQ_j}$は直角三角形になる)。図33はこの様子を ijk座標系のみで表示したものである。原点から$Q_j$までの距離は、すなわち点$P$の j軸方向の距離のことであり、図33に示される辺の長さ$b$に等しい。つまり、点$P$の ijk座標系での j座標は $b = 1.97$ である。

点$P$のk軸方向の距離についても同様の手順を繰り返せばよい。
ベクトル$\boldsymbol{\mathsf{v}} = (4, 3, 2)$とk軸方向を表す単位ベクトル$\boldsymbol{u_k} = (-0.34, 0.40, 0.85)$の内積は、
$\boldsymbol{\mathsf{v}}$と$\boldsymbol{u_k}$のなす角を$C$とすると、
\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_k} = 4\cdot(-0.34) + 3\cdot0.40 + 2\cdot0.85 = 1.54\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \]
この値が表すのは、図34に示されるように点Pからk軸におろした垂線の足を点$Q_k$とすれば、原点から$Q_k$までの距離のことである($\triangle{OPQ_k}$は直角三角形になる)。図35はこの様子を ijk座標系のみで表示したものである。原点から$Q_k$までの距離は、すなわち点$P$のk軸方向の距離のことであり、図35に示される辺の長さ$c$に等しい。つまり、点$P$の ijk座標系でのk座標は $c = 1.54$ である。\[ \boldsymbol{\mathsf{v}}\cdot\boldsymbol{u_k} = 4\cdot(-0.34) + 3\cdot0.40 + 2\cdot0.85 = 1.54\quad(= |\boldsymbol{\mathsf{v}}|\cos{C}) \]


以上の結果をまとめると、点$P$の ijk座標系における座標(i座標、j座標、k座標)は、
\[P = (4.74,\ 1.97,\ 1.54)\]であることがわかった(図36)。
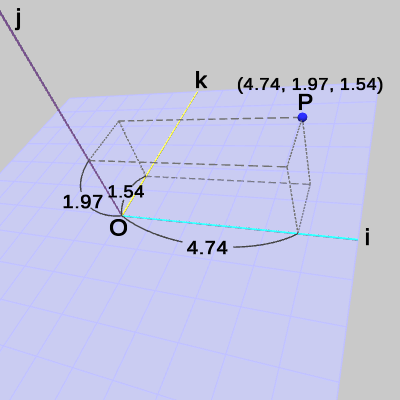 図36 ijk座標系における点P = (4.74, 1.97, 1.54)
図36 ijk座標系における点P = (4.74, 1.97, 1.54) 図37 xyz座標系における点P = (4, 3, 2)
図37 xyz座標系における点P = (4, 3, 2)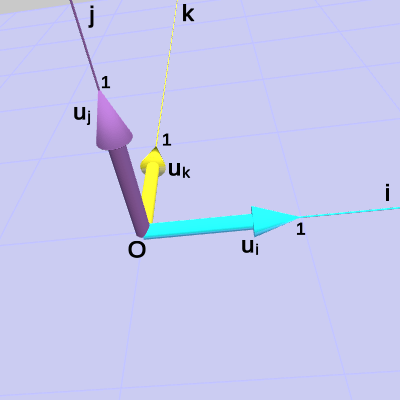 図38 ijk座標系における単位ベクトルui, uj, uk
図38 ijk座標系における単位ベクトルui, uj, uk
比較のために図37にxyz座標系での点$P$を示す。
また、今までの計算で使われてきた単位ベクトル$\boldsymbol{u_i}$、$\boldsymbol{u_j}$、$\boldsymbol{u_k}$の値はxyz座標系での値であったが参考のために ijk座標系での値を以下に示しておこう(図38参照。以下のカッコの中の数値は i座標、j座標、k座標の順である)。
\begin{align*}\boldsymbol{u_i} = (1, 0, 0) \\\boldsymbol{u_j} = (0, 1, 0) \\\boldsymbol{u_k} = (0, 0, 1) \\\end{align*}
最後に、本節で述べた内容に関してのプログラムを作成する。
# Code1
最初のプログラムでは、2つのベクトルを単位ベクトル化してそれらの内積を求める。Unityで内積を求める場合には次のメソッドが用意されている。
Vector3.Dot(Vector3 v1, Vector3 v2)
: 引数に指定される2つのベクトルの内積を計算する Vector3構造体のstaticメソッド (戻り値は float型)。[Code1] (実行結果 図39)
Vector3 v1 = new Vector3(1.77f, 0.80f, -0.48f); Vector3 v2 = new Vector3(-2.06f, 5.45f, 1.45f); float dot = Vector3.Dot(v1.normalized, v2.normalized); Debug.Log(dot); v1 = new Vector3(3.17f, -1.29f, -2.07f); v2 = new Vector3(-3.97f, 1.61f, 2.59f); dot = Vector3.Dot(v1.normalized, v2.normalized); Debug.Log(dot);

第2の計算は v1、v2の値を変えて、再び単位ベクトルの内積を計算したものである。
実行結果は -0.9999... となっており、今度は非常に$-1$近いに値である。「ベクトルのなす角」で見たように、2つのベクトルの単位ベクトルの内積が$-1$であるときは、その2つのベクトルは平行であるが、向きは反対である。したがって、第2の計算における v1、v2のなす角は非常に$180$°に近いということがわかる。
# Code2
では次に、図40に示される$\triangle ABC$内の$\angle T$を求める問題について考える。各点の座標は $A = (2.77,\ 5.0,\ 2.36)$、$B = (3.05,\ 4.41,\ 4.25)$、$C = (2, 5, 3)$ である。


まず先にプログラムを示す。
[Code2] (実行結果 図42)
Vector3 A = new Vector3(2.77f, 5.0f, 2.36f); Vector3 B = new Vector3(3.05f, 4.41f, 4.25f); Vector3 C = new Vector3(2.0f, 5.0f, 3.0f); Vector3 vB = B - A; Vector3 vC = C - A; float dot = Vector3.Dot(vB.normalized, vC.normalized); float radian = Mathf.Acos(dot); float deg = radian * Mathf.Rad2Deg; Debug.Log(deg);

7行目の Acos(..) は $\cos$ 関数の逆関数で、$\cos\theta$ から $\theta$ を求める際に使用する。6行目のdotは $\cos T$ に等しいので、7行目の Acos(dot) によって返される値は角度 $T$ である。しかし、ここで注意することがある。Acos(..) から返される角度は弧度法の値($\pi / 2$、$\pi$ などで単位はラジアン)になっているという点である。
8行目では7行目で算出された radian に Mathf.Rad2Deg を掛けているが、これによって弧度法の値から度数法の値($30^\circ$、$60^\circ$ など)に変換されるのである (Mathf.Rad2Degは、弧度法の値から度数法の値に変換するときに、弧度法の値に掛ける定数)。
実行結果(図42)では 60.23... と出力されているが、これは $\angle T$ が約 $60^\circ$ であることを示している。
# Code3
プログラミングにおいては処理を効率化するためのテクニックが数多くあるが、その基本的なものの1つに「平方根を使わない」というものがある。例えばベクトルの大きさを比較する際、2つのベクトル $\boldsymbol{\mathsf{v}_1} = (x_1,\ y_1,\ z_1)$、$\boldsymbol{\mathsf{v}_2} = (x_2,\ y_2,\ z_2)$ の大きさは\[ |\boldsymbol{\mathsf{v}_1}| = \sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2} \qquad ,\qquad |\boldsymbol{\mathsf{v}_2}| = \sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2}\]として求められるが(3-1節)、2つのベクトルの大きさの比較においては平方根を使っても使わなくても大小関係は同じである。$|\boldsymbol{\mathsf{v}_1}|$、$|\boldsymbol{\mathsf{v}_2}|$ の例でいえば $|\boldsymbol{\mathsf{v}_1}| < |\boldsymbol{\mathsf{v}_2}|$ であることは\[ \sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2} < \sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2} \tag{1}\]を意味するが、この場合は平方根を取った以下の式も成り立つ。\[ {x_1}^2 + {y_1}^2 + {z_1}^2 < {x_2}^2 + {y_2}^2 + {z_2}^2 \tag{2}\]つまり (1) が成り立つならば (2) が成り立ち、逆に (2) が成り立つ場合でも (1) は成り立つから、結局2つのベクトルの大きさを比較する際には平方根を使う必要はないのである。
実際のコードでは次のように書くよりも
// v1, v2 の大きさの比較
if(v1.magntude < v2.magnitude)
{ ... }
// v1, v2 の大きさの比較 (2乗で比較)
if(v1.sqrMagntude < v2.sqrMagnitude)
{ ... }
あるいはコンピューターグラフィックスのプログラムではこの2乗の比較は次のように書かれることもある。
// v1, v2 の大きさの比較 (2乗で比較)
if(Vector3.Dot(v1, v1) < Vector3.Dot(v2, v2))
{ ... }
今回作成するプログラムもこの「平方根を使わない」ことに関連するものであるが、このプログラムは読者用の課題である。
ともに始点が $A$ の2つのベクトル $\overrightarrow{AB}$、$\overrightarrow{AC}$ が適当な位置に置かれている (図43)。この2つのベクトルの大きさはそれぞれ異なり、2つともその大きさは $1$ ではない。


ここでベクトル $\overrightarrow{AC}$ に直交するベクトルを求めるとする。その場合図44のように $\overrightarrow{AC}$ の延長上に点 $D$ を、三角形 $ABD$ が直角三角形になるように置けば、ベクトル $\overrightarrow{DB}$ が求めるベクトルである。
ここでの課題は $\overrightarrow{AC}$ と直交する上記のベクトル $\overrightarrow{DB}$ を求めることであるが、このベクトルを求める際には平方根を使わずに求めるものとする。平方根を使わないということは magnitude や normalized のようなプロパティ、あるいは Normalize() のようなメソッドも使うことはできない (ただし上記の sqrMagnitude を使うことは問題ない)。
このプログラムには次の定数が用意されている。
A, B, C
: 上図の2つのベクトル $\overrightarrow{AB}$、$\overrightarrow{AC}$ の始点と終点を表す (Vector3型)。プログラムはCode3に作成するものとする。
[Code3] (実行結果 図45)
if (!i_INITIALIZED)
{
Vector3 vDB = Vector3.zero;
Debug.Log(vDB);
i_INITIALIZED = true;
}

特に直接的な影響はないので答えから先にいえば、正しく計算が行われた場合出力される vDB の値は $(2, 3, 4)$ という値になる。
(解答例のプログラムは Sec304_Ans.txt を参照 ; Sec304_Ans.txtはダウンロードコンテンツ内の「txt_ans」フォルダに含まれている)。
# Code4
このプログラムも読者用の課題である。下左図の2つのベクトル $V_1$、$V_2$ は同じ大きさのベクトルであり、$V_1$ は x軸プラス方向を向いている。この状態から $V_1$ を適当に回転させて $V_2$ に重ねる回転を考えよう。


そのためには下図のように、まず $V_1$ を z軸周りに回転させ、続いて y軸周りに回転させれば目的の状態にすることができる。この回転における z軸周りの回転角度を $\alpha$、y軸周りの回転角度を $\beta$ とする。

ここでの課題はこの2つの回転角度 $\alpha$ 及び $\beta$ を求めることである ($\alpha$、$\beta$ は弧度法ではなく度数法の角度)。
上記の解説では同様の問題を扱ったが、そこではベクトルの初期状態の向きは y軸プラス方向であった。この課題の場合は初期状態が x軸プラス方向であるが、考え方は同じである。上で述べた手続きをそのまま適用すればよい。
プログラムには以下の定数が用意されている。
u2
: 上図の $V_2$ の方向を表す単位ベクトル (Vector3型)。プログラムはCode4に作成するものとし、$V_1$ の回転は S キーが押された際に行われるものとする。
[Code4] (実行結果 図47)
if (Input.GetKeyDown(KeyCode.S))
{
float alpha = 0;
float beta = 0;
RotateV1(alpha, beta);
}
if (Input.GetKeyDown(KeyCode.C))
{
Reset();
}
4行目の alpha に z軸周りの回転角度 $\alpha$ を、5行目の beta に y軸周りの回転角度 $\beta$ をセットするだけでよい。最初の段階ではいずれも $0$ がセットされているが、この場合には S キーを押しても何も変化しない。alpha、beta に適切な値がセットされていれば S キーが押されると図46の状態から図47の状態になる (最初の状態に戻すには C キーを押せばよい)。
回転角度を求める際にはその符号に注意しなければならない。前節で見たように(左手系の場合には)左手の親指を回転軸に向けたときの残りの指の曲がっている方向が回転のプラス方向、つまり回転角度の符号をプラスにする回転である。
上の解説でも述べたことであるが弧度法から度数法の変換について再度触れておこう。
角度を求める逆関数 Asin、Acos、Atan2 は弧度法の角度($\pi/4$、$\pi/2$ など)で返されるので、それを度数法の角度($45^\circ$、$90^\circ$ など)に変換するためにはUnityに用意されている定数 Mathf.Rad2Deg を以下のように使用する。
// 弧度法から度数法の角度への変換 float radian = Mathf.Asin(val); float degree = Mathf.Rad2Deg * radian;
(解答例のプログラムは Sec304_Ans.txt を参照)
© 2020-2025 Redpoll's 60 (All rights reserved)