Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-14
第3章 3D空間の基礎
$§$3-14 オイラー角 1
本節では3Dコンピュータグラフィックスにおいて回転を扱う際に、回転の指定方法としてよく用いられるオイラー角(Euler angles)について解説する。
今までに見てきた回転行列は、回転軸と角度を指定して得られるものであった。オイラー角によって回転行列を取得する場合には、次の3つの角度、すなわち x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度が必要になる。この3つの角度をもとにして回転行列を計算するわけであるが、このときに重要なのが回転の順序である。
オイラー角による回転は x軸周りの回転、y軸周りの回転、z軸周りの回転を合成したものである。例えば x軸周りに回転させ、次にy軸周りの回転、最後にz軸周りの回転の順で行うのか、あるいは、まず z軸周りに回転させ、次にy軸周りの回転、最後にx軸周りの回転の順で行うのかといったように回転の順序をあらかじめ決めておかなければならない。順序のパターンはいくつかあるが、どういった順序で回転を行うかは、使用しているゲームエンジンやDCCツールによって異なる。Unityの場合は、Z-X-Yの順序である。すなわち、まず z軸周りの回転、次にx軸周りの回転、最後にy軸周りの回転の順で行われる。
オイラー角による回転は3つの軸の周りの回転の合成なので、3つの変換行列の積で表される。
x軸周りの回転行列を $R_x$、y軸周りの回転行列を $R_y$、z軸周りの回転行列を $R_z$ とするときの Z-X-Yオーダーのオイラー角による回転行列 $R_{zxy}$ は
\[ R_{zxy} = R_yR_xR_z \]である。
行列の成分までを具体的に示せば(それぞれの軸における回転角度を $X$、$Y$、$Z$ とする)
プログラムで使用する場合には以下のように記述される (同次座標に対応させるため $4\times 4$ 行列として作成している)。
上記の計算をそのまま実装したものである。引数の eulX、eulY、eulZ は各軸の回転角度であるが、これは度数法で表されているため Mathf.Sin(..) や Mathf.Cos(..) などの引数として使うためには弧度法による角度に変換しなければならない (4~6行目)。
では以下で、オイラー角を可視化した使用例を見ていく。この講義において用いられるオイラー角の回転順序は一部を除きすべてUnityと同じく Z-X-Yオーダーである。
なお細かいことではあるが1点追記する。オイラー角による回転には、回転軸を固定して考える回転と、回転軸をオブジェクトと一体化して考える回転の2つに分かれる。前者を extrinsic rotations、後者を intrinsic rotations という。Unityに用意されているQuaternion構造体のstaticメソッド Quaternion.Euler(x, y, z) は、オイラー角による回転を表すQuaternionを取得するメソッドであるが、このメソッドから返されるQuaternionを使用して確認する限りでは、Unityにおけるオイラー角回転は回転軸固定の extrinsic rotations である。したがって、この講義においてもオイラー角回転は extrinsic rotations によるものとして進めていく。ただし、オイラー角回転といえば intrinsic rotations を指すことが普通である (intrinsic rotations については次節を参照)。
より詳しくいえば、extrinsic rotations とはオブジェクトの親座標系のx軸、y軸、z軸を回転軸とする回転であり、intrinsic rotations とはオブジェクトのローカル座標系のx軸、y軸、z軸を回転軸とする回転である (オブジェクトの親座標系やローカル座標系については4-8節で解説する)。
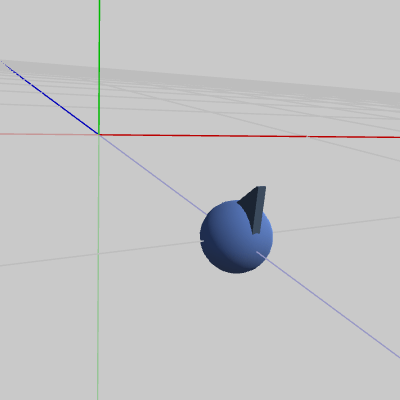
図1 FinBall 初期状態 (z = -1) 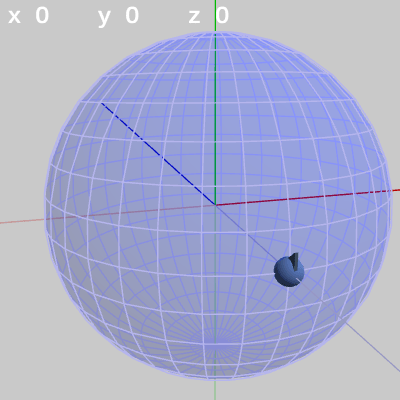
図2 FinBallと単位球面(半径1)
図1のオブジェクトFinBallは、初期状態で $(0,\ 0, -1)$に置かれている上部に突起のついた球である。図2は半径1の球面とFinBallをやや離れた位置から見たものである。球面の半径は $1$なので、初期状態のFinBallは図のように球面上の$(0,\ 0, -1)$にある。上の白い数字はそれぞれ x軸、y軸、z軸周りの回転角度であり、この3つの角度をもとにしてオイラー角による回転行列を計算し、それをFinBallに実行する。この数字はFinBallの初期状態ではすべて $0$であるが、これはFinBallに何も回転が実行されていないことを示している。
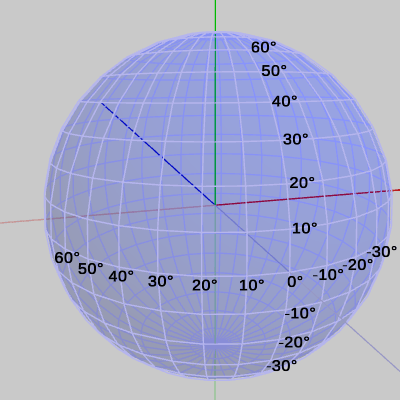
図3 緯度、経度 (球面上の 0°は緯度、経度がともに0°であることを示しており、その座標は (0, 0, -1) である) 以下では便宜上、地球と同じように球面上の縦方向の線を経線、横方向の線を緯線と呼ぶことにする。また、経線上の(縦方向の)位置を緯度、緯線上の(横方向の)位置を経度という呼び方を用いる(図3において縦方向に並んだ数値が緯度であり、横方向に並んだ数値が経度である)。
緯度、経度の起点(すなわち $0$°の位置)はFinBallの初期状態の位置である $(0,\ 0, -1)$とする。本節及び次節で使われる図においては、$0$° は常に緯度、経度ともに$0$°の位置であることを示している。
度数の増減は $(0,\ 0, -1)$を起点としてプラス、マイナスで表記する。以下は図3を参考に説明する。
緯度に関しては、経線上(縦方向の線)で起点より上側はプラスの値であり、上に進むにつれて増加する。経線上で起点より下側はマイナスの値であり、下に進むにつれて減少する(緯度$90$°、$-90$°は、地球でいえば北極点、南極点である)。また、ある経線上の緯度$180$°と$-180$°は同じ地点である。
経度に関しては、緯線上(横方向の線)で起点より左側はプラスの値であり、左に進むにつれて増加する。緯線上で起点より右側はマイナスの値であり、右に進むにつれて減少する。また、ある緯線上の経度$180$°と$-180$°は同じ地点である。
なお、x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度については単に x-角度、y-角度、z-角度と表記する。
これらの用語を用いて、可視化されたオイラー角の回転について解説する。
本節のアニメーションは、次のコードにおけるオイラー角の数値を変えてFinBallに実行した結果である。
TH3DMath.GetEulerRotation4x4(..)はカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。i_eulX、i_eulY、i_eulZは、それぞれ x-角度、y-角度、z-角度を表すインスタンス変数で、図の白い数字はこれらの値を表したものである。取得される回転行列R_zxyは、上で述べたようにz軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
次の図4はx-角度だけを$10$°ずつ増減させたもの、図5はy-角度だけを$10$°ずつ増加させたもの、図6はz-角度だけを$10$°ずつ増減させたものである。
x-角度だけを変える場合、FinBallは縦方向の線、つまり経線上を動く(図4)。
y-角度だけを変える場合、FinBallは横方向の線、つまり緯線上を動く(図5)。
z-角度だけを変える場合は、FinBallの球面上での位置の変化は起こらない。この場合のFinBallはその場所において図6に示される回転を行うが、本節及び次節では図6のような回転を「Roll回転」と呼ぶことにする。
次の図は、y-角度を左から $y = 50$°、$y = 140$°、$y = -20$°に固定して、x-角度だけを変化させたものである。
y-角度を$50$°に固定して、x-角度だけを変化させる場合は、経度$50$°の経線上を動く(図7)。
y-角度を$140$°に固定して、x-角度だけを変化させる場合は、経度$140$°の経線上を動く(図8 ; 経度$140$°は球面の裏側の経線)。
y-角度を$-20$°に固定して、x-角度だけを変化させる場合は、経度$-20$°の経線上を動く(図9)。
次の図は、x-角度を左から $x = -30$°、$x = 20$°、$x = 60$°に固定して、y-角度だけを変化させたものである。
x-角度を$-30$°に固定して、y-角度だけを変化させる場合は、緯度$-30$°の緯線上を動く(図10)。
x-角度を$20$°に固定して、y-角度だけを変化させる場合は、緯度$20$°の緯線上を動く(図11)。
x-角度を$60$°に固定して、y-角度だけを変化させる場合は、緯度$60$°の緯線上を動く(図12)。
次の図は、x-角度、y-角度を左から $(x = 20^\circ,\ y = 40^\circ)$、$(x = 10^\circ,\ y = 10^\circ)$、$(x = 30^\circ,\ y = -140^\circ)$に固定して、z-角度だけを変化させたものである (図13に表示されているFinBallから原点へ向けられている青い矢印は この回転の回転軸である)。
z-角度だけを変化させる場合は、球面上のどの地点においても、その場所でRoll回転をするのである。たとえば、図13の場合は x-角度 $20$°、y-角度 $40$° であるが、このときにz-角度を変化させると球面上の緯度$20$°、経度$40$°の位置でRoll回転を行うことになる。Roll回転とは、FinBallの場合では図13に示されるように原点と球の中心を結ぶ軸周りの回転となる (オブジェクトの初期状態でオブジェクトの中に原点が含まれる場合は、Roll回転は原点を通りオブジェクトを貫通する軸周りの回転となる。「オブジェクトを貫通する軸」は状況によって変化するが、Z-X-Yオーダーにおいてx-角度、y-角度を変化させていない $0$°のままの状態では、Roll回転はz軸周りの回転と同じである。具体例については次節参照)。
以上をまとめると、オブジェクトが初期状態でz軸上(の原点以外の位置)に置かれている場合、Z-X-Yオーダーのオイラー角による回転行列をオブジェクトに実行すると、オブジェクトから原点までの距離を半径とする球面上を オブジェクトは運動することになる。
具体的には、x-角度を変化させるとオブジェクトがどこにいても、その位置から縦方向、すなわち経線上を動き、y-角度を変化させるとオブジェクトがどこにいても、その位置から横方向、すなわち緯線上を動く。z-角度を変化させる場合はオブジェクトがどこにいても、その位置でRoll回転を行う。
ここで使用している FinBallの場合でいえば、x-角度、y-角度、z-角度が「x 60 y 120 z -30」であるとき、FinBallは単位球面上において 緯度$60$°、経度$120$°の位置にあり、その位置において$-30$°のRoll回転がなされていることを意味する。
このように、オイラー角による回転は指定された3つの角度から結果をイメージしやすいのである。
オブジェクトが初期状態で、図16のように原点に置かれている場合でも、上記のような球面上でオブジェクトを運動させることは、オイラー角を用いることによって簡単に実現できる。
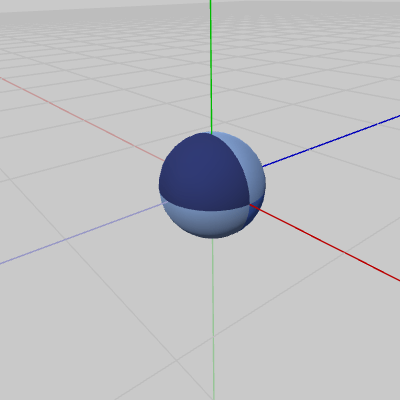
図16 Sphere 初期状態 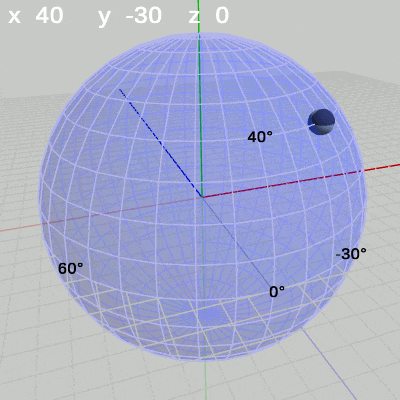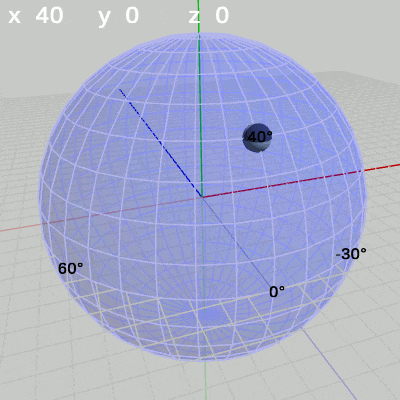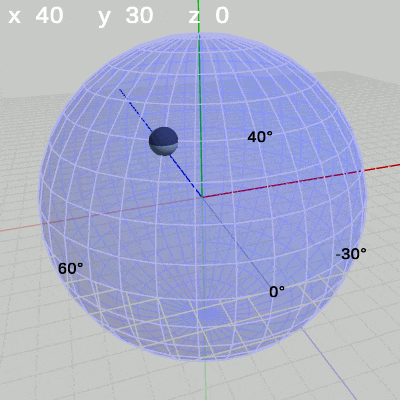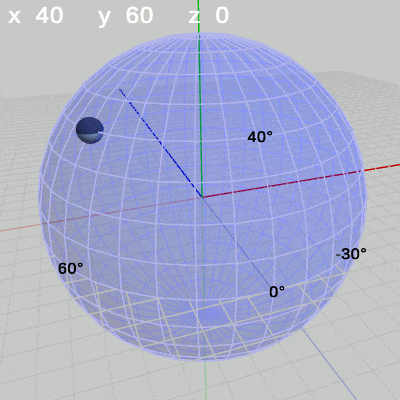
図17 半径8の球面上を移動
図16のオブジェクトSphereの初期状態での位置は原点であるが、仮に初期状態での位置が$(0, \ 0, -8)$であったとしよう。その場合は、Sphereに対してオイラー角による回転行列を実行すると、上で述べたように$(0, \ 0, -8)$から原点までの距離を半径とする球面、すなわち半径$8$の球面上をSphereは運動することになる。この場合の球面上でのSphereの位置は、Sphereに実行したものとおなじ回転行列を$(0, \ 0, -8)$に掛ければ求められる。
結局、Sphereが初期状態で原点にある場合でも、半径$r$ の球面上の緯度$a$、経度$b$の地点に移動させるためには、オイラー角のx-角度、y-角度を $a$、$b$とした回転行列を求めて、それを$(0, \ 0, -r)$に掛けて球面上の緯度$a$、経度$b$の地点の座標値を算出し、その座標の位置にSphereを移動させればよい。コードで表すと次のようになる。
初期状態で原点に置かれているSphereを半径$r$ の球面上の緯度$a$、経度$b$の位置に移動させる処理(ただし緯度、経度の起点は $(0, \ 0, -r)$ とする ; また、以下のコードから分かるように Shepreは球面上の指定された緯度、経度の位置へ移動するが、Spehreの向きは初期状態から変わらない。Spehreに実行される変換は平行移動だけである)。
4行目の SetLocalPosition(Vector3 v) は、引数に指定されたベクトル分移動させるカスタムライブラリーのメソッドである。2行目で計算されるオイラー角による回転行列は$4\times4$行列なので$(0, \ 0, -r)$を表すpos0も同次座標になっている。3行目では$4\times4$行列と4次元ベクトルの積の結果をVector3型にセットしているが、これは左辺をVector3型にすることによってUnityでは、$4\times4$行列と4Dベクトルの積のw座標が自動的に取り除かれてセットされるのである。
例えば図16のオブジェクトSphererを半径$8$の球面上の緯度$40$°の緯線上で、経度$-30$°から$60$°まで毎フレーム$10$°ずつ移動させるプログラムは以下のようになる(実行結果 図17 ; 3行目のi_eulYのここでの初期値は$-30$)。
今まで見てきたとおり、z軸上のある地点を起点とすれば、その起点から原点までの距離を半径とする球面において、オイラー角のx-角度、y-角度は、球面上の緯度、経度にそのまま対応している。x-角度、y-角度の数値を見れば、オブジェクトが球面上のどの位置にいるかを容易にイメージすることができる。これがオイラー角の球面上における可視化である。
FinBallがオイラー角による回転によって図18に示される状態になったとする (初期状態での位置は図2と同じ $z=-1$ である)。
図18に示されるように、この状態においての x-角度、y-角度、z-角度はそれぞれ $30$°、$-70$°、$20$°である (すなわち 緯度$30$° 経度$-70$° の位置にあり、$20$°のRoll回転がなされている)。今 この状態からオイラー角の x-角度を$50$°増加させるとしよう。上で述べてきたように、x-角度の増減によって FinBallは経線上を動くことになる。したがって、このときに FinBallに起こる変換は図18の位置から経線上を$50$°分動くことになる。図19は x-角度を$50$°増加させたときの様子である。
Z-X-Yオーダーのオイラー角による回転の場合は、x-角度を変化させることと x軸周りに回転を行うことは必ずしも同じではない (同じである場合もある)。例えば、図20は 図18の状態から FinBallを x軸周りに$50$°回転させたときの様子であるが、この結果は明らかに、図18の状態から x-角度を$50$°増加させた結果である図19とは異なる結果となっている。同様のことは z-角度についてもいえる。すなわち、Z-X-Yオーダーのオイラー角による回転の場合は、z-角度を変化させることと z軸周りに回転を行うことは必ずしも同じではない (同じである場合もある)。しかし、Z-X-Yオーダーの場合は y-角度を変化させることと y軸周りの回転は同じ結果になる (つまり、y-角度を変化させると常にy軸周りの回転になる)。
x-角度を$50$°増加させると、その時にいる位置から経線上を$50$°分動いた位置に移る結果になったが、以下ではこの変換過程を順を追って見ていこう。まずは、x-角度を$50$°増加させる前の状態 「x 30 y -70 z 20」 になる過程から始める。
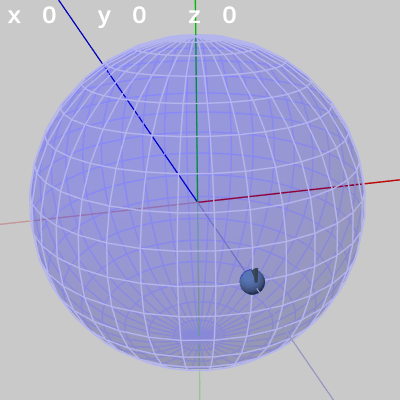
図21 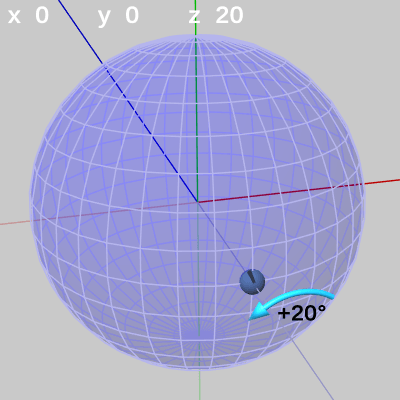
図22

図23 
図24
図21は FinBallの初期状態であり $z = -1$ に位置している。図22は Z-X-Yオーダーの最初の回転である、z軸周りの回転が行われたときの様子である。ここではz軸周りに$20$°の回転である。図23は第2の回転である x軸周りの回転が行われたときの様子であり、第1の回転後の位置からx軸周りに$30$°の回転が行われている。図24は第3の回転である y軸周りの回転が行われたときの様子である。第2の回転後の位置からy軸周りに$-70$°の回転が実行される。図24は、この3つの回転すべてが実行されたときの状態でもあり、先程の図18の状態と同じものである。
Z-X-Yオーダーのオイラー角による回転で、それぞれの角度が「x 30 y -70 z 20」という値であることは、オブジェクトに対して 今述べた3つの回転が指定の順序で実行されていることを意味している。
では次に、この状態から x-角度を$50$°増加させる。このとき、それぞれの角度は「x 80 y -70 z 20」となり、FinBallは図19に示される状態になるが、これもまた Z-X-Yオーダーの回転の結果なのである。以下の図はこの状態に至るまでの変換過程である。

図21 
図22

図25 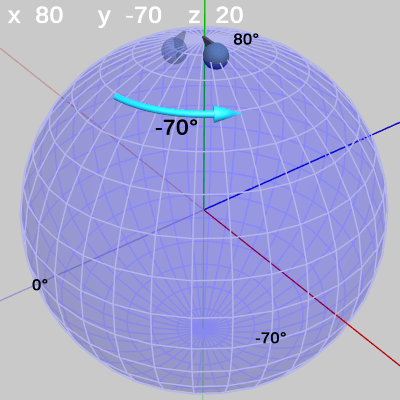
図26
図21、図22は先程と同様にそれぞれ FinBallの初期状態、及び z軸周りの$20$°の回転である。
図25は第2の回転である x軸周りの回転であるが、x-角度の$50$°の増加はこの回転において発生する。実際、図に示されるように今回のx軸周りの回転角度は $+(30° + 50°)$ となっている。つまり、第1の回転後の位置から 今回はx軸周りに$80$°の回転が行われるのである。
図26は第3の回転である y軸周りの回転が行われたときの様子である。第2の回転後の位置からy軸周りに$-70$°の回転が実行される。図26は、3つの回転すべてが実行されたときの状態でもあり、今回の場合は、図18の状態からx-角度を$50$°増加させた結果である図19の状態と同じ結果になっている。
オブジェクトに対してZ-X-Yオーダーのオイラー角による回転が行われ、そのときの x-角度、y-角度、z-角度が「x 30 y -70 z 20」であるとき、これらの数値が意味することは「オブジェクトに対し、z軸周りに$20$°、x軸周りに$30$°、y軸周りに$-70$°の順で回転を行った」ということである。
さらに x-角度を$50$°増加させ、3つの角度が「x 80 y -70 z 20」になったとき、これらの数値が意味することは、上の場合と同様に「オブジェクトに対し、z軸周りに$20$°、x軸周りに$80$°、y軸周りに$-70$°の順で回転を行った」ということである。
ある時点において x-角度、y-角度、z-角度がどのような数値であっても、また、それらをどのように変化させても、(Z-X-Yオーダーの)オイラー角による回転をオブジェクトに実行する場合は、オブジェクトに対し、z軸周りに#°、x軸周りに#°、y軸周りに#°の順で回転が行われるのである。
以下の図27は図26の状態と同じであり、ラベル表示を必要なものだけにしたものである。
最後に、この図27の状態からさらに z-角度を$80$°増加させた場合を見てみよう。図27では FinBallの状態は「x 80 y -70 z 20」であるが、これは FinBallが緯度$80$°、経度$-70$°の位置において$20$°のRoll回転を行っている状態であることを意味する。
図28は、図27の状態から z-角度を$80$°増加させたときの様子である。
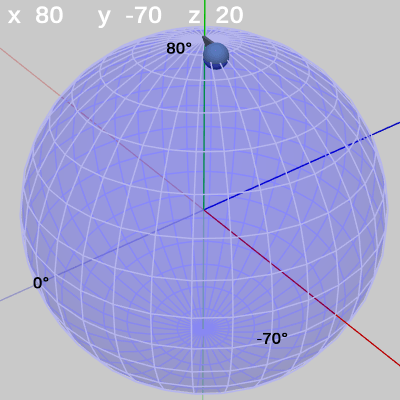
図27 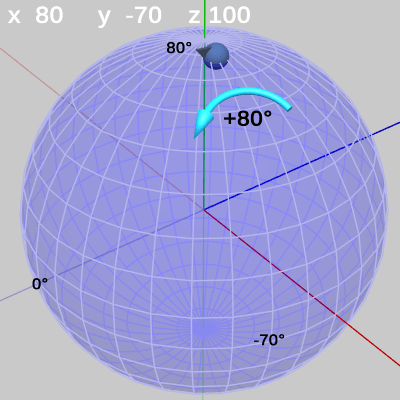
図28
z-角度を変化させると、FinBallがどこにいてもその位置においてRoll回転をすることになる。ここでは z-角度を$80$°増加させているが、これによって FinBallは現在いる地点(緯度$80$°、経度$-70$°)において$80$°のRoll回転を行うことになり、3つの角度は「x 80 y -70 z 100」という内容に変化する。
以下の図は、図28の状態(「x 80 y -70 z 100」)になるまでの過程である。

図21 
図29

図30 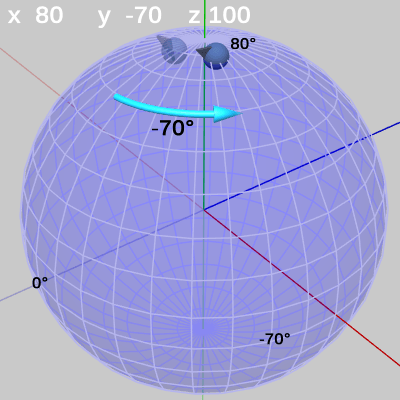
図31
図21は FinBallの初期状態である。図29は第1の回転である z軸周りの回転であるが、z-角度の$80$°の増加はこの回転において発生する。図に示されるようにここでのz軸周りの回転角度は $+(20° + 80°)$ となっている。今回は、FinBallは第1の回転である z軸周りの回転で$100$°の回転を行うのである。 図30は第2の回転である x軸周りの回転が行われたときの様子であり、第1の回転後の位置から x軸周りに$80$°の回転を行っている。図31は第3の回転である y軸周りの回転が行われたときの様子であり、第2の回転後の位置から y軸周りに$-70$°の回転を行っている。図31は3つの回転すべてが実行されたときの状態でもあり、図28の状態と同じである。
[Code1]
プログラム中で使われている i_eulX、i_eulY、i_eulZ は、それぞれ x-角度、y-角度、z-角度を表すインスタンス変数で、本節の図における白い数字はこれらの値を表したものである。14行目の TH3DMath.GetEulerRotation4x4() はカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。取得される回転行列 R は、z軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
このプログラムは、Xキー、Yキー、Zキーを押して i_eulX、i_eulY、i_eulZ の値を変化させるもので、1回押すごとに角度が$10$°ずつ増加する(長押しには対応していない)。また、Shiftキーと同時に押すと角度が$10$°ずつ減少する (プログラム中の THUtil.IsShiftDown() はShiftキーが押されていればtrueを返すカスタムライブラリのメソッドである)。
なお、このCode1及び次のCode2では x-角度の変更範囲は $-90$° から $90$° の範囲に制限してある。つまり、x-角度を押し続けても $90$° あるいは $-90$° を越える値にはならない。
プログラム実行中に各キーを押すことで、本節のアニメーションで見たように Finballが球面上において経線、緯線上を$10$°ずつ移動したり、あるいは$10$°ずつRoll回転を行うようになる。
[Code2]
このプログラムは、Code1において Input.GetKeyDown(..) となっていた箇所を Input.GetKey(..) に変え、1フレームあたりの角度の増減を $1$°ずつに変更しただけである。
今までに見てきた回転行列は、回転軸と角度を指定して得られるものであった。オイラー角によって回転行列を取得する場合には、次の3つの角度、すなわち x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度が必要になる。この3つの角度をもとにして回転行列を計算するわけであるが、このときに重要なのが回転の順序である。
オイラー角による回転は x軸周りの回転、y軸周りの回転、z軸周りの回転を合成したものである。例えば x軸周りに回転させ、次にy軸周りの回転、最後にz軸周りの回転の順で行うのか、あるいは、まず z軸周りに回転させ、次にy軸周りの回転、最後にx軸周りの回転の順で行うのかといったように回転の順序をあらかじめ決めておかなければならない。順序のパターンはいくつかあるが、どういった順序で回転を行うかは、使用しているゲームエンジンやDCCツールによって異なる。Unityの場合は、Z-X-Yの順序である。すなわち、まず z軸周りの回転、次にx軸周りの回転、最後にy軸周りの回転の順で行われる。
オイラー角による回転は3つの軸の周りの回転の合成なので、3つの変換行列の積で表される。
x軸周りの回転行列を $R_x$、y軸周りの回転行列を $R_y$、z軸周りの回転行列を $R_z$ とするときの Z-X-Yオーダーのオイラー角による回転行列 $R_{zxy}$ は
\[ R_{zxy} = R_yR_xR_z \]である。
行列の成分までを具体的に示せば(それぞれの軸における回転角度を $X$、$Y$、$Z$ とする)
\[R_x = \begin{pmatrix}1 &0 &0 \\0 &\cos X &-\sin X\\0 &\sin X &\cos X \end{pmatrix}\qquad R_y = \begin{pmatrix}\cos Y &0 &\sin Y\\0 &1 &0\\-\sin Y &0 &\cos Y\\\end{pmatrix}\qquad R_z = \begin{pmatrix}\cos Z &-\sin Z &0\\\sin Z &\cos Z &0\\0 &0 &1\end{pmatrix}\]
であるから、\begin{align*}R_{zxy} &= R_yR_xR_z \\\\&=\begin{pmatrix}\cos Y &0 &\sin Y\\0 &1 &0\\-\sin Y &0 &\cos Y\\\end{pmatrix}\begin{pmatrix}1 &0 &0 \\0 &\cos X &-\sin X\\0 &\sin X &\cos X \end{pmatrix}\begin{pmatrix}\cos Z &-\sin Z &0\\\sin Z &\cos Z &0\\0 &0 &1\end{pmatrix} \\\\&=\begin{pmatrix}\cos Y &0 &\sin Y\\0 &1 &0\\-\sin Y &0 &\cos Y\\\end{pmatrix}\begin{pmatrix}\cos Z &-\sin Z &0 \\\cos X\sin Z &\cos X\cos Z &-\sin X \\\sin X\sin Z &\sin X\cos Z &\cos X\end{pmatrix} \\\\&=\begin{pmatrix}\cos Y\cos Z + \sin X\sin Y\sin Z &-\cos Y\sin Z + \sin X\sin Y\cos Z &\cos X\sin Y \\\cos X\sin Z &\cos X\cos Z &-\sin X \\-\sin Y\cos Z + \sin X\cos Y\sin Z &\sin Y\sin Z + \sin X\cos Y\cos Z &\cos X\cos Y\end{pmatrix}\end{align*}
として求められる。プログラムで使用する場合には以下のように記述される (同次座標に対応させるため $4\times 4$ 行列として作成している)。
// オイラー角の順序は Z-X-Y
Matrix4x4 EulerRotation4x4(float eulX, float eulY, float eulZ)
{
float radX = eulX * Mathf.Deg2Rad;
float radY = eulY * Mathf.Deg2Rad;
float radZ = eulZ * Mathf.Deg2Rad;
float cosX = Mathf.Cos(radX), sinX = Mathf.Sin(radX);
float cosY = Mathf.Cos(radY), sinY = Mathf.Sin(radY);
float cosZ = Mathf.Cos(radZ), sinZ = Mathf.Sin(radZ);
Vector4 c1 = new Vector4
(cosY*cosZ + sinX*sinY*sinZ, cosX*sinZ, -sinY*cosZ + sinX*cosY*sinZ, 0.0f);
Vector4 c2 = new Vector4
(-cosY*sinZ + sinX*sinY*cosZ, cosX*cosZ, sinY*sinZ + sinX*cosY*cosZ, 0.0f);
Vector4 c3 = new Vector4
(cosX*sinY, -sinX, cosX*cosY, 0.0f);
Vector4 c4 = new Vector4(0, 0, 0, 1);
return new Matrix4x4(c1, c2, c3, c4);
}
上記の計算をそのまま実装したものである。引数の eulX、eulY、eulZ は各軸の回転角度であるが、これは度数法で表されているため Mathf.Sin(..) や Mathf.Cos(..) などの引数として使うためには弧度法による角度に変換しなければならない (4~6行目)。
では以下で、オイラー角を可視化した使用例を見ていく。この講義において用いられるオイラー角の回転順序は一部を除きすべてUnityと同じく Z-X-Yオーダーである。
なお細かいことではあるが1点追記する。オイラー角による回転には、回転軸を固定して考える回転と、回転軸をオブジェクトと一体化して考える回転の2つに分かれる。前者を extrinsic rotations、後者を intrinsic rotations という。Unityに用意されているQuaternion構造体のstaticメソッド Quaternion.Euler(x, y, z) は、オイラー角による回転を表すQuaternionを取得するメソッドであるが、このメソッドから返されるQuaternionを使用して確認する限りでは、Unityにおけるオイラー角回転は回転軸固定の extrinsic rotations である。したがって、この講義においてもオイラー角回転は extrinsic rotations によるものとして進めていく。ただし、オイラー角回転といえば intrinsic rotations を指すことが普通である (intrinsic rotations については次節を参照)。
より詳しくいえば、extrinsic rotations とはオブジェクトの親座標系のx軸、y軸、z軸を回転軸とする回転であり、intrinsic rotations とはオブジェクトのローカル座標系のx軸、y軸、z軸を回転軸とする回転である (オブジェクトの親座標系やローカル座標系については4-8節で解説する)。
A) 球面上での可視化
オイラー角による回転は、指定する3つの角度から回転がどのようなものであるかをイメージしやすいという優れた性質がある。まず、この性質から始めよう。

図1のオブジェクトFinBallは、初期状態で $(0,\ 0, -1)$に置かれている上部に突起のついた球である。図2は半径1の球面とFinBallをやや離れた位置から見たものである。球面の半径は $1$なので、初期状態のFinBallは図のように球面上の$(0,\ 0, -1)$にある。上の白い数字はそれぞれ x軸、y軸、z軸周りの回転角度であり、この3つの角度をもとにしてオイラー角による回転行列を計算し、それをFinBallに実行する。この数字はFinBallの初期状態ではすべて $0$であるが、これはFinBallに何も回転が実行されていないことを示している。

緯度、経度の起点(すなわち $0$°の位置)はFinBallの初期状態の位置である $(0,\ 0, -1)$とする。本節及び次節で使われる図においては、$0$° は常に緯度、経度ともに$0$°の位置であることを示している。
度数の増減は $(0,\ 0, -1)$を起点としてプラス、マイナスで表記する。以下は図3を参考に説明する。
緯度に関しては、経線上(縦方向の線)で起点より上側はプラスの値であり、上に進むにつれて増加する。経線上で起点より下側はマイナスの値であり、下に進むにつれて減少する(緯度$90$°、$-90$°は、地球でいえば北極点、南極点である)。また、ある経線上の緯度$180$°と$-180$°は同じ地点である。
経度に関しては、緯線上(横方向の線)で起点より左側はプラスの値であり、左に進むにつれて増加する。緯線上で起点より右側はマイナスの値であり、右に進むにつれて減少する。また、ある緯線上の経度$180$°と$-180$°は同じ地点である。
なお、x軸周りの回転角度、y軸周りの回転角度、z軸周りの回転角度については単に x-角度、y-角度、z-角度と表記する。
これらの用語を用いて、可視化されたオイラー角の回転について解説する。
本節のアニメーションは、次のコードにおけるオイラー角の数値を変えてFinBallに実行した結果である。
Matrix4x4 R_zxy = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ); FinBall.SetMatrix(R_zxy);
TH3DMath.GetEulerRotation4x4(..)はカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。i_eulX、i_eulY、i_eulZは、それぞれ x-角度、y-角度、z-角度を表すインスタンス変数で、図の白い数字はこれらの値を表したものである。取得される回転行列R_zxyは、上で述べたようにz軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
次の図4はx-角度だけを$10$°ずつ増減させたもの、図5はy-角度だけを$10$°ずつ増加させたもの、図6はz-角度だけを$10$°ずつ増減させたものである。
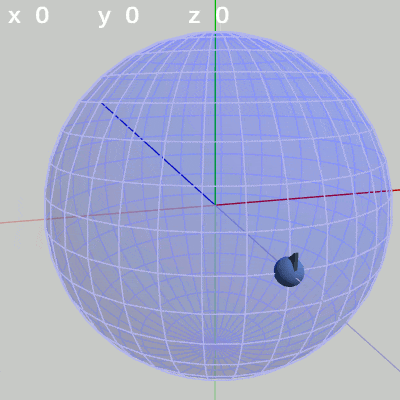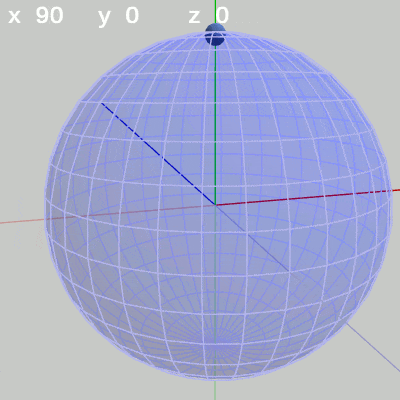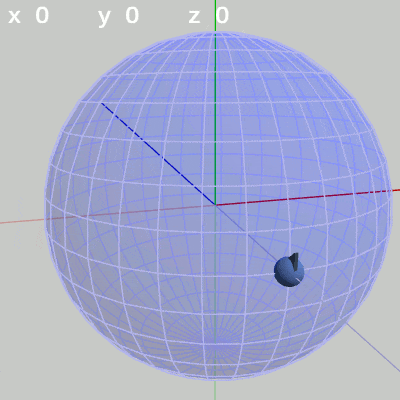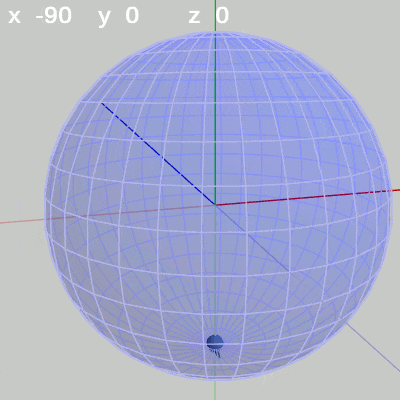 図4 x軸周りの回転角度のみを増減
図4 x軸周りの回転角度のみを増減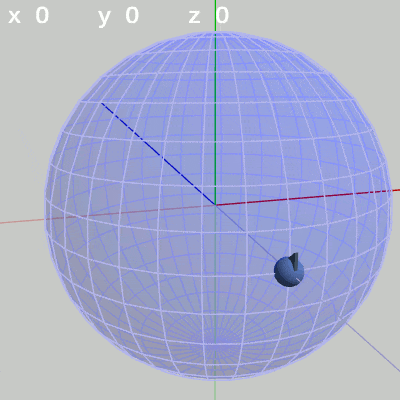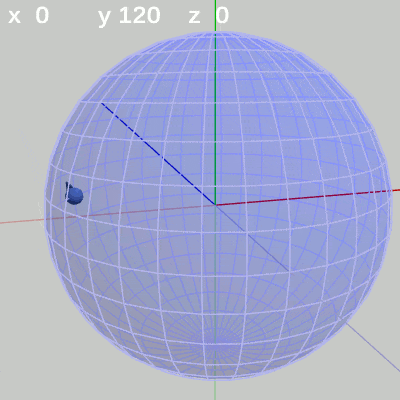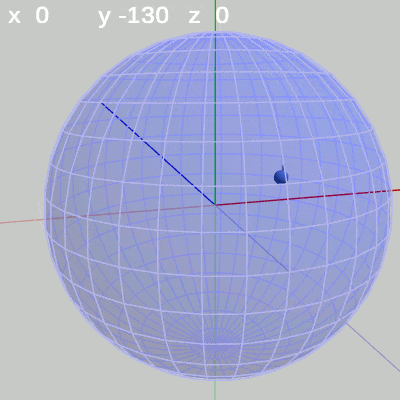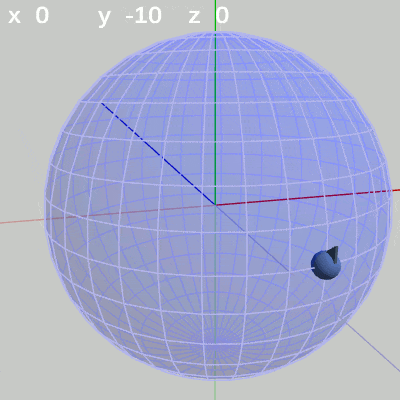 図5 y軸周りの回転角度のみを増加
図5 y軸周りの回転角度のみを増加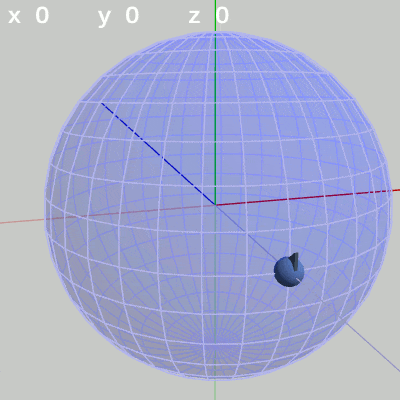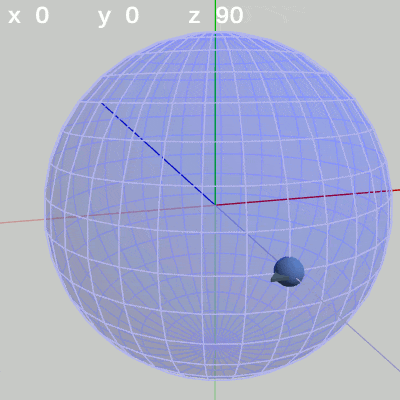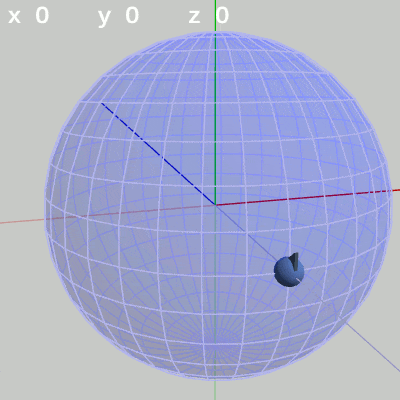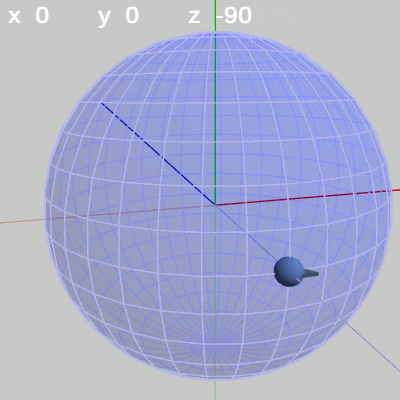 図6 z軸周りの回転角度のみを増減
図6 z軸周りの回転角度のみを増減
x-角度だけを変える場合、FinBallは縦方向の線、つまり経線上を動く(図4)。
y-角度だけを変える場合、FinBallは横方向の線、つまり緯線上を動く(図5)。
z-角度だけを変える場合は、FinBallの球面上での位置の変化は起こらない。この場合のFinBallはその場所において図6に示される回転を行うが、本節及び次節では図6のような回転を「Roll回転」と呼ぶことにする。
次の図は、y-角度を左から $y = 50$°、$y = 140$°、$y = -20$°に固定して、x-角度だけを変化させたものである。
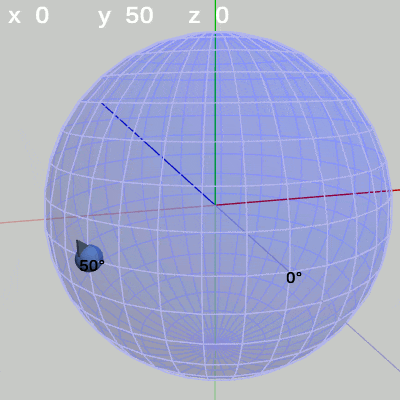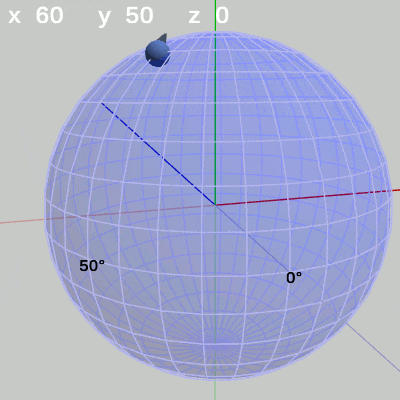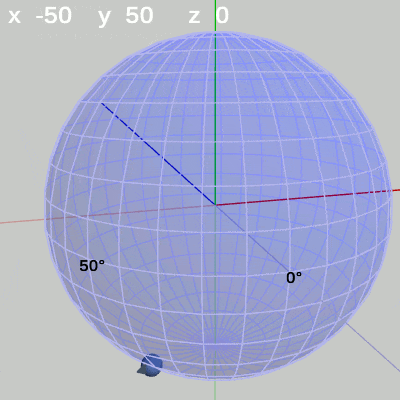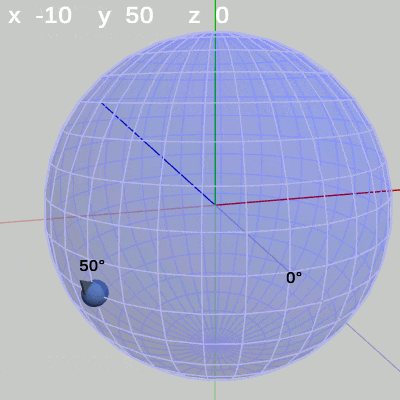 図7 x-角度の変化 (y = 50°)
図7 x-角度の変化 (y = 50°)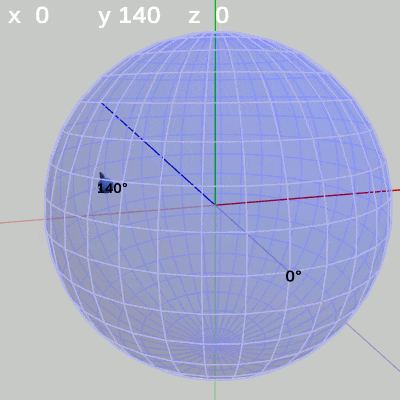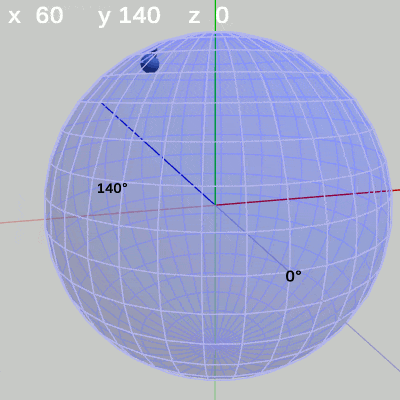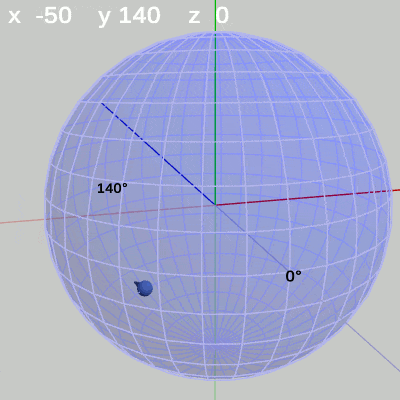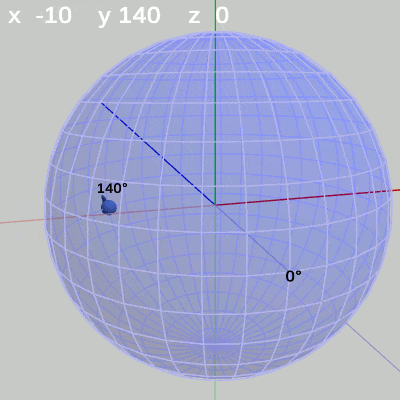 図8 x-角度の変化 (y = 140°)
図8 x-角度の変化 (y = 140°)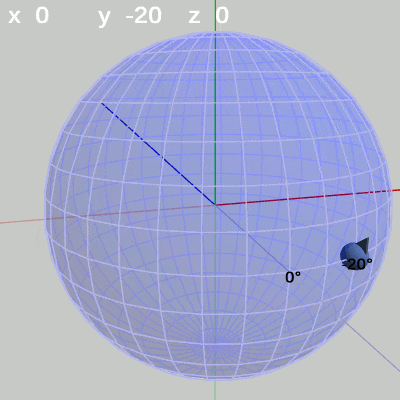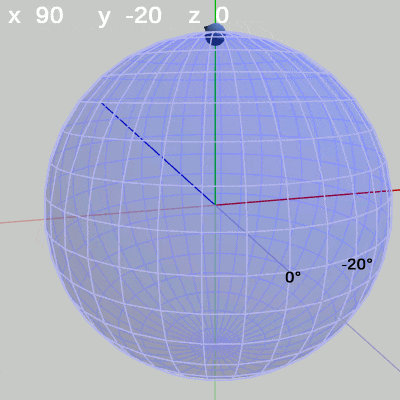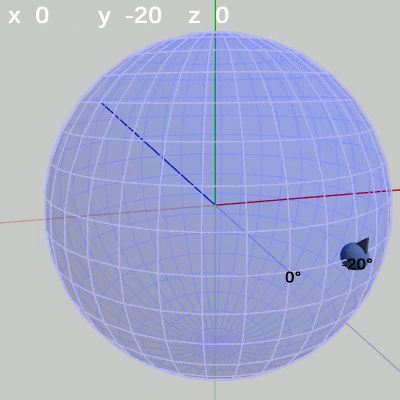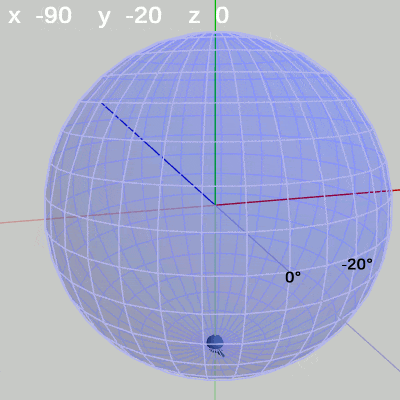 図9 x-角度の変化 (y = -20°)
図9 x-角度の変化 (y = -20°)
y-角度を$50$°に固定して、x-角度だけを変化させる場合は、経度$50$°の経線上を動く(図7)。
y-角度を$140$°に固定して、x-角度だけを変化させる場合は、経度$140$°の経線上を動く(図8 ; 経度$140$°は球面の裏側の経線)。
y-角度を$-20$°に固定して、x-角度だけを変化させる場合は、経度$-20$°の経線上を動く(図9)。
次の図は、x-角度を左から $x = -30$°、$x = 20$°、$x = 60$°に固定して、y-角度だけを変化させたものである。
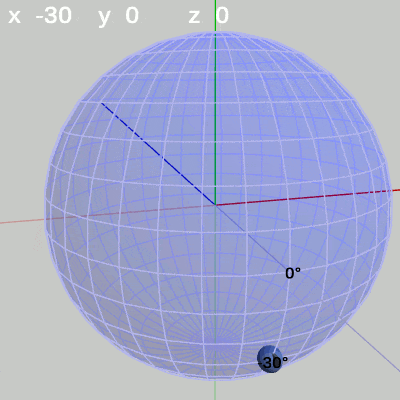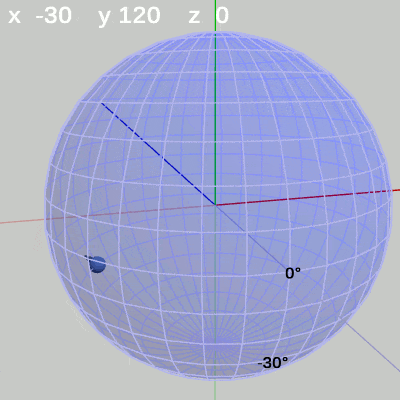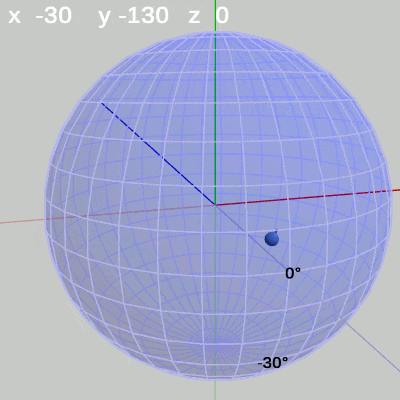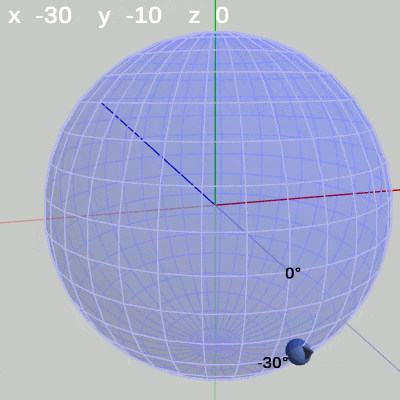 図10 y-角度の変化 (x = -30°)
図10 y-角度の変化 (x = -30°)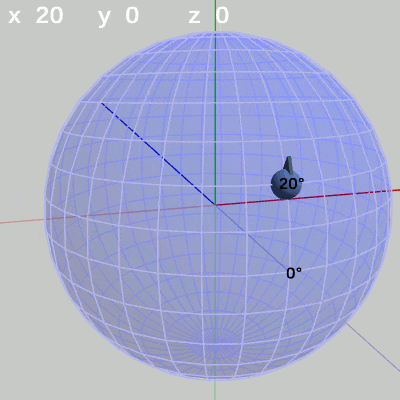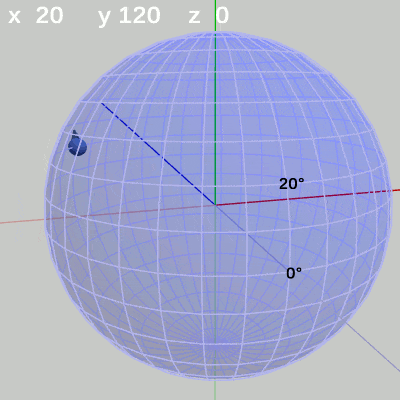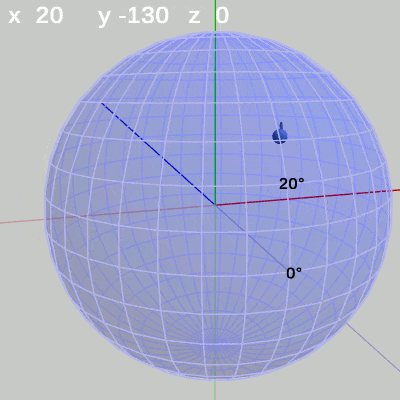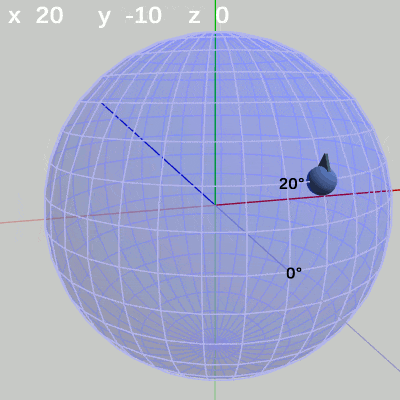 図11 y-角度の変化 (x = 20°)
図11 y-角度の変化 (x = 20°)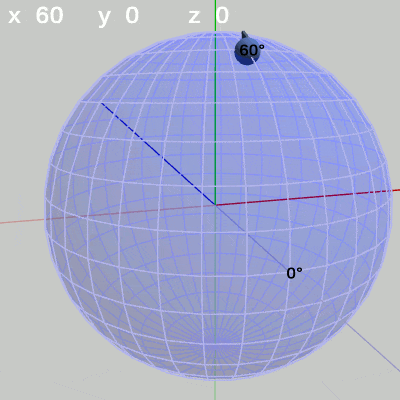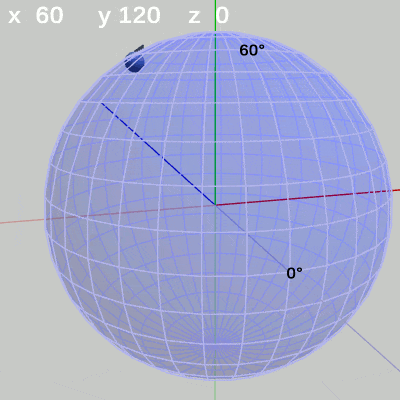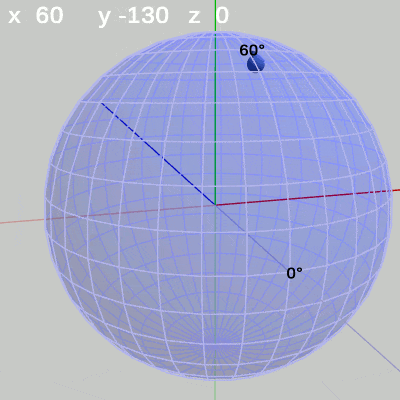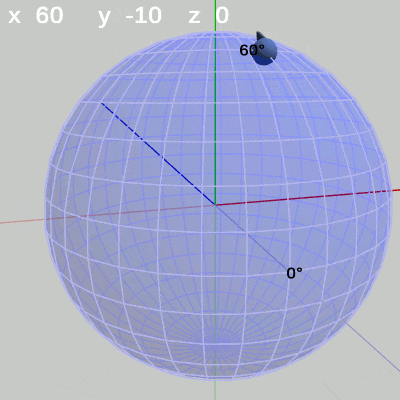 図12 y-角度の変化 (x = 60°)
図12 y-角度の変化 (x = 60°)
x-角度を$-30$°に固定して、y-角度だけを変化させる場合は、緯度$-30$°の緯線上を動く(図10)。
x-角度を$20$°に固定して、y-角度だけを変化させる場合は、緯度$20$°の緯線上を動く(図11)。
x-角度を$60$°に固定して、y-角度だけを変化させる場合は、緯度$60$°の緯線上を動く(図12)。
次の図は、x-角度、y-角度を左から $(x = 20^\circ,\ y = 40^\circ)$、$(x = 10^\circ,\ y = 10^\circ)$、$(x = 30^\circ,\ y = -140^\circ)$に固定して、z-角度だけを変化させたものである (図13に表示されているFinBallから原点へ向けられている青い矢印は この回転の回転軸である)。
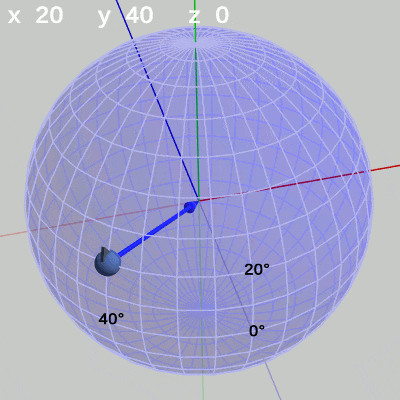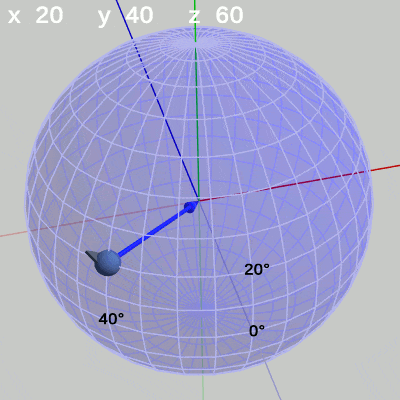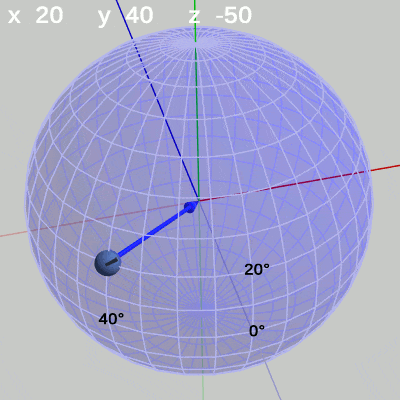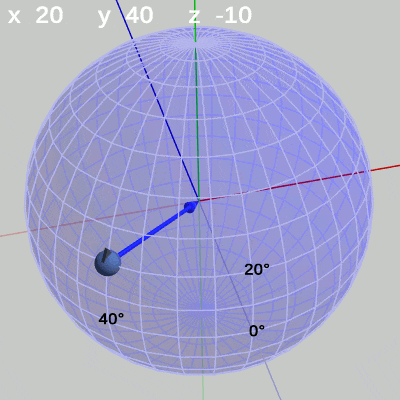 図13 z-角度の変化 (緯度 20°, 経度 40°)
図13 z-角度の変化 (緯度 20°, 経度 40°)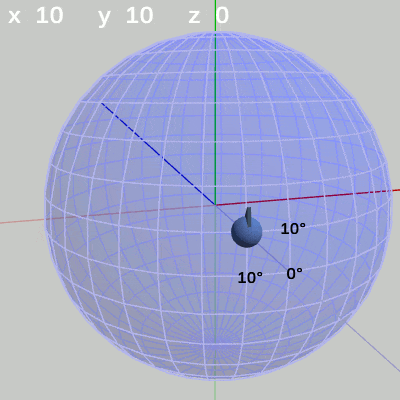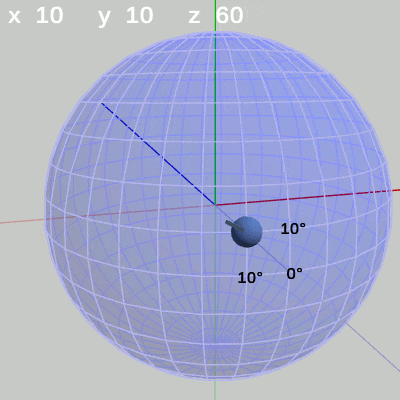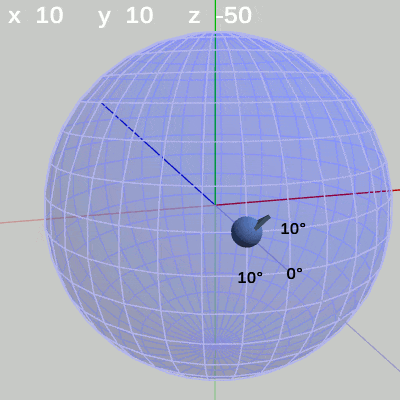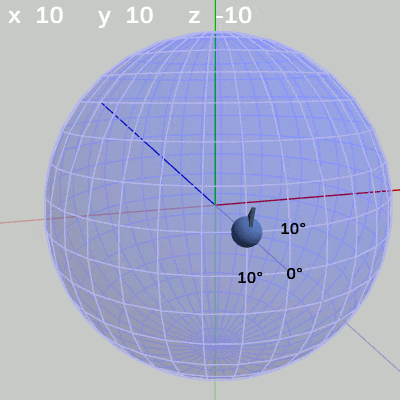 図14 z-角度の変化 (緯度 10°, 経度 10°)
図14 z-角度の変化 (緯度 10°, 経度 10°)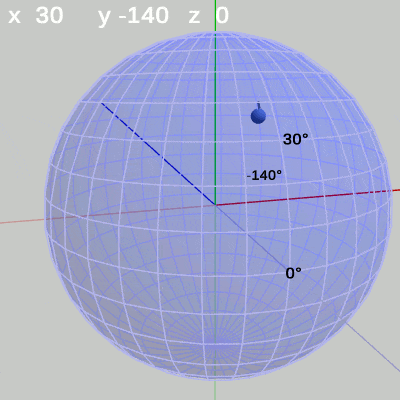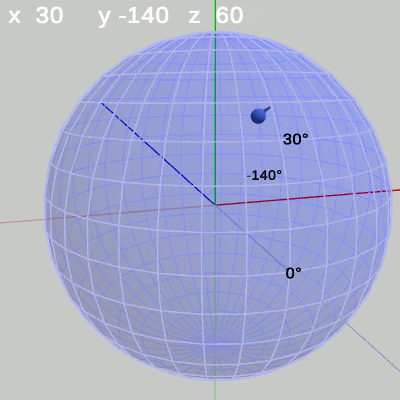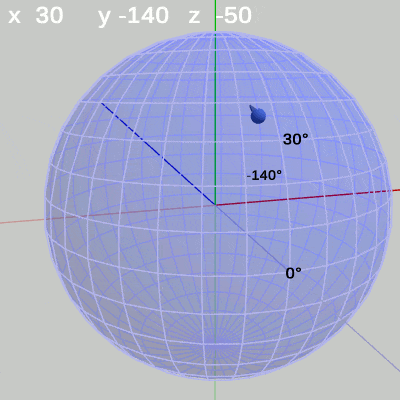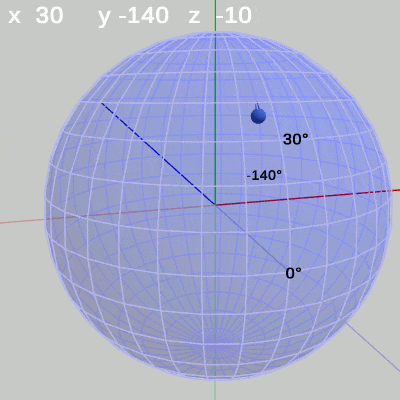 図15 z-角度の変化 (緯度 30°, 経度 -140°)
図15 z-角度の変化 (緯度 30°, 経度 -140°)
z-角度だけを変化させる場合は、球面上のどの地点においても、その場所でRoll回転をするのである。たとえば、図13の場合は x-角度 $20$°、y-角度 $40$° であるが、このときにz-角度を変化させると球面上の緯度$20$°、経度$40$°の位置でRoll回転を行うことになる。Roll回転とは、FinBallの場合では図13に示されるように原点と球の中心を結ぶ軸周りの回転となる (オブジェクトの初期状態でオブジェクトの中に原点が含まれる場合は、Roll回転は原点を通りオブジェクトを貫通する軸周りの回転となる。「オブジェクトを貫通する軸」は状況によって変化するが、Z-X-Yオーダーにおいてx-角度、y-角度を変化させていない $0$°のままの状態では、Roll回転はz軸周りの回転と同じである。具体例については次節参照)。
以上をまとめると、オブジェクトが初期状態でz軸上(の原点以外の位置)に置かれている場合、Z-X-Yオーダーのオイラー角による回転行列をオブジェクトに実行すると、オブジェクトから原点までの距離を半径とする球面上を オブジェクトは運動することになる。
具体的には、x-角度を変化させるとオブジェクトがどこにいても、その位置から縦方向、すなわち経線上を動き、y-角度を変化させるとオブジェクトがどこにいても、その位置から横方向、すなわち緯線上を動く。z-角度を変化させる場合はオブジェクトがどこにいても、その位置でRoll回転を行う。
ここで使用している FinBallの場合でいえば、x-角度、y-角度、z-角度が「x 60 y 120 z -30」であるとき、FinBallは単位球面上において 緯度$60$°、経度$120$°の位置にあり、その位置において$-30$°のRoll回転がなされていることを意味する。
このように、オイラー角による回転は指定された3つの角度から結果をイメージしやすいのである。
オブジェクトが初期状態で、図16のように原点に置かれている場合でも、上記のような球面上でオブジェクトを運動させることは、オイラー角を用いることによって簡単に実現できる。


図16のオブジェクトSphereの初期状態での位置は原点であるが、仮に初期状態での位置が$(0, \ 0, -8)$であったとしよう。その場合は、Sphereに対してオイラー角による回転行列を実行すると、上で述べたように$(0, \ 0, -8)$から原点までの距離を半径とする球面、すなわち半径$8$の球面上をSphereは運動することになる。この場合の球面上でのSphereの位置は、Sphereに実行したものとおなじ回転行列を$(0, \ 0, -8)$に掛ければ求められる。
結局、Sphereが初期状態で原点にある場合でも、半径$r$ の球面上の緯度$a$、経度$b$の地点に移動させるためには、オイラー角のx-角度、y-角度を $a$、$b$とした回転行列を求めて、それを$(0, \ 0, -r)$に掛けて球面上の緯度$a$、経度$b$の地点の座標値を算出し、その座標の位置にSphereを移動させればよい。コードで表すと次のようになる。
初期状態で原点に置かれているSphereを半径$r$ の球面上の緯度$a$、経度$b$の位置に移動させる処理(ただし緯度、経度の起点は $(0, \ 0, -r)$ とする ; また、以下のコードから分かるように Shepreは球面上の指定された緯度、経度の位置へ移動するが、Spehreの向きは初期状態から変わらない。Spehreに実行される変換は平行移動だけである)。
Vector4 pos0 = new Vector4(0.0f, 0.0f, -r, 1.0f); // 同次座標 Matrix4x4 R_zxy = TH3DMath.GetEulerRotation4x4(a, b, 0); Vector3 wp = R_zxy * pos0; Sphere.SetLocalPosition(wp);
4行目の SetLocalPosition(Vector3 v) は、引数に指定されたベクトル分移動させるカスタムライブラリーのメソッドである。2行目で計算されるオイラー角による回転行列は$4\times4$行列なので$(0, \ 0, -r)$を表すpos0も同次座標になっている。3行目では$4\times4$行列と4次元ベクトルの積の結果をVector3型にセットしているが、これは左辺をVector3型にすることによってUnityでは、$4\times4$行列と4Dベクトルの積のw座標が自動的に取り除かれてセットされるのである。
例えば図16のオブジェクトSphererを半径$8$の球面上の緯度$40$°の緯線上で、経度$-30$°から$60$°まで毎フレーム$10$°ずつ移動させるプログラムは以下のようになる(実行結果 図17 ; 3行目のi_eulYのここでの初期値は$-30$)。
Vector4 pos0 = new Vector4(0.0f, 0.0f, -8.0f, 1.0f); // 同次座標 i_eulY += 10; // -30 から 60 まで Matrix4x4 R_zxy = TH3DMath.GetEulerRotation4x4(40, i_eulY, 0); Vector3 wp = R_zxy * pos0; Sphere.SetLocalPosition(wp);
今まで見てきたとおり、z軸上のある地点を起点とすれば、その起点から原点までの距離を半径とする球面において、オイラー角のx-角度、y-角度は、球面上の緯度、経度にそのまま対応している。x-角度、y-角度の数値を見れば、オブジェクトが球面上のどの位置にいるかを容易にイメージすることができる。これがオイラー角の球面上における可視化である。
B) 補足
上記ではオイラー角指定の回転による、FinBallの単位球面上での運動を見てきた。例えば、x-角度を変化させるとどういった状況においても FinBallはそのときいる場所から経線上を動く。また、z-角度を変化させると FinBallはそのときいる場所において Roll回転を行う。ここからは、FinBallがなぜその状況でそういった運動をするのかということについての補足的な解説をする。FinBallがオイラー角による回転によって図18に示される状態になったとする (初期状態での位置は図2と同じ $z=-1$ である)。
-
 図18
図18 -
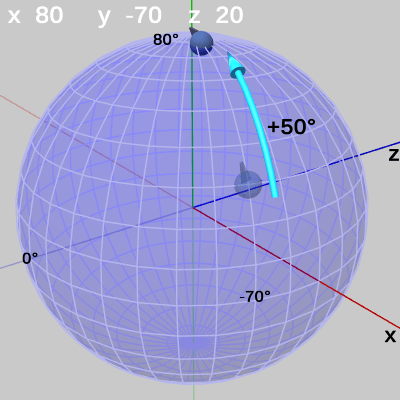 図19
図19 -
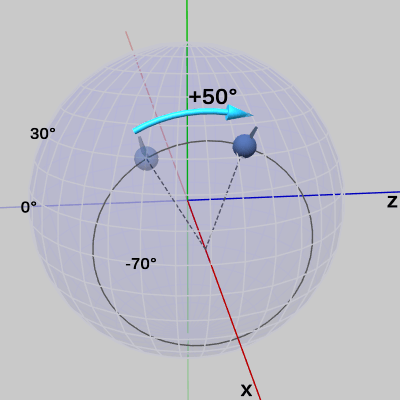 図20
図20
図18に示されるように、この状態においての x-角度、y-角度、z-角度はそれぞれ $30$°、$-70$°、$20$°である (すなわち 緯度$30$° 経度$-70$° の位置にあり、$20$°のRoll回転がなされている)。今 この状態からオイラー角の x-角度を$50$°増加させるとしよう。上で述べてきたように、x-角度の増減によって FinBallは経線上を動くことになる。したがって、このときに FinBallに起こる変換は図18の位置から経線上を$50$°分動くことになる。図19は x-角度を$50$°増加させたときの様子である。
Z-X-Yオーダーのオイラー角による回転の場合は、x-角度を変化させることと x軸周りに回転を行うことは必ずしも同じではない (同じである場合もある)。例えば、図20は 図18の状態から FinBallを x軸周りに$50$°回転させたときの様子であるが、この結果は明らかに、図18の状態から x-角度を$50$°増加させた結果である図19とは異なる結果となっている。同様のことは z-角度についてもいえる。すなわち、Z-X-Yオーダーのオイラー角による回転の場合は、z-角度を変化させることと z軸周りに回転を行うことは必ずしも同じではない (同じである場合もある)。しかし、Z-X-Yオーダーの場合は y-角度を変化させることと y軸周りの回転は同じ結果になる (つまり、y-角度を変化させると常にy軸周りの回転になる)。
x-角度を$50$°増加させると、その時にいる位置から経線上を$50$°分動いた位置に移る結果になったが、以下ではこの変換過程を順を追って見ていこう。まずは、x-角度を$50$°増加させる前の状態 「x 30 y -70 z 20」 になる過程から始める。




図21は FinBallの初期状態であり $z = -1$ に位置している。図22は Z-X-Yオーダーの最初の回転である、z軸周りの回転が行われたときの様子である。ここではz軸周りに$20$°の回転である。図23は第2の回転である x軸周りの回転が行われたときの様子であり、第1の回転後の位置からx軸周りに$30$°の回転が行われている。図24は第3の回転である y軸周りの回転が行われたときの様子である。第2の回転後の位置からy軸周りに$-70$°の回転が実行される。図24は、この3つの回転すべてが実行されたときの状態でもあり、先程の図18の状態と同じものである。
Z-X-Yオーダーのオイラー角による回転で、それぞれの角度が「x 30 y -70 z 20」という値であることは、オブジェクトに対して 今述べた3つの回転が指定の順序で実行されていることを意味している。
では次に、この状態から x-角度を$50$°増加させる。このとき、それぞれの角度は「x 80 y -70 z 20」となり、FinBallは図19に示される状態になるが、これもまた Z-X-Yオーダーの回転の結果なのである。以下の図はこの状態に至るまでの変換過程である。




図21、図22は先程と同様にそれぞれ FinBallの初期状態、及び z軸周りの$20$°の回転である。
図25は第2の回転である x軸周りの回転であるが、x-角度の$50$°の増加はこの回転において発生する。実際、図に示されるように今回のx軸周りの回転角度は $+(30° + 50°)$ となっている。つまり、第1の回転後の位置から 今回はx軸周りに$80$°の回転が行われるのである。
図26は第3の回転である y軸周りの回転が行われたときの様子である。第2の回転後の位置からy軸周りに$-70$°の回転が実行される。図26は、3つの回転すべてが実行されたときの状態でもあり、今回の場合は、図18の状態からx-角度を$50$°増加させた結果である図19の状態と同じ結果になっている。
オブジェクトに対してZ-X-Yオーダーのオイラー角による回転が行われ、そのときの x-角度、y-角度、z-角度が「x 30 y -70 z 20」であるとき、これらの数値が意味することは「オブジェクトに対し、z軸周りに$20$°、x軸周りに$30$°、y軸周りに$-70$°の順で回転を行った」ということである。
さらに x-角度を$50$°増加させ、3つの角度が「x 80 y -70 z 20」になったとき、これらの数値が意味することは、上の場合と同様に「オブジェクトに対し、z軸周りに$20$°、x軸周りに$80$°、y軸周りに$-70$°の順で回転を行った」ということである。
ある時点において x-角度、y-角度、z-角度がどのような数値であっても、また、それらをどのように変化させても、(Z-X-Yオーダーの)オイラー角による回転をオブジェクトに実行する場合は、オブジェクトに対し、z軸周りに#°、x軸周りに#°、y軸周りに#°の順で回転が行われるのである。
以下の図27は図26の状態と同じであり、ラベル表示を必要なものだけにしたものである。
最後に、この図27の状態からさらに z-角度を$80$°増加させた場合を見てみよう。図27では FinBallの状態は「x 80 y -70 z 20」であるが、これは FinBallが緯度$80$°、経度$-70$°の位置において$20$°のRoll回転を行っている状態であることを意味する。
図28は、図27の状態から z-角度を$80$°増加させたときの様子である。


z-角度を変化させると、FinBallがどこにいてもその位置においてRoll回転をすることになる。ここでは z-角度を$80$°増加させているが、これによって FinBallは現在いる地点(緯度$80$°、経度$-70$°)において$80$°のRoll回転を行うことになり、3つの角度は「x 80 y -70 z 100」という内容に変化する。
以下の図は、図28の状態(「x 80 y -70 z 100」)になるまでの過程である。




図21は FinBallの初期状態である。図29は第1の回転である z軸周りの回転であるが、z-角度の$80$°の増加はこの回転において発生する。図に示されるようにここでのz軸周りの回転角度は $+(20° + 80°)$ となっている。今回は、FinBallは第1の回転である z軸周りの回転で$100$°の回転を行うのである。 図30は第2の回転である x軸周りの回転が行われたときの様子であり、第1の回転後の位置から x軸周りに$80$°の回転を行っている。図31は第3の回転である y軸周りの回転が行われたときの様子であり、第2の回転後の位置から y軸周りに$-70$°の回転を行っている。図31は3つの回転すべてが実行されたときの状態でもあり、図28の状態と同じである。
# Code1
本節ではオブジェクトFinBallを用いてオイラー角についての解説をしたが、本節のアニメーションで見られるFinBallの運動は次のプログラムを実行したものである。[Code1]
if (Input.GetKeyDown(KeyCode.X))
{
i_eulX += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -10 : 10;
}
else if (Input.GetKeyDown(KeyCode.Z))
{
i_eulZ += (THUtil.IsShiftDown()) ? -10 : 10;
}
Matrix4x4 R = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ);
FinBall.SetMatrix(R);
プログラム中で使われている i_eulX、i_eulY、i_eulZ は、それぞれ x-角度、y-角度、z-角度を表すインスタンス変数で、本節の図における白い数字はこれらの値を表したものである。14行目の TH3DMath.GetEulerRotation4x4() はカスタムライブラリーのメソッドで、引数で指定された3つの角度を元にして、オイラー角による$4\times4$の回転行列を計算するものである。取得される回転行列 R は、z軸周りの回転、x軸周りの回転、y軸周りの回転をこの順序で行う行列である。
このプログラムは、Xキー、Yキー、Zキーを押して i_eulX、i_eulY、i_eulZ の値を変化させるもので、1回押すごとに角度が$10$°ずつ増加する(長押しには対応していない)。また、Shiftキーと同時に押すと角度が$10$°ずつ減少する (プログラム中の THUtil.IsShiftDown() はShiftキーが押されていればtrueを返すカスタムライブラリのメソッドである)。
なお、このCode1及び次のCode2では x-角度の変更範囲は $-90$° から $90$° の範囲に制限してある。つまり、x-角度を押し続けても $90$° あるいは $-90$° を越える値にはならない。
プログラム実行中に各キーを押すことで、本節のアニメーションで見たように Finballが球面上において経線、緯線上を$10$°ずつ移動したり、あるいは$10$°ずつRoll回転を行うようになる。
# Code2
Code1では、FinBallの運動はキーを1回1回押さなければいけないものあったが、次のプログラムはキー操作をキーの長押しに変更し、FinBallの運動が球面上においてなめらかに行われるようにしたものである。[Code2]
if (Input.GetKey(KeyCode.X))
{
i_eulX += (THUtil.IsShiftDown()) ? -1 : 1;
}
else if (Input.GetKey(KeyCode.Y))
{
i_eulY += (THUtil.IsShiftDown()) ? -1 : 1;
}
else if (Input.GetKey(KeyCode.Z))
{
i_eulZ += (THUtil.IsShiftDown()) ? -1 : 1;
}
Matrix4x4 R = TH3DMath.GetEulerRotation4x4(i_eulX, i_eulY, i_eulZ);
FinBall.SetMatrix(R);
このプログラムは、Code1において Input.GetKeyDown(..) となっていた箇所を Input.GetKey(..) に変え、1フレームあたりの角度の増減を $1$°ずつに変更しただけである。
© 2020-2025 Redpoll's 60 (All rights reserved)