Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-11
第3章 3D空間の基礎
$§$3-11 回転行列 2
前節ではx軸、y軸、z軸を回転軸とする回転行列を扱った。3D空間における回転で指定できる回転軸は、この3軸だけではなく無数に存在する。本節では、いわゆる行列による任意軸回転について見ていく。
単位ベクトルで表された回転軸 $\boldsymbol{n} = (n_x, n_y, n_z)$ の周りに角度 $\theta$ だけ回転させる行列($3\times 3$行列)
同次座標に対応させるために$4\times4$行列で表した場合
次のプログラムは前節でも使用した、カスタムライブラリーの回転行列を取得するメソッド TH3DMath.GetRotation4x4(float deg, Vector3 axis) である。このメソッドは上記の行列をそのまま実装しているので任意軸回転にも対応している。
[GetRotation4x4]
注意すべき点は、Unityでは行列を作成する際には引数に列をセットしなければならない。この場合では22行目の new Matrix4x4(c1, c2, c3, c4) の4つの引数には、それぞれ第1列目から第4列目を表すVector4データが渡されているのである。c1、c2、c3、c4は行列の各列を表すデータである(行ではない)。
なお、このメソッドの第2引数axisには回転軸を表すベクトルをセットするが、これは単位ベクトルでなくても構わない。このメソッドの冒頭で正規化されるからである。
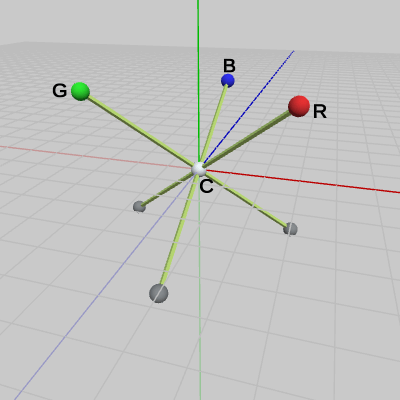
図1 Trino 初期状態
また、各腕の長さはみな等しく、各腕は互いに直交している。
では、このオブジェクトTrinoに任意軸周りの回転行列を実行していこう。
まず始めに、CからRの方向を回転軸として、この軸の周りに$50$°の回転を行う。図2における淡い赤色のベクトルは、この回転軸を表している(オブジェクトと重なっているため見えないが、このベクトルは原点を始点としている)。
Trinoの中心Cから出ている各腕の長さは等しく、互いに直交している。したがって、腕CG、CBは腕CRと直交している。さらに、長さについては CG = CB である。前節で述べたように、ある点を回転軸の周りに回転させることは、その点から回転軸へ垂線を下ろしたときの、垂線の足を中心とし、垂線の長さを半径とする円周上の回転に等しくなる。球G、Bを点とみれば、今回の場合は腕CG、CBは腕CRと直交しているので、それらの腕は点G、Bから回転軸へ下ろされた垂線とみなすことができる(球Cを点と考えれば、垂線の足が点Cである)。そしてCG、CBは長さが等しいので点G、Bが回転する円周は全く同じものになる(図3)。
オブジェクトTrinoに、上記の回転を実行するプログラムを以下に示す。
posR は球Rの(中心の)位置を表している。2行目の回転行列を取得するメソッドの第2引数には、回転軸を表すベクトルをセットするが、ここではposRが使われている。回転軸を表すベクトルは球Cから球Rの方向を表すベクトルなので、球Cの(中心の)位置を Center とすれば、CからRの方向は (posR - Center) である。Center は上で述べたように原点なので結局、(posR - Center) = posR となり、posRが回転軸を表すベクトルとして使われているのである。
このプログラムの実行結果は図4に示されている。
では次に、上記の回転をした状態のTrinoに対して、今度はCからGの方向を回転軸として、この軸の周りの回転を実行しよう(図5)。ここで注意すべきことは最初の回転でGの位置は動いているため、まず、Gの回転後の位置を求める必要がある。
ただし、これは次のように簡単に求めることができる。
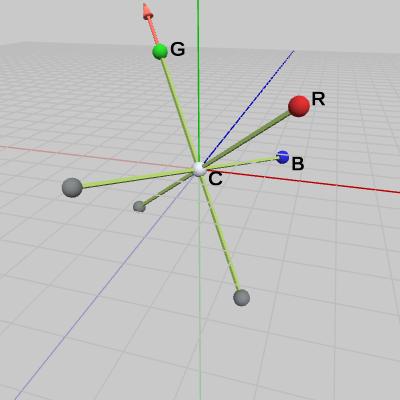
図5 C--G方向を表す回転軸(最初の回転後の状態 ; この状態でのGの位置が posG1) 2行目の posG は球Gの(中心の)位置を表している(この位置は回転前の位置、すなわち初期状態での位置である)。このposGに対しても同じように先ほどの回転行列を実行すれば、回転後の位置が得られるわけである。回転後のGの位置は、4行目で posG1 にセットされている。
したがって回転後のCからGの方向とは、上記の Center を再び使えば (posG1 - Center)、すなわち posG1 である。このposG1が、次の回転における回転軸を表すベクトルとして使われることになる(posG1は図5におけるGの位置を表す)。
以下では便宜上、最初の回転における回転軸をCR軸、第2の回転における回転軸をCG軸と表記する。
今回のプログラムは最初の回転後の状態から、CG軸周りに毎フレーム1°ずつ回転し続けるプログラムである(プログラム中のインスタンス変数i_degRotは回転角度を表し、毎フレーム$1$ずつ増加する)。
4行目までの処理は上で述べた通りである。最初の回転後の状態におけるCG軸を表すベクトルがposG1であり、7行目で回転行列を取得する際の回転軸を表す引数として、posG1をセットすることでCG軸周りの回転行列rotCGが得られる。ただし、このrotCGをそのままTrinoにセットしても意味がない。
今回実装する回転は、最初の回転後の状態から、CG軸周りに回転させなければならない。具体的には、図5の状態からCG軸周りに回転させることが必要なのである。もし、Trinoに行列をセットする際に上記の10~11行目を次のように書き換えて、
とした場合は図5の状態ではなく、図1の状態のTrinoに回転を実行してしまうことになる。そして、その場合の回転は図1におけるCG軸周りの回転にはならない。
7行目で取得した回転行列rotCGは、図5におけるTrinoのCG軸周りの回転であるので、毎フレーム、Trinoをまず図5の状態にしてからrotCGを実行しなければ意味がないのである。「図5の状態にする」とは、最初の回転であるCR軸周りの$50$°の回転を実行することである。これはプログラムの3行目で取得される回転行列rotCRを実行すればよい。
つまり、最初の回転後の状態からCG軸周りに回転させるためには、毎フレームTrinoにrotCRを実行し、その後にrotCGを実行しなければならない。10~11行目の処理がそれにあたるわけである。
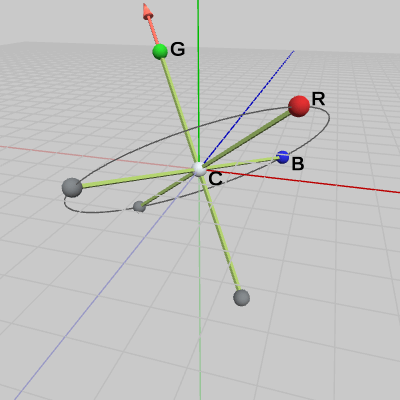
図6 RやBが回転する円周 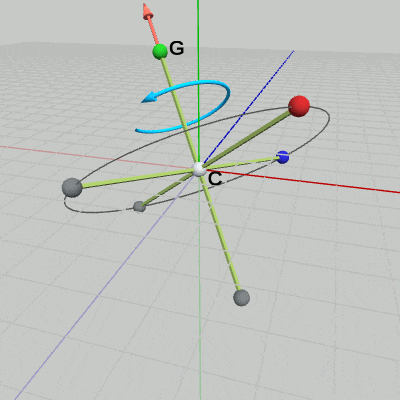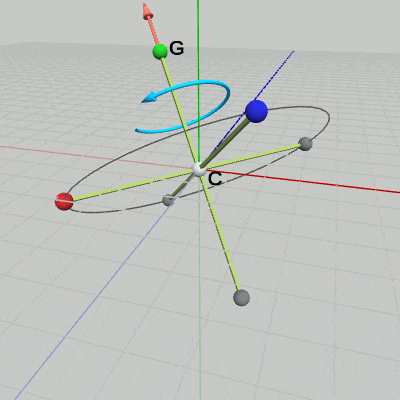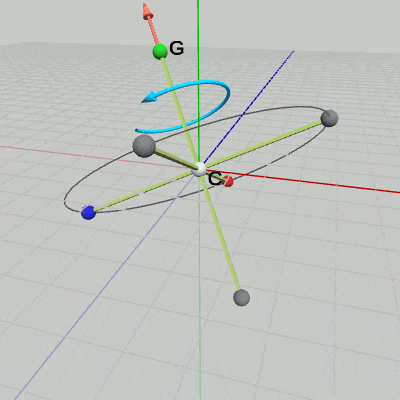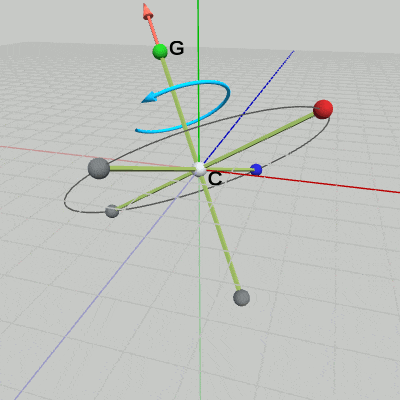
図7 CG軸周りの回転
今回の回転軸である腕CGと腕CR、CBは直交しており、長さについては CR = CB である。最初の回転の箇所でも説明したが、この場合にはR、Bの回転軌道は同じものになる(図6)。
図7は、CG軸周りの回転プログラムの実行結果である。
行列 $A$ が次の関係を満たすとき、$A$を直交行列という (以下の $A^T$ は $A$ の転置行列で、$I$ は単位行列(identity行列))。
\[A^TA = AA^T = I \]これは、直交行列 $A$ の転置行列 $A^T$ は $A$ の逆行列であることを意味する。すなわち、
\[A^T = A^{-1}\]である(逆行列については3-7節、転置行列については3-8節参照)。
先に述べた通り、回転行列も直交行列の一種であるから回転行列もこの性質を持っている。つまり、回転行列の逆行列を求めるには、その回転行列を転置すればよいのである。
(例)
y軸周りに角 $\theta$ 回転させる行列 $R_y$ とその転置行列である $R_y^T$ の積を計算してみよう。
$R_y$ の転置行列 $R_y^T$ が、確かに $R_y$ の逆行列になっている。これは、積の順序を入れ替えても同じ結果になる。また、同次座標用の $4\times4$ 行列で計算した場合の結果は、もちろん $4\times4$ の 単位行列(identity行列)である。
詳しい証明は省くが上の定義から、直交行列の各列について次の性質が導かれる。
たとえば、次の行列 $M$ が直交行列であるとしよう。\[ M = \begin{pmatrix}m_{11} &m_{12} &m_{13} &m_{14}\\m_{21} &m_{22} &m_{23} &m_{24}\\m_{31} &m_{32} &m_{33} &m_{34}\\m_{41} &m_{42} &m_{43} &m_{44}\end{pmatrix}\] $M$ はすべての列の大きさが $1$ であり、任意の2つの列は互いに直交しているので、第1列目 $(m_{11}, m_{21}, m_{31}, m_{41})$ と第2列目 $(m_{12}, m_{22}, m_{32}, m_{42})$ の内積や、第2列目 $(m_{12}, m_{22}, m_{32}, m_{42})$ と第4列目 $(m_{14}, m_{24}, m_{34}, m_{44})$ の内積はいずれも $0$ になるということである (このことは各列だけでなく各行についても成り立つ ; 詳しくは この性質を正規直交という)。
回転行列も直交行列に属すので、回転行列についても各列の大きさが $1$ であり、各列は互いに直交するという性質は満たされる。
回転行列は直交行列ではあるが、直交行列がすべて回転行列であるかというと、そうではない。具体的には、回転行列の場合は、
という2つの性質の他に、もう1つ次の性質が満たされていることが必要である。
つまり回転行列はこの3つの性質が満たされていなければならないのである (この3つの性質のうち1つでも欠けると回転行列にはならない ; ここに現れた「行列式」についての解説は数学的にやや深入りすることになるので省略するが、回転行列の場合における行列式が $1$ であるという性質が何を意味するかについては以下の解説を参照)。
ここではこの3つの性質から回転行列を目に見える形で表してみよう。
結論から先にいえば回転行列を可視化したものは大きさが $1$ の座標系、具体的には大きさが $1$ の直交座標系を適当な向きに向けたものである。
3つのベクトル $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を大きさ $1$ のベクトルとし、それらを第1列目、第2列目、第3列目に持つ行列を $R$ とし、以下簡単に $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ のように書き表す。
$R$ を回転行列とするとき、これら3つのベクトルが3D空間内においてそれぞれどういった関係になっているかについては上記の3つの性質 $(\mathrm{i})$、$(\mathrm{ii})$、$(\mathrm{iii})$ から次のように決定される。
まず第1列目の $\boldsymbol{\mathsf{u}}$ はどの方向でもよいので適当に定め、図8に示される方向のベクトルとする。ただし性質 $(\mathrm{i})$ によりその大きさは $1$ である。第2列目のベクトル $\boldsymbol{\mathsf{v}}$ は性質 $(\mathrm{ii})$ によって $\boldsymbol{\mathsf{u}}$ と直交する単位ベクトルでなければならない。$\boldsymbol{\mathsf{u}}$ とのなす角が $90^\circ$ になるような方向は無数にあるがその1つを適当にとってその方向を $\boldsymbol{\mathsf{v}}$ とする (図9 ; $\boldsymbol{\mathsf{u}}$ を法線ベクトルとして持つ平面上のベクトルであれば、どのベクトルであっても $\boldsymbol{\mathsf{u}}$ と直交する)。
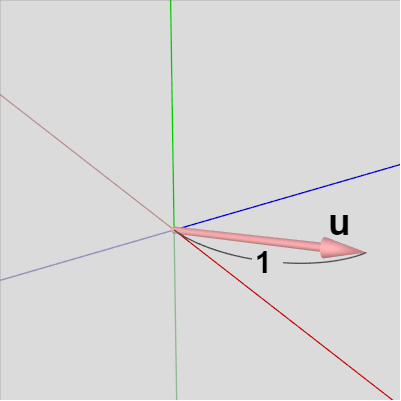
図8 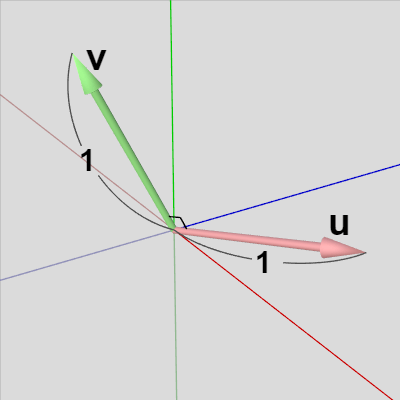
図9 u と v は互いに直交する単位ベクトル
再び性質 $(\mathrm{i})$、$(\mathrm{ii})$ によって第3列目のベクトル $\boldsymbol{\mathsf{w}}$ も、$\boldsymbol{\mathsf{u}}$ 及び $\boldsymbol{\mathsf{v}}$ と直交する単位ベクトルでなければならないが、下図10に示されるように $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$ と直交する方向は2つあり、ここではそれらを $\boldsymbol{\mathsf{w_1}}$、$\boldsymbol{\mathsf{w_2}}$ で表す。
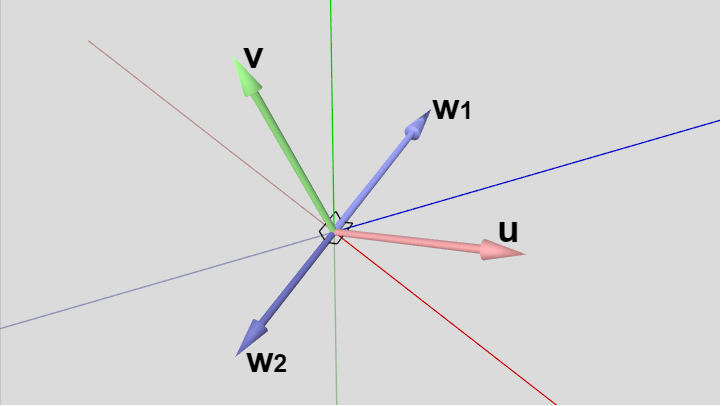
図10 u、v の両方と直交する方向は2つあり、ここでは w1、w2 としている。
ここで $\boldsymbol{\mathsf{w_1}}$、$\boldsymbol{\mathsf{w_2}}$ のうちどちらを第3列目の $\boldsymbol{\mathsf{w}}$ とするかということが問題になるが、それは性質 $(\mathrm{iii})$ を使って次のように決定される。
回転行列 $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ の行列式 $det R$ はスカラー三重積によって\[ det R = det(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}}) = \boldsymbol{\mathsf{w}}\cdot(\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}})\]と表される。$\boldsymbol{\mathsf{w}}$ の大きさは $1$ であり、$\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$ は直交しているので外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ の大きさも $1$ である。したがって $\boldsymbol{\mathsf{w}}$ と $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ のなす角を $\theta$ とすれば、\[detR = \boldsymbol{\mathsf{w}}\cdot(\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}) = |\boldsymbol{\mathsf{w}}||\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}|\cos\theta = \cos\theta\]である。$detR = 1$ であれば $\cos\theta = 1$、すなわち $\theta = 0^\circ$ であるから、行列式が $1$ であるとは外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ が同じ方向を向いていることを意味しているわけである。外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ の方向は(左手系の場合には)左手の親指を $\boldsymbol{\mathsf{u}}$ に、人差し指を $\boldsymbol{\mathsf{v}}$ に合わせたときの中指の指す方向であるが、図10において左手の親指を $\boldsymbol{\mathsf{u}}$ に人差し指を $\boldsymbol{\mathsf{v}}$ に合わせたとき、中指は $\boldsymbol{\mathsf{w_1}}$ の方向を向くから、結局第3列目の $\boldsymbol{\mathsf{w}}$ として $\boldsymbol{\mathsf{w_1}}$ を選べばよいことがわかる (回転行列の行列式が $1$ であるという性質は、簡単にいえば回転行列の1列目、2列目に親指、人差し指を合わせたときに3列目が中指の方向を向いているということである)。
回転行列 $R$ を可視化したものは最終的には図11の形になる。つまり大きさ $1$ の座標系を適当な向きに向けたものである。
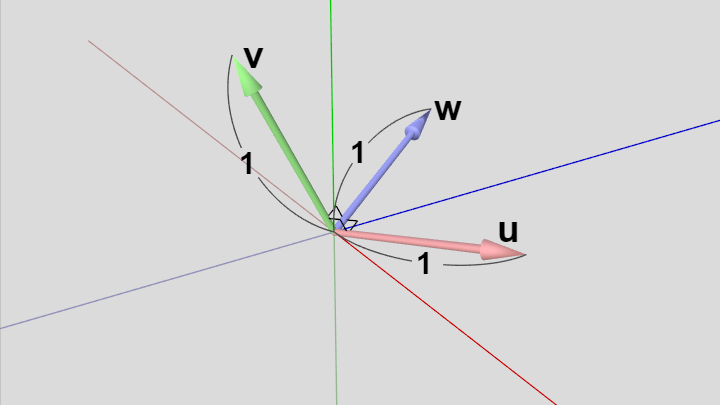
図11 回転行列 R = (u, v, w) を可視化したもの。R の各列は互いに直交しており、その大きさはいずれも 1。さらに第1列目 u、第2列目 v に左手の親指、人差し指を合わせると中指は第3列目の w の方向を向く。これは R の行列式が 1 であることを意味する。
では今述べたことに関連して回転行列(あるいは回転それ自体)を別の視点で捉えよう。
図12はあるオブジェクトの初期状態であり、初期状態において原点に位置している部分を3-9節と同様にオブジェクト原点と呼ぶことにする。このオブジェクトにはその上部に緑の印が、前方に青い印がついているが、オブジェクト原点から緑の印への方向を「オブジェクトの上方向」と呼ぶことにする。また、オブジェクト原点から青い印への方向を「オブジェクトの向き」と呼ぶことにする (図13 ; 図における緑のベクトルが上方向、青いベクトルが向きを表している)。
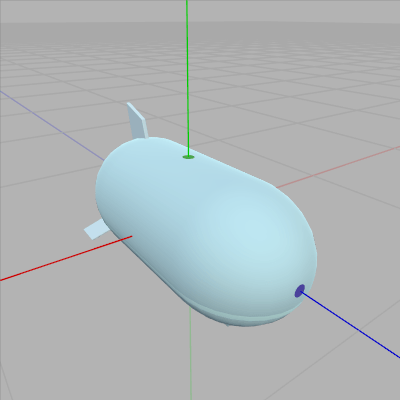
図12 オブジェクトの初期状態。緑の印はオブジェクトの上部にあり、y軸とオブジェクトの交点部分。青い印はオブジェクトの前方にあり、z軸とオブジェクトの交点部分。 
図13 緑のベクトルが上方向、青いベクトルが向きを表す。初期状態においては上方向が +y軸方向、向きが +z軸方向である。
図に示されるように初期状態における上方向は +y 軸方向、向きは +z 軸方向である。つまりこのオブジェクトには初期状態において上方向及び向きが $(0, 1, 0)$、$(0, 0, 1)$ として定められているわけである。
ここで直交する2つの単位ベクトル $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を適当な方向に定める (図14)。このとき上図13の状態のオブジェクトに対し適当な回転を実行し、オブジェクトの上方向が $\boldsymbol{\mathsf{v}}$、向きが $\boldsymbol{\mathsf{w}}$ に一致するような回転行列(図13の状態から図15の状態にする回転行列)を考えよう。
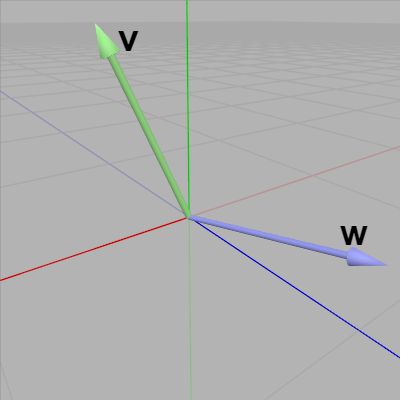
図14 v、w は互いに直交する単位ベクトル 
図15 オブジェクトの上方向が v に、向きが w に一致している
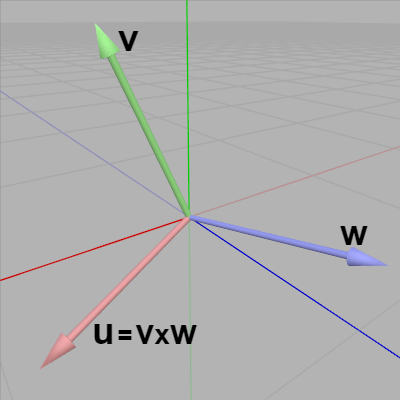
図16 u、v、w は互いに直交する単位ベクトルであり、さらに u、v に左手の親指、人差し指を合わせると中指は w の方向を指す。 それは次のように一意的に決定される。つまり $\boldsymbol{\mathsf{v}}\times\boldsymbol{\mathsf{w}} = \boldsymbol{\mathsf{u}}$ とし、$R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ とするだけである (図16)。
実際、$\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ の大きさがそれぞれ $1$ であり、互いに直交することは明らかである。また上で述べたように回転行列の行列式が $1$ であるとは、回転行列の第1列目、第2列目に(左手の)親指、人差し指を合わせたときに第3列目が中指の方向を指しているということであった。この場合は $R$ の第1列目、第2列目、第3列目は $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ であるから、図16の $\boldsymbol{\mathsf{u}}$ に親指を、$\boldsymbol{\mathsf{v}}$ に人差し指を合わせると中指が確かに $\boldsymbol{\mathsf{w}}$ の方向を向くので $R$ の行列式は $1$ であり、すなわち $R$ は回転行列であることがわかる。
そしてオブジェクトの初期状態(図13)では上方向は $(0, 1, 0)$、向きは $(0, 0, 1)$ であるから、\begin{align*}R\begin{pmatrix}0\\1\\0\end{pmatrix}=(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})\begin{pmatrix}0\\1\\0\end{pmatrix}= \boldsymbol{\mathsf{v}} \\\\R\begin{pmatrix}0\\0\\1\end{pmatrix}=(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})\begin{pmatrix}0\\0\\1\end{pmatrix}= \boldsymbol{\mathsf{w}} \\\\\end{align*}となる。したがって、回転行列 $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ はオブジェクトを図13の状態から図15の状態に変化させる回転行列である。
これは初期状態においてオブジェクトの上方向及び向きが決められている状況では、(別の)上方向及び向き $(\boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ を定めることで、それらの方向にオブジェクトを向けさせる回転行列が $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ として一意的に決定されることを意味する。つまり、1組の上方向及び向きを定めれば1つの回転が決定されるわけである。
逆に1つの回転行列 $R' = (\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')$ が与えられたとき、この回転行列を初期状態のオブジェクト(図13)に実行するとオブジェクトの上方向及び向きはこの回転によって $\boldsymbol{\mathsf{v}}'$、$\boldsymbol{\mathsf{w}}'$ になることは以下の計算から明らかである。
\begin{align*}R'\begin{pmatrix}0\\1\\0\end{pmatrix}=(\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')\begin{pmatrix}0\\1\\0\end{pmatrix}= \boldsymbol{\mathsf{v}}' \\\\R'\begin{pmatrix}0\\0\\1\end{pmatrix}=(\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')\begin{pmatrix}0\\0\\1\end{pmatrix}= \boldsymbol{\mathsf{w}}' \\\\\end{align*}これは初期状態においてオブジェクトの上方向及び向きが(上図13のように)決められている状況では、ある1つの回転行列 $R' = (\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')$ をオブジェクトに実行することで、オブジェクトの上方向及び向きは一意的に $\boldsymbol{\mathsf{v}}'$、$\boldsymbol{\mathsf{w}}'$ に変化することを意味する。つまり、1つの回転を定めれば1組の上方向及び向きが決定されるわけである。
以上のことから初期状態においてオブジェクトの上方向及び向きが決められている状況では、ある1組の上方向及び向きとある1つの回転行列は1対1に対応することがわかる。簡潔な形でいえば、1組の上方向及び向きを指定することはある1つの回転を指定することと同じなのである。
回転に対するこのような見方はカメラの姿勢制御などでは特に重要である。また、後に扱うオイラー角なども回転をこのように捉えることでその意味が明らかになるのである。
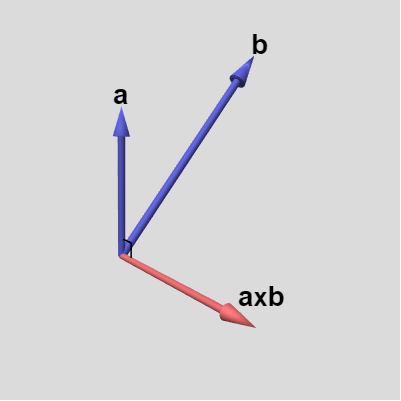
図17 a, b の外積 a x b そして外積 $\boldsymbol{a} \times \boldsymbol{b}$ は2つのベクトル $\boldsymbol{a}$、$\boldsymbol{b}$ と直交し、その向きは(左手系の場合には) $\boldsymbol{a}$ に左手の親指を、$\boldsymbol{b}$ に人差し指を合わせたときの左手の中指の指す方向として定義されたのであった。そして、そこで述べたように上記の $\boldsymbol{a} \times \boldsymbol{b}$ が $\boldsymbol{a}$ や $\boldsymbol{b}$ と直交することを示すのは容易であり、それはただ内積を計算すればよい。
しかし上記の成分で表されるベクトルが定義通りの方向を向いているか、すなわち左手の親指を $\boldsymbol{a}$ に、人差し指を $\boldsymbol{b}$ に合わせたときの左手の中指の指す方向になっているかについては内積を計算しただけではわからない。
ここでは任意軸周りの回転行列を用いて、この外積の向きの問題について考えていこう。
$\boldsymbol{a}$、$\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ の向きが左手の中指の指す方向になっているかを調べるために、以下では任意軸回転によって外積を'構成'する。
$\boldsymbol{a} = (a_x, a_y, a_z)$ を単位ベクトルとし、$\boldsymbol{b} = (b_x, b_y, b_z)$ を $0$ ではない任意の大きさのベクトル、2つのベクトルのなす角を $\theta$ とする (図18)。さらに $\boldsymbol{a}$、$\boldsymbol{b}$ と同じ平面上に $\boldsymbol{a}$ と直交するベクトル $\boldsymbol{c}$ を図19に示されるように定める。このとき $\boldsymbol{c}$ は適当な $t$ ($t > 0$)を用いて、$\boldsymbol{c} = t\boldsymbol{b} - \boldsymbol{a}$ と表される。
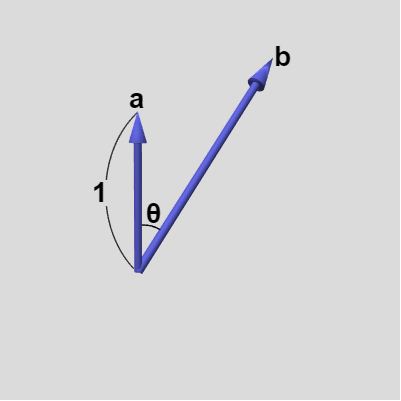
図18 a は単位ベクトル 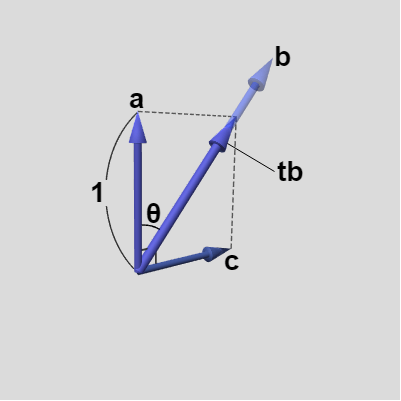
図19 b は単位ベクトルではないので、tb における t は長さではなく倍率である (t > 0)
$|\boldsymbol{a}| = 1$ であり、$\boldsymbol{a}$ と $\boldsymbol{b}$ のなす角が $\theta$ であるから、下図20に示されるように、\[ \boldsymbol{a}\cdot t\boldsymbol{b} = t(\boldsymbol{a}\cdot\boldsymbol{b}) = t|\boldsymbol{a}||\boldsymbol{b}|cos\theta = 1 \]である (図は $0 < \theta < 90^\circ$ の場合であるが、$90^\circ < \theta < 180^\circ$ であれば $t(\boldsymbol{a}\cdot\boldsymbol{b}) = -1$、$\boldsymbol{c} = t\boldsymbol{b} + \boldsymbol{a}$ であり、$\theta = 90^\circ$ の場合は $t$ は必要ないので $\boldsymbol{a}\cdot\boldsymbol{b} = 0$、$\boldsymbol{c} = \boldsymbol{b}$ となる)。
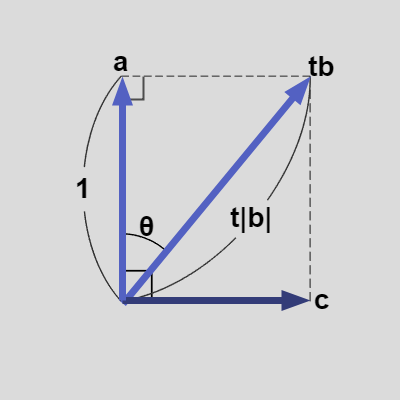
図20 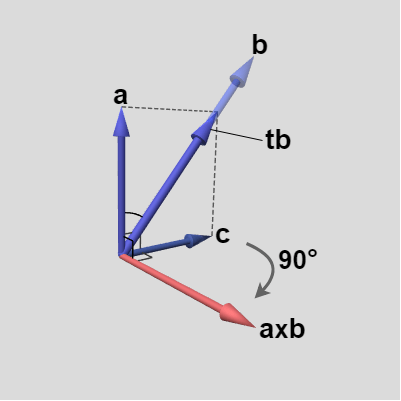
図21 a を回転軸として c を90°回転させると、a x b と同じ方向になる
$\boldsymbol{a}$ と $\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ の向きは左手の親指を $\boldsymbol{a}$ に、人差し指を $\boldsymbol{b}$ に合わせたときの中指の指す方向であるが、それは図21に示されるように、$\boldsymbol{a}$ を回転軸としてベクトル $\boldsymbol{c}$ を $90^\circ$ 回転させた方向に等しい。したがって、軸 $\boldsymbol{a}$ 周りの $90^\circ$ の回転を表す回転行列と $\boldsymbol{c}$ の積を計算すれば外積 $\boldsymbol{a} \times \boldsymbol{b}$ の方向が求められるわけである。
上で見たように、単位ベクトル $\boldsymbol{n} = (n_x, n_y, n_z)$ を回転軸とする角度 $\theta$ の回転を表す行列は
あとはこの回転行列と $\boldsymbol{c} = t\boldsymbol{b} - \boldsymbol{a}$ の積を計算すればよいが、この回転によって $\boldsymbol{a}$ は変化しないことと、$t(\boldsymbol{a}\cdot\boldsymbol{b}) = 1$ に注意すれば、この積は以下ように計算される。
(注意 : 以前上で述べたことに関して、冒頭の任意軸周りの回転行列はロドリゲスの回転公式から導出されるものであり、ロドリゲスの回転公式は外積が中指の方向を向くことを前提として得られるものであるから、この回転行列を使って外積の向きに関する証明を行うことは循環論法になるためできないと述べた。確かにこの回転行列をロドリゲスの公式経由で導出したという立場を取るならば、外積の向きに関する証明としては使うことはできない。
しかし、この回転行列はロドリゲスの回転公式を使わない方法で導出することができる。言い換えれば外積とは無関係に導出することができるので、そういった立場を取るならば上記の外積の'構成'を外積の向きに関する証明として使うことには何の問題もない。
詳しい導出に関しては右のリンクを参照 (計算の詳細)。より一般の形での証明については14-1節参照。)
ここからは、本節で述べた内容に関してのプログラムを作成する。
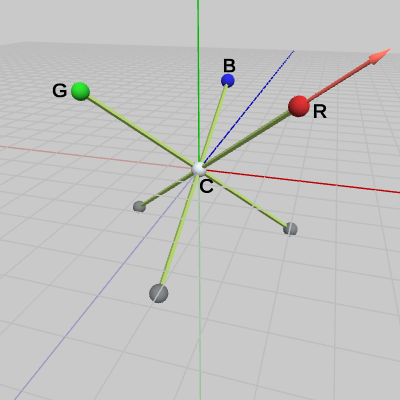
図2 初期状態のTrinoとCR軸 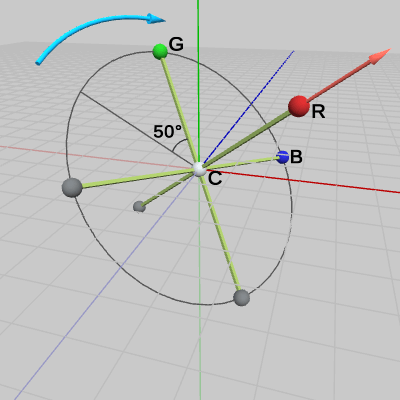
図4 CR軸周りに50°の回転
[Code1] (実行結果 図4)

図5 第1の回転実行後のTrinoとCG軸 
図7 CG軸周りの回転
[Code2] (実行結果 図7)
(ⅰ) 各列は大きさが$1$である
(ⅱ) 各列は互いに直交している (任意の2つの列同士の内積が$0$になる)
(ⅲ) 行列式が$1$である
前節、及び本節のプログラム中においては、回転行列を取得するためにカスタムライブラリの以下のメソッドを使用した。
このメソッドから取得される回転行列が上記の3つの性質を満たしているかをプログラムによって確かめてみよう。
[Code3] (実行結果 図22、図23、図24)
このプログラムは TH3DMath.GetRotation4x4(..) から取得された回転行列について、各列の大きさ、各列の間での内積、その行列の行列式を表示するものである。8~10行目のc1、c2、c3が回転行列の第1列目、第2列目、第3列目を表し、11~13行目のmag1、mag2、mag3がそれらの列の大きさを表している (第4列目の大きさは以下に示される行列から、明らかに$1$であることがわかる)。14~16行目のdot12、dot13、dot23は1列目と2列目の内積、1列目と3列目の内積、2列目と3列目の内積を表している。ここで取得される回転行列Rは $4\times4$行列であるから第4列目も存在するが、第4列目との内積は確かめる必要はない。実際、本節冒頭で見たように任意軸回転を表す$4\times4$行列は次の形をしている。
\[\begin{pmatrix}r_{11} &r_{12} &r_{13} &0\\r_{21} &r_{22} &r_{23} &0\\r_{31} &r_{32} &r_{33} &0\\0 &0 &0 &1\end{pmatrix}\]第4列目は $(0, 0, 0, 1)$ である。この第4列目と他の列、例えば第1列目との内積は以下に示されるように$0$である。\[ r_{11}\cdot 0 + r_{21}\cdot 0 + r_{31}\cdot 0 + 0\cdot 1 = 0 \]この結果は第2列目との内積、第3列目との内積でも同様である。つまり、(同次座標に対応した)$4\times4$回転行列の第4列目と他の列の内積は上記からわかるように常に$0$である。そのため、$4\times4$回転行列の各列が直交しているかを確かめるためには、第1列目から第3列目の間で内積を計算すればよい。
17行目の determinant は行列式を表すMatrix4x4構造体のプロパティであり、R.determinant は回転行列Rの行列式を意味する。
以下は、1~6行目に示される3つの回転行列のそれぞれの実行結果である。
(1)の回転行列は $(3, 4, 5)$ の方向を回転軸とし、$100$°の回転を行うものである。
(2)の回転行列は $(-11.53,\ 28.2,\ 40.65)$ の方向を回転軸とし、$85.28$°の回転を行うものである。
(3)の回転行列は $(802.22,\ -459.51,\ -363.84)$ の方向を回転軸とし、$-24.56$°の回転を行うものである。
図23、図23、図24はそれぞれの実行結果であるが、いずれの場合も各列の大きさは $1$ であり、各列の間の内積は $0$、そして行列式は $1$ という結果になっている (出力は小数第3位までの表示)。
3D空間内に下図に示されるような円周が置かれている。この円周を円盤とみなしたとき、図中の線分 $AB$ は円盤の中心を通り、さらに円盤と直交する。
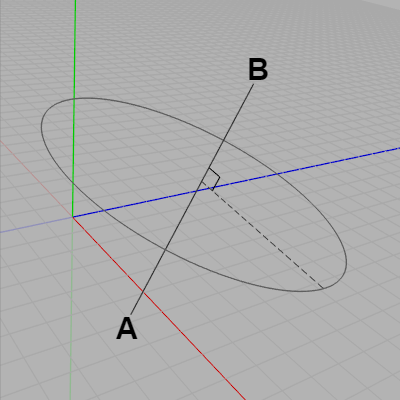
図25 円周と回転軸 AB 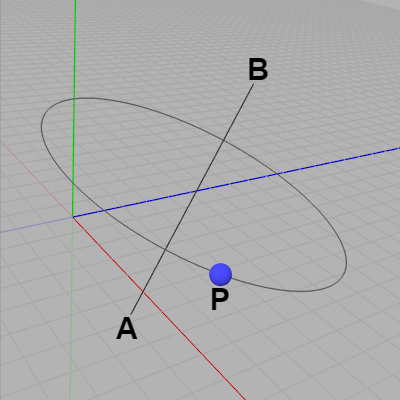
図26 Pの位置から回転させる
ここでの課題はこの円周上の $P$ の位置に置かれた球体(図26)を線分 $AB$ を回転軸として毎フレーム $1^\circ$ ずつ回転させることである (結果的に球体が円周上を移動していくことになる)。
プログラムに用意されている定数及びインスタンス変数は以下のとおり。
プログラムはCode4に作成するものとする。上記の球体はプログラム内では Ball というオブジェクトとして使われており、最初の段階では初期化ブロック内で Ball を $P$ へ移動させる処理のみが記述されている。
[Code4]
Ballの置かれる位置を指定する際は上記のように Ball.SetWorldPosition(pos) とすればよい。現時点でのBallの位置を取得する場合には Ball.GetWorldPosition() とすればよい。また本節中でも述べたが、任意軸周りの回転行列は TH3DMath.GetRotation4x4(deg, axis) によって取得できる (deg にはラジアンではなく度数法による角度を指定し、axis には回転軸を指定する)。
(解答例のプログラムは Sec311_Ans.txt を参照)

図27 2つのベクトル $V_1$、$V_2$ (大きさは同じ) 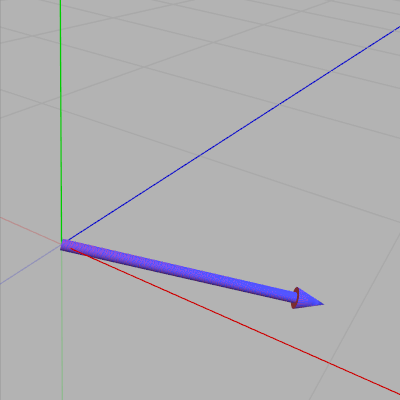
図28 $V_1$ に回転を実行し、$V_2$ に一致させる (Code5 実行結果)
ここでの課題は図27のベクトル $V_1$ に適当な回転行列を実行し、$V_2$ に一致させることである。ただし回転行列を求める際には角度を算出する逆関数(Acos や Asin など)を使わないものとする (また $V_1$ と $V_2$ の中間ベクトルを回転軸とする $180^\circ$ 回転もここでは対象外とする)。
プログラムには以下の定数が用意されている。
プログラムはCode5に作成するものとし、$V_1$ の回転は S キーが押された際に行われるものとする。
[Code5] (実行結果 図28)
今回は自前で回転行列を作成する必要がある。冒頭でも述べたが Matrix4x4 型のインスタンスをコンストラクタ経由で作る場合は $4\times 4$ 行列の各列を引数にセットする (行ではない)。各列を c1、c2、c3、c4 とすれば new Matrix(c1, c2, c3, c4) とすればよい (c1~c4 は Vector4型)。
今回は平行移動は必要ないので第4列目は $(0, 0, 0, 1)$ のままでよい。したがって上のプログラムにおける4~6行目の a、b、c、d、e、f、g、h、i を適当に書き換えて目的の行列を作ることが今回の課題である。
適切な回転行列が10行目の RotateV1(..) にセットされれば、$V_1$ を $V_2$ に一致させる回転が行われ図28のような結果になる (C キーが押されると回転前の状態に戻る)。
今回の課題では角度を使うことができない。しかしベクトルの内積によって $\cos$ が、外積によって $\sin$ がわかるので自ずと答えは出るであろう。もし読者がこの制限でも余裕であれば、さらに平方根を使わないという制限を追加するとよい (この場合 magnitude や normalized のようなプロパティも使うことはできない)。問題としてはそちらの方が面白いはずである。
(解答例のプログラムは Sec311_Ans.txt を参照)。
A) 任意軸回転を表す行列
次の行列は、ロドリゲスの回転公式(Rodrigues' rotation formula)という公式から得られるもので、3D空間において原点を通る任意の軸の周りの回転を表す行列である。単位ベクトルで表された回転軸 $\boldsymbol{n} = (n_x, n_y, n_z)$ の周りに角度 $\theta$ だけ回転させる行列($3\times 3$行列)
\[\begin{pmatrix}n_x^2(1-\cos\theta) + \cos\theta &n_xn_y(1-\cos\theta) - n_z\sin\theta &n_xn_z(1-\cos\theta) + n_y\sin\theta \\n_xn_y(1-\cos\theta) + n_z\sin\theta &n_y^2(1-\cos\theta) + \cos\theta &n_yn_z(1-\cos\theta) - n_x\sin\theta \\n_xn_z(1-\cos\theta) - n_y\sin\theta &n_yn_z(1-\cos\theta) + n_x\sin\theta &n_z^2(1-\cos\theta) + \cos\theta \end{pmatrix}\]
同次座標に対応させるために$4\times4$行列で表した場合
\[\begin{pmatrix}n_x^2(1-\cos\theta) + \cos\theta &n_xn_y(1-\cos\theta) - n_z\sin\theta &n_xn_z(1-\cos\theta) + n_y\sin\theta &0\\n_xn_y(1-\cos\theta) + n_z\sin\theta &n_y^2(1-\cos\theta) + \cos\theta &n_yn_z(1-\cos\theta) - n_x\sin\theta &0\\n_xn_z(1-\cos\theta) - n_y\sin\theta &n_yn_z(1-\cos\theta) + n_x\sin\theta &n_z^2(1-\cos\theta) + \cos\theta &0\\0 &0 &0 &1\end{pmatrix}\]
次のプログラムは前節でも使用した、カスタムライブラリーの回転行列を取得するメソッド TH3DMath.GetRotation4x4(float deg, Vector3 axis) である。このメソッドは上記の行列をそのまま実装しているので任意軸回転にも対応している。
[GetRotation4x4]
public static Matrix4x4 GetRotation4x4(float deg, Vector3 axis)
{
Vector3 n = axis.normalized;
float nx = n.x;
float ny = n.y;
float nz = n.z;
float theta = Mathf.Deg2Rad * deg;
float cosT = Mathf.Cos(theta);
float sinT = Mathf.Sin(theta);
Vector4 c1 = new Vector4( // column1
nx * nx * (1 - cosT) + cosT, nx * ny * (1 - cosT) + nz * sinT, nx * nz * (1 - cosT) - ny * sinT, 0.0f
);
Vector4 c2 = new Vector4( // column2
nx * ny * (1 - cosT) - nz * sinT, ny * ny * (1 - cosT) + cosT, ny * nz * (1 - cosT) + nx * sinT, 0.0f
);
Vector4 c3 = new Vector4( // column3
nx * nz * (1 - cosT) + ny * sinT, ny * nz * (1 - cosT) - nx * sinT, nz * nz * (1 - cosT) + cosT, 0.0f
);
Vector4 c4 = new Vector4(0.0f, 0.0f, 0.0f, 1.0f); // column4
return new Matrix4x4(c1, c2, c3, c4);
}
注意すべき点は、Unityでは行列を作成する際には引数に列をセットしなければならない。この場合では22行目の new Matrix4x4(c1, c2, c3, c4) の4つの引数には、それぞれ第1列目から第4列目を表すVector4データが渡されているのである。c1、c2、c3、c4は行列の各列を表すデータである(行ではない)。
なお、このメソッドの第2引数axisには回転軸を表すベクトルをセットするが、これは単位ベクトルでなくても構わない。このメソッドの冒頭で正規化されるからである。

B) オブジェクトに任意軸周りの回転行列を実行する
図1には、オブジェクトTrinoが初期状態で置かれている。このオブジェクトの中心は図中のCで表されている白い球で、この球の中心は原点に一致している。この中心の球から(y軸方向の)上下に3本ずつ腕が出ており、上側に出ている腕の先にはR、G、Bと表示のついている3つの球がある。また、各腕の長さはみな等しく、各腕は互いに直交している。
では、このオブジェクトTrinoに任意軸周りの回転行列を実行していこう。
まず始めに、CからRの方向を回転軸として、この軸の周りに$50$°の回転を行う。図2における淡い赤色のベクトルは、この回転軸を表している(オブジェクトと重なっているため見えないが、このベクトルは原点を始点としている)。
 図2 C--R方向を表す回転軸(始点は原点)
図2 C--R方向を表す回転軸(始点は原点)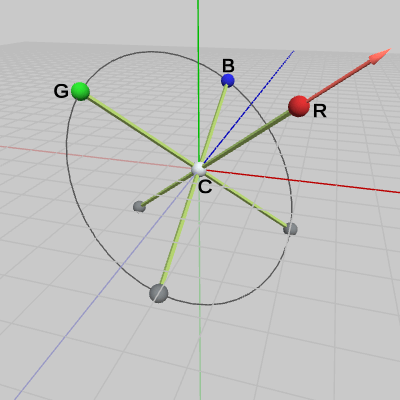 図3 GやBが回転する円周
図3 GやBが回転する円周 図4 C--R周りの50°の回転
図4 C--R周りの50°の回転
Trinoの中心Cから出ている各腕の長さは等しく、互いに直交している。したがって、腕CG、CBは腕CRと直交している。さらに、長さについては CG = CB である。前節で述べたように、ある点を回転軸の周りに回転させることは、その点から回転軸へ垂線を下ろしたときの、垂線の足を中心とし、垂線の長さを半径とする円周上の回転に等しくなる。球G、Bを点とみれば、今回の場合は腕CG、CBは腕CRと直交しているので、それらの腕は点G、Bから回転軸へ下ろされた垂線とみなすことができる(球Cを点と考えれば、垂線の足が点Cである)。そしてCG、CBは長さが等しいので点G、Bが回転する円周は全く同じものになる(図3)。
オブジェクトTrinoに、上記の回転を実行するプログラムを以下に示す。
Vector3 posR = new Vector3(2.8284f, 2.4495f, -1.4142f); Matrix4x4 rotCR = TH3DMath.GetRotation4x4(50.0f, posR); // C--R周りの回転 Trino.SetMatrix(rotCR);
posR は球Rの(中心の)位置を表している。2行目の回転行列を取得するメソッドの第2引数には、回転軸を表すベクトルをセットするが、ここではposRが使われている。回転軸を表すベクトルは球Cから球Rの方向を表すベクトルなので、球Cの(中心の)位置を Center とすれば、CからRの方向は (posR - Center) である。Center は上で述べたように原点なので結局、(posR - Center) = posR となり、posRが回転軸を表すベクトルとして使われているのである。
このプログラムの実行結果は図4に示されている。
では次に、上記の回転をした状態のTrinoに対して、今度はCからGの方向を回転軸として、この軸の周りの回転を実行しよう(図5)。ここで注意すべきことは最初の回転でGの位置は動いているため、まず、Gの回転後の位置を求める必要がある。
ただし、これは次のように簡単に求めることができる。
Vector3 posR = new Vector3(2.8284f, 2.4495f, -1.4142f); Vector3 posG = new Vector3(-2.8284f, 2.4495f, -1.4142f); Matrix4x4 rotCR = TH3DMath.GetRotation4x4(50.0f, posR); // C--R周りの回転 Vector3 posG1 = rotCR * posG;

したがって回転後のCからGの方向とは、上記の Center を再び使えば (posG1 - Center)、すなわち posG1 である。このposG1が、次の回転における回転軸を表すベクトルとして使われることになる(posG1は図5におけるGの位置を表す)。
以下では便宜上、最初の回転における回転軸をCR軸、第2の回転における回転軸をCG軸と表記する。
今回のプログラムは最初の回転後の状態から、CG軸周りに毎フレーム1°ずつ回転し続けるプログラムである(プログラム中のインスタンス変数i_degRotは回転角度を表し、毎フレーム$1$ずつ増加する)。
Vector3 posR = new Vector3(2.8284f, 2.4495f, -1.4142f); Vector3 posG = new Vector3(-2.8284f, 2.4495f, -1.4142f); Matrix4x4 rotCR = TH3DMath.GetRotation4x4(50.0f, posR); // CR軸周りの回転 Vector3 posG1 = rotCR * posG; i_degRot++; Matrix4x4 rotCG = TH3DMath.GetRotation4x4(i_degRot, posG1); // CG軸周りの回転 // CR軸周りに回転させてからCG軸周りに回転させる Matrix4x4 R = rotCG * rotCR; Trino.SetMatrix(R);
4行目までの処理は上で述べた通りである。最初の回転後の状態におけるCG軸を表すベクトルがposG1であり、7行目で回転行列を取得する際の回転軸を表す引数として、posG1をセットすることでCG軸周りの回転行列rotCGが得られる。ただし、このrotCGをそのままTrinoにセットしても意味がない。
今回実装する回転は、最初の回転後の状態から、CG軸周りに回転させなければならない。具体的には、図5の状態からCG軸周りに回転させることが必要なのである。もし、Trinoに行列をセットする際に上記の10~11行目を次のように書き換えて、
Trino.SetMatrix(rotCG);
7行目で取得した回転行列rotCGは、図5におけるTrinoのCG軸周りの回転であるので、毎フレーム、Trinoをまず図5の状態にしてからrotCGを実行しなければ意味がないのである。「図5の状態にする」とは、最初の回転であるCR軸周りの$50$°の回転を実行することである。これはプログラムの3行目で取得される回転行列rotCRを実行すればよい。
つまり、最初の回転後の状態からCG軸周りに回転させるためには、毎フレームTrinoにrotCRを実行し、その後にrotCGを実行しなければならない。10~11行目の処理がそれにあたるわけである。
// CR軸周りに回転させてからCG軸周りに回転させる Matrix4x4 R = rotCG * rotCR; Trino.SetMatrix(R);


今回の回転軸である腕CGと腕CR、CBは直交しており、長さについては CR = CB である。最初の回転の箇所でも説明したが、この場合にはR、Bの回転軌道は同じものになる(図6)。
図7は、CG軸周りの回転プログラムの実行結果である。
C) 直交行列
回転行列は詳しくは直交行列(Orthogonal Matrix)という行列の一種である。ここではこの直交行列について簡単に述べておこう。行列 $A$ が次の関係を満たすとき、$A$を直交行列という (以下の $A^T$ は $A$ の転置行列で、$I$ は単位行列(identity行列))。
\[A^TA = AA^T = I \]これは、直交行列 $A$ の転置行列 $A^T$ は $A$ の逆行列であることを意味する。すなわち、
\[A^T = A^{-1}\]である(逆行列については3-7節、転置行列については3-8節参照)。
先に述べた通り、回転行列も直交行列の一種であるから回転行列もこの性質を持っている。つまり、回転行列の逆行列を求めるには、その回転行列を転置すればよいのである。
(例)
y軸周りに角 $\theta$ 回転させる行列 $R_y$ とその転置行列である $R_y^T$ の積を計算してみよう。
\[R_y = \begin{pmatrix}\cos\theta &0 &\sin\theta\\0 &1 &0\\-\sin\theta &0 &\cos\theta\\\end{pmatrix}\qquad R_y^T = \begin{pmatrix}\cos\theta &0 &-\sin\theta\\0 &1 &0\\\sin\theta &0 &\cos\theta\\\end{pmatrix}\]
\begin{align*}R_yR_y^T &= \begin{pmatrix}\cos\theta &0 &\sin\theta\\0 &1 &0\\-\sin\theta &0 &\cos\theta\\\end{pmatrix}\begin{pmatrix}\cos\theta &0 &-\sin\theta\\0 &1 &0\\\sin\theta &0 &\cos\theta\\\end{pmatrix}\\\\&=\begin{pmatrix}\cos\theta^2 + 0 + \sin\theta^2 &\cos\theta\cdot0 + 0 + \sin\theta\cdot0 &\cos\theta(-\sin\theta) + 0 + \sin\theta\cdot\cos\theta\\0\cdot\cos\theta + 0 + 0\cdot\sin\theta &0 + 1 + 0 &0\cdot(-\sin\theta) + 0 + 0\cdot\cos\theta\\\cos\theta(-\sin\theta) + 0 + \cos\theta\sin\theta &-\sin\theta\cdot0 + 0 + \cos\theta\cdot0 &(-\sin\theta)^2 + 0 + \cos\theta^2\end{pmatrix}\\\\&=\begin{pmatrix}1 &0 &0\\0 &1 &0\\0 &0 &1\end{pmatrix}\end{align*}
$R_y$ の転置行列 $R_y^T$ が、確かに $R_y$ の逆行列になっている。これは、積の順序を入れ替えても同じ結果になる。また、同次座標用の $4\times4$ 行列で計算した場合の結果は、もちろん $4\times4$ の 単位行列(identity行列)である。
詳しい証明は省くが上の定義から、直交行列の各列について次の性質が導かれる。
| ($\mathrm{i}$) | 直交行列の各列は大きさが $1$ である |
| ($\mathrm{ii}$) | 直交行列の各列は互いに直交している (任意の2つの列同士の内積が $0$ になる) |
たとえば、次の行列 $M$ が直交行列であるとしよう。\[ M = \begin{pmatrix}m_{11} &m_{12} &m_{13} &m_{14}\\m_{21} &m_{22} &m_{23} &m_{24}\\m_{31} &m_{32} &m_{33} &m_{34}\\m_{41} &m_{42} &m_{43} &m_{44}\end{pmatrix}\] $M$ はすべての列の大きさが $1$ であり、任意の2つの列は互いに直交しているので、第1列目 $(m_{11}, m_{21}, m_{31}, m_{41})$ と第2列目 $(m_{12}, m_{22}, m_{32}, m_{42})$ の内積や、第2列目 $(m_{12}, m_{22}, m_{32}, m_{42})$ と第4列目 $(m_{14}, m_{24}, m_{34}, m_{44})$ の内積はいずれも $0$ になるということである (このことは各列だけでなく各行についても成り立つ ; 詳しくは この性質を正規直交という)。
回転行列も直交行列に属すので、回転行列についても各列の大きさが $1$ であり、各列は互いに直交するという性質は満たされる。
回転行列は直交行列ではあるが、直交行列がすべて回転行列であるかというと、そうではない。具体的には、回転行列の場合は、
| ($\mathrm{i}$) | 各列の大きさが $1$ である |
| ($\mathrm{ii}$) | 各列は互いに直交している (任意の2つの列同士の内積が $0$ になる) |
| ($\mathrm{iii}$) | 行列式が $1$ である |
つまり回転行列はこの3つの性質が満たされていなければならないのである (この3つの性質のうち1つでも欠けると回転行列にはならない ; ここに現れた「行列式」についての解説は数学的にやや深入りすることになるので省略するが、回転行列の場合における行列式が $1$ であるという性質が何を意味するかについては以下の解説を参照)。
D) 回転行列の可視化
上で述べたように回転行列には以下の3つの性質がある (以下の議論における回転行列は同次座標に対応した $4\times4$ 行列ではなく、通常の $3\times3$ 行列の方である)。| ($\mathrm{i}$) | 各列の大きさが $1$ である |
| ($\mathrm{ii}$) | 各列は互いに直交している (任意の2つの列同士の内積が $0$ になる) |
| ($\mathrm{iii}$) | 行列式が $1$ である |
ここではこの3つの性質から回転行列を目に見える形で表してみよう。
結論から先にいえば回転行列を可視化したものは大きさが $1$ の座標系、具体的には大きさが $1$ の直交座標系を適当な向きに向けたものである。
3つのベクトル $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を大きさ $1$ のベクトルとし、それらを第1列目、第2列目、第3列目に持つ行列を $R$ とし、以下簡単に $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ のように書き表す。
$R$ を回転行列とするとき、これら3つのベクトルが3D空間内においてそれぞれどういった関係になっているかについては上記の3つの性質 $(\mathrm{i})$、$(\mathrm{ii})$、$(\mathrm{iii})$ から次のように決定される。
まず第1列目の $\boldsymbol{\mathsf{u}}$ はどの方向でもよいので適当に定め、図8に示される方向のベクトルとする。ただし性質 $(\mathrm{i})$ によりその大きさは $1$ である。第2列目のベクトル $\boldsymbol{\mathsf{v}}$ は性質 $(\mathrm{ii})$ によって $\boldsymbol{\mathsf{u}}$ と直交する単位ベクトルでなければならない。$\boldsymbol{\mathsf{u}}$ とのなす角が $90^\circ$ になるような方向は無数にあるがその1つを適当にとってその方向を $\boldsymbol{\mathsf{v}}$ とする (図9 ; $\boldsymbol{\mathsf{u}}$ を法線ベクトルとして持つ平面上のベクトルであれば、どのベクトルであっても $\boldsymbol{\mathsf{u}}$ と直交する)。


再び性質 $(\mathrm{i})$、$(\mathrm{ii})$ によって第3列目のベクトル $\boldsymbol{\mathsf{w}}$ も、$\boldsymbol{\mathsf{u}}$ 及び $\boldsymbol{\mathsf{v}}$ と直交する単位ベクトルでなければならないが、下図10に示されるように $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$ と直交する方向は2つあり、ここではそれらを $\boldsymbol{\mathsf{w_1}}$、$\boldsymbol{\mathsf{w_2}}$ で表す。

ここで $\boldsymbol{\mathsf{w_1}}$、$\boldsymbol{\mathsf{w_2}}$ のうちどちらを第3列目の $\boldsymbol{\mathsf{w}}$ とするかということが問題になるが、それは性質 $(\mathrm{iii})$ を使って次のように決定される。
回転行列 $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ の行列式 $det R$ はスカラー三重積によって\[ det R = det(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}}) = \boldsymbol{\mathsf{w}}\cdot(\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}})\]と表される。$\boldsymbol{\mathsf{w}}$ の大きさは $1$ であり、$\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$ は直交しているので外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ の大きさも $1$ である。したがって $\boldsymbol{\mathsf{w}}$ と $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ のなす角を $\theta$ とすれば、\[detR = \boldsymbol{\mathsf{w}}\cdot(\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}) = |\boldsymbol{\mathsf{w}}||\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}|\cos\theta = \cos\theta\]である。$detR = 1$ であれば $\cos\theta = 1$、すなわち $\theta = 0^\circ$ であるから、行列式が $1$ であるとは外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ と $\boldsymbol{\mathsf{w}}$ が同じ方向を向いていることを意味しているわけである。外積 $\boldsymbol{\mathsf{u}}\times\boldsymbol{\mathsf{v}}$ の方向は(左手系の場合には)左手の親指を $\boldsymbol{\mathsf{u}}$ に、人差し指を $\boldsymbol{\mathsf{v}}$ に合わせたときの中指の指す方向であるが、図10において左手の親指を $\boldsymbol{\mathsf{u}}$ に人差し指を $\boldsymbol{\mathsf{v}}$ に合わせたとき、中指は $\boldsymbol{\mathsf{w_1}}$ の方向を向くから、結局第3列目の $\boldsymbol{\mathsf{w}}$ として $\boldsymbol{\mathsf{w_1}}$ を選べばよいことがわかる (回転行列の行列式が $1$ であるという性質は、簡単にいえば回転行列の1列目、2列目に親指、人差し指を合わせたときに3列目が中指の方向を向いているということである)。
回転行列 $R$ を可視化したものは最終的には図11の形になる。つまり大きさ $1$ の座標系を適当な向きに向けたものである。

では今述べたことに関連して回転行列(あるいは回転それ自体)を別の視点で捉えよう。
図12はあるオブジェクトの初期状態であり、初期状態において原点に位置している部分を3-9節と同様にオブジェクト原点と呼ぶことにする。このオブジェクトにはその上部に緑の印が、前方に青い印がついているが、オブジェクト原点から緑の印への方向を「オブジェクトの上方向」と呼ぶことにする。また、オブジェクト原点から青い印への方向を「オブジェクトの向き」と呼ぶことにする (図13 ; 図における緑のベクトルが上方向、青いベクトルが向きを表している)。


図に示されるように初期状態における上方向は +y 軸方向、向きは +z 軸方向である。つまりこのオブジェクトには初期状態において上方向及び向きが $(0, 1, 0)$、$(0, 0, 1)$ として定められているわけである。
ここで直交する2つの単位ベクトル $\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ を適当な方向に定める (図14)。このとき上図13の状態のオブジェクトに対し適当な回転を実行し、オブジェクトの上方向が $\boldsymbol{\mathsf{v}}$、向きが $\boldsymbol{\mathsf{w}}$ に一致するような回転行列(図13の状態から図15の状態にする回転行列)を考えよう。



実際、$\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ の大きさがそれぞれ $1$ であり、互いに直交することは明らかである。また上で述べたように回転行列の行列式が $1$ であるとは、回転行列の第1列目、第2列目に(左手の)親指、人差し指を合わせたときに第3列目が中指の方向を指しているということであった。この場合は $R$ の第1列目、第2列目、第3列目は $\boldsymbol{\mathsf{u}}$、$\boldsymbol{\mathsf{v}}$、$\boldsymbol{\mathsf{w}}$ であるから、図16の $\boldsymbol{\mathsf{u}}$ に親指を、$\boldsymbol{\mathsf{v}}$ に人差し指を合わせると中指が確かに $\boldsymbol{\mathsf{w}}$ の方向を向くので $R$ の行列式は $1$ であり、すなわち $R$ は回転行列であることがわかる。
そしてオブジェクトの初期状態(図13)では上方向は $(0, 1, 0)$、向きは $(0, 0, 1)$ であるから、\begin{align*}R\begin{pmatrix}0\\1\\0\end{pmatrix}=(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})\begin{pmatrix}0\\1\\0\end{pmatrix}= \boldsymbol{\mathsf{v}} \\\\R\begin{pmatrix}0\\0\\1\end{pmatrix}=(\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})\begin{pmatrix}0\\0\\1\end{pmatrix}= \boldsymbol{\mathsf{w}} \\\\\end{align*}となる。したがって、回転行列 $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ はオブジェクトを図13の状態から図15の状態に変化させる回転行列である。
これは初期状態においてオブジェクトの上方向及び向きが決められている状況では、(別の)上方向及び向き $(\boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ を定めることで、それらの方向にオブジェクトを向けさせる回転行列が $R = (\boldsymbol{\mathsf{u}}, \boldsymbol{\mathsf{v}}, \boldsymbol{\mathsf{w}})$ として一意的に決定されることを意味する。つまり、1組の上方向及び向きを定めれば1つの回転が決定されるわけである。
逆に1つの回転行列 $R' = (\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')$ が与えられたとき、この回転行列を初期状態のオブジェクト(図13)に実行するとオブジェクトの上方向及び向きはこの回転によって $\boldsymbol{\mathsf{v}}'$、$\boldsymbol{\mathsf{w}}'$ になることは以下の計算から明らかである。
\begin{align*}R'\begin{pmatrix}0\\1\\0\end{pmatrix}=(\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')\begin{pmatrix}0\\1\\0\end{pmatrix}= \boldsymbol{\mathsf{v}}' \\\\R'\begin{pmatrix}0\\0\\1\end{pmatrix}=(\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')\begin{pmatrix}0\\0\\1\end{pmatrix}= \boldsymbol{\mathsf{w}}' \\\\\end{align*}これは初期状態においてオブジェクトの上方向及び向きが(上図13のように)決められている状況では、ある1つの回転行列 $R' = (\boldsymbol{\mathsf{u}}', \boldsymbol{\mathsf{v}}', \boldsymbol{\mathsf{w}}')$ をオブジェクトに実行することで、オブジェクトの上方向及び向きは一意的に $\boldsymbol{\mathsf{v}}'$、$\boldsymbol{\mathsf{w}}'$ に変化することを意味する。つまり、1つの回転を定めれば1組の上方向及び向きが決定されるわけである。
以上のことから初期状態においてオブジェクトの上方向及び向きが決められている状況では、ある1組の上方向及び向きとある1つの回転行列は1対1に対応することがわかる。簡潔な形でいえば、1組の上方向及び向きを指定することはある1つの回転を指定することと同じなのである。
回転に対するこのような見方はカメラの姿勢制御などでは特に重要である。また、後に扱うオイラー角なども回転をこのように捉えることでその意味が明らかになるのである。
E) 応用例
3-6節で見たようにベクトル $\boldsymbol{a} = (a_x, a_y, a_z)$、$\boldsymbol{b} = (b_x, b_y, b_z)$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ は\[ \boldsymbol{a} \times \boldsymbol{b}\ =\ (a_yb_z - a_zb_y,\ a_zb_x - a_xb_z,\ a_xb_y - a_yb_x) \]として表された。
しかし上記の成分で表されるベクトルが定義通りの方向を向いているか、すなわち左手の親指を $\boldsymbol{a}$ に、人差し指を $\boldsymbol{b}$ に合わせたときの左手の中指の指す方向になっているかについては内積を計算しただけではわからない。
ここでは任意軸周りの回転行列を用いて、この外積の向きの問題について考えていこう。
$\boldsymbol{a}$、$\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ の向きが左手の中指の指す方向になっているかを調べるために、以下では任意軸回転によって外積を'構成'する。
$\boldsymbol{a} = (a_x, a_y, a_z)$ を単位ベクトルとし、$\boldsymbol{b} = (b_x, b_y, b_z)$ を $0$ ではない任意の大きさのベクトル、2つのベクトルのなす角を $\theta$ とする (図18)。さらに $\boldsymbol{a}$、$\boldsymbol{b}$ と同じ平面上に $\boldsymbol{a}$ と直交するベクトル $\boldsymbol{c}$ を図19に示されるように定める。このとき $\boldsymbol{c}$ は適当な $t$ ($t > 0$)を用いて、$\boldsymbol{c} = t\boldsymbol{b} - \boldsymbol{a}$ と表される。


$|\boldsymbol{a}| = 1$ であり、$\boldsymbol{a}$ と $\boldsymbol{b}$ のなす角が $\theta$ であるから、下図20に示されるように、\[ \boldsymbol{a}\cdot t\boldsymbol{b} = t(\boldsymbol{a}\cdot\boldsymbol{b}) = t|\boldsymbol{a}||\boldsymbol{b}|cos\theta = 1 \]である (図は $0 < \theta < 90^\circ$ の場合であるが、$90^\circ < \theta < 180^\circ$ であれば $t(\boldsymbol{a}\cdot\boldsymbol{b}) = -1$、$\boldsymbol{c} = t\boldsymbol{b} + \boldsymbol{a}$ であり、$\theta = 90^\circ$ の場合は $t$ は必要ないので $\boldsymbol{a}\cdot\boldsymbol{b} = 0$、$\boldsymbol{c} = \boldsymbol{b}$ となる)。


$\boldsymbol{a}$ と $\boldsymbol{b}$ の外積 $\boldsymbol{a} \times \boldsymbol{b}$ の向きは左手の親指を $\boldsymbol{a}$ に、人差し指を $\boldsymbol{b}$ に合わせたときの中指の指す方向であるが、それは図21に示されるように、$\boldsymbol{a}$ を回転軸としてベクトル $\boldsymbol{c}$ を $90^\circ$ 回転させた方向に等しい。したがって、軸 $\boldsymbol{a}$ 周りの $90^\circ$ の回転を表す回転行列と $\boldsymbol{c}$ の積を計算すれば外積 $\boldsymbol{a} \times \boldsymbol{b}$ の方向が求められるわけである。
上で見たように、単位ベクトル $\boldsymbol{n} = (n_x, n_y, n_z)$ を回転軸とする角度 $\theta$ の回転を表す行列は
\[\begin{pmatrix}n_x^2(1-\cos\theta) + \cos\theta &n_xn_y(1-\cos\theta) - n_z\sin\theta &n_xn_z(1-\cos\theta) + n_y\sin\theta \\n_xn_y(1-\cos\theta) + n_z\sin\theta &n_y^2(1-\cos\theta) + \cos\theta &n_yn_z(1-\cos\theta) - n_x\sin\theta \\n_xn_z(1-\cos\theta) - n_y\sin\theta &n_yn_z(1-\cos\theta) + n_x\sin\theta &n_z^2(1-\cos\theta) + \cos\theta \end{pmatrix}\]
であるが、今の場合 回転軸は $\boldsymbol{a} = (a_x, a_y, a_z)$、回転角度が $90^\circ$ であるから、この行列の $n_x$、$n_y$、$n_z$ を $a_x$、$a_y$、$a_z$ に置き換え、$\cos\theta = 0$、$\sin\theta = 1$ とすればよい。そうすると、軸 $\boldsymbol{a}$ 周りの $90^\circ$ の回転行列は\[\begin{pmatrix}{a_x}^2 &a_xa_y - a_z &a_xa_z + a_y \\ a_xa_y + a_z &{a_y}^2 &a_ya_z - a_x \\ a_xa_z - a_y &a_ya_z + a_x &{a_z}^2 \end{pmatrix}\]と表される。あとはこの回転行列と $\boldsymbol{c} = t\boldsymbol{b} - \boldsymbol{a}$ の積を計算すればよいが、この回転によって $\boldsymbol{a}$ は変化しないことと、$t(\boldsymbol{a}\cdot\boldsymbol{b}) = 1$ に注意すれば、この積は以下ように計算される。
\begin{align*}&\begin{pmatrix}{a_x}^2 &a_xa_y - a_z &a_xa_z + a_y \\ a_xa_y + a_z &{a_y}^2 &a_ya_z - a_x \\ a_xa_z - a_y &a_ya_z + a_x &{a_z}^2 \end{pmatrix}\left\{t\begin{pmatrix}b_x \\b_y \\b_z \end{pmatrix}-\begin{pmatrix}a_x \\a_y \\a_z \end{pmatrix}\right\} \\\\&= t\begin{pmatrix}{a_x}^2 &a_xa_y - a_z &a_xa_z + a_y \\ a_xa_y + a_z &{a_y}^2 &a_ya_z - a_x \\ a_xa_z - a_y &a_ya_z + a_x &{a_z}^2 \end{pmatrix}\begin{pmatrix}b_x \\b_y \\b_z \end{pmatrix}-\begin{pmatrix}a_x \\a_y \\a_z \end{pmatrix} \\\\&= t\begin{pmatrix}{a_x}^2 b_x + a_xa_yb_y + a_xa_zb_z + a_yb_z - a_zb_y \\ a_xa_yb_x + {a_y}^2 b_y + a_ya_zb_z + a_zb_x - a_xb_z \\ a_xa_zb_x + a_ya_zb_y + {a_z}^2 b_z + a_xb_y - a_yb_x \end{pmatrix}-\begin{pmatrix}a_x \\a_y \\a_z \end{pmatrix} \\\\&=t\begin{pmatrix}a_x(a_xb_x + a_yb_y + a_zb_z) \\ a_y(a_xb_x + a_yb_y + a_zb_z) \\ a_z(a_xb_x + a_yb_y + a_zb_z) \end{pmatrix}+t\begin{pmatrix}a_yb_z - a_zb_y \\ a_zb_x - a_xb_z \\ a_xb_y - a_yb_x \end{pmatrix}-\begin{pmatrix}a_x \\a_y \\a_z \end{pmatrix} \\\\&=\begin{pmatrix}a_x(t(\boldsymbol{a}\cdot\boldsymbol{b}) - 1) \\ a_y(t(\boldsymbol{a}\cdot\boldsymbol{b}) - 1) \\ a_z(t(\boldsymbol{a}\cdot\boldsymbol{b}) - 1) \end{pmatrix}+t\begin{pmatrix}a_yb_z - a_zb_y \\ a_zb_x - a_xb_z \\ a_xb_y - a_yb_x \end{pmatrix} \\\\&=t\begin{pmatrix}a_yb_z - a_zb_y \\ a_zb_x - a_xb_z \\ a_xb_y - a_yb_x \end{pmatrix}\end{align*}
この計算結果に現れたベクトルは左手の親指を $\boldsymbol{a}$ に、人差し指を $\boldsymbol{b}$ に合わせたときの左手の中指の指す方向になるように構成されたものであり、係数 $t$ は $t>0$ として定められていた。この $t$ を $1$ としたものがベクトルの外積である。(注意 : 以前上で述べたことに関して、冒頭の任意軸周りの回転行列はロドリゲスの回転公式から導出されるものであり、ロドリゲスの回転公式は外積が中指の方向を向くことを前提として得られるものであるから、この回転行列を使って外積の向きに関する証明を行うことは循環論法になるためできないと述べた。確かにこの回転行列をロドリゲスの公式経由で導出したという立場を取るならば、外積の向きに関する証明としては使うことはできない。
しかし、この回転行列はロドリゲスの回転公式を使わない方法で導出することができる。言い換えれば外積とは無関係に導出することができるので、そういった立場を取るならば上記の外積の'構成'を外積の向きに関する証明として使うことには何の問題もない。
詳しい導出に関しては右のリンクを参照 (計算の詳細)。より一般の形での証明については14-1節参照。)
ここからは、本節で述べた内容に関してのプログラムを作成する。
# Code1
最初のプログラムは本節の最初に扱ったもので、初期状態の TrinoのCR軸周りに$50$°の回転を実行する。

[Code1] (実行結果 図4)
Vector3 posR = new Vector3(2.8284f, 2.4495f, -1.4142f); Matrix4x4 rotCR = TH3DMath.GetRotation4x4(50.0f, posR); // CR軸周りの回転 Trino.SetMatrix(rotCR);
# Code2
次のプログラムも本節中で扱ったものであり、CR軸周りに$50$°の回転を行った状態の Trinoに対し、CG軸周りの回転を実行する。

[Code2] (実行結果 図7)
Vector3 posR = new Vector3(2.8284f, 2.4495f, -1.4142f); Vector3 posG = new Vector3(-2.8284f, 2.4495f, -1.4142f); Matrix4x4 rotCR = TH3DMath.GetRotation4x4(50.0f, posR); // CR軸周りの回転 Vector3 posG1 = rotCR * posG; i_degRot++; Matrix4x4 rotCG = TH3DMath.GetRotation4x4(i_degRot, posG1); // CG軸周りの回転 // CR軸周りに回転させてからCG軸周りに回転させる Matrix4x4 R = rotCG * rotCR; Trino.SetMatrix(R);
# Code3
本節において、回転行列は次の3つの性質を満たしていなければいけないと述べた。(ⅰ) 各列は大きさが$1$である
(ⅱ) 各列は互いに直交している (任意の2つの列同士の内積が$0$になる)
(ⅲ) 行列式が$1$である
前節、及び本節のプログラム中においては、回転行列を取得するためにカスタムライブラリの以下のメソッドを使用した。
// axisを回転軸として角度degだけ回転させるMatrix4x4インスタンスを返す TH3DMath.GetRotation4x4(float deg, Vector3 axis)
このメソッドから取得される回転行列が上記の3つの性質を満たしているかをプログラムによって確かめてみよう。
[Code3] (実行結果 図22、図23、図24)
// (1)
Matrix4x4 R = TH3DMath.GetRotation4x4(100, new Vector3(3, 4, 5));
// (2)
//Matrix4x4 R = TH3DMath.GetRotation4x4(85.28f, new Vector3(-11.53f, 28.2f, 40.65f));
// (3)
//Matrix4x4 R = TH3DMath.GetRotation4x4(-24.56f, new Vector3(802.22f, -459.51f, -363.84f));
Vector4 c1 = R.GetColumn(0); // 第1列目
Vector4 c2 = R.GetColumn(1); // 第2列目
Vector4 c3 = R.GetColumn(2); // 第3列目
float mag1 = c1.magnitude;
float mag2 = c2.magnitude;
float mag3 = c3.magnitude;
float dot12 = Vector3.Dot(c1, c2);
float dot13 = Vector3.Dot(c1, c3);
float dot23 = Vector3.Dot(c2, c3);
float Det = R.determinant; // 行列式
Debug.LogFormat("(1)\n(mag1 {0:f3}) (mag2 {1:f3}) (mag3 {2:f3})\n" +
"(dot12 {3:f3}) (dot13 {4:f3}) (dot23 {5:f3})\n(Det {6:f3})",
mag1, mag2, mag3, dot12, dot13, dot23, Det);
このプログラムは TH3DMath.GetRotation4x4(..) から取得された回転行列について、各列の大きさ、各列の間での内積、その行列の行列式を表示するものである。8~10行目のc1、c2、c3が回転行列の第1列目、第2列目、第3列目を表し、11~13行目のmag1、mag2、mag3がそれらの列の大きさを表している (第4列目の大きさは以下に示される行列から、明らかに$1$であることがわかる)。14~16行目のdot12、dot13、dot23は1列目と2列目の内積、1列目と3列目の内積、2列目と3列目の内積を表している。ここで取得される回転行列Rは $4\times4$行列であるから第4列目も存在するが、第4列目との内積は確かめる必要はない。実際、本節冒頭で見たように任意軸回転を表す$4\times4$行列は次の形をしている。
\[\begin{pmatrix}r_{11} &r_{12} &r_{13} &0\\r_{21} &r_{22} &r_{23} &0\\r_{31} &r_{32} &r_{33} &0\\0 &0 &0 &1\end{pmatrix}\]第4列目は $(0, 0, 0, 1)$ である。この第4列目と他の列、例えば第1列目との内積は以下に示されるように$0$である。\[ r_{11}\cdot 0 + r_{21}\cdot 0 + r_{31}\cdot 0 + 0\cdot 1 = 0 \]この結果は第2列目との内積、第3列目との内積でも同様である。つまり、(同次座標に対応した)$4\times4$回転行列の第4列目と他の列の内積は上記からわかるように常に$0$である。そのため、$4\times4$回転行列の各列が直交しているかを確かめるためには、第1列目から第3列目の間で内積を計算すればよい。
17行目の determinant は行列式を表すMatrix4x4構造体のプロパティであり、R.determinant は回転行列Rの行列式を意味する。
以下は、1~6行目に示される3つの回転行列のそれぞれの実行結果である。
-
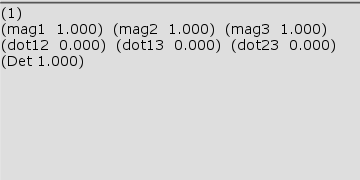 図22 Code3 実行結果 (1)
図22 Code3 実行結果 (1) -
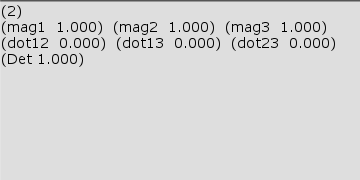 図23 Code3 実行結果 (2)
図23 Code3 実行結果 (2) -
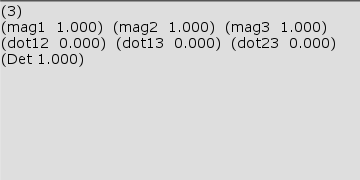 図24 Code3 実行結果 (3)
図24 Code3 実行結果 (3)
(1)の回転行列は $(3, 4, 5)$ の方向を回転軸とし、$100$°の回転を行うものである。
(2)の回転行列は $(-11.53,\ 28.2,\ 40.65)$ の方向を回転軸とし、$85.28$°の回転を行うものである。
(3)の回転行列は $(802.22,\ -459.51,\ -363.84)$ の方向を回転軸とし、$-24.56$°の回転を行うものである。
図23、図23、図24はそれぞれの実行結果であるが、いずれの場合も各列の大きさは $1$ であり、各列の間の内積は $0$、そして行列式は $1$ という結果になっている (出力は小数第3位までの表示)。
# Code4
以下2つのプログラムは読者用の課題である。3D空間内に下図に示されるような円周が置かれている。この円周を円盤とみなしたとき、図中の線分 $AB$ は円盤の中心を通り、さらに円盤と直交する。


ここでの課題はこの円周上の $P$ の位置に置かれた球体(図26)を線分 $AB$ を回転軸として毎フレーム $1^\circ$ ずつ回転させることである (結果的に球体が円周上を移動していくことになる)。
プログラムに用意されている定数及びインスタンス変数は以下のとおり。
A, B, P
: 上図の3点 $A$、$B$、$P$ (Vector3型)。i_degree
: 回転角度を表すfloat型インスタンス変数。プログラムはCode4に作成するものとする。上記の球体はプログラム内では Ball というオブジェクトとして使われており、最初の段階では初期化ブロック内で Ball を $P$ へ移動させる処理のみが記述されている。
[Code4]
if (!i_INITIALIZED)
{
Ball.SetWorldPosition(P);
i_INITIALIZED = true;
}
Ballの置かれる位置を指定する際は上記のように Ball.SetWorldPosition(pos) とすればよい。現時点でのBallの位置を取得する場合には Ball.GetWorldPosition() とすればよい。また本節中でも述べたが、任意軸周りの回転行列は TH3DMath.GetRotation4x4(deg, axis) によって取得できる (deg にはラジアンではなく度数法による角度を指定し、axis には回転軸を指定する)。
(解答例のプログラムは Sec311_Ans.txt を参照)
# Code5
下左図の2つのベクトル $V_1$、$V_2$ は同じ大きさのベクトルである。この図から明らかなように $V_1$、$V_2$ のなす角は $0^\circ$ でも $180^\circ$ でもない。

ここでの課題は図27のベクトル $V_1$ に適当な回転行列を実行し、$V_2$ に一致させることである。ただし回転行列を求める際には角度を算出する逆関数(Acos や Asin など)を使わないものとする (また $V_1$ と $V_2$ の中間ベクトルを回転軸とする $180^\circ$ 回転もここでは対象外とする)。
プログラムには以下の定数が用意されている。
u1, u2
: 上図27の $V_1$、$V_2$ の方向を表す単位ベクトル (Vector3型)。プログラムはCode5に作成するものとし、$V_1$ の回転は S キーが押された際に行われるものとする。
[Code5] (実行結果 図28)
if (Input.GetKeyDown(KeyCode.S))
{
Vector4 c1 = new Vector4(a, b, c, 0); // 1列目
Vector4 c2 = new Vector4(d, e, f, 0); // 2列目
Vector4 c3 = new Vector4(g, h, i, 0); // 3列目
Vector4 c4 = new Vector4(0, 0, 0, 1); // 4列目
Matrix4x4 R = new Matrix4x4(c1, c2, c3, c4);
RotateV1(R);
}
if (Input.GetKeyDown(KeyCode.C))
{
Reset();
}
今回は自前で回転行列を作成する必要がある。冒頭でも述べたが Matrix4x4 型のインスタンスをコンストラクタ経由で作る場合は $4\times 4$ 行列の各列を引数にセットする (行ではない)。各列を c1、c2、c3、c4 とすれば new Matrix(c1, c2, c3, c4) とすればよい (c1~c4 は Vector4型)。
今回は平行移動は必要ないので第4列目は $(0, 0, 0, 1)$ のままでよい。したがって上のプログラムにおける4~6行目の a、b、c、d、e、f、g、h、i を適当に書き換えて目的の行列を作ることが今回の課題である。
適切な回転行列が10行目の RotateV1(..) にセットされれば、$V_1$ を $V_2$ に一致させる回転が行われ図28のような結果になる (C キーが押されると回転前の状態に戻る)。
今回の課題では角度を使うことができない。しかしベクトルの内積によって $\cos$ が、外積によって $\sin$ がわかるので自ずと答えは出るであろう。もし読者がこの制限でも余裕であれば、さらに平方根を使わないという制限を追加するとよい (この場合 magnitude や normalized のようなプロパティも使うことはできない)。問題としてはそちらの方が面白いはずである。
(解答例のプログラムは Sec311_Ans.txt を参照)。
© 2020-2025 Redpoll's 60 (All rights reserved)