Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-22
第3章 3D空間の基礎
$§$3-22 課題 3
本節及び次節の課題は単一のオブジェクトの運動に関するものである。
ここでは球体の回転移動について扱う。
以下では便宜上 $P_0$~$P_1$ を「第1区間」、$P_1$~$P_2$ を「第2区間」と呼ぶことにする。図に示されるように第1区間、第2区間はいずれも距離は $20$ である。また、この道の中央には白い線が引かれているがこの白い線を「センターライン」と呼ぶことにする。
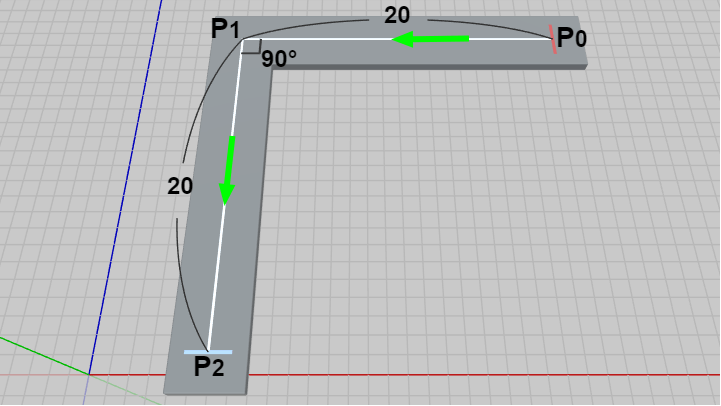
図1 P0~P1が第1区間、P1~P2が第2区間。いずれも距離は 20。
センターライン上には緑の矢印が表示されているが、これは各区間における進行方向を表し、ここでは 第1区間における進行方向は x軸マイナス方向、第2区間における進行方向は z軸マイナス方向である。
下図2はこのプログラムで使用する球体オブジェクトであり、ここでは単に「ボール」と呼ぶことにする。このボールは半径 $1$、初期状態においてその中心が原点に置かれており、球面上に赤いラインと青いラインが引かれている。図3はこのボールをスタート地点 $P_0$ に置いたときのものであるが、ボールには平行移動だけが行われているのでその向きは初期状態と同じである。
図4は $P_0$ に置かれたボールを真上から見下ろしたときのものであり、ボールの赤いラインと第1区間のセンターラインが重なった状態になっている。
ここでの課題は上記のボールをスタート地点 $P_0$ から ゴール地点 $P_2$ までセンターラインに沿って転がしていくことであるが、ボールを転がす際には以下の条件に従うものとする。
「(真上から見下ろしたときに)第1区間においてはボールの赤いラインとセンターラインが重なった状態で移動し、第2区間においてはボールの青いラインとセンターラインが重なった状態で移動する」
つまり 第1区間ではボールを下図5のように移動させ、第2区間ではボールを下図6のように移動させるということである。
スタート地点 $P_0$ においては、すでにボールの赤いラインとセンターラインは重なった状態なので第1区間は問題はないが、第2区間においては青いラインとセンターラインを重なった状態しなければならない。しかし、これについても考える必要はない。
$P_0$ を出発して中間地点 $P_1$ に到着した時点で、上図7に示されるようにボールの青いラインが第2区間のセンターライン上にちょうど来るためである (もちろん $P_0$~$P_1$ の移動中にボールがすべるといったことが起こらないものとする)。
なお上のアニメーションでも見られるように、ボールの赤いライン、青いラインには矢印が付けられているが、この矢印はボールの回転方向を表すものである。ボールがスタート地点に置かれた状態(図4)ではこの矢印は進行方向を向いている。そしてボールを正しく転がしていけばこの矢印は常に進行方向を向いた状態で回転する。
プログラム中ではボールは Ball という変数名で用意されている。この他にプログラムでは以下の2つの定数が用意されている。
そして今回のプログラムではそれ以外に必要なインスタンス変数などについては読者の側で用意するものとする。
プログラムの作成はCode1に行うものとする。Code1は最初の段階では以下のコードのみが記述されている。
[Code1]
このボールは半径が $1$ で初期状態ではその中心が原点に置かれているので、ボールを $P_0$ に置くためには、ボールの中心が $P_0$ から y軸方向に $1$ だけ上に来るように置けばよい。初期化ブロックではその処理だけが記述されている。
またボールの回転移動は S キーが押されたときに始まるものとする (オブジェクトの回転移動については 3-13節 Code6 を参照)。
XZ平面上に下図に示されるような道が置かれている (この道も高さ方向に変化のない平坦な道である)。ここでもスタート地点は $P_0$、中間地点が $P_1$、ゴール地点が $P_2$ であり、先程と同じく $P_0$~$P_1$ を「第1区間」、$P_1$~$P_2$ を「第2区間」と呼ぶことにする。図に示されるように第1区間、第2区間の距離は今回も $20$ である。
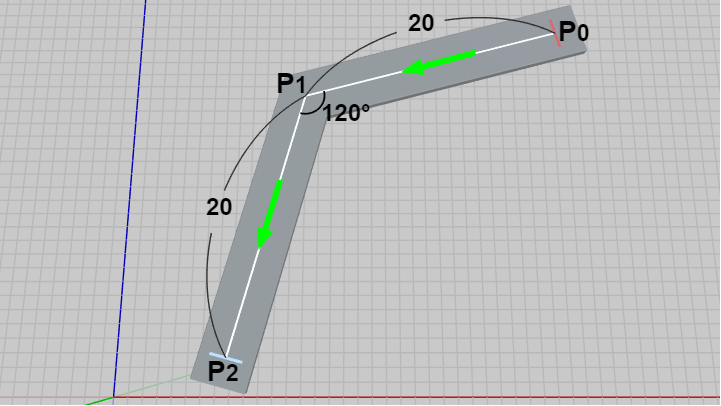
図8 P0~P1が第1区間、P1~P2が第2区間。いずれも距離は 20。
図中の緑の矢印はここでも各区間における進行方向を表すが、今回は第1区間は x軸プラス方向と $15^\circ$ の角をなしており (図9)、第1区間と第2区間のなす角は $120^\circ$ である (図10)。
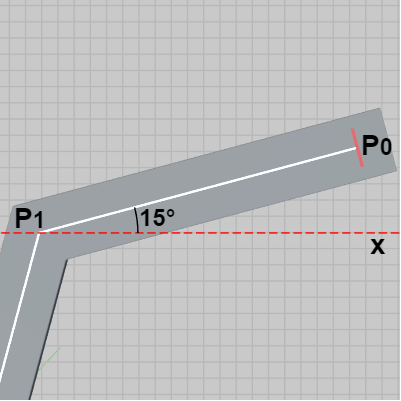
図9 第1区間は x軸プラス方向と 15° の角をなす (図中の点線は x軸に平行)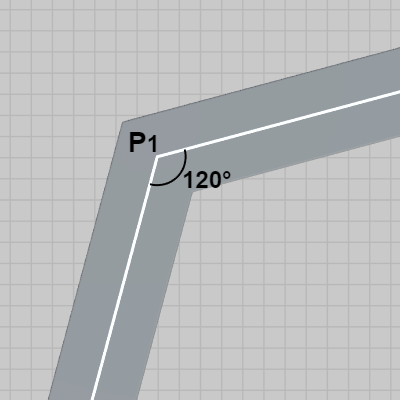 
図10 第1区間と第2区間のなす角は 120°
下図11は今回使用するボールであり、半径は $1$ で初期状態では中心が原点に置かれている。このボールも球面上に赤いラインと青いラインが引かれているが、ボール自体はCode1のボールとは異なるものである。ボールの各ライン上には矢印が付いているが、この矢印はCode1と同じくボールの回転方向を表すものであり、初期状態においては赤いライン上の矢印は x軸マイナス方向を向いている。
図12はこのボールをスタート地点 $P_0$ に置いたときのものであり、ここではボールに対して平行移動だけでなく回転も行われている。具体的にはボールに対してまず y軸周りに $-15^\circ$ の回転を行い、その後に $P_0$ に置かれるように平行移動を行ったときの結果である。
図13は $P_0$ に置かれたボールを真上から見下ろしたときのものであり、ボールの赤いラインと第1区間のセンターラインが重なった状態になっている (ボールの回転方向を表す赤いライン上の矢印は進行方向を向いた状態になっている)。
ここでの課題もスタート地点 $P_0$ からゴール地点 $P_2$ までこのボールをセンターラインに沿って転がしていくことである。そしてCode1と同じく転がしていく際には、(真上から見下ろしたときに)第1区間ではボールの赤いラインとセンターラインが重なった状態で、第2区間ではボールの青いラインとセンターラインが重なった状態で転がしていくものとする。
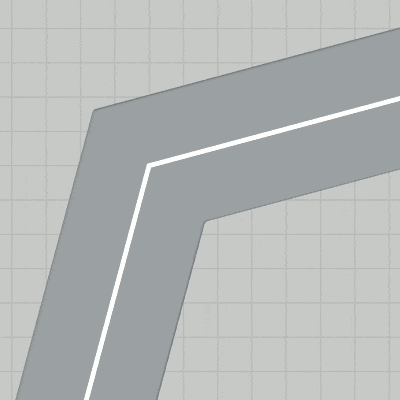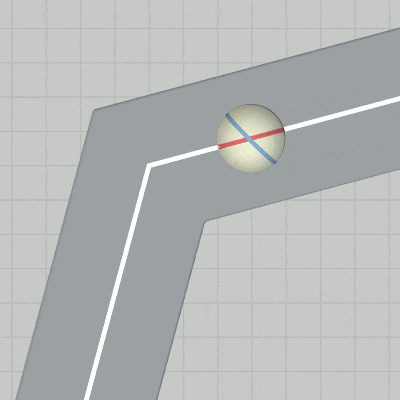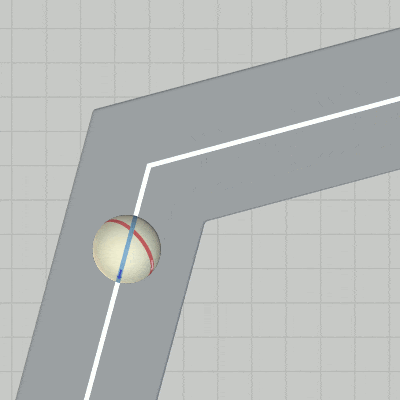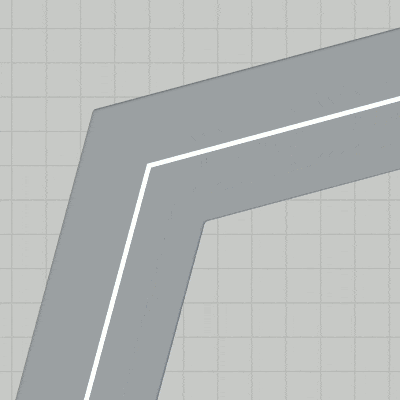
図14 中間地点 P1 における進路変更 第1区間において赤いラインとセンターラインが重なった状態にするためには、上で述べたようにまず y軸周りに $-15^\circ$ 回転させてからスタート地点に移動させればよい。
第2区間において青いラインとセンターラインが重なった状態にすることについては、今回も特に考える必要はない。ボールが $P_0$ を出発してから中間地点 $P_1$ に到着した時点で、右図に示されるように青いラインが第2区間のセンターライン上にちょうど来るためである。
今回のプログラムにおいても用意されているのは2つの定数 P0 (スタート地点)、c_Circumference (ボールの大円の周長) のみである。したがって必要なインスタンス変数などは読者の側で用意しなければならない。
プログラムの作成はCode2に行うものとする。Code2は最初の段階では以下のコードのみが記述されている。
[Code2]
このまま実行するとスタート地点に置かれたボール(図12)が表示される。また今回もボールの回転移動は S キーが押されたときに始まるものとする。
(解答例については Sec322_Ans.txt Code1 及び Code2 を参照)
ここでは球体の回転移動について扱う。
# Code1
XZ平面上に下図に示されるような道が置かれている。この道のスタート地点は $P_0$、中間地点が $P_1$、ゴール地点が $P_2$ で、中間地点 $P_1$ において進行方向が $90^\circ$ 変化している (この道は高さ方向に変化のない平坦な道である。つまり $P_0$、$P_1$、$P_2$ の y座標は同じである)。以下では便宜上 $P_0$~$P_1$ を「第1区間」、$P_1$~$P_2$ を「第2区間」と呼ぶことにする。図に示されるように第1区間、第2区間はいずれも距離は $20$ である。また、この道の中央には白い線が引かれているがこの白い線を「センターライン」と呼ぶことにする。
センターライン上には緑の矢印が表示されているが、これは各区間における進行方向を表し、ここでは 第1区間における進行方向は x軸マイナス方向、第2区間における進行方向は z軸マイナス方向である。
下図2はこのプログラムで使用する球体オブジェクトであり、ここでは単に「ボール」と呼ぶことにする。このボールは半径 $1$、初期状態においてその中心が原点に置かれており、球面上に赤いラインと青いラインが引かれている。図3はこのボールをスタート地点 $P_0$ に置いたときのものであるが、ボールには平行移動だけが行われているのでその向きは初期状態と同じである。
図4は $P_0$ に置かれたボールを真上から見下ろしたときのものであり、ボールの赤いラインと第1区間のセンターラインが重なった状態になっている。
-
図2 Code1のボール 初期状態 (ボールの半径は 1) -
図3 P0に置かれたボール (平行移動だけが行われた状態) -
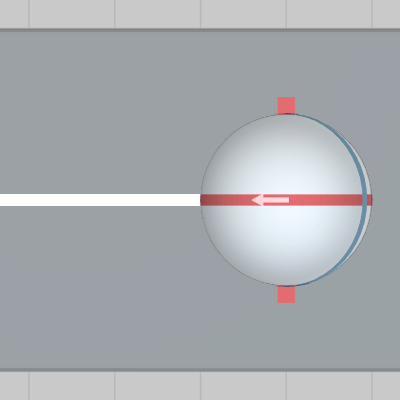図4 真上から見下ろしたとき (ボールの赤いラインと第1区間のセンターラインが重なっている)
ここでの課題は上記のボールをスタート地点 $P_0$ から ゴール地点 $P_2$ までセンターラインに沿って転がしていくことであるが、ボールを転がす際には以下の条件に従うものとする。
「(真上から見下ろしたときに)第1区間においてはボールの赤いラインとセンターラインが重なった状態で移動し、第2区間においてはボールの青いラインとセンターラインが重なった状態で移動する」
つまり 第1区間ではボールを下図5のように移動させ、第2区間ではボールを下図6のように移動させるということである。
-
図5 第1区間における移動 -
図6 第2区間における移動 -
図7 中間地点 P1 における進路変更
スタート地点 $P_0$ においては、すでにボールの赤いラインとセンターラインは重なった状態なので第1区間は問題はないが、第2区間においては青いラインとセンターラインを重なった状態しなければならない。しかし、これについても考える必要はない。
$P_0$ を出発して中間地点 $P_1$ に到着した時点で、上図7に示されるようにボールの青いラインが第2区間のセンターライン上にちょうど来るためである (もちろん $P_0$~$P_1$ の移動中にボールがすべるといったことが起こらないものとする)。
なお上のアニメーションでも見られるように、ボールの赤いライン、青いラインには矢印が付けられているが、この矢印はボールの回転方向を表すものである。ボールがスタート地点に置かれた状態(図4)ではこの矢印は進行方向を向いている。そしてボールを正しく転がしていけばこの矢印は常に進行方向を向いた状態で回転する。
プログラム中ではボールは Ball という変数名で用意されている。この他にプログラムでは以下の2つの定数が用意されている。
P0
: 上記のスタート地点 $P_0$ (Vector3型)。c_Circumference
: ボールの大円の周長 (球面上の赤いライン、青いラインの周長)。上記のボールの半径は $1$ なのでこの定数の値は $2\pi$ である (float型)。プログラムの作成はCode1に行うものとする。Code1は最初の段階では以下のコードのみが記述されている。
[Code1]
if (!i_INITIALIZED)
{
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(P0 + Vector3.up);
Ball.SetMatrix(mtx);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
}
このボールは半径が $1$ で初期状態ではその中心が原点に置かれているので、ボールを $P_0$ に置くためには、ボールの中心が $P_0$ から y軸方向に $1$ だけ上に来るように置けばよい。初期化ブロックではその処理だけが記述されている。
またボールの回転移動は S キーが押されたときに始まるものとする (オブジェクトの回転移動については 3-13節 Code6 を参照)。
# Code2
今回も行うことは同じであるが、多少設定を変更する。XZ平面上に下図に示されるような道が置かれている (この道も高さ方向に変化のない平坦な道である)。ここでもスタート地点は $P_0$、中間地点が $P_1$、ゴール地点が $P_2$ であり、先程と同じく $P_0$~$P_1$ を「第1区間」、$P_1$~$P_2$ を「第2区間」と呼ぶことにする。図に示されるように第1区間、第2区間の距離は今回も $20$ である。
図中の緑の矢印はここでも各区間における進行方向を表すが、今回は第1区間は x軸プラス方向と $15^\circ$ の角をなしており (図9)、第1区間と第2区間のなす角は $120^\circ$ である (図10)。
下図11は今回使用するボールであり、半径は $1$ で初期状態では中心が原点に置かれている。このボールも球面上に赤いラインと青いラインが引かれているが、ボール自体はCode1のボールとは異なるものである。ボールの各ライン上には矢印が付いているが、この矢印はCode1と同じくボールの回転方向を表すものであり、初期状態においては赤いライン上の矢印は x軸マイナス方向を向いている。
図12はこのボールをスタート地点 $P_0$ に置いたときのものであり、ここではボールに対して平行移動だけでなく回転も行われている。具体的にはボールに対してまず y軸周りに $-15^\circ$ の回転を行い、その後に $P_0$ に置かれるように平行移動を行ったときの結果である。
図13は $P_0$ に置かれたボールを真上から見下ろしたときのものであり、ボールの赤いラインと第1区間のセンターラインが重なった状態になっている (ボールの回転方向を表す赤いライン上の矢印は進行方向を向いた状態になっている)。
-
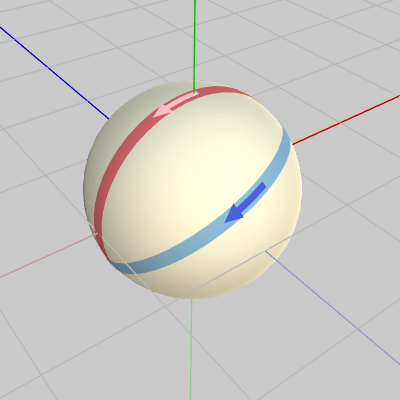図11 Code2のボール 初期状態 (半径は 1) -
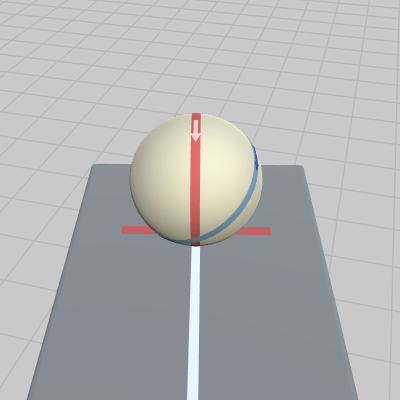図12 P0に置かれたボール (回転と平行移動が行われた状態) -
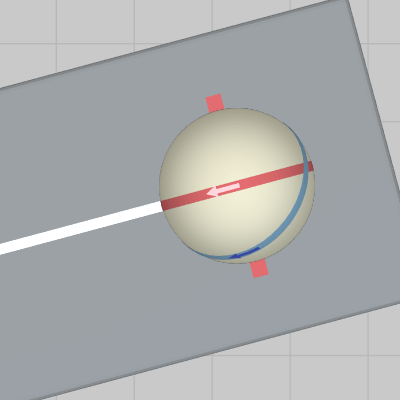図13 真上から見下ろしたとき (ボールの赤いラインと第1区間のセンターラインが重なっている)
ここでの課題もスタート地点 $P_0$ からゴール地点 $P_2$ までこのボールをセンターラインに沿って転がしていくことである。そしてCode1と同じく転がしていく際には、(真上から見下ろしたときに)第1区間ではボールの赤いラインとセンターラインが重なった状態で、第2区間ではボールの青いラインとセンターラインが重なった状態で転がしていくものとする。
第2区間において青いラインとセンターラインが重なった状態にすることについては、今回も特に考える必要はない。ボールが $P_0$ を出発してから中間地点 $P_1$ に到着した時点で、右図に示されるように青いラインが第2区間のセンターライン上にちょうど来るためである。
今回のプログラムにおいても用意されているのは2つの定数 P0 (スタート地点)、c_Circumference (ボールの大円の周長) のみである。したがって必要なインスタンス変数などは読者の側で用意しなければならない。
プログラムの作成はCode2に行うものとする。Code2は最初の段階では以下のコードのみが記述されている。
[Code2]
if (!i_INITIALIZED)
{
Matrix4x4 mtx = TH3DMath.GetTranslation4x4(P0 + Vector3.up) *
TH3DMath.GetRotation4x4(-15.0f, Vector3.up);
Ball.SetMatrix(mtx);
i_INITIALIZED = true;
}
if (Input.GetKeyDown(KeyCode.S))
{
}
このまま実行するとスタート地点に置かれたボール(図12)が表示される。また今回もボールの回転移動は S キーが押されたときに始まるものとする。
(解答例については Sec322_Ans.txt Code1 及び Code2 を参照)
© 2020-2024 Redpoll's 60 (All rights reserved)