Redpoll's 60
Home / 3Dプログラミング入門 / 第3章 $§$3-21
第3章 3D空間の基礎
$§$3-21 課題 2
今までのプログラムにおいて表示されていた座標系(x軸、y軸、z軸を持つ座標系)をコンピューターグラフィックスではワールド座標系 (World Coordinate System)と呼ぶ (ワールド座標系の詳細については第4章で扱う)。
例えば 下図1ではワールド座標系に4つのオブジェクトが置かれており、図2にはそのうちの立方体オブジェクト Box の位置が表示されている。具体的には Box(の中心)のワールド座標は $(7.3,\ 10.1,\ 15.9)$ であるが、これはBox(の中心)がワールド座標系の原点から x軸方向に $7.3$、y軸方向に $10.1$、z軸方向に $15.9$ だけ離れた位置にあることを意味する。

図1 ワールド座標系に置かれた4つのオブジェクト 
図12 Boxのワールド座標
UnityのC# APIを用いてオブジェクトの位置を取得する際には transform.position あるいは transform.localPosition といったプロパティを使用するが、このうちで transform.position にはオブジェクトのワールド座標がセットされている。したがって 上記のBoxの場合とすれば、Boxのワールド座標を取得することができ、ここではその値は $(7.3,\ 10.1,\ 15.9)$ である (transform.position と transform.localPosition の違いについては5-2節参照)。
図3はここで使用するカメラであるが、カメラの前方には3つの軸と白いグリッド線が表示されている。この3つの軸と白いグリッド線はカメラの位置(より正確にはカメラレンズの位置)を原点とする座標系であり、ここではこの座標系のことをカメラ座標系と呼ぶことにする。また 赤、緑、青の3つの軸はそれぞれカメラ座標系の x軸、y軸、z軸である。

図3 カメラ座標系 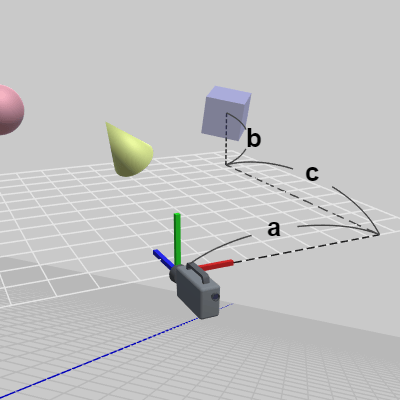
図4
図4はカメラ座標系で測ったときのBoxの位置であり、具体的にはカメラ座標系の x軸方向に $a$、y軸方向に $b$、z軸方向に $c$ だけ離れた位置にBoxの中心が置かれている。したがって その座標は $(a, b, c)$ であるが、この座標はカメラ座標系での座標である。
先程述べたように transform.position はワールド座標を取得することができるのでBoxのワールド座標であれば Box.transform.position とすればよいが、このプロパティが表す内容はワールド座標 $(7.3,\ 10.1,\ 15.9)$ である。つまり transform.position ではBoxのワールド座標を取得することはできるが、カメラ座標系における座標 $(a, b, c)$ を取得することはできないのである。
ではここで、カメラ座標系におけるオブジェクトの座標をどうやって求めるかという問題が生じてくるが、それは例えば次のように考えればよい。

図5
上のアニメーションではカメラ及びカメラ座標系に対して変換を実行しているが、変換実行後においてはカメラ座標系とワールド座標系は完全に一致している。さらに、この変換はカメラ(及びその座標系)だけでなく全てのオブジェクトに対しても同じ変換が行われている。つまり カメラ座標系とワールド座標系を完全に一致させる変換を、カメラだけでなくシーン内の全てのオブジェクトに対して実行しているのである。
その結果として変換前と変換後においてはカメラとオブジェクトとの相対的な位置関係は変わらない。例えば下左図は変換前のカメラ座標系におけるBoxの位置であり、隣りの図6は変換後のカメラ座標系におけるBoxの位置であるが、どちらの場合でもBoxの位置はカメラ座標系において、カメラ座標系の x軸方向に $a$、y軸方向に $b$、z軸方向に $c$ だけ離れた位置にある、すなわち カメラ座標系における座標は $(a, b, c)$ である。

図4 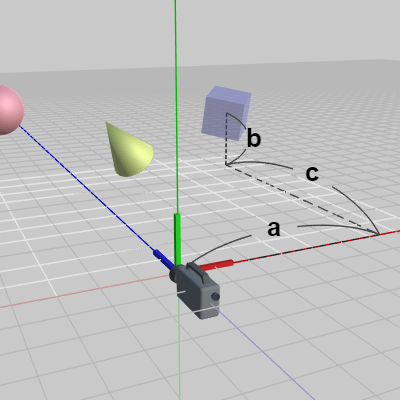
図6
そしてここで重要なのが変換後のカメラ座標系はワールド座標系と完全に一致しているので、Boxの座標はカメラ座標系で測ってもワールド座標系で測っても同じ $(a, b, c)$ であるということである。したがって Box.transform.position で取得される座標はワールド座標ではあるが変換後におけるその値は $(a, b, c)$ であり、これは当初の目的としていたBoxのカメラ座標系での座標である。
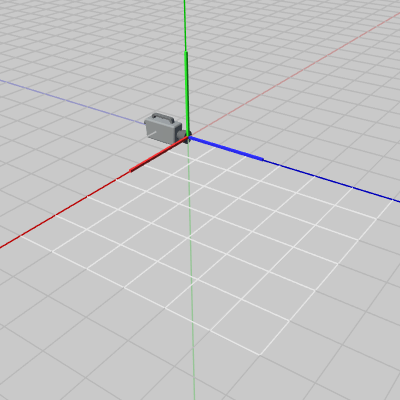
図7 カメラ 初期状態 (初期状態においてはカメラ座標系とワールド座標系が一致している) ここで 1点補足する。
右図7はカメラの初期状態である。カメラは初期状態においては原点に置かれており、その向きは z軸プラス方向を向いている (前節の用語を用いれば「x:right、y:up、z:forward」タイプの左手座標系において、初期状態のカメラは z軸プラス方向を向いている)。そして図に示されるように初期状態ではカメラ座標系とワールド座標系は完全に一致している。
コンピューターグラフィックスにおいては、カメラに実行する変換は一般には平行移動と回転のみである (つまり スケールは使わない)。例えば 上図4ではカメラが適当な位置に置かれ、適当な向きを向いているが、このときのカメラに対して行われている変換も回転と平行移動のみであり、変換もこの順番で行われている。
カメラ座標系におけるオブジェクトの座標を求めるには上のアニメーションに示されるように、カメラを初期状態に戻す変換を行えばよいが、ここではカメラを初期状態に戻す変換行列を $V$ で表すことにする。上図6のカメラは図4のカメラに対して変換行列 $V$ を実行した結果であり、図6のカメラの状態はカメラ座標系とワールド座標系が完全に一致した状態、すなわち初期状態である。
ここでの課題はワールド座標系の適当な位置に適当な方向を向いて置かれているカメラ(図8)に対して変換行列 $V$ を実行し、このカメラを初期状態に戻すことである。具体的には実行結果が図9の状態になればよい。
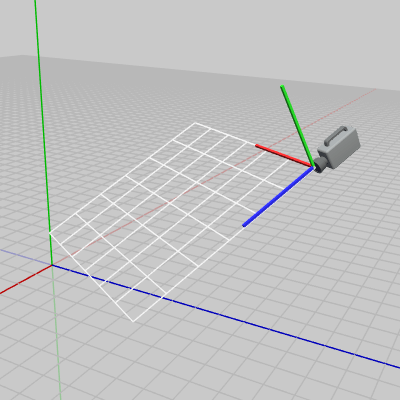
図8 カメラは適当な位置で適当な方向を向いている 
図9 カメラ 初期状態
プログラムはCode1に作成するものとする。Code1は最初の段階では次のコードが記述されている。
[Code1]
プログラム中の MoveCamera(..) は今回用意されているメソッドで、Matrix4x4型のインスタンスを引数にとる。このメソッドは V キーが押された際に、図8のカメラ(及びその座標系)に対して引数にセットされた行列を実行するが、注意すべきはこのメソッドはカメラを図8の状態から変化させるという点である。
今までプログラムで使用してきた SetMatrix(..) はオブジェクトを初期状態から変化させるものであったが、今回の MoveCamera(..) はオブジェクトを図8の状態から変化させるものである。
例えば その引数にセットする変換行列が「x軸方向に $1$ だけの平行移動」を表すものであればカメラが図8の状態から x軸方向に $1$ だけ平行移動する。また 引数にセットする変換行列が「y軸周りに $90^\circ$ の回転」を表すものである場合はカメラが図8の状態から y軸周りに $90^\circ$ 回転する結果になる。
始めの状態では MoveCamera(..) にセットされる変換行列 V の内容はidentity行列であるため、V キーを何度押してもカメラは図8の状態から変化しない。したがってカメラを初期状態に戻すためには8行目の V の内容を適当に書き換える必要があるが、それがここでの課題である。
なお1行目のifブロックは C キーを押した際に入るが、これはカメラを図8の状態に戻す処理が行われる。カメラがどのような状態になっても C キーを押せばカメラは図8の状態に戻る。
プログラムでは以下の2つの定数のみが用意されている。
(解答例については Sec321_Ans.txt を参照 ;
ここで求める変換行列 $V$ を詳しくは View Matrix という)
例えば 下図1ではワールド座標系に4つのオブジェクトが置かれており、図2にはそのうちの立方体オブジェクト Box の位置が表示されている。具体的には Box(の中心)のワールド座標は $(7.3,\ 10.1,\ 15.9)$ であるが、これはBox(の中心)がワールド座標系の原点から x軸方向に $7.3$、y軸方向に $10.1$、z軸方向に $15.9$ だけ離れた位置にあることを意味する。


UnityのC# APIを用いてオブジェクトの位置を取得する際には transform.position あるいは transform.localPosition といったプロパティを使用するが、このうちで transform.position にはオブジェクトのワールド座標がセットされている。したがって 上記のBoxの場合
Vector3 pos = Box.transform.position;
図3はここで使用するカメラであるが、カメラの前方には3つの軸と白いグリッド線が表示されている。この3つの軸と白いグリッド線はカメラの位置(より正確にはカメラレンズの位置)を原点とする座標系であり、ここではこの座標系のことをカメラ座標系と呼ぶことにする。また 赤、緑、青の3つの軸はそれぞれカメラ座標系の x軸、y軸、z軸である。


図4はカメラ座標系で測ったときのBoxの位置であり、具体的にはカメラ座標系の x軸方向に $a$、y軸方向に $b$、z軸方向に $c$ だけ離れた位置にBoxの中心が置かれている。したがって その座標は $(a, b, c)$ であるが、この座標はカメラ座標系での座標である。
先程述べたように transform.position はワールド座標を取得することができるのでBoxのワールド座標であれば Box.transform.position とすればよいが、このプロパティが表す内容はワールド座標 $(7.3,\ 10.1,\ 15.9)$ である。つまり transform.position ではBoxのワールド座標を取得することはできるが、カメラ座標系における座標 $(a, b, c)$ を取得することはできないのである。
ではここで、カメラ座標系におけるオブジェクトの座標をどうやって求めるかという問題が生じてくるが、それは例えば次のように考えればよい。

上のアニメーションではカメラ及びカメラ座標系に対して変換を実行しているが、変換実行後においてはカメラ座標系とワールド座標系は完全に一致している。さらに、この変換はカメラ(及びその座標系)だけでなく全てのオブジェクトに対しても同じ変換が行われている。つまり カメラ座標系とワールド座標系を完全に一致させる変換を、カメラだけでなくシーン内の全てのオブジェクトに対して実行しているのである。
その結果として変換前と変換後においてはカメラとオブジェクトとの相対的な位置関係は変わらない。例えば下左図は変換前のカメラ座標系におけるBoxの位置であり、隣りの図6は変換後のカメラ座標系におけるBoxの位置であるが、どちらの場合でもBoxの位置はカメラ座標系において、カメラ座標系の x軸方向に $a$、y軸方向に $b$、z軸方向に $c$ だけ離れた位置にある、すなわち カメラ座標系における座標は $(a, b, c)$ である。


そしてここで重要なのが変換後のカメラ座標系はワールド座標系と完全に一致しているので、Boxの座標はカメラ座標系で測ってもワールド座標系で測っても同じ $(a, b, c)$ であるということである。したがって Box.transform.position で取得される座標はワールド座標ではあるが変換後におけるその値は $(a, b, c)$ であり、これは当初の目的としていたBoxのカメラ座標系での座標である。

右図7はカメラの初期状態である。カメラは初期状態においては原点に置かれており、その向きは z軸プラス方向を向いている (前節の用語を用いれば「x:right、y:up、z:forward」タイプの左手座標系において、初期状態のカメラは z軸プラス方向を向いている)。そして図に示されるように初期状態ではカメラ座標系とワールド座標系は完全に一致している。
コンピューターグラフィックスにおいては、カメラに実行する変換は一般には平行移動と回転のみである (つまり スケールは使わない)。例えば 上図4ではカメラが適当な位置に置かれ、適当な向きを向いているが、このときのカメラに対して行われている変換も回転と平行移動のみであり、変換もこの順番で行われている。
カメラ座標系におけるオブジェクトの座標を求めるには上のアニメーションに示されるように、カメラを初期状態に戻す変換を行えばよいが、ここではカメラを初期状態に戻す変換行列を $V$ で表すことにする。上図6のカメラは図4のカメラに対して変換行列 $V$ を実行した結果であり、図6のカメラの状態はカメラ座標系とワールド座標系が完全に一致した状態、すなわち初期状態である。
ここでの課題はワールド座標系の適当な位置に適当な方向を向いて置かれているカメラ(図8)に対して変換行列 $V$ を実行し、このカメラを初期状態に戻すことである。具体的には実行結果が図9の状態になればよい。


プログラムはCode1に作成するものとする。Code1は最初の段階では次のコードが記述されている。
[Code1]
if (Input.GetKeyDown(KeyCode.C))
{
Reset();
}
if (Input.GetKeyDown(KeyCode.V))
{
Matrix4x4 V = Matrix4x4.identity;
MoveCamera(V);
}
プログラム中の MoveCamera(..) は今回用意されているメソッドで、Matrix4x4型のインスタンスを引数にとる。このメソッドは V キーが押された際に、図8のカメラ(及びその座標系)に対して引数にセットされた行列を実行するが、注意すべきはこのメソッドはカメラを図8の状態から変化させるという点である。
今までプログラムで使用してきた SetMatrix(..) はオブジェクトを初期状態から変化させるものであったが、今回の MoveCamera(..) はオブジェクトを図8の状態から変化させるものである。
例えば その引数にセットする変換行列が「x軸方向に $1$ だけの平行移動」を表すものであればカメラが図8の状態から x軸方向に $1$ だけ平行移動する。また 引数にセットする変換行列が「y軸周りに $90^\circ$ の回転」を表すものである場合はカメラが図8の状態から y軸周りに $90^\circ$ 回転する結果になる。
始めの状態では MoveCamera(..) にセットされる変換行列 V の内容はidentity行列であるため、V キーを何度押してもカメラは図8の状態から変化しない。したがってカメラを初期状態に戻すためには8行目の V の内容を適当に書き換える必要があるが、それがここでの課題である。
なお1行目のifブロックは C キーを押した際に入るが、これはカメラを図8の状態に戻す処理が行われる。カメラがどのような状態になっても C キーを押せばカメラは図8の状態に戻る。
プログラムでは以下の2つの定数のみが用意されている。
T, R
: 図8の状態のカメラに対して実行されている変換は上で述べたように回転と平行移動がこの順序で行われている。$T$、$R$ はその変換を表す行列であり($T$ が平行移動行列、$R$ が回転行列)、カメラに対して実行されている変換行列を $M$ とすれば $M = TR$ である (いずれも Matrix4x4型)。(解答例については Sec321_Ans.txt を参照 ;
ここで求める変換行列 $V$ を詳しくは View Matrix という)
© 2020-2025 Redpoll's 60 (All rights reserved)